Similar presentations:
Производная. Происхождение производной
1. Производная
2. Происхождение производной.
Первую задачу: о связи скорости и пути прямолинейнои неравномерно движущейся точки впервые решил
Ньютон. Он пришел к формуле :
s2 s1
v lim
t 2 t1 t t
2
1
3.
Производной функции у = f(x), заданной нанекотором интервале (a;b), в некоторой
точке х этого интервала называют
предел отношения приращения функции
в этой точке к соответствующему
приращению аргумента, когда
приращение аргумента стремится к
∆f
нулю.
f ′(x) = lim
∆x→0 ∆x
4.
Нахождение производной называютдифференцированием
С 0
x
1
1
2
х
х
1
2 х
x ' nx
n
n 1
x 2х
kx b k
2
5. Таблица производных
f (x)C
kx + b
x2
xn
1/x
sin x
cos x
f ′(x)
0
k
2x
nxn–1
– 1/x2
cos x
– sin x
f (x)
√x
ex
ax
tg x
ctg x
ln x
loga x
f ′(x)
1/(2√x)
ex
ax lna
1/cos2x
– 1/sin2x
1/x
1/(x lna)
6. Правила нахождения производной
1. Если функции u(x) и v(x) имеют в точке хпроизводные, то их сумма u(x) + v(x) также имеет в
этой точке производную, причем
(u + v)′ = u′ + v′
2. Если функция u(x) имеет в точке х производную и С –
данное число, то функция С∙u(x) также имеет в этой
точке производную, причем
(Сu)′ = С∙u′
7. Правила нахождения производной
3. Если функции u(x) и v(x) имеют в точке хпроизводные, то их произведение u(x) ∙ v(x) также
имеет в этой точке производную, причем
(u ∙ v)′ = u′∙v + u∙v′
4. Если функция v(x) имеет в точке х производную и
1
v(x) ≠ 0, то функция
также имеет в этой точке
v(x)
производную, причем
()
v′
1′
=– 2
v
v
8. Правила нахождения производной
5. Если функции u(x) и v(x) имеют в точке хu(x)
производные и v(x) ≠ 0, то функция
также имеет
v(x)
в этой точке производную, причем
( )
u ′
u′v – uv′
v =
v2
6.Производная сложной функции
(f(g(x)))′ = f′(g(x))∙g′(x)
9.
Примеры1) g ( x) x 3x 4
2
Ответ : g ( x) 2 x 3
2) f ( x) 3x 7 x 2 x
3
2
Ответ : f ( x) 12 x 21x 4 x
4
3
2
3) h( x) (2 x 1)
Ответ : h ( x) 4(2 x 1)
2
10.
Примеры4) y sin 2 x
Ответ : y 2 cos 2 x
5) y 3x cosx.
2
Ответ : y 6 x sin x
6) y e (2 x 1).
3x
3x
3x
y (e ) (2 x 1) e (2 x 1)
Ответ :
3x
3x
y 3e (2 x 1) 2e .
11.
ЗАДАЧА №1Тело, подброшенное вверх движется по закону
s(t) = 4+ 8t – 5t 2 . Найдите:
1) Скорость тела в начальный момент времени;
2) Наибольшую высоту подъёма тела.
РЕШЕНИЕ.
1) v (t) = s` (t) = 8 – 10t - скорость
тела;
v(t ) S (t ) 2) t= 0, v(0) = s`(0) = 8 м/с – скорость
тела в начальный момент времени
подсказка
3) s (0,8)= 4+ 8·0,8 – 5· 0,64 =7,2 м –
максимальная высота броска
тела.
Ответ: 8 м/с ; 7,2 м .
12. ЗАДАЧА №2
При каких значениях х значениепроизводной функции f ( x) 2 x3 3x 2 12 x 1
равно 0
3 1
2 1
f
(
x
)
2
3
x
2
3
x
12
f ( x) 2 x 3x 12 x 1
3
2
2
f ( x) 6 x 6 x 12
6 x 6 x 12 0(: 6)
2
f ( x ) 0
x x 2 0
2
D 1 4 1 ( 2) 1 8 9; D 3
x1
1 3
2
2
1 3
x2
1
2
Ответ : x1 2, x2 1
13.
Примерыа) f ( x) x х
2
3
1
б ) f ( x) 5 x 2
х
14.
в) f ( x) x 3 х 12
г) f ( x) x х
3
15.
16.
Найдите производные функций:x 1
2Правильный
x 1
2
x
8
2 Правильный
2x
1
Правильный
2 x ответ
4 cos x
Правильный
4sin x
х
sin
x
Правильный
sin
x x cos x
2
ответ
ответ
ответ
ответ
17.
Найдите производную функции(устно):а) у = 6х5 – 7х3 + 2х2 – 5,
Правильный
/
4 – 21х2 + 4х ,
у = 30 хответ
б) у = (4 – 5х)7,
у/ = 7·(– 5)·(4Правильный
– 5х)6 = – 35·(4 – 5х)6
ответ
в) у = 8 + 3cosх,
Правильный
/
у = 8 – 3sinх
ответ
г) у = 4sinх – 6 lnx,
у/ = 4Правильный
cos х – 6/х
ответ
18. Найдите производную функции(устно):
Правильныйответ
Правильный
ответ
Правильный
ответ
Правильный
ответ
19.
20.
3.4.
5.
21.
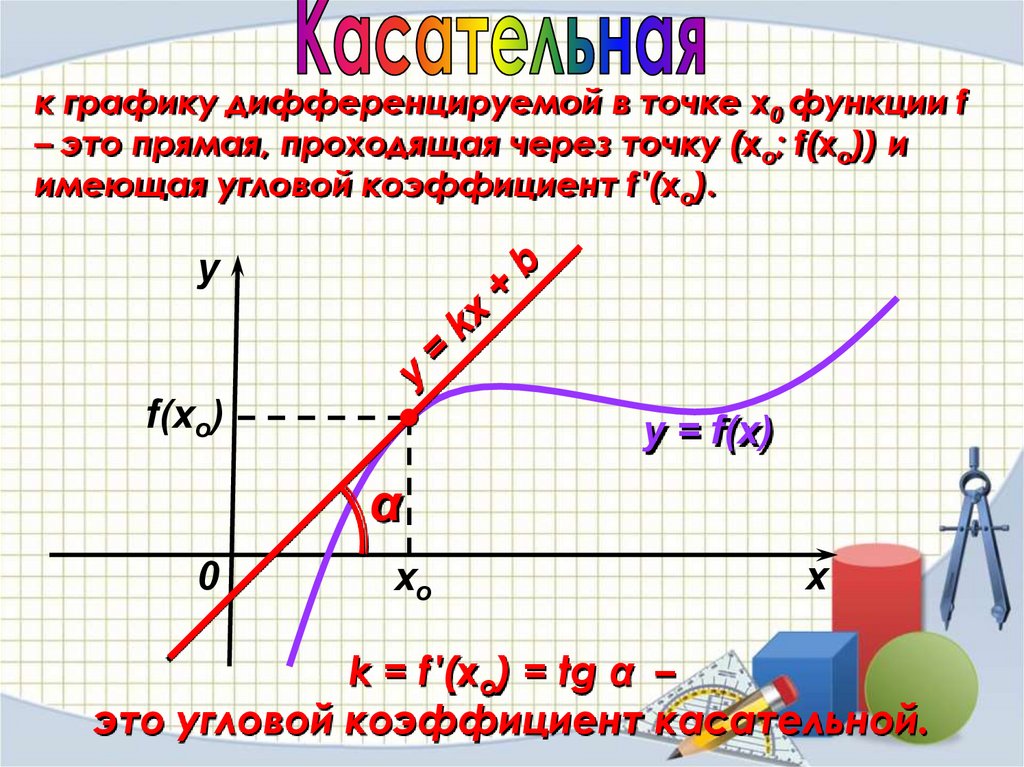
к графику дифференцируемой в точке х0 функции f– это прямая, проходящая через точку (хо; f(xо)) и
имеющая угловой коэффициент f′(хо).
у
f(xo)
y = f(x)
α
0
хо
х
k = f′(xo) = tg α –
это угловой коэффициент касательной.
22.
y = f ′(xo)(x – xo) + f(xo)1о Находим значение функции в точке хо: f(xo).
2о Дифференцируем функцию: f′(x).
3о Находим значение производной в точке хо: f′(xo).
4о Подставляем эти данные в общее уравнения
касательной:
y = f′(xo)(x – xo) + f(xo).
23.
•Одна из основных задач исследованияфункции – это нахождение промежутков её
возрастания и убывания.
Признак возрастания функции:
Если f´(x)>0 в каждой точке интервала
I, то функция f возрастает на I.
Признак убывания функции:
Если f´(x)<0 в каждой точке интервала
I, то функция f убывает на I.
24. Алгоритм решения неравенств методом интервалов:
Выделить функцию y=f(x).1. Найти область определения функции D(f).
Указать промежутки непрерывности.
2. Найти нули функции, решив уравнение
f(x)=0.
3. Определить знак функции между
её нулями в области определения.
25.
Решите неравенство:2x+5≠0, х ≠-2,5
1.
2. f(x)=0, если
x1= 8, x2= -2
3.
-2,5
Ответ:
-2
8
X
26. Алгоритм нахождения промежутков возрастания (убывания) функции y=f(x):
1.Найти производную функции f´(x).2.Решить уравнение f´ (x) =0.
3.Найти знак производной на каждом
интервале.
4.Согласно признаку возрастания
(убывания) функции, найти
промежутки возрастания и
убывания.
27.
Найдите промежутки возрастания и убыванияфункции:
1.
2. f´(x)=0, если
3.
f´(x
)f (x)
Ответ:
0
1
X
28.
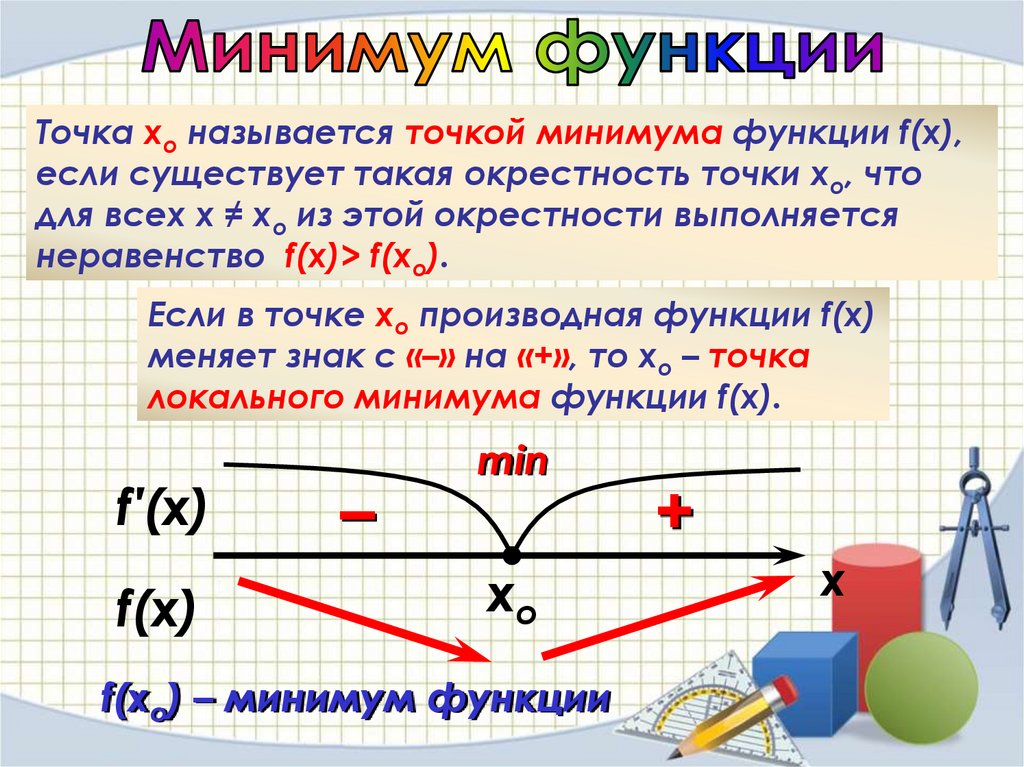
Точка хо называется точкой минимума функции f(x),если существует такая окрестность точки хо, что
для всех х ≠ хо из этой окрестности выполняется
неравенство f(x)> f(xo).
Если в точке хо производная функции f(x)
меняет знак с «–» на «+», то хо – точка
локального минимума функции f(x).
f′(x)
f(x)
–
min
xo
f(xо) – минимум функции
+
x
29.
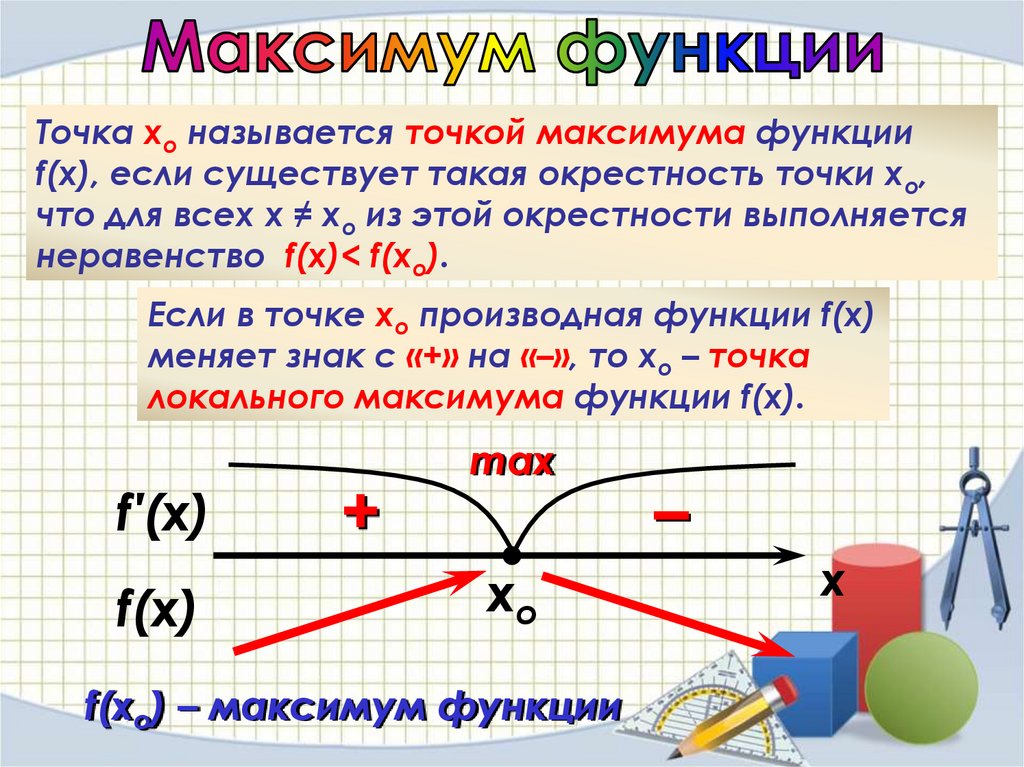
Точка хо называется точкой максимума функцииf(x), если существует такая окрестность точки хо,
что для всех х ≠ хо из этой окрестности выполняется
неравенство f(x)< f(xo).
Если в точке хо производная функции f(x)
меняет знак с «+» на «–», то хо – точка
локального максимума функции f(x).
f′(x)
f(x)
+
max
xo
f(xо) – максимум функции
–
x
30.
1о Дифференцируем функцию: f′(x).2о Находим критические точки из уравнения: f′(x) = 0.
3о Решаем неравенства: f′(x) > 0 и f′(x) < 0.
4о Полученные данные изображаем на схеме:
f′(x)
f(x)
+
–
x1
+
x2
–
x3
5o a) Промежутки возрастания: (– ∞; х1]; [x2; x3].
б) Промежутки убывания: [x1; x2]; [x3; + ∞).
x
31.
1о Дифференцируем функцию: f′(x).2о Находим критические точки из уравнения: f′(x) = 0.
3о Решаем неравенства: f′(x) > 0 и f′(x) < 0.
4о Полученные данные изображаем на схеме:
f′(x)
f(x)
+
–
x1
+
x2
–
x3
5o a) х1; x3 – точки максимума; x2 – точка минимума.
б) f(x1); f(x3) – максимумы функции;
f(x2) – минимум функции.
x
32. Примеры
33.
34.
+–
+ –
+
































 mathematics
mathematics








