Similar presentations:
Выполнение и анализ простых алгоритмов
1.
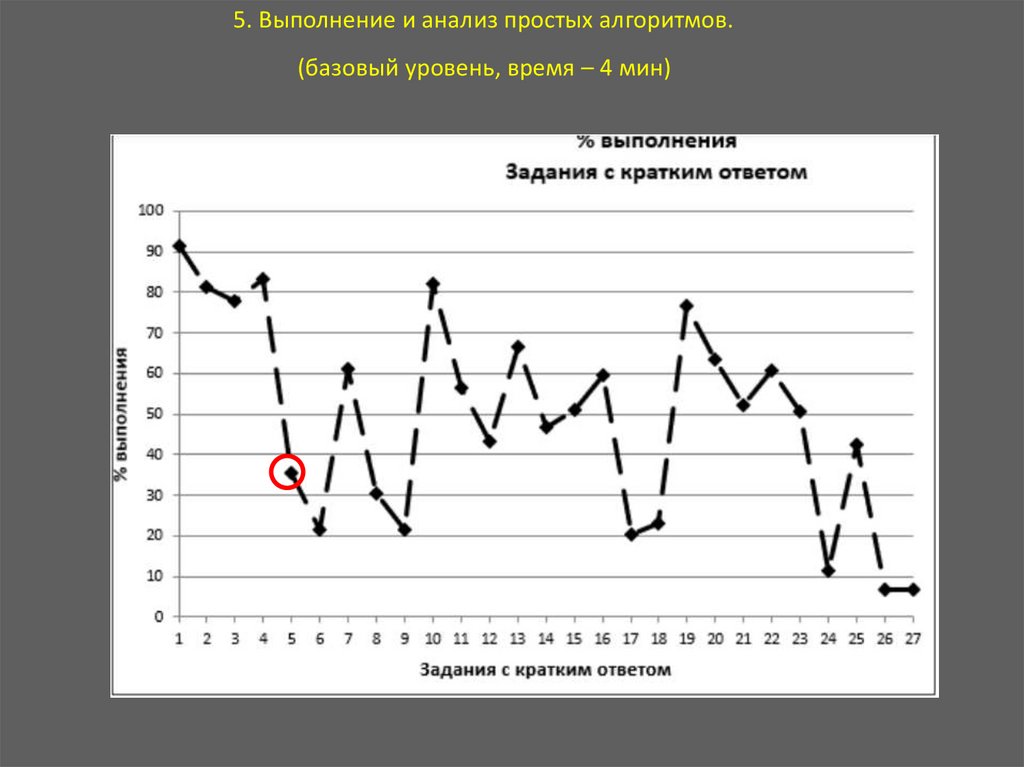
5. Выполнение и анализ простых алгоритмов.(базовый уровень, время – 4 мин)
2.
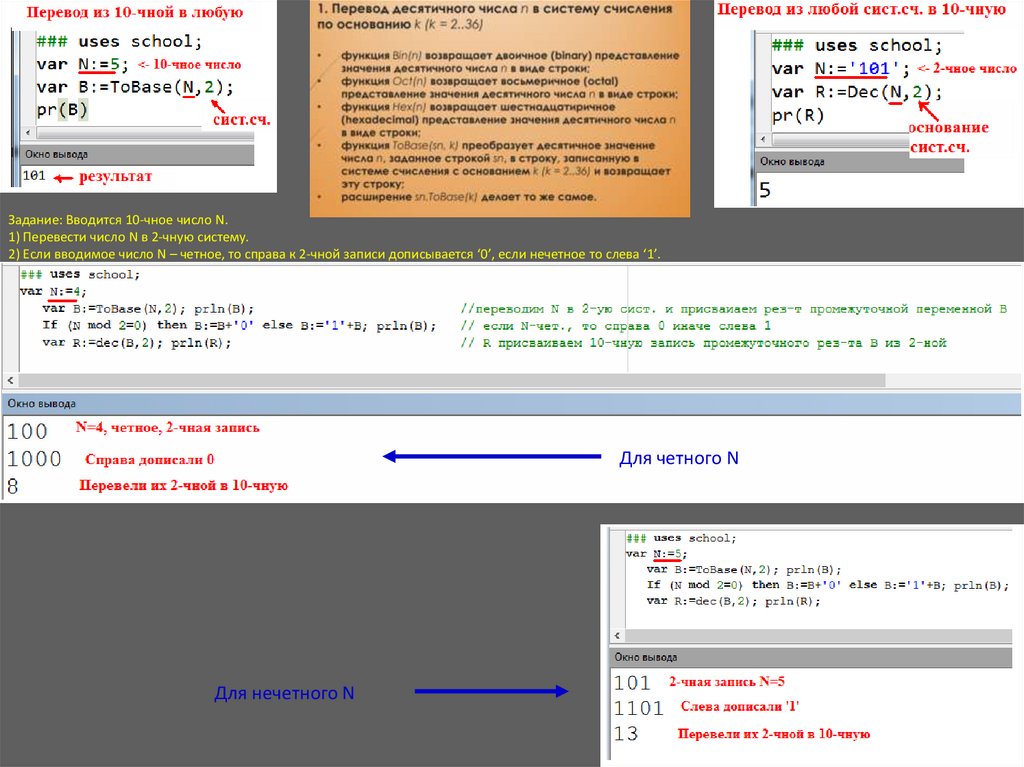
Задание: Вводится 10-чное число N.1) Перевести число N в 2-чную систему.
2) Если вводимое число N – четное, то справа к 2-чной записи дописывается ‘0’, если нечетное то слева ‘1’.
Вывести результат в 10-чной системе счисления.
Для четного N
Для нечетного N
3.
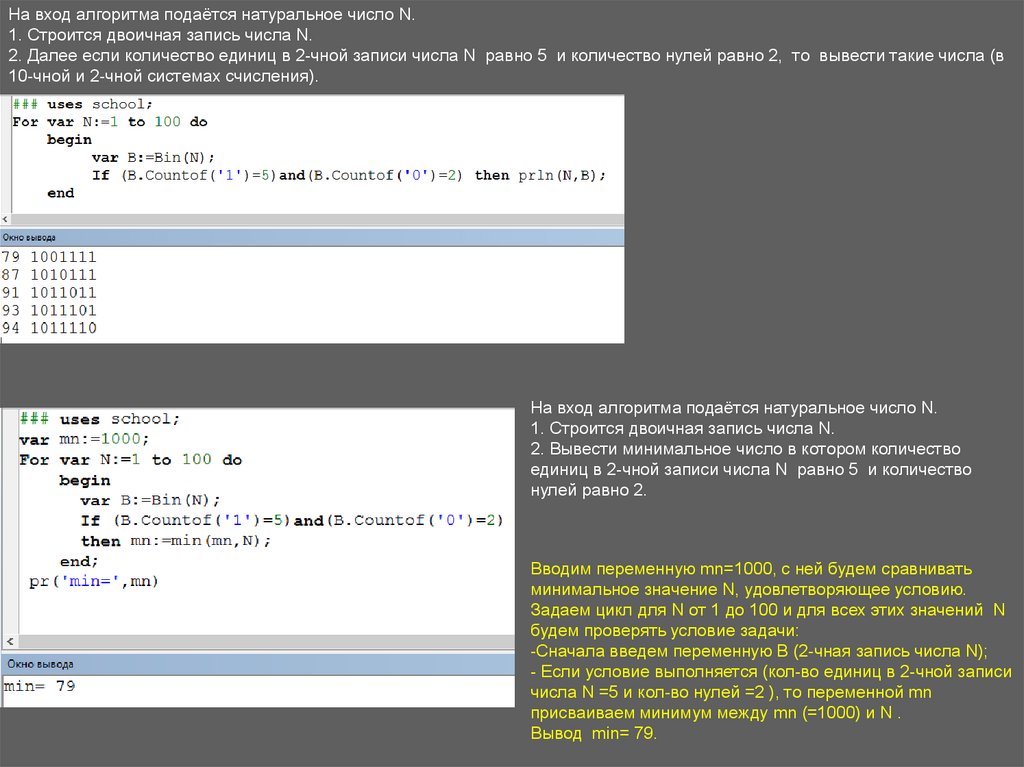
На вход алгоритма подаётся натуральное число N.1. Строится двоичная запись числа N.
2. Далее если количество единиц в 2-чной записи числа N равно 5 и количество нулей равно 2, то вывести такие числа (в
10-чной и 2-чной системах счисления).
На вход алгоритма подаётся натуральное число N.
1. Строится двоичная запись числа N.
2. Вывести минимальное число в котором количество
единиц в 2-чной записи числа N равно 5 и количество
нулей равно 2.
Вводим переменную mn=1000, с ней будем сравнивать
минимальное значение N, удовлетворяющее условию.
Задаем цикл для N от 1 до 100 и для всех этих значений N
будем проверять условие задачи:
-Сначала введем переменную В (2-чная запись числа N);
- Если условие выполняется (кол-во единиц в 2-чной записи
числа N =5 и кол-во нулей =2 ), то переменной mn
присваиваем минимум между mn (=1000) и N .
Вывод min= 79.
4.
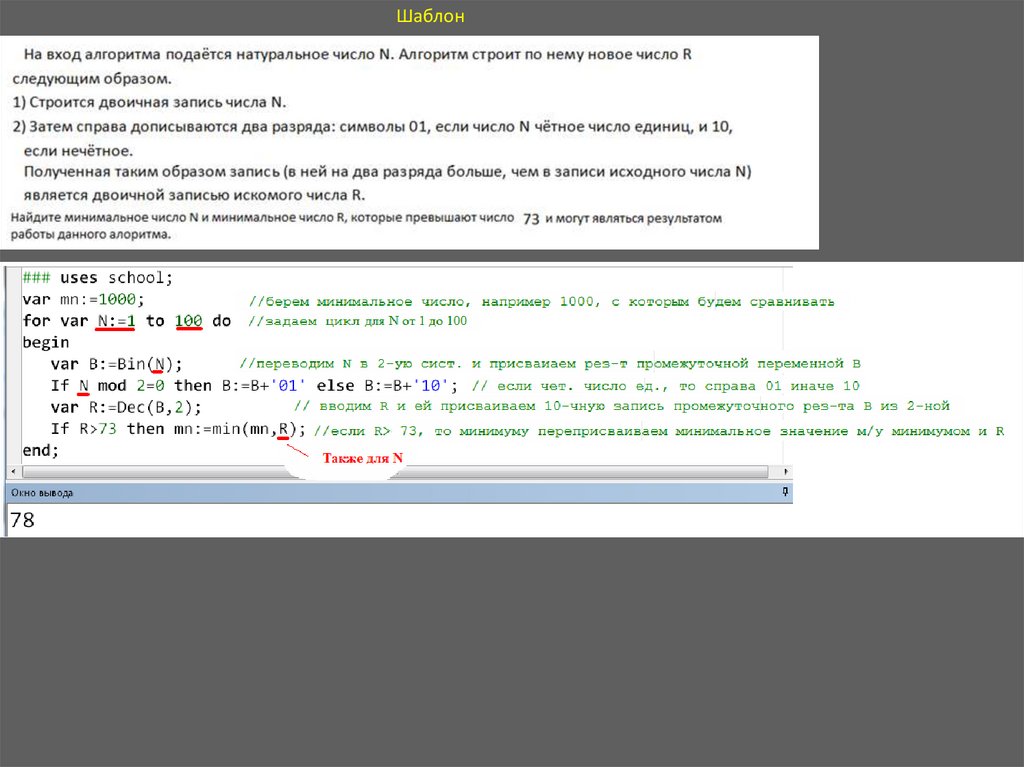
Шаблон5.
Шаблон6.
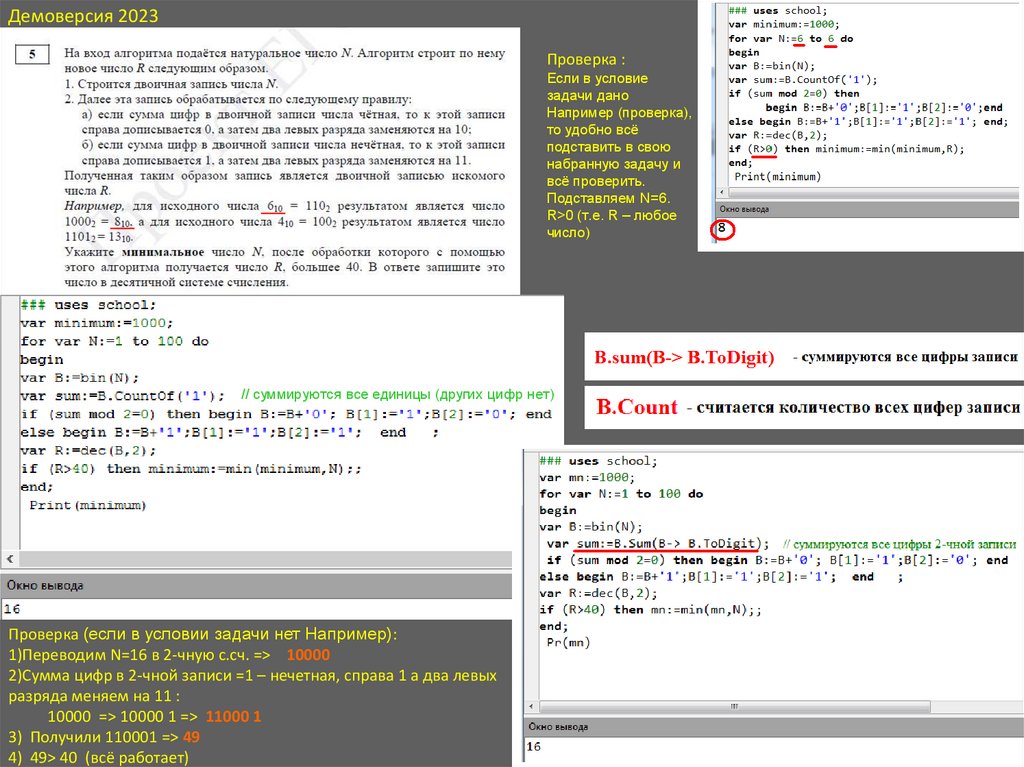
Демоверсия 2023Проверка :
Если в условие
задачи дано
Например (проверка),
то удобно всё
подставить в свою
набранную задачу и
всё проверить.
Подставляем N=6.
R>0 (т.е. R – любое
число)
// суммируются все единицы (других цифр нет)
Проверка (если в условии задачи нет Например):
1)Переводим N=16 в 2-чную с.сч. => 10000
2)Сумма цифр в 2-чной записи =1 – нечетная, справа 1 а два левых
разряда меняем на 11 :
10000 => 10000 1 => 11000 1
3) Получили 110001 => 49
4) 49> 40 (всё работает)
7.
Демо 2024Проверка : (выведем в программе R и N. R=163. N=20)
1)
Переводим N=20 в 2-чную с.сч. =>
10100
2)
N=20 не делится на 3, остаток от
деления 20 на 3 умножаем на 3,
переводим в 2-чную сист.сч. И
дописываем справа:
20 mod 3=2, 2*3=6, 6=> 110,
10100 110
3) Получили R=10100 110 => 166
4) 166> 151 (всё работает)
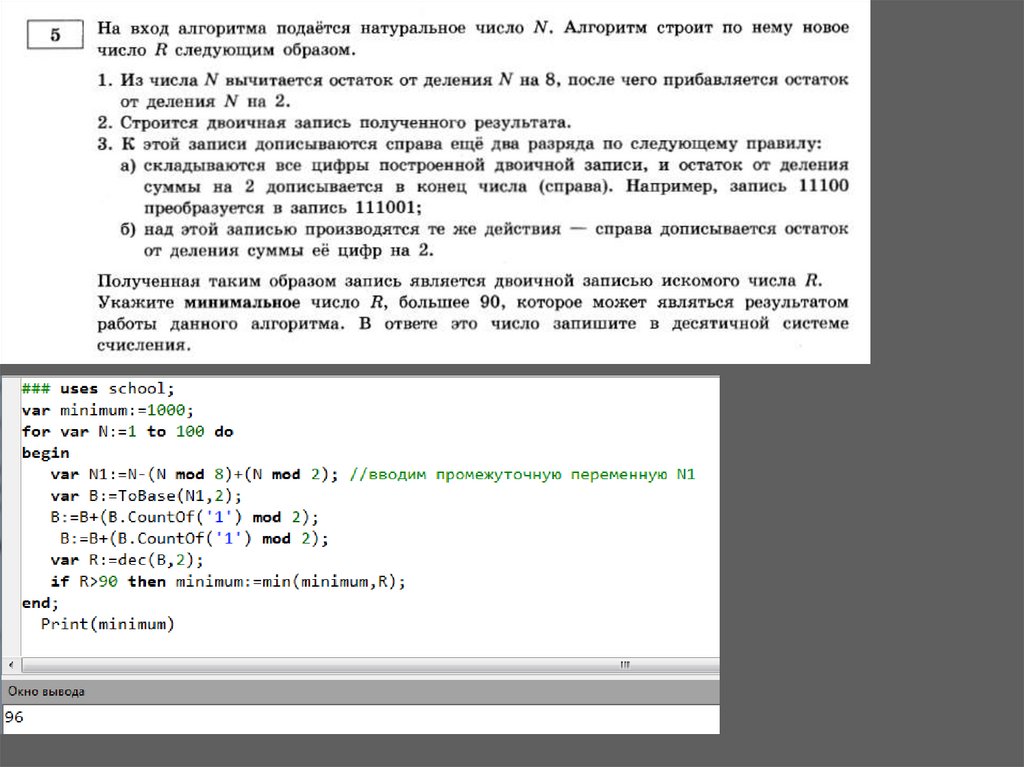
Проверка
N переводится
в 10-чную сист.сч. из 2-чной
Если N кр.3, то к 2-чной
записи N дописывается три
последние цифры.
N в 2-чную сист.сч.
Иначе остаток умножается на 3,
переводится в 2-чную сист. сч.
записи N дописывается три
последние цифры.
8.
9.
10.
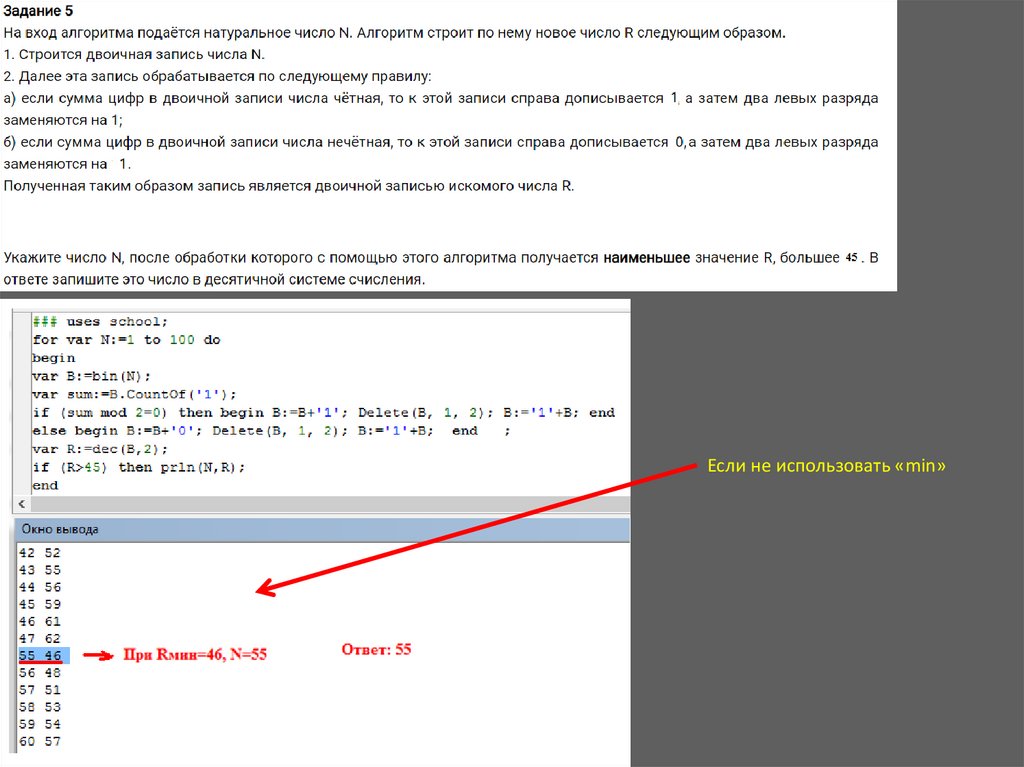
Если не использовать «min»11.
Задание 512.
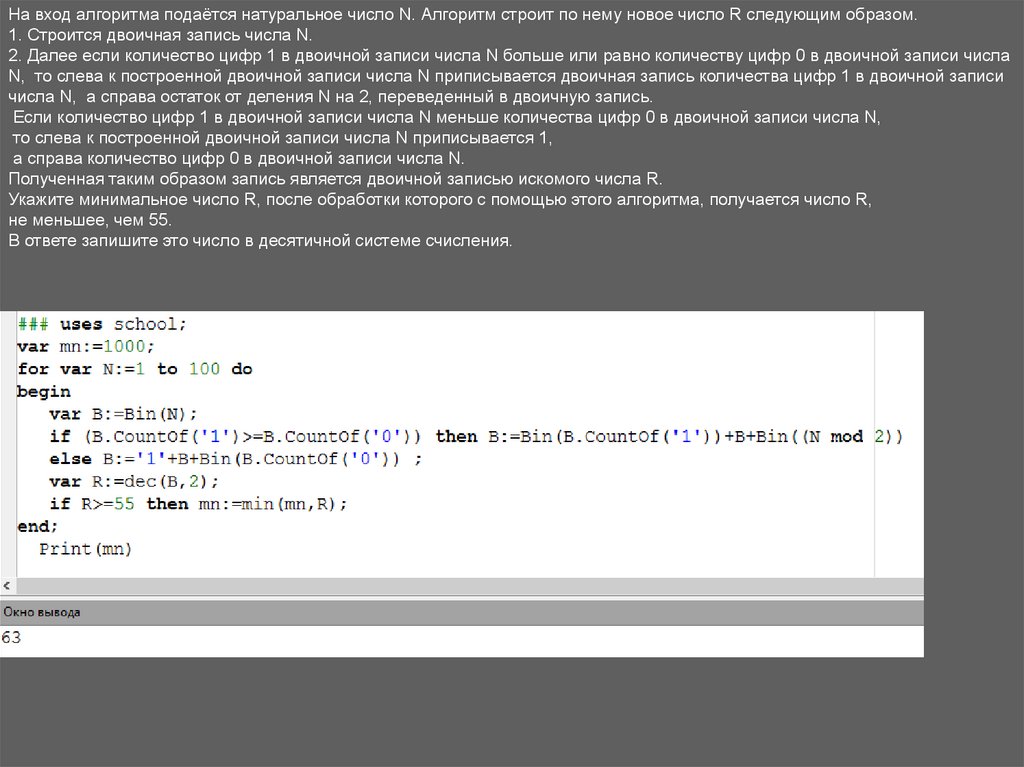
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.1. Строится двоичная запись числа N.
2. Далее если количество цифр 1 в двоичной записи числа N больше или равно количеству цифр 0 в двоичной записи числа
N, то слева к построенной двоичной записи числа N приписывается двоичная запись количества цифр 1 в двоичной записи
числа N, а справа остаток от деления N на 2, переведенный в двоичную запись.
Если количество цифр 1 в двоичной записи числа N меньше количества цифр 0 в двоичной записи числа N,
то слева к построенной двоичной записи числа N приписывается 1,
а справа количество цифр 0 в двоичной записи числа N.
Полученная таким образом запись является двоичной записью искомого числа R.
Укажите минимальное число R, после обработки которого с помощью этого алгоритма, получается число R,
не меньшее, чем 55.
В ответе запишите это число в десятичной системе счисления.
13.
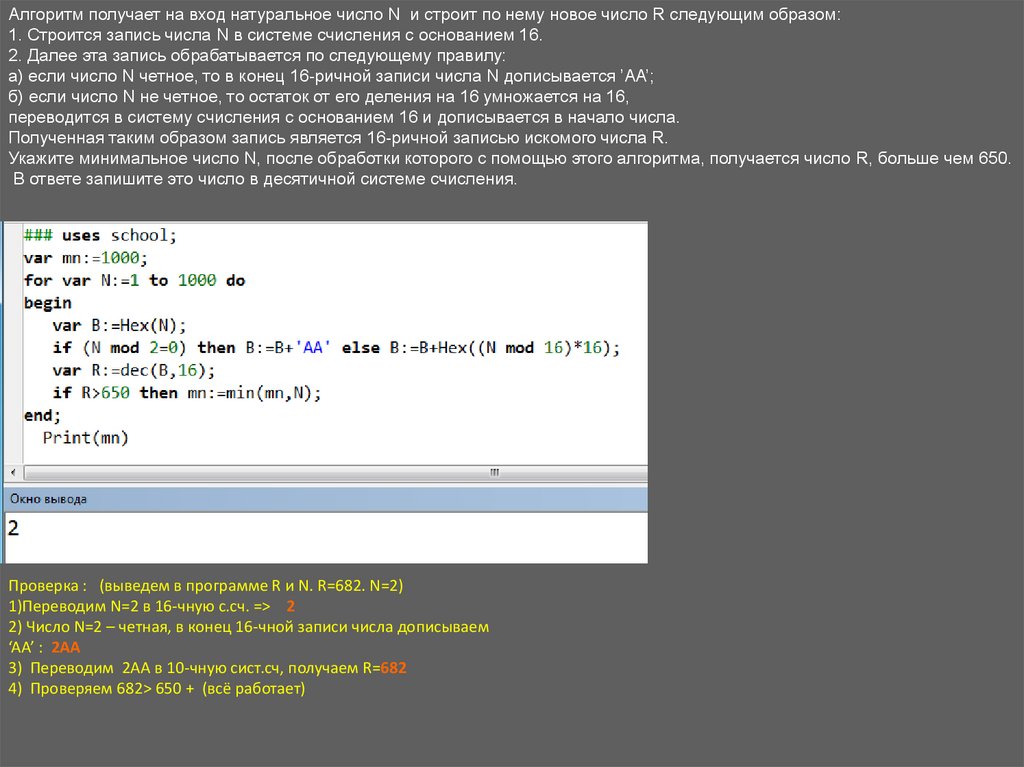
Алгоритм получает на вход натуральное число N и строит по нему новое число R следующим образом:1. Строится запись числа N в системе счисления с основанием 16.
2. Далее эта запись обрабатывается по следующему правилу:
а) если число N четное, то в конец 16-ричной записи числа N дописывается ’AA’;
б) если число N не четное, то остаток от его деления на 16 умножается на 16,
переводится в систему счисления с основанием 16 и дописывается в начало числа.
Полученная таким образом запись является 16-ричной записью искомого числа R.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма, получается число R, больше чем 650.
В ответе запишите это число в десятичной системе счисления.
Проверка : (выведем в программе R и N. R=682. N=2)
1)Переводим N=2 в 16-чную с.сч. => 2
2) Число N=2 – четная, в конец 16-чной записи числа дописываем
‘AA’ : 2AA
3) Переводим 2АА в 10-чную сист.сч, получаем R=682
4) Проверяем 682> 650 + (всё работает)
14.
Алгоритм получает на вход натуральное число N и строит по нему новое число R следующим образом:1. Строится двоичная запись числа N.
2. В конец двоичной записи добавляются две цифры, соответствующие двоичной записи остатка от деления исходного числа
на 3.
3. В конец двоичной записи числа, полученного на предыдущем шаге, добавляются три цифры, соответствующие двоичной
записи остатка от деления этого числа на 5.
4. Результатом работы алгоритма становится десятичная запись полученного числа R.
Пример. Дано число N = 13. Алгоритм работает следующим образом:
1. Строим двоичную запись: 1310 = 11012.
2. Остаток от деления 13 на 3 равен 1, добавляем к двоичной записи цифры 01, получаем 1101012 = 5310.
3. Остаток от деления 53 на 5 равен 3, добавляем к двоичной записи цифры 011, получаем 1101010112 = 42710.
4. Результат работы алгоритма R = 427.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма, получается число R, больше чем 650.
В ответе запишите это число в десятичной системе счисления.




 informatics
informatics








