Приложение производной при исследовании функций и построению графиков. Лекция № 5

1.

Лекция № 5
Приложение производной
при исследовании
функций и построению
графиков.

2.

Содержание

3.

Применение производной к исследованию функции
Признак возрастания и убывания (монотонность)
Достаточный признак возрастания функции. Если >0 в каждой точке интервала I, то функция f возрастает
на I.
Достаточный признак убывания функции. Если <0 в каждой точке интервала I, то функция f убывает на I.
Необходимое и достаточное условие постоянства функции. Функция постоянна на интервале I тогда и
только тогда, когда=0 в каждой точке этого интервала.
Критические точки функции (экстремумы)
Внутренние точки области определения функции, в которых ее производная равна нулю или не
существует, называются критическими точками этой функции. Эти точки играют важную роль при
построении графика функции, поскольку только они могут быть точками экстремума функции.
Сформулируем соответствующее утверждение, его называют теоремой Ферма (в честь
французского математика Пьера Ферма).
Необходимое условие экстремума. Если точка х0 является точкой экстремума функции f и в этой точке
существует производная f′, то она равна нулю: f'(х0)= 0.
Теорема Ферма есть лишь необходимое условие экстремума: из того, что производная в точке х0
обращается в нуль, необязательно следует, что в этой точке функция имеет экстремум.
Достаточные условия существования экстремума.
Признак максимума функции. Если функция f непрерывна в точке х0, а f′ (х) > 0 на интервале (a; х0) и f′
(х0)<0 на интервале (х0; b), то точка х0 является точкой максимума функции f.
Удобно пользоваться упрощенной формулировкой этого признака:
если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума.
Признак минимума функции. Если функция f непрерывна в точке х(),
f′ (х) < 0 на интервале (а; х0) и f′ (х) > 0 на интервале (х0; b), то точка х0
является точкой минимума функции f.Удобно пользоваться упрощенной
формулировкой этого признака: если в точке х0 производная меняет знак
с минуса на плюс, то х0 есть точка минимума.

4.

Схема применения производной для нахождения
интервалов монотонности и экстремумов
1. Найти область определения функции и интервалы, на которых
функция непрерывна.
2. Найти производную f′(x).
3. Найти критические точки, т.е. точки, в которых производная
функции равна нулю или не существует.
4. В каждом из интервалов, на которые область определения
разбивается критическими точками, определить знак производной и
характер изменения функции (с помощью достаточных условий
монотонности).
5. Относительно каждой критической точки определить, является ли
она точкой максимума, минимума или не является точкой
экстремума.
6. Записать результат исследования функции: промежутки
монотонности и экстремумы.

5.

Наибольшее и наименьшее значение функции
Наибольшее и наименьшее значения непрерывной функции на отрезке.
Говорят, что функция у = f(x), определенная в промежутке X, достигает на нем
своего наибольшего (наименьшего) значения, если существует точка с,
принадлежащая этому промежутку, такая, что для всех х из X выполняется
неравенство f(x) ≤ f (с) (соответственно f(x) ≥f (с)).
Функция, непрерывная на отрезке [а, b], достигает на нем своих наибольшего и
наименьшего значений. Эти значения обозначаются так: унаиб, унаим или , .
Для функции, непрерывной на отрезке, ее наибольшее и наименьшее значения
могут достигаться как внутри отрезка, так и на его концах.
Алгоритм отыскания наибольшего и наименьшего значений непрерывной
функции
у = f(x) на отрезке [а, b].
1. Находят f'(x).
2. Находят точки, в которых f'(x) = 0 или f'(x) не существует, и отбирают из них
те, что лежат внутри отрезка [а, b].
3. Вычисляют значения функции у = f(x) в точках, полученных на предыдущем
этапе, и на концах отрезка, а затем выбирают из них наибольшее и
наименьшее; они и будут соответственно наибольшим и наименьшим
значением функции у = f(x) на отрезке [а, b].

6.

Отыскание наибольшего или наименьшего значения
функции на незамкнутом промежутке.
Задача отыскания наибольшего или наименьшего значения функции, непрерывной на интервале (а, b),
решается с помощью того же алгоритма, что и для отрезка [a, b], но на третьем этапе вместо
вычисления значений функции на концах отрезка находят пределы функции при стремлении х к
концам интервала.
Иногда для решения указанной задачи используют следующие утверждения:
1. Если функция у = f(x) имеет в промежутке X только одну точку экстремума х = с, причем это точка
максимума, то f(с) — наибольшее значение функции в промежутке X.
2. Если функция у = f(x) имеет в промежутке X только одну точку экстремума х = с, причем это точка
минимума, то f(с) — наименьшее значение функции в промежутке X.
Рассмотреть по рисунку возрастание и убывание функций.
Функция называется возрастающей на некотором промежутке
значений, если большему значению аргумента из этого интервала соответствует большее значение
функции.
Функция называется убывающей на некотором промежутке
значений, если большему значению аргумента из этого интервала соответствует меньшее значение
функции.
Возрастающие и убывающие функции называются монотонными, а промежутки, в которых функция
возрастает или убывает,- промежутками монотонности.

7.

-Дать геометрическую интерпретацию признаков возрастания и убывания функции и сформулировать признаки.
Если производная функции в данном промежутке значений положительна, то
функция возрастает в этом промежутке, а если отрицательна, то функция убывает.
Правило нахождения интервалов монотонности функции:
1. Найти производную заданной функции .
2. Приравнять производную к нулю, то есть найти критические (стационарные) точки первого рода.
3. Расположить критические точки на числовой прямой в порядке возрастания и исследовать знак производной в каждом
из полученных интервалов.
Если на каком – либо интервале у ' ( x ) 0 , на этом интервале функция у(х) возрастает,
если y ' ( x) 0, то функция у(х) убывает на этом интервале.
1 3 1 2
Пример: Найти интервалы монотонности функции y ( x) x x 12 x 5
3
2
Решение:
1. y ' ( x) 1 3x 2 1 2 x 12 x 2 x 12
3
2
x x 1
2. y' ( x) 0 x 2 x 12 0, 1 2
x1 3, x2 4
x1 x2 12
3. Разобьем числовую прямую на интервалы: ( ; 3); ( 3;4); (4; )
и определим знак производной в каждом из интервалов
х
( ; 3)
у ' ( x)
( 3;4)
0
+
у (х)
3
(4; )
4
0
-
+

8.

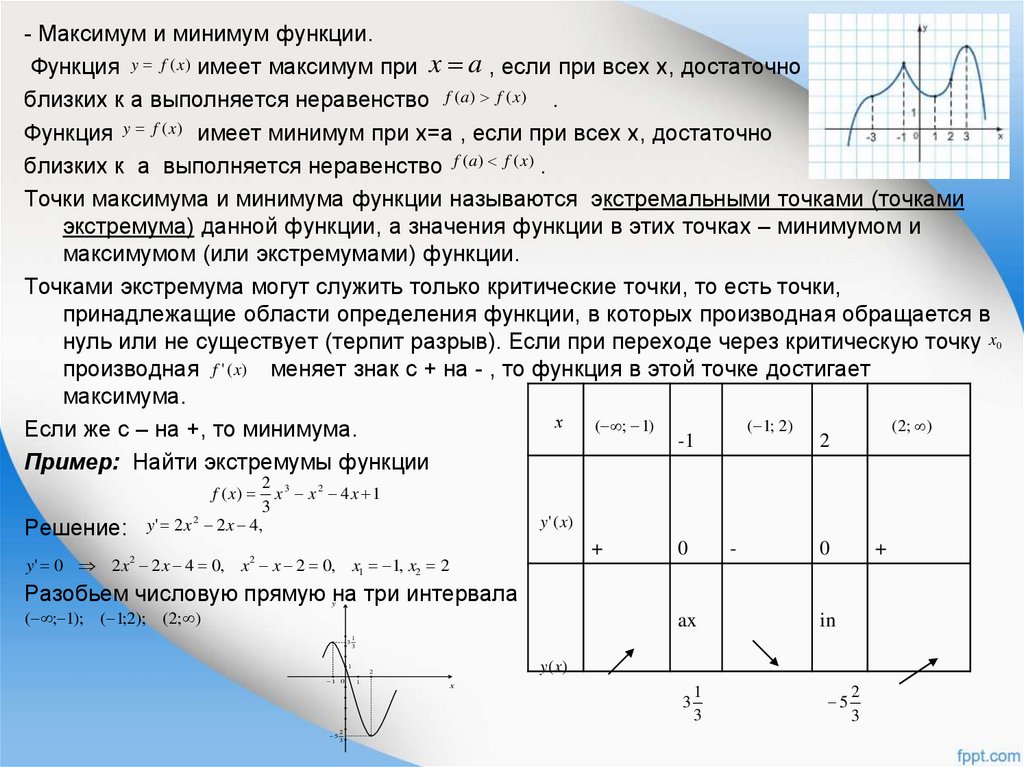
- Максимум и минимум функции.
Функция y f (x) имеет максимум при x a , если при всех х, достаточно
близких к а выполняется неравенство f (a) f ( x) .
Функция y f (x) имеет минимум при х=а , если при всех х, достаточно
близких к а выполняется неравенство f (a) f ( x) .
Точки максимума и минимума функции называются экстремальными точками (точками
экстремума) данной функции, а значения функции в этих точках – минимумом и
максимумом (или экстремумами) функции.
Точками экстремума могут служить только критические точки, то есть точки,
принадлежащие области определения функции, в которых производная обращается в
нуль или не существует (терпит разрыв). Если при переходе через критическую точку x0
производная f ' ( x) меняет знак с + на - , то функция в этой точке достигает
максимума.
х
( ; 1)
( 1; 2)
( 2; )
Если же с – на +, то минимума.
-1
2
Пример: Найти экстремумы функции
2 3
x x 2 4x 1
3
y' 2 x 2 2 x 4,
f ( x)
Решение:
y ' ( x)
+
y' 0 2 x2 2 x 4 0, x2 x 2 0, x1 1, x2 2
0
-
+
M
Разобьем числовую прямую на три интервала
( ; 1); ( 1;2); (2; )
0
M
y
ax
3
y (x)
1
2
1 0
1
x
3
5
2
3
in
1
3
1
3
5
2
3

9.

Первое правило исследования функции на экстремум.
1. Найти производную у ' ( x) заданной функции y(x) .
2. Приравнять производную к нулю, то есть найти критические (стационарные) точки
первого рода.
3. Расположить критические точки на числовой прямой в порядке возрастания и
исследовать знак производной в каждом из полученных интервалов.
Если на каком – либо интервале у ' ( x) 0 , на этом интервале функция у(х) возрастает,
если y ' ( x) 0, то функция у(х) убывает на этом интервале.
4. Если при переходе через критическую точку x0 производная f ' ( x) меняет знак с + на - , то
функция в этой точке достигает
максимума.
Если же с – на +, то минимума
y
5. Вычислить значения функции в точках экстремума.
- Пример: Исследовать на экстремум функцию y x 3 3x 2
x 0
Решение: y' 3x2 6 x, y' 0, 3x2 6 x 0, 3x( x 2) 0
x 2
x 1 ( ; 0) : y ' ( 1) 3 ( 1)( 1 2) 9 0
x 1 (0; 1) : y ' ( x) 3 1 (1 2) 0
x 3 (2; ) : y ' ( x) 3 3 (3 2) 0
1
Составим таблицу:
х
4
ymax (0) 0,
( 2; )
(0; 2)
( ; 0)
0
2
0
- 0
y ' ( x)
+
M
y (x)
0
+
M
0
2
0
ymin (2) 8 3 4 4
3
x

10.

Решить примеры:
1. Найти промежутки монотонности функции
x 1
Решение: y' 3x 2 3, 3( x 2 1) 0
x 2 ( ; 1) : y ' ( 2) 3 (2 1) 0
х 0 ( 1; 1) : у ' (0) 3 (0 1) 0
x 2 (1; ) : y ' (2) 3 (4 1) 0
y x 3 3x 1
x 1
Пример 2. Исследовать на экстремум функцию
5
Решение: y' 2 x 5, y' 0, 2 x 5 0 x
5
5
x 1 ( ; ) : y ' 2 1 5 0
2
2
5
x 3 ; : y ' (3) 2 3 5 0
2
y x 2 5x 6
2
25
5
25 50
25
49
1
5
y max
5 6
6
6
12
4
2
4
4
4
4
4
2

11.

Функция f(x)
Первая производная f'(x)
y = const
(C)'=0
y=x
y` = 1
y = xn
y' = nxn-1
y = ax
y' = axln(a)
y = ex
y' = ex
y=kx +b
y`=k
1
x
y
y
у
y = loga(x)
1
x2
1
x ln a
y = ln(x)
y' = 1/x
y = sin(x)
y' = cos(x)
y = cos(x)
y' = -sin(x)
y = tg(x)
y' = 1/cos2(x)
y = ctg(x)
y
y = arcsin(x)
y = arccos(x)
y = arctg(x)
y' = -1/sin
1 2(x)
y
1 x2
1
1 x2
y' = 1/(1+x2)
2