Решение задач. Подобные треугольники. Определение. Подобные фигуры

1.

2.

Определение. Подобные фигуры –это геометрические
фигуры, которые имеют одинаковую форму.

3.

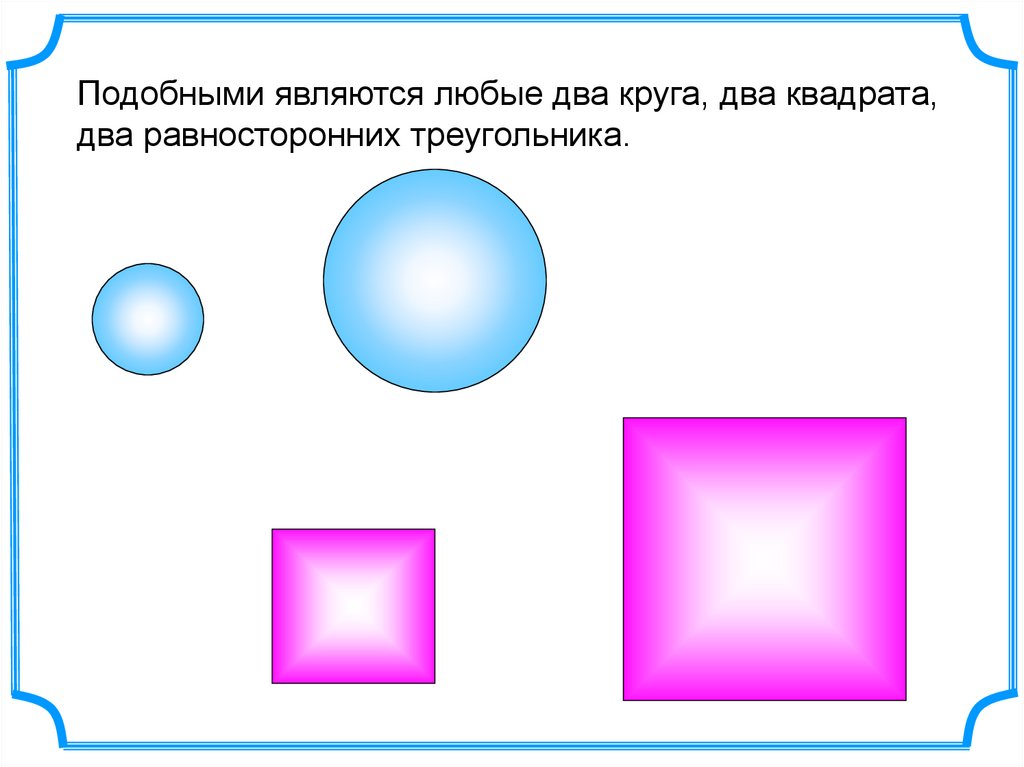
Подобными являются любые два круга, два квадрата,
два равносторонних треугольника.

4.

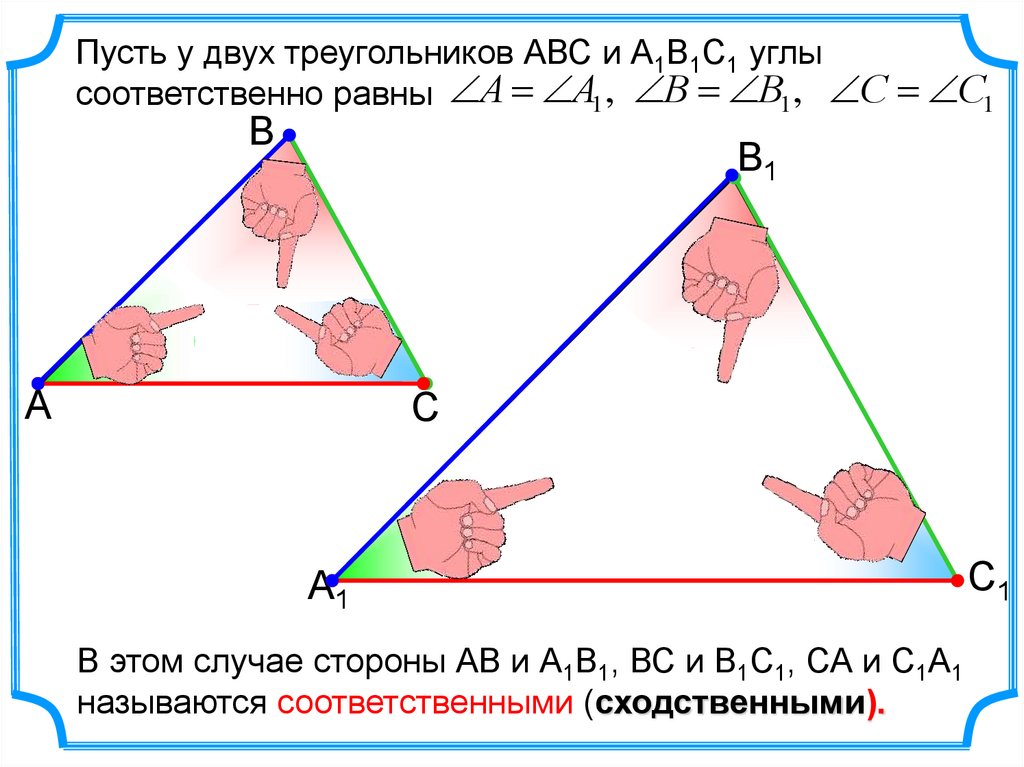
Пусть у двух треугольников АВС и А1В1С1 углы
соответственно равны А А1 , В В1 , С С1
В
В1
А
С
А1
В этом случае стороны АВ и А1В1, ВС и В1С1, СА и С1А1
называются соответственными (сходственными).
С1

5.

Два треугольника называются подобными, если их углы
соответственно равны и стороны одного треугольника
пропорциональны соответственным сторонам другого
треугольника.
А А1 , В В1 , С С1
В
АВ
ВС
АС
А1 В1 В1С1 А1С1
В1
А
С
А1
С1

6.

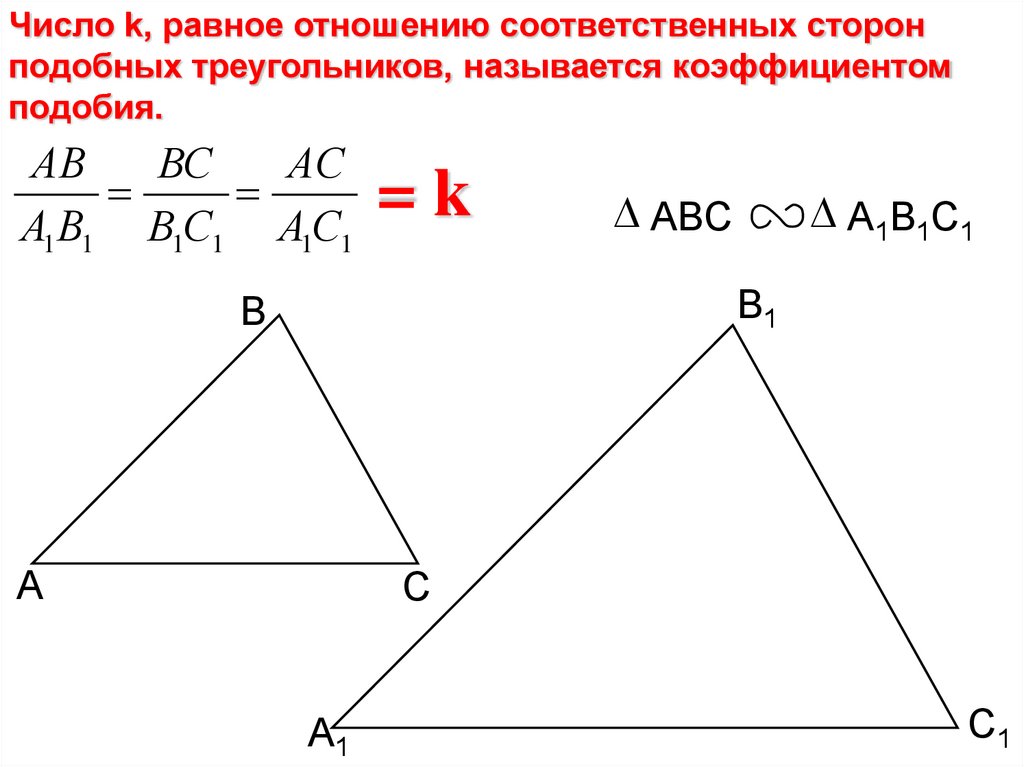
Число k, равное отношению соответственных сторон
подобных треугольников, называется коэффициентом
подобия.
АВ
ВС
АС
=
k
А1 В1 В1С1 А1С1
ABC
A1B1C1
В1
В
А
С
А1
С1

7.

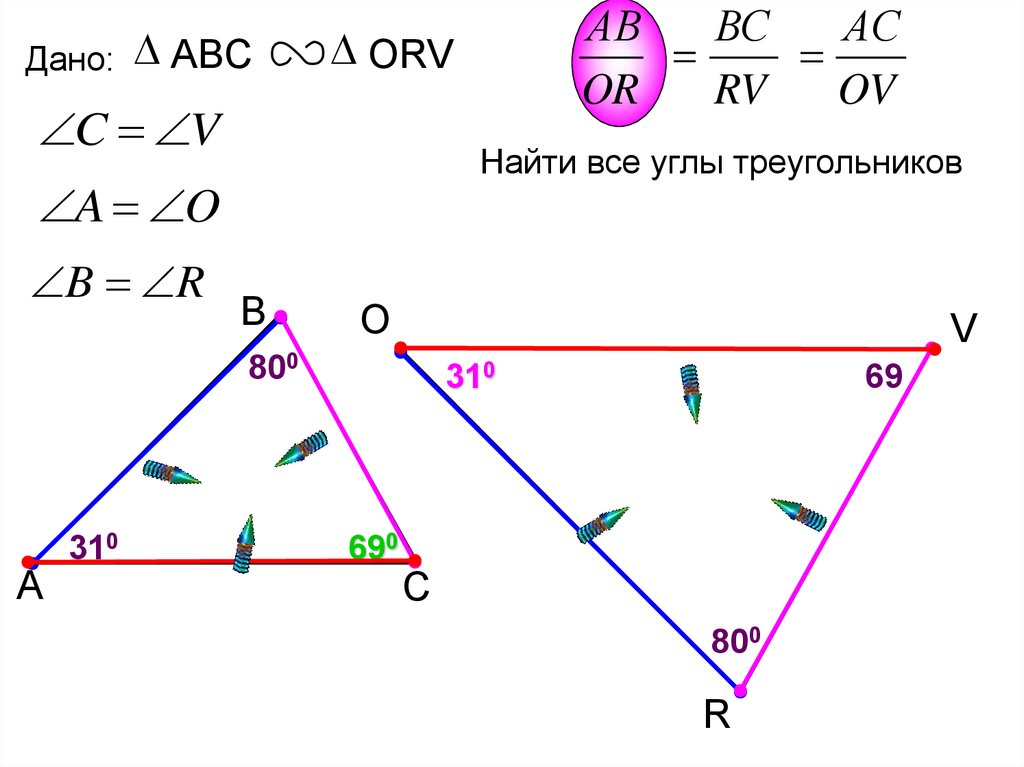
Дано: ABC
ORV
C V
Найти все углы треугольников
A O
B R
В
O
V
800
А
310
АВ
ВС
АС
OR
OV
RV
310
690
69
С
800
R

8.

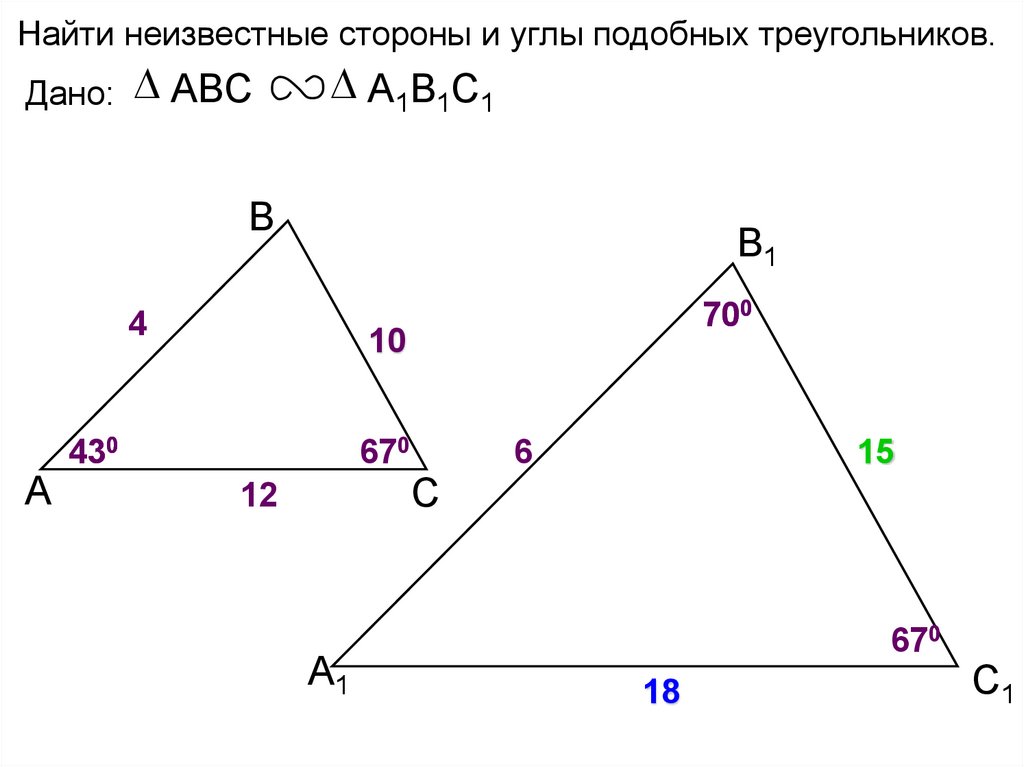
Найти неизвестные стороны и углы подобных треугольников.
Дано: ABC
А1В1С1
В
В1
4
А
700
10
430
670
12
А1
С
6
15
670
18
С1

9.

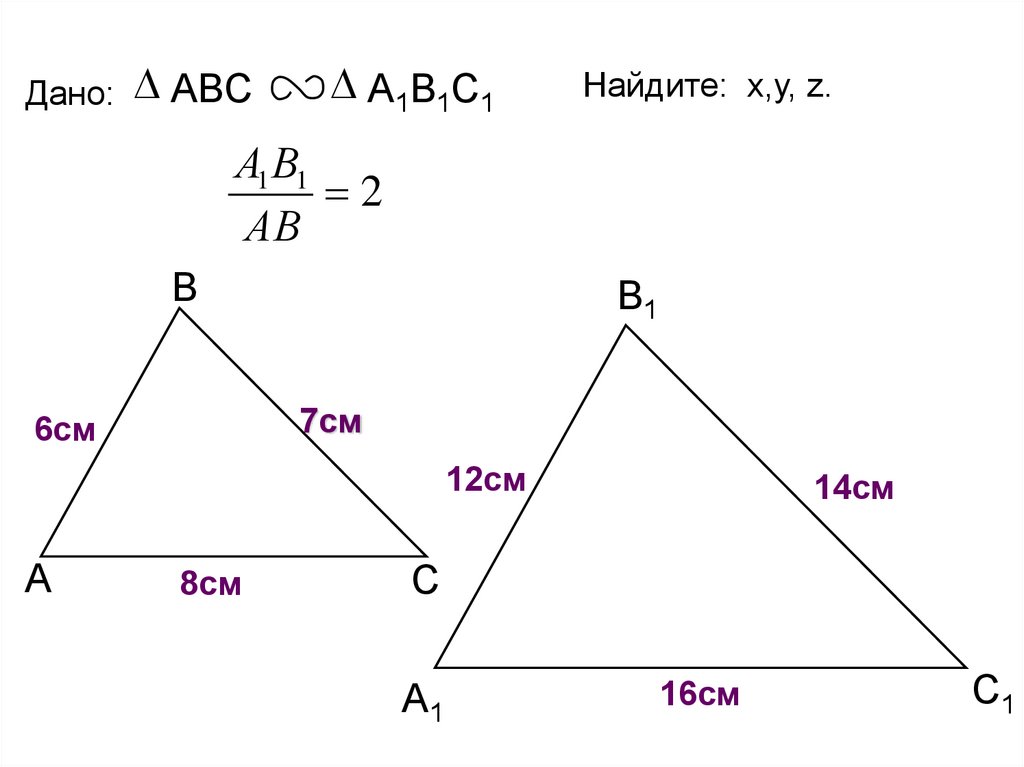
Дано: ABC
А1В1С1
Найдите: x,у, z.
А1 В1
2
АВ
В
В1
7см
6см
12см
х
А
8см
14см
у
С
А1
16см
z
С1

10.

Дано: ABC
А1В1С1
Найдите: х, у, z.
А1 В1
2
АВ
В
В1
10,5см
у
9смх
18см
А
12см
z
21см
С
А1
24см
С1

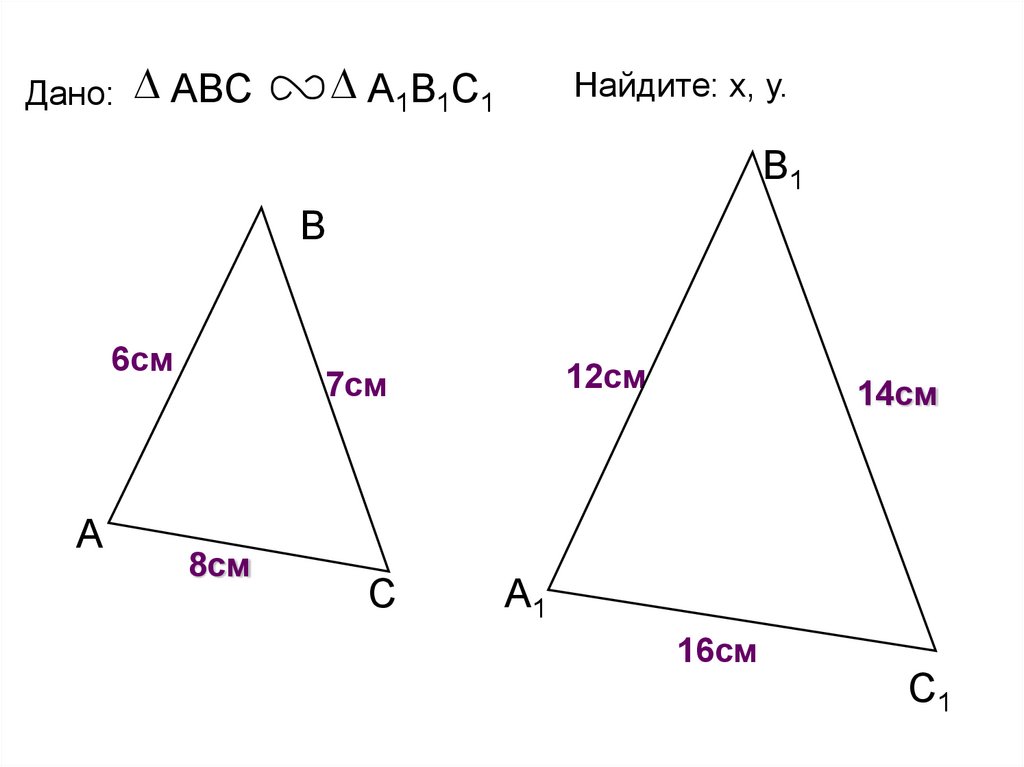
11.

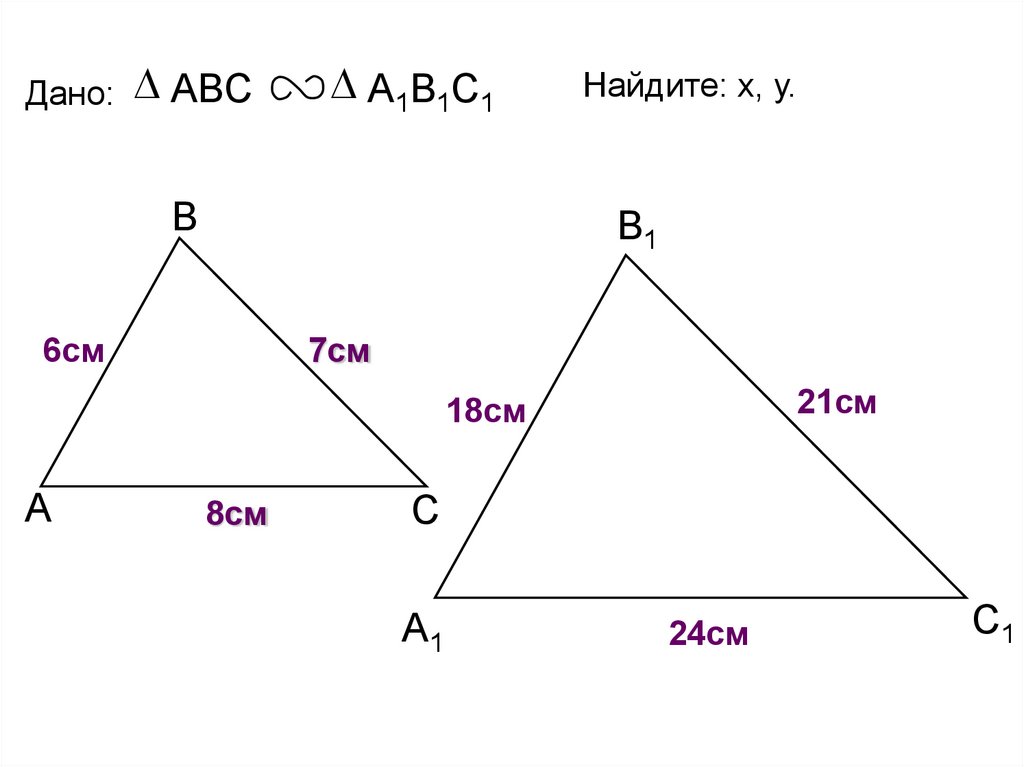
Дано: ABC
А1В1С1
В
Найдите: х, у.
В1
6см
7см
21см
х
18см
А
8см
С
А1
у
24см
С1

12.

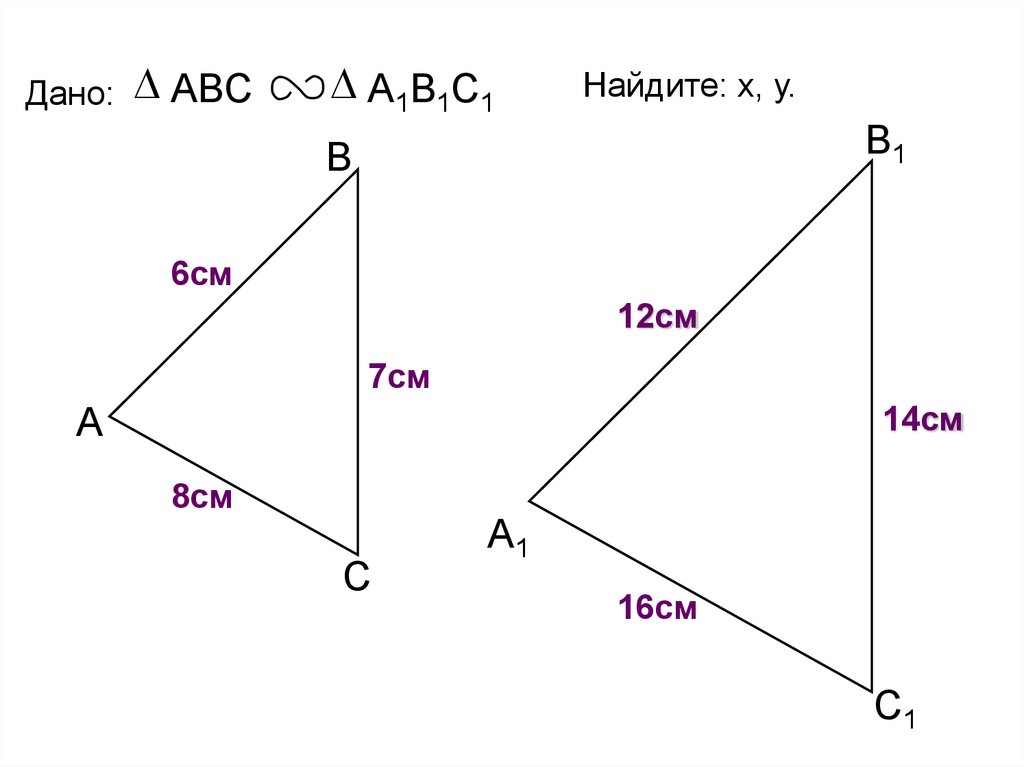
Дано: ABC
А1В1С1
Найдите: х, у.
В1
В
6см
х
12см
7см
у
А
14см
8см
С
А1
16см
С1

13.

Дано: ABC
А1В1С1
Найдите: х, у.
В1
В
6см
А
х
7см
8см
С
12см
А1
14см
у
16см
С1

14.

Дано: ABC
A1B1C1
k – коэффициент подобия
Отношение периметров двух
подобных треугольников
равно коэффициенту подобия.
РABC
k
РA1B1C1

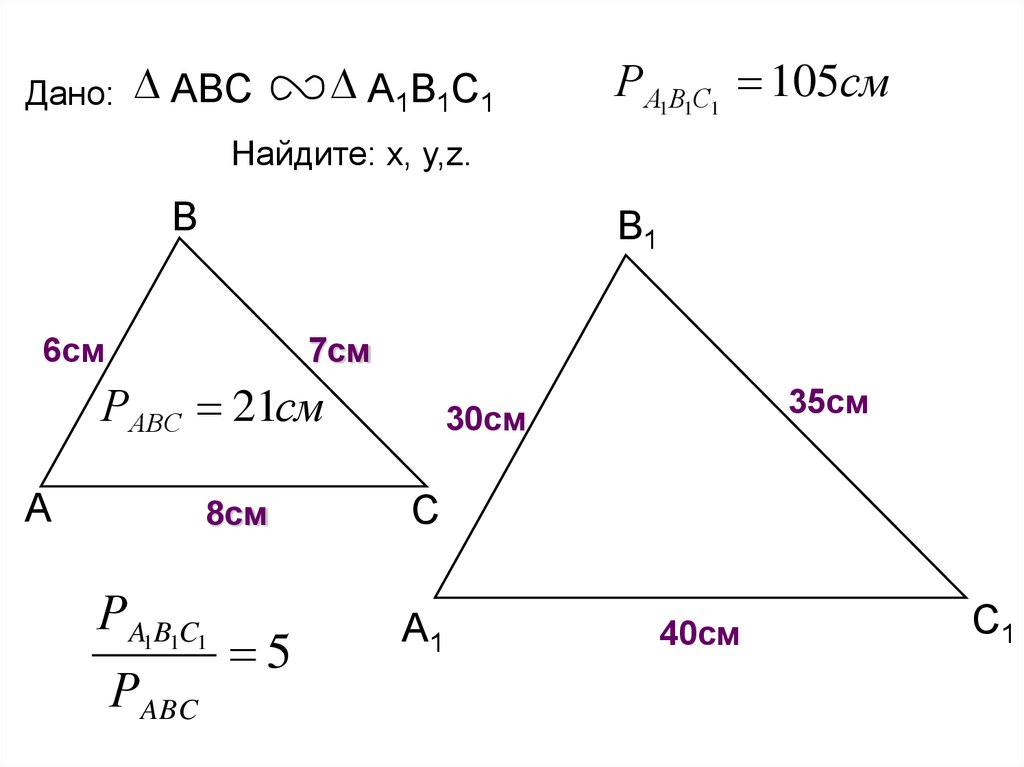
15.

Дано: ABC
А1В1С1
Р А1В1С1 105см
Найдите: х, у,z.
В
В1
6см
7см
РАВС 21см
А
8см
РA1B1C1
РABC
5
35см
y
х
30см
С
А1
z
40см
С1

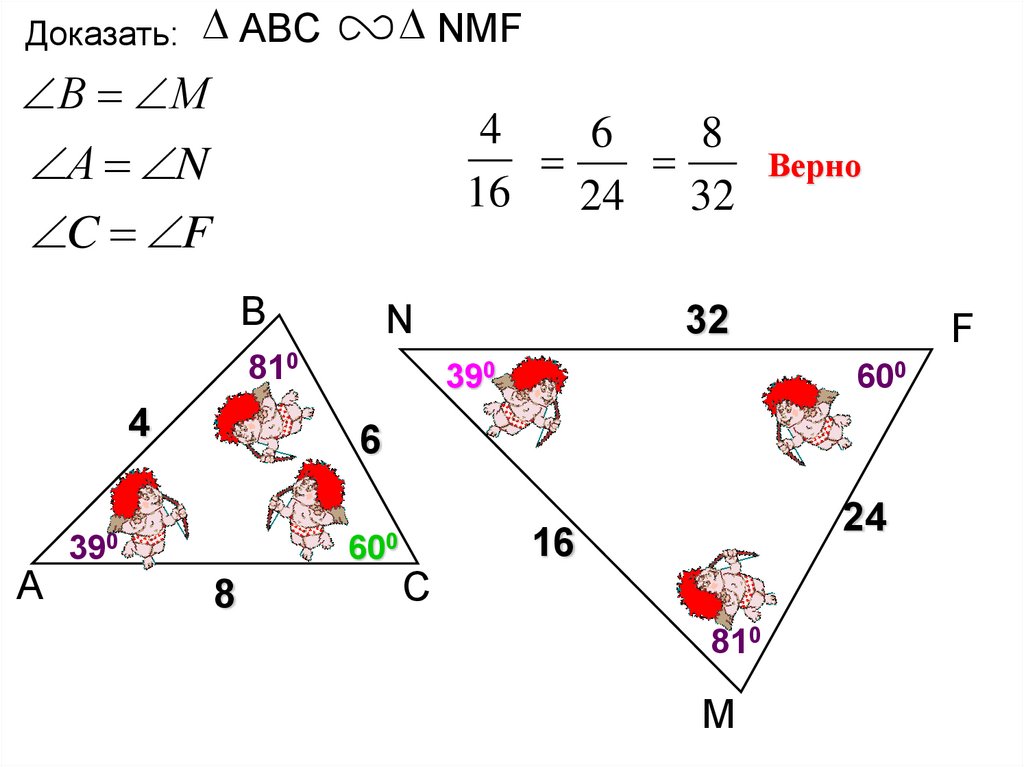
16.

Доказать: ABC
NMF
В М
4
6
8
16
24 32
А N
C F
В
N
810
4
А
Верно
32
390
F
600
6
390
600
8
24
16
С
810
М