Similar presentations:
Расстояние от точки до прямой
1.
Данная презентация используется на факультативных и элективныхзанятиях при подготовке выпускников к сдаче ЕГЭ
Цель: Повторить и обобщить материал по теме «Решение
стереометрических задач при подготовке к ЕГЭ» и применить
полученные знания в практической деятельности при решении задач.
Задачи:
Учебная: Закрепить знания и умение решать стереометрические задачи;
применять ранее приобретенные знания к решению геометрических
задач.
Развивающая: Развивать математическую логику, креативное
мышление, пространственное воображение, навыки самостоятельной
и творческой деятельности.
Воспитательная: Воспитывать интерес к предмету, точность и
аккуратность в построении чертежа к геометрической задаче.
Презентация отражает следующие вопросы геометрии:
• Расстояние от точки до прямой;
• Расстояние от точки до плоскости;
• Расстояние между двумя прямыми.
2.
3.
Расстояние от точки до прямой – этодлина перпендикуляра, проведённого из
данной точки к данной прямой.
4. Дано: АВСДА1В1С1Д1 – куб. АВ = 1. Найти: Расстояние от точки С до прямой ВД1.
Решение:1. ∆ВСД1– прямоугольный ( по теореме о трёх
перпендикулярах), ∠Д1СВ – прямой.
2. СН – высота ∆ВСД1, значит СВ – среднее
пропорциональное между ВН и ВД1, тогда
ВН
СВ
;
СВ ВД 1
ВН
1
;
1
3
СНВ
получаем
Из
ВН
3
3
2
3
1
2
1
СН 1
3
3
2
6
3
3
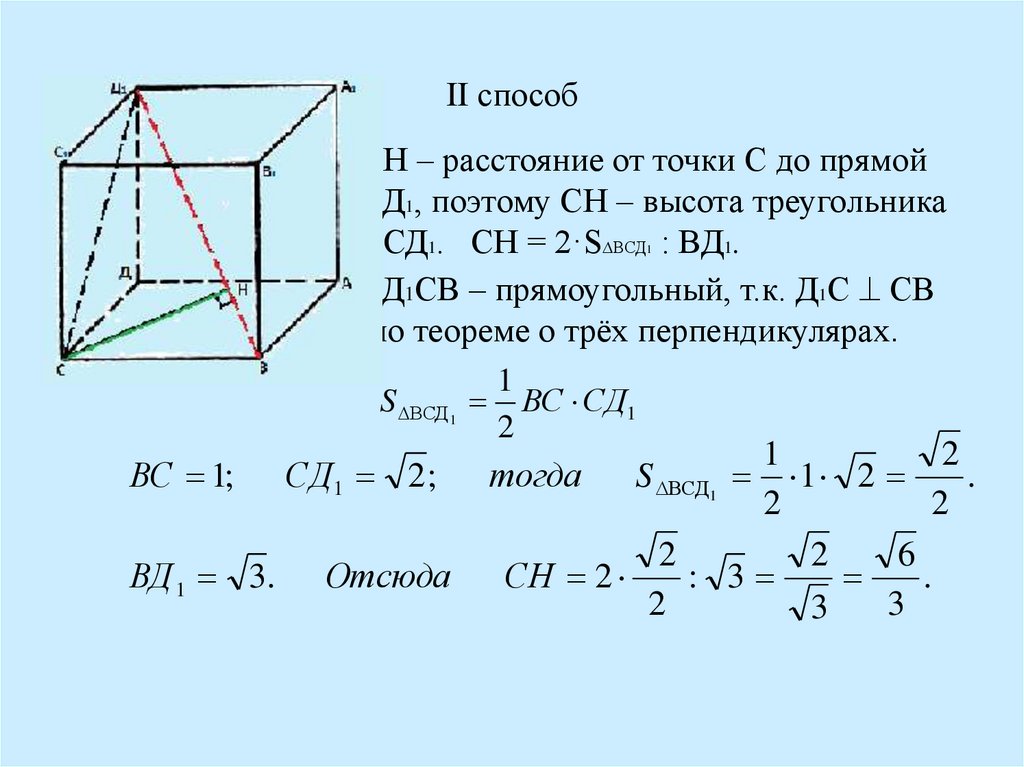
5. II способ
СН – расстояние от точки С до прямойВД1, поэтому СН – высота треугольника
ВСД1. СН = 2·S∆ВСД : ВД1.
∆Д1СВ – прямоугольный, т.к. Д1С СВ
по теореме о трёх перпендикулярах.
1
S ВСД1 ВС СД1
2
1
2
СД 1 2 ; тогда
S ВСД1 1 2
.
2
2
1
ВС 1;
ВД 1 3.
Отсюда
2
СН 2
: 3
2
2
6
.
3
3
6.
7. Расстояние от точки до плоскости – это длина перпендикуляра, проведённого из точки А к плоскости.
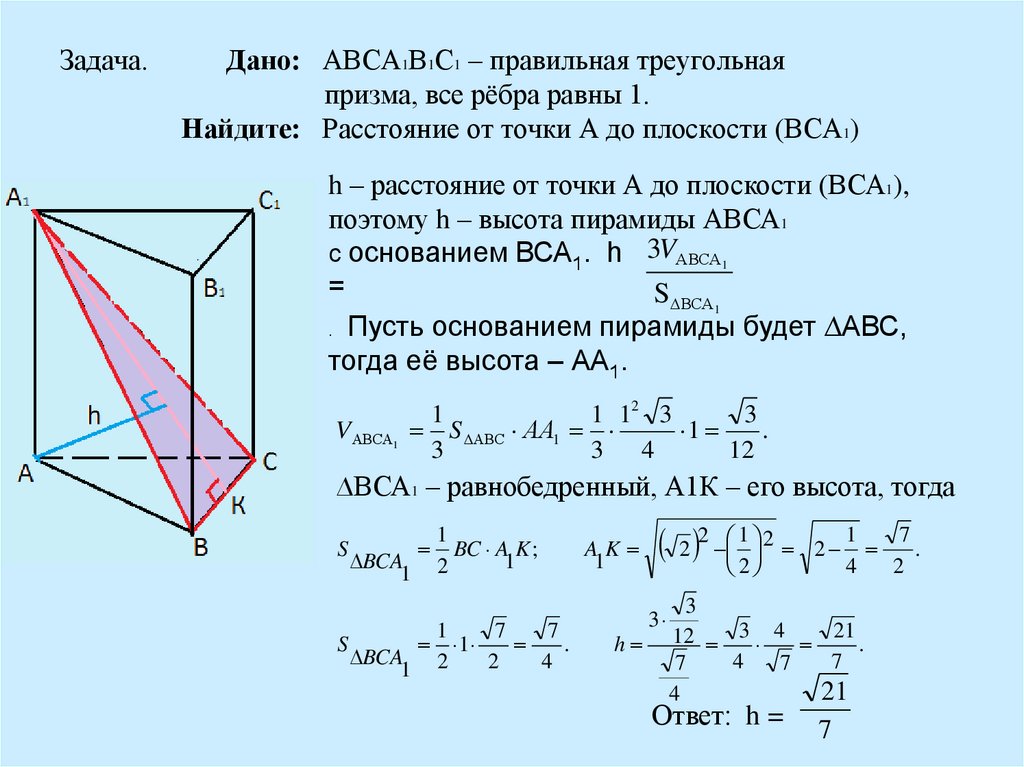
8. Задача. Дано: АВСА1В1С1 – правильная треугольная призма, все рёбра равны 1. Найдите: Расстояние от точки А до плоскости (ВСА1)
h – расстояние от точки А до плоскости (ВСА1),поэтому h – высота пирамиды АВСА1
с основанием ВСА1. h 3VАВСА1
=
S ВСА1
. Пусть основанием пирамиды будет ∆АВС,
тогда её высота – АА1.
1
1 12 3
3
VАВСА1 S АВС АА1
1
.
3
3 4
12
∆ВСА1 – равнобедренный, А1К – его высота, тогда
S
S
BCA
1
BCA
1
1
BC A K ;
1
2
1
7
7
1
.
2
2
4
AK
1
h
2 2 12 2 2 14 27 .
3
3
12 3 4 21 .
4
7
7
7
21
4
Ответ: h =
7
9. За страницами учебника Расстояние от точки А до плоскости можно вычислить по формуле:
hax0 by0 cz0 d
a2 b2 c2
, где ax by cz d 0
уравнение плоскости, А( x0 ; y0 ; z0 ).
10.
31
1
В
; 0; 0 , С 0; ; 0 , А1 0; ; 1 ,
2
2
2
тогда
3 1
3
1
ВС
; ; 0 ; ВА1
; ; 1
2
2
2
2
n a; b; c (ВСА1 )
они лежат в плоскости (ВСА1).Рассмотрим
и найдём его координаты.
n ВС, n ВА1 , тогда получаем систему уравнений:
3
1
a b 0c 0
2
2
3 a 1 b 1c 0
2
2
3a 3a 2c 0,
b 3
3
c c,
3
3a b 0
3a b 2c 0
2 3a 2c 0,
2 3 a 2c,
3
1
x y z 0 6
2
2
2 3 6 y 6 z 3 0 уравнение плоскости ВСА 1 ,
h
b 6,
3 3
12 36 36
6
84
,
d 3 тогда
c 6,
a
3
n ; 1; 1
3
тогда
3
3
х
1 у 0 1 z 0 0,
3
2
а 2 3,
отсюда b 3a,
6
2 21
3 21
21
21
7
где
2c
2 3
3
c
3
11.
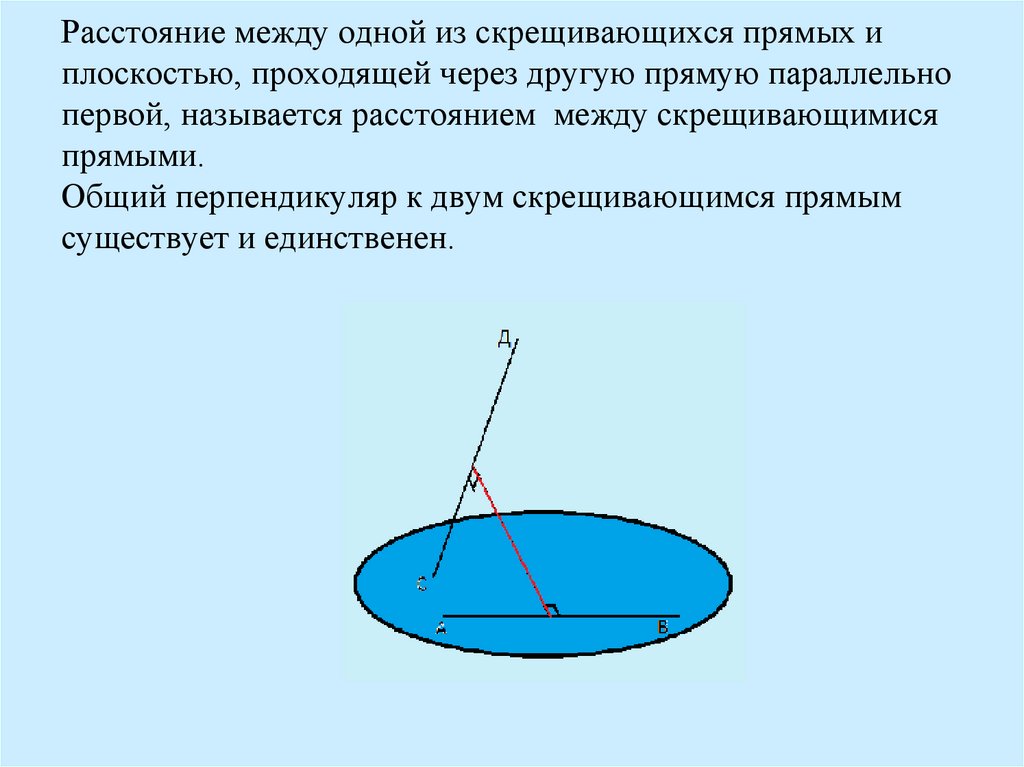
12. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется
расстоянием между скрещивающимисяпрямыми.
Общий перпендикуляр к двум скрещивающимся прямым
существует и единственен.
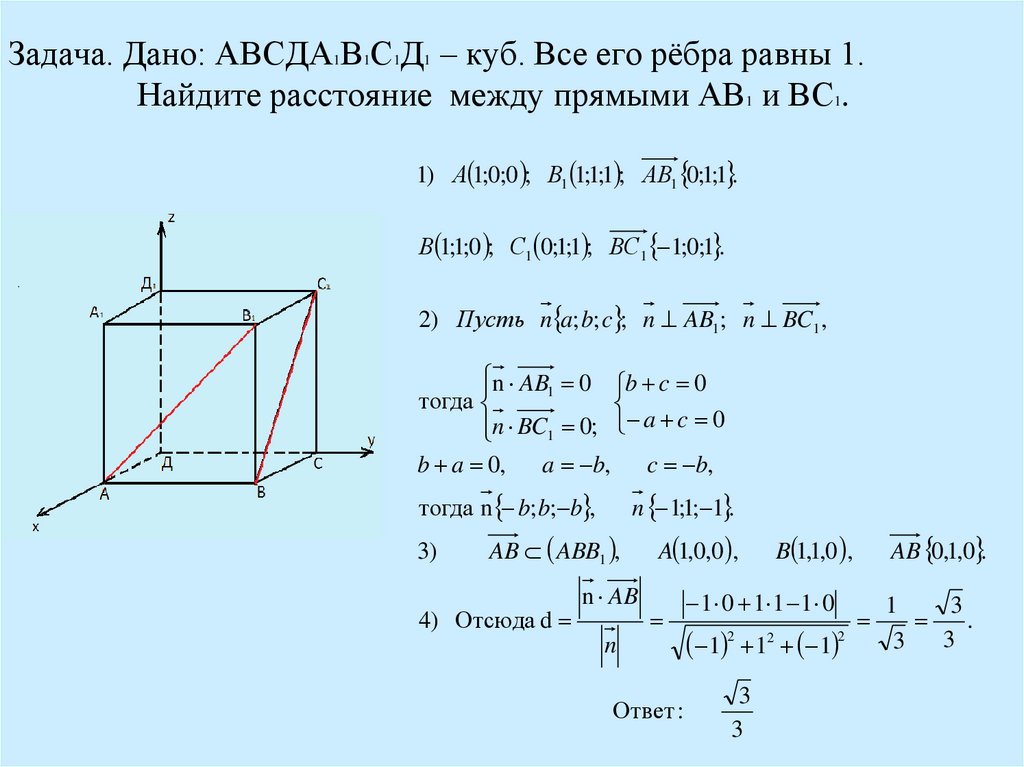
13. Задача. Дано: АВСДА1В1С1Д1 – куб. Все его рёбра равны 1. Найдите расстояние между прямыми АВ1 и ВС1.
ВС1 ВДС1 ;АВ1 АВ1 Д1 ;
ВДС1 АВ1 Д1
следовательно расстояние между скрещивающимися
прямыми ВС1 и АВ1 равно расстоянию между
соответствующими плоскостями. Диагональ СА1
перпендикулярна этим плоскостям.
СА1 ∩ (ВДС1) = F;
CА1 ∩ (АД1В1) = Е.
EF – расстояние между ВС1 и АВ1.
В ∆ АСЕ отрезок ОF ║ АЕ и проходит через середину
отрезка АС, следовательно ОF – средняя линия
треугольника АСЕ и, значит, ЕF = FC. Аналогично,
О1Е – средняя линия треугольника А1С1F
1
3
А1 Е ЕF . Отсюда ЕF СА1
.
3
3
3
Ответ :
3
14. За страницами учебника
Расстояние между скрещивающимисяпрямыми можно найти по формуле:
n m
d
n
15.
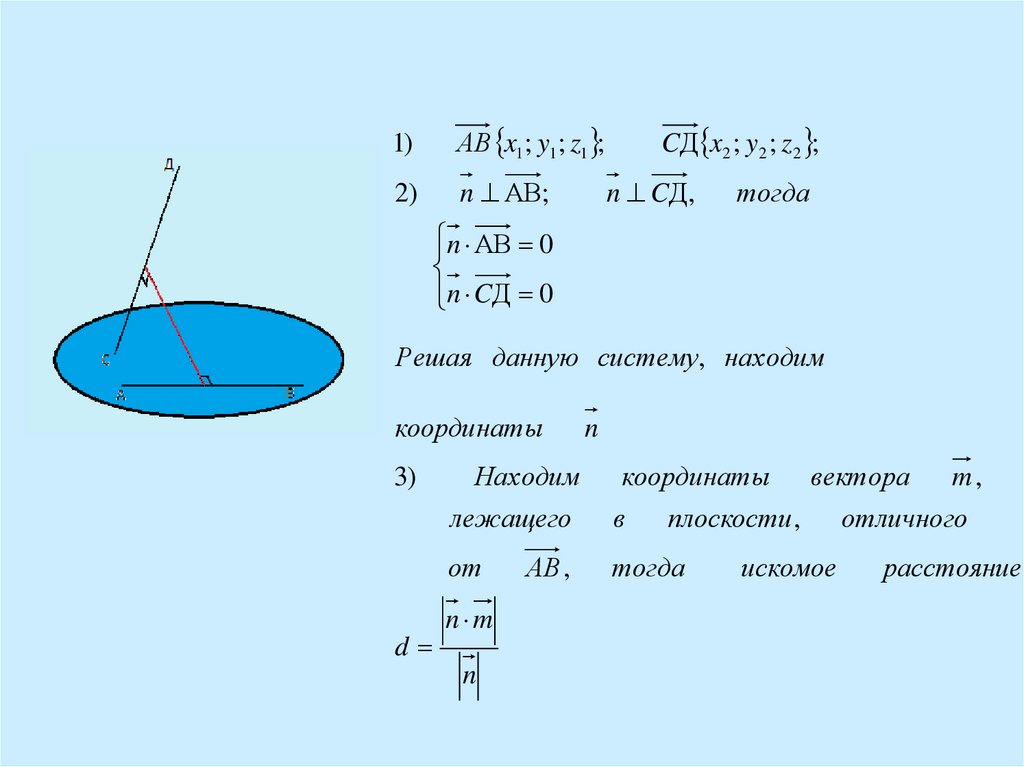
1)АВ x1 ; y1 ; z1 ;
2)
n АВ;
CД x2 ; y2 ; z 2 ;
n CД ,
тогда
n АВ 0
n CД 0
Решая данную систему, находим
координаты
3)
d
n
Находим
лежащего
координаты вектора
m,
в
плоскости, отличного
от
тогда
n m
n
АВ ,
искомое
расстояние
16. Задача. Дано: АВСДА1В1С1Д1 – куб. Все его рёбра равны 1. Найдите расстояние между прямыми АВ1 и ВС1.
1) А 1;0;0 ; В1 1;1;1 ; АВ1 0;1;1 .В 1;1;0 ; С1 0;1;1 ; ВС1 1;0;1 .
2) Пусть n a; b; c ; n AB1 ; n BC1 ,
n AB1 0 b c 0
тогда
n BC1 0; a c 0
b a 0,
a b, c b,
тогда n b; b; b ,
3)
n 1;1; 1 .
AB ABB1 ,
4) Отсюда d
n AB
A 1,0,0 ,
n
Ответ :
B 1,1,0 ,
1 0 1 1 1 0
1 2 12 1 2
3
3
AB 0,1,0 .
1
3
.
3
3
17. Задача 2. Дано: SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1. Найдите: Расстояние между прямыми АS и
ВС.2
2
2
2
; AS
1) А
;0;0 ; S 0;0;
;
0
;
2
2
2
2
2
2
2
2
B 0;
;0 ; C
;0;0 ; CB
;
;0
2
2
2
2
2) n a; b; c , n AS ; n CB,
2
2
а
с 0
2
2
2 а 2b 0
2
2
b c 0,
b c,
тогда
a c 0
a b 0
a c,
n 1; 1;1
2
2
3) SB SBC ; SB 0;
;
2
2
0 1
4) d
2
2
1
1
2
2
12 1 12
2
Ответ :
6
3
2
3
2
3
6
.
3
18. Литература:
• Геометрия 10 – 11 классы. Учебник дляобщеобразовательных учреждений. Базовый и
профильный уровни. Авторы: Л.С. Атанасян,
В.Ф.Бутузов, С.Б.Кадомцев, Л.С.Киселева,
Э.Г.Позняк Москва «Просвещение» 2013 год
• Избранные вопросы профильного и
предпрофильного курса математики. Авторы:
И.Г.Малышев, М.А. Минчасова, Б.Н.Иванов. Нижний
Новгород Нижегородский гуманитарный центр, 2007
год
• ЕГЭ 2011 Математика Задача С2 Геометрия
Стереометрия Под редакцией А.Л.Семенова и
И.В.Ященко Москва Издательство МЦНМО 2011













 mathematics
mathematics








