Similar presentations:
Моделирование. Этапы моделирования
1. Моделирование
1Моделирование
Этапы моделирования
2. I. Постановка задачи
2I. Постановка задачи
• исследование оригинала
изучение сущности объекта или явления
• анализ («что будет, если …»)
научиться прогнозировать последствий при различных
воздействиях на оригинал
• синтез («как сделать, чтобы …»)
научиться управлять оригиналом, оказывая на него
воздействия
• оптимизация («как сделать лучше»)
выбор наилучшего решения в заданных условиях
3. I. Постановка задачи
3I. Постановка задачи
Хорошо поставленная задача:
• описаны все связи между исходными данными и
результатом
• известны все исходные данные
• решение существует
• задача имеет единственное решение
Примеры плохо поставленных задач:
• Уроки в школе начинаются в 830. В 1000 к школе подъехал
красный автомобиль. Определите, когда Вася выйдет
играть в футбол?
• Вася бросает мяч со скоростью 12 м/с. Где мяч впервые
ударится о землю?
• Решить уравнение sin x = 4 (нет решений).
• Найти функцию, которая проходит через точки (0,1) и (1,0)
(бесконечно много решений).
4. I. Постановка задачи (пример)
4I. Постановка задачи (пример)
Спортсмен Вася в синей кепке бросает белый мяч со
скоростью 12 м/с. Под каким углом к горизонту ему нужно
бросить мяч, чтобы попасть в желтую мишень?
Допущения:
Мишень расположена на высоте 4 м на расстоянии 10
м от Васи. В момент броска мяч находится на высоте
2 м от земли.
5. II. Разработка модели
5II. Разработка модели
Спортсмен Вася в синей кепке бросает белый мяч со
скоростью 12 м/с. Под каким углом к горизонту ему нужно
бросить мяч, чтобы попасть в желтую мишень? Мишень
расположена на высоте 4 м на расстоянии 10 м от Васи.
В момент броска мяч находится на высоте 2 м от земли.
1) Определить существенные исходные данные.
• мяч и мишень — материальные точки
• мишень неподвижна
• сопротивление воздуха не учитывается.
2) Выбор типа модели.
6. II. Разработка модели
6,
II. Разработка модели
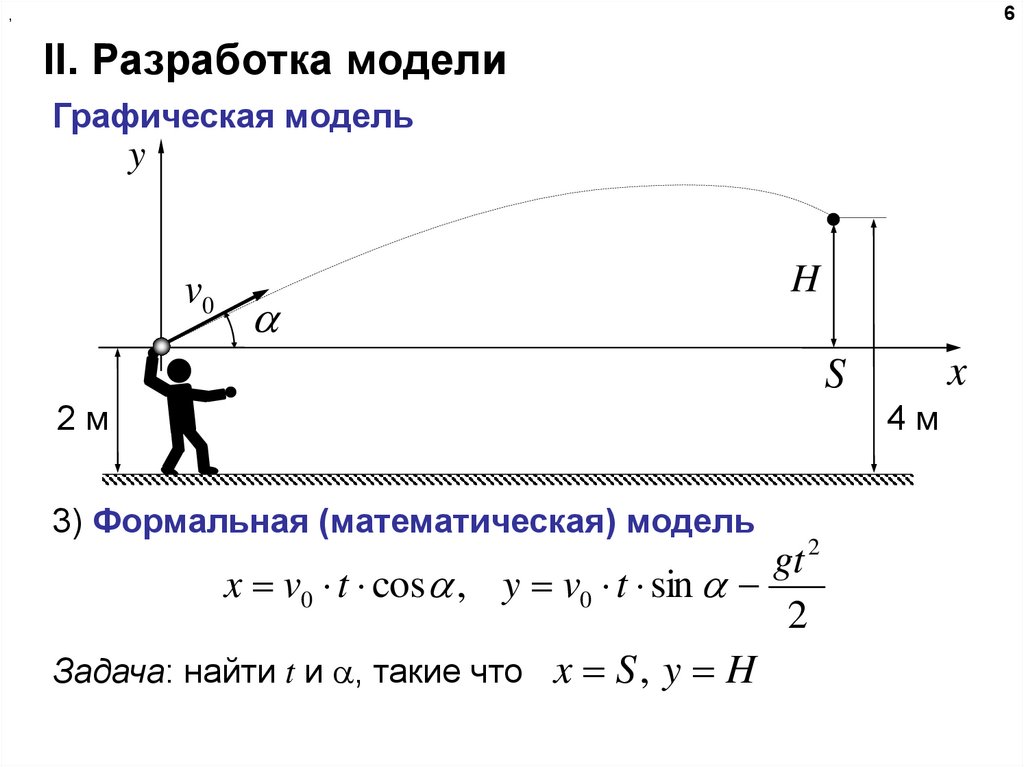
Графическая модель
y
v0
H
x
S
2м
3) Формальная (математическая) модель
gt 2
x v0 t cos , y v0 t sin
2
Задача: найти t и , такие что x S , y H
4м
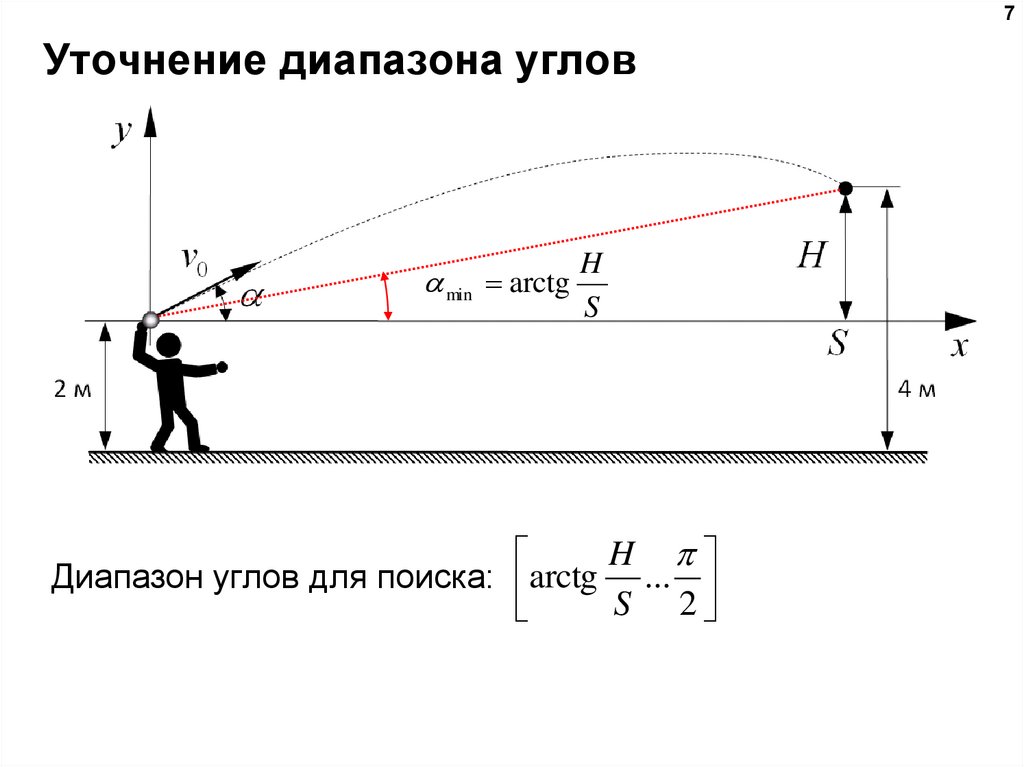
7. Уточнение диапазона углов
7Уточнение диапазона углов
min arctg
H
S
H
Диапазон углов для поиска: arctg ...
S 2
8. II. Разработка модели
8II. Разработка модели
4) Алгоритм моделирования
Метод I.
Меняем угол . Для выбранного угла строим
траекторию полета мяча. Если она проходит выше
мишени, уменьшаем угол, если ниже – увеличиваем.
Метод II.
Из первого равенства выражаем время полета:
v0 cos t S
S
t
v0 cos
Меняем угол . Для выбранного угла считаем t, а
затем – значение y при этом t. Если оно больше H,
уменьшаем угол, если меньше – увеличиваем.
не надо строить всю траекторию для каждого
9. II. Разработка модели
9II. Разработка модели
5) Компьютерная модель
• программа (Паскаль, Си, …)
• электронные таблицы (Excel, OpenOffice.org Calc)
• среды моделирования (Simulink, VisSim)
10. III. Тестирование модели
10III. Тестирование модели
Тестирование – это проверка модели на простых
исходных данных с известным результатом.
а) тестирование математической модели:
gt
x v0 t cos , y v0 t sin
2
2
• при t = 0 x = 0, y = 0 (в начале координат)
gt 2
• при v0 = 0 x = 0, y
(падение вниз)
2
• при = 90 x = 0
• при увеличении t парабола «загибается» вниз
б) тестирование компьютерной модели:
(пробные расчёты в рассмотренных условиях)
11. IV. Эксперимент с моделью
11IV. Эксперимент с моделью
Эксперимент – это исследование модели при тех
исходных данных, которые нас интересуют (результат
заранее неизвестен).
1) задаём угол
S
2) находим время t
v0 cos
3) находим высоту
gt 2
t cos , y v0 t sin
2
Может быть два
решения!
y<H
H
Диапазон углов для поиска: arctg ...
S 2
? Как отделить два решения?
построить график y( )
12. V. Анализ результатов эксперимента
12V. Анализ результатов эксперимента
! Необходима проверка на оригинале!
Возможные выводы:
• задача решена, модель адекватна
• необходимо изменить алгоритм или условия
моделирования
• необходимо изменить модель (учесть
дополнительные свойства)
• необходимо изменить постановку задачи
13. V. Анализ результатов
13V. Анализ результатов
• всегда ли Вася сможет попасть в мишень?
• если начальная скорость отличается от заданной?
• если мяч и мишень не считать материальными
точками?
• как сильно влияет сопротивление воздуха?
• если мишень качается?
• и т.д….
14.
14Задача: Составить алгоритм определения высоты снаряда над землей на расстоянии L от пушки, снаряд вылетел под углом а, а со скоростью V.
1) Постановка задачи:
Дано.
L,a,v - вещественные переменные.
Надо.
Высота снаряда над землей - Н - вещественная переменная.
Форма представления модели: Математическая.
Переведем угол полета снаряда в радианы: d = а*3.1415/180.
Вычислим время полета: t = L / (cos(d)*v).
Высота, снаряда над землей на расстоянии L от пушки:
H=L*tg(d) - 9.8*t*t/2.
15.
Задача: Составить алгоритм определения высоты снаряда над зем-15лей на расстоянии L от пушки, снаряд вылетел под углом а, а со скоростью V.
2) Разработка модели: Построим компьютерную модель (программу,
реализующую данные вычисления на школьном алгоритмическом
языке).
Выбранные переменные d. t - промежуточные переменные
вещественного типа. Они описыются после служебного слова нач .
Переменные L,a,v в данном алгоритме являются аргументами.
Переменная H является результатом. Аргумент и результат
описываются в заголовке алгоритма, после указания его имени.
алг Высота (арг вещ L,a,.v, рез вещ H)
нач вещ d,t
d:=a*3.1415/180
t:=L/(cos(d)*v)
H:=L*sin(d)/cos(d)-9.8*t*t/2
кон
16.
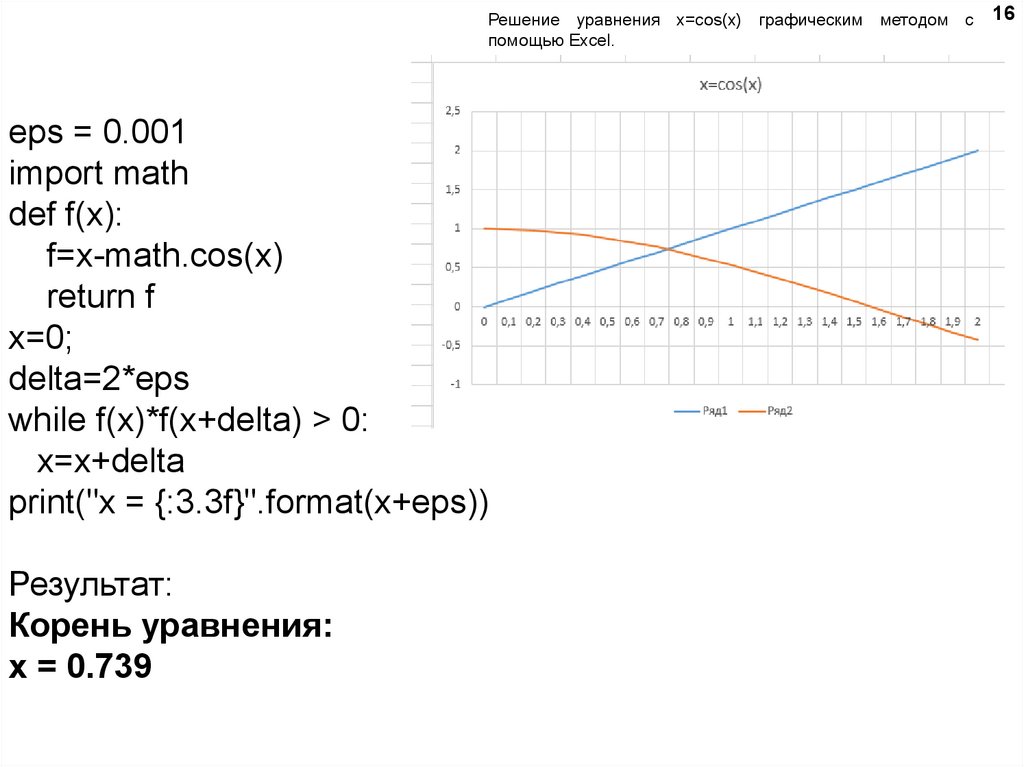
Решение уравнения x=cos(x) графическим методом спомощью Excel.
eps = 0.001
import math
def f(x):
f=x-math.cos(x)
return f
x=0;
delta=2*eps
while f(x)*f(x+delta) > 0:
x=x+delta
print("x = {:3.3f}".format(x+eps))
Результат:
Корень уравнения:
x = 0.739
16
17.
17Уравнение траектории:
Пример программы, моделирующей поиск угла для попадания мяча
в мишень.
def f(x):
f=hh-h-s*math.tan(x) + (g*s*s)/(2*v0*v0*math.cos(x)*math.cos(x))
return f
while a1 < 90:
x= 2*pi*a1/(360)
delta1= 2*pi*delta/(360)
if f(x)*f(x+delta1) < 0:
print("a1={:6.1f} ".format(a1))
a1=a1+delta














 informatics
informatics








