Системы счисления

1. Системы счисления

2.

В существующих ЭВМ:
Старший разряд
№7
№6 №5
№4
№3
Младший разряд
№2 №1 №0
1
1
1
0
0
0
1
0
Машинное слово
Разряд, иначе - бит, bit = binary digit
= двоичная цифра
Цели занятия:
1. Разобраться, почему для хранения информации в компьютерах применяются
устройства, кодирующие любую информацию в форме 1 или 0;
2. Почему информация в компьютере представляется именно в двоичной системе
счисления?
3. Как переводить число из одной любой системы счисления в любую другую?
(главный вопрос – зачем это изучать? – для того, чтобы понять
принципы вычислений, реализованные в современных ЭВМ, и
оценить, насколько они эффективны (может быть, их нужно
пересмотреть?)

3.

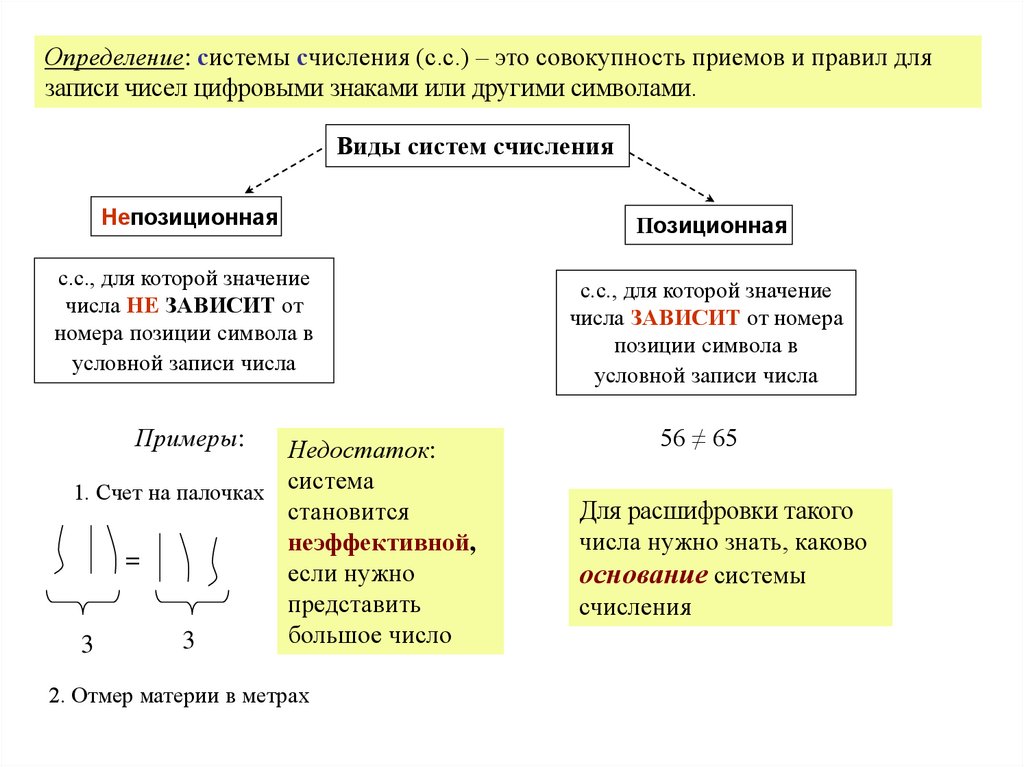
Определение: системы счисления (с.с.) – это совокупность приемов и правил для
записи чисел цифровыми знаками или другими символами.
Виды систем счисления
Непозиционная
с.с., для которой значение
числа НЕ ЗАВИСИТ от
номера позиции символа в
условной записи числа
Примеры:
Недостаток:
1. Счет на палочках система
становится
неэффективной,
=
если нужно
представить
большое число
3
3
2. Отмер материи в метрах
Позиционная
с.с., для которой значение
числа ЗАВИСИТ от номера
позиции символа в
условной записи числа
56 ≠ 65
Для расшифровки такого
числа нужно знать, каково
основание системы
счисления

4.

Требования к системам счисления
1. Должен быть задан алфавит (набор символов) для записи любых чисел
Примеры:
В десятичной с.с. используется алфавит {0, 1, …, 9}
в двоичной с.с. – алфавит {0, 1}
в 16-ричной с.с. – алфавит {0, 1, …, 9, A, B, C, D, E, F}
(вместо 10,11,12,13,14,15)
2. Любое число из заданного диапазона должно быть представимо алфавитом
3. Каждое число должно быть представимо единственным набором символов
4. С.с. должна быть пригодной и удобной (экономичной) для работы с заданной
арифметикой.
Таким образом, требования к с.с. можно записать кратко в виде кортежа требований:
{Требования}:= {алфавит, представимость, единственность, экономичность}

5.

Понятия и алгоритмы, связанные с позиционной системой счисления
1. Символы в условной записи числа нумеруются начиная с правого разряда. Его номер –
нуль. Остальные разряды нумеруются по возрастанию.
Пример:
Число 1024 в десятичной с.с. записывают так: 102410
Если номер старшего разряда = m, то общее число
символов в условной записи числа = m + 1
Разряд №0
Разряд №1
Разряд №2
Разряд №3
2. Основание (база) q – количество символов в алфавите данной с.с.; q – обычно целое
положительное число.
Пример:
В десятичной с.с. q = 10, в двоичной с.с. q = 2
3. Основание используется для расшифровки значения числа:
Пример:
102410 Расшифровка: 1 103 + 0 102 + 2 101 + 4 100
Номера разрядов: 3 2 1 0
= 1000 + 20 + 4 = 102410

6.

4. Перевод числа из с.с. с основанием q в десятичную с.с.
В общем случае число A с основанием q (Aq), представленное условной записью из (m + 1)
символов (Aq = am am-1 … a0), расшифровывается по степеням q следующим образом:
m
Aq a i q i
i 0
Пример 1: Основание с.с. q = 2
Требуется расшифровать (т.е. прочесть как
десятичное) число 100112
А). Подписываем под каждым символом номер разряда, начиная справа, с нуля:
Aq = 1 0 0 1 1
43210
Б). Возводим основание в степень, соответствующую номеру разряда, и суммируем.
Получаем результат в 10-чной с.с.
1·24 + 0·23 + 0·22 + 1·21 + 1·20 = 16+2+1=1910
Пример 2: Основание с.с. q = 3
Алфавит? {0; 1; 2}
Переведите в 10-чную с.с. число 1023
Ответ: 1110

7.

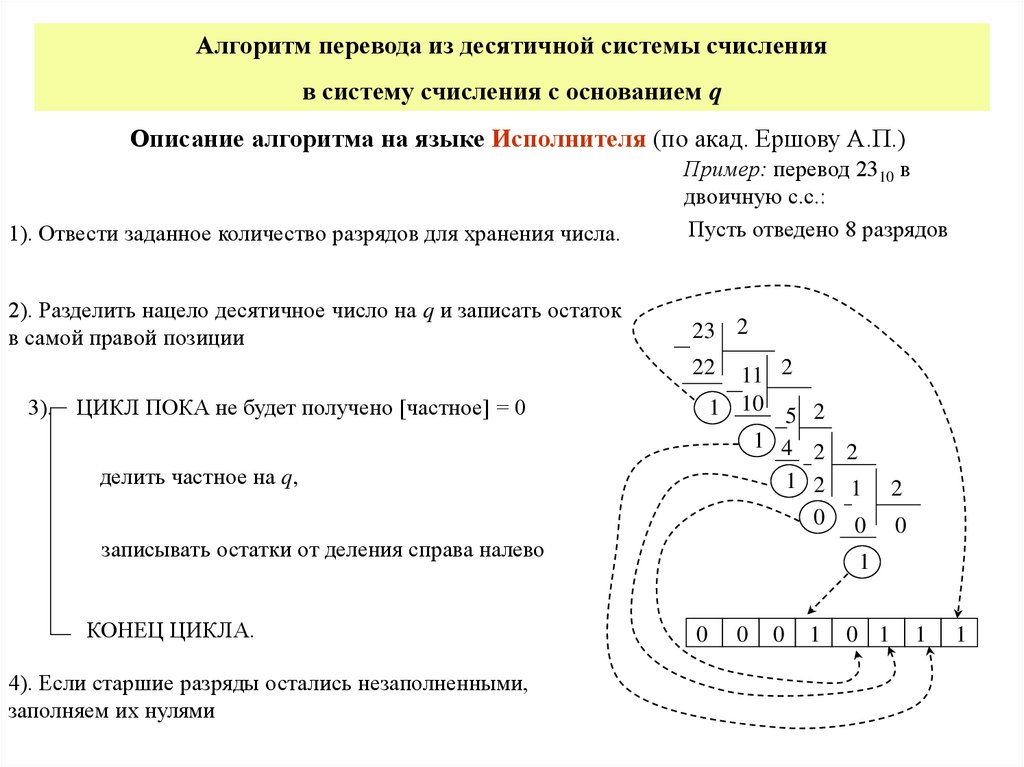
Алгоритм перевода из десятичной системы счисления
в систему счисления с основанием q
Описание алгоритма на языке Исполнителя (по акад. Ершову А.П.)
1). Отвести заданное количество разрядов для хранения числа.
Пример: перевод 2310 в
двоичную с.с.:
Пусть отведено 8 разрядов
2). Разделить нацело десятичное число на q и записать остаток
в самой правой позиции
23 2
22
3).
11 2
1 10 5 2
1 4
2 2
1 2 1
0 0
ЦИКЛ ПОКА не будет получено [частное] = 0
делить частное на q,
записывать остатки от деления справа налево
КОНЕЦ ЦИКЛА.
4). Если старшие разряды остались незаполненными,
заполняем их нулями
2
0
1
0
0
0
1
0 1
1
1

8.

Проверка: 2310 = 101112 =
1·24 + 0·23 + 1·22 + 1·21 + 1·20 = 16 + 4 + 2 + 1 = 2310
Аналогично переводится число из 10-чной в произвольную с.с
Пример: перевести 2310 в 5-ную с.с.
23
20
3
Алфавит?
5
Проверка:
4
5
0
2310 = 435 = 4·51 + 3·50 = 20 + 3 = 2310
0
4
0
0
0
0
0
0
{0; 1; 2; 3; 4}
4
3
Задача: перевести 23 в 24-ную с.с.

9.

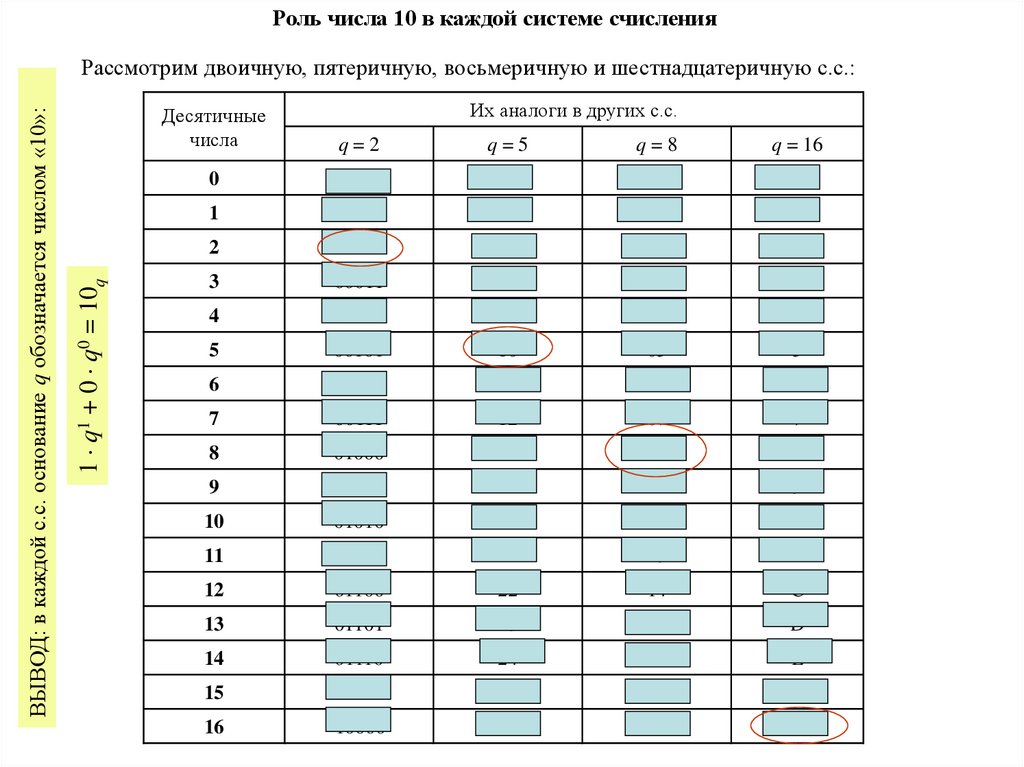
Роль числа 10 в каждой системе счисления
1 q1 + 0 q0 = 10q
ВЫВОД: в каждой с.с. основание q обозначается числом «10»:
Рассмотрим двоичную, пятеричную, восьмеричную и шестнадцатеричную с.с.:
Их аналоги в других с.с.
Десятичные
числа
q=2
q=5
q=8
q = 16
0
00000
00
00
0
1
0001
01
01
1
2
00010
02
02
2
3
00011
03
03
3
4
00100
04
04
4
5
00101
10
05
5
6
00110
11
06
6
7
00111
12
07
7
8
01000
13
10
8
9
01001
14
11
9
10
01010
20
12
A
11
01011
21
13
B
12
01100
22
14
C
13
01101
23
15
D
14
01110
24
16
E
15
01111
30
17
F
16
10000
31
20
10

10.

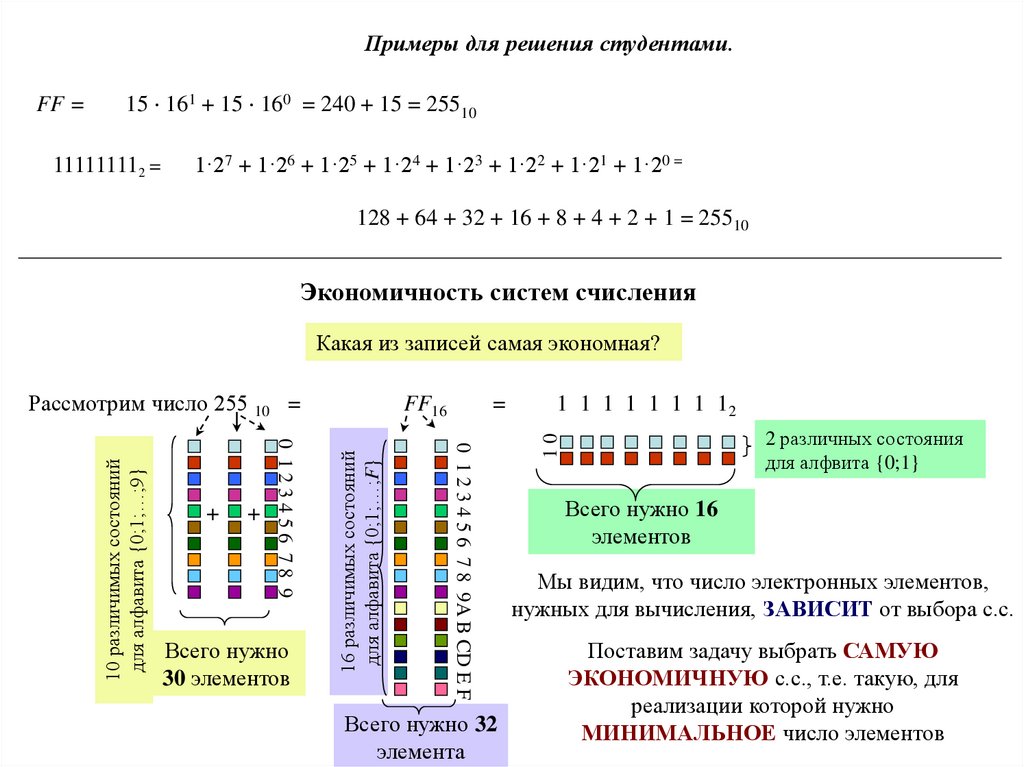
Примеры для решения студентами.
FF =
15 161 + 15 160 = 240 + 15 = 25510
111111112 =
1·27 + 1·26 + 1·25 + 1·24 + 1·23 + 1·22 + 1·21 + 1·20 =
128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 25510
Экономичность систем счисления
Какая из записей самая экономная?
Всего нужно
30 элементов
=
Всего нужно 32
элемента
1 1 1 1 1 1 1 12
2 различных состояния
для алфвита {0;1}
10
16 различимых состояний
для алфавита {0;1;…;F}
+
FF16
0 1 2 3 4 5 6 7 8 9A B CD E F
+
0 123456 78 9
10 различимых состояний
для алфавита {0;1;…;9}
Рассмотрим число 255 10 =
Всего нужно 16
элементов
Мы видим, что число электронных элементов,
нужных для вычисления, ЗАВИСИТ от выбора с.с.
Поставим задачу выбрать САМУЮ
ЭКОНОМИЧНУЮ с.с., т.е. такую, для
реализации которой нужно
МИНИМАЛЬНОЕ число элементов

11.

Для решения задачи нужно:
А). Рассчитать зависимость числа элементов от основания с.с.
Б). Судя по рассмотренному примеру, такая зависимость должна иметь минимум.
В). Для нахождения минимума взять производную, приравнять ее нулю и найти аргумент (в данном
случае – основание с.с.), соответствующий нулю производной – т.е. точке минимума.
Выкладки
1). Пусть известно число разрядов N. Какое максимальное число Amax можно записать, используя такое
число разрядов?
Получается, что в каждом
F
1 1 1 1
F F F
разряде – на 1 меньше
9 9 9 9
основания с.с.
2-чная с.с.
16-чная с.с.
10-чная с.с.
Поэтому для ПРОИЗВОЛЬНОЙ с.с
с основанием q запишем:
q-1
q-1
…
q-1
N-1
N–2
…
0
Подсчитаем значение вписанного в таблицу числа:
Amax q 1 q
N 1
q 1 q
N 2
Amax
... q 1 q q 1 q
= qN 1
0
N 1
q
N 2
q0 1 q N
... q q 1
1 q
0
сумма первых N
членов
q0 1 q N
геометрической
q 1
прогрессии
q 1
q 1
N

12.

2). На примерах мы убедились, что электронные элементы должны иметь столько устойчивых
состояний, сколько символов в алфавите
Поэтому будем оценивать затраты на электронные элементы для представления числа по числу
устойчивых состояний.
C=N·q
3).Введем показатель экономичности с.с.
Число разрядов
Основание с.с
Тогда появляется инструмент для сравнения разных с.с. по числу элементарных (т.е. устойчивых)
состояний, нужных для представления числа.
4). Пусть нужно представить число Amax в разных с.с. и выбрать наиболее экономичную.
Из равенства Amax = qN – 1 найдем N.
Логарифмируем по основанию q:
qN = Amax + 1
N · logqq = logq(Amax+1).
=1
5). Получим формулу для показателя экономичности:
C=N·q
=
q·logq(Amax+1)
N = logq(Amax+1)

13.

5). Получим формулу для показателя экономичности:
C=N·q
=
q·logq(Amax+1)
6). Используем эту формулу для сопоставления с.с. с любым основанием с двоичной с.с.
Для этого введем ОТНОСИТЕЛЬНЫЙ ПОКАЗАТЕЛЬ ЭКОНОМИЧНОСТИ H, принимая
экономично сто двоичной с.с. за единицу:
число элементов в с.с. с основанием q q·logq Amax 1
H
число элементов в с.с. с основанием 2 2·log2 Amax 1
7). Упростим это выражение, используя формулу:
log q a
ln a
ln q
(натуральные логарифмы, основание = e = 2.718281828…)
Получим:
q ln Amax 1
ln 2
ln 2 q
H
.
2
ln q
ln Amax 1 2 ln q
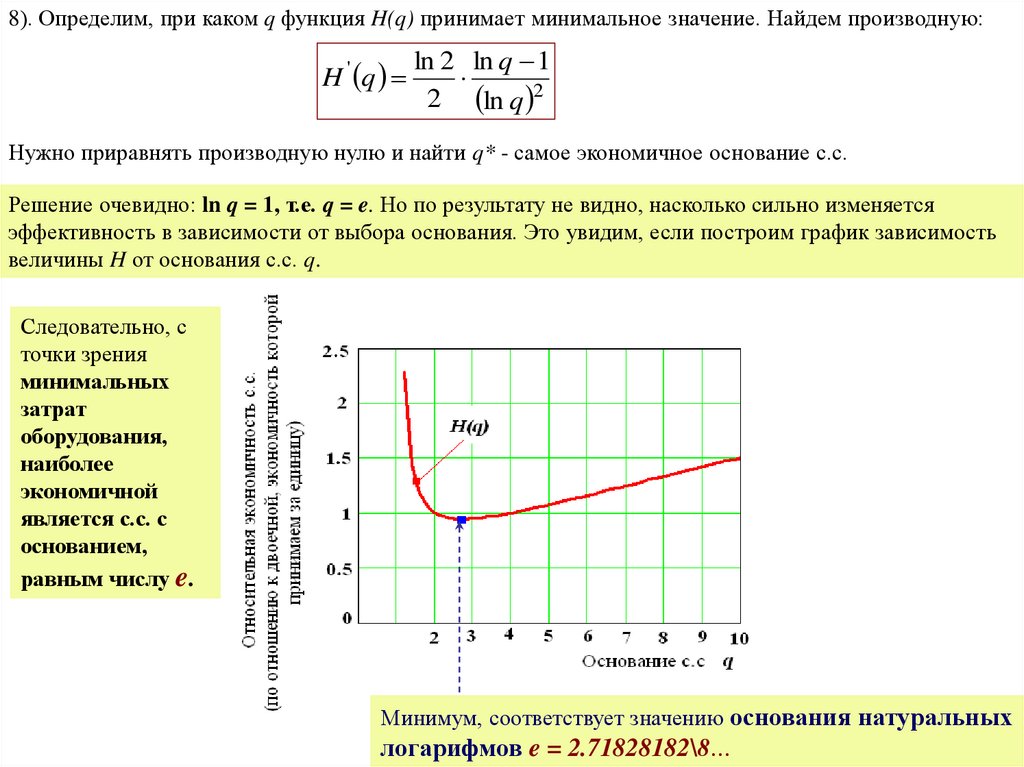
8). Определим, при каком q функция H(q) принимает минимальное значение. Найдем производную:
H ' q
ln 2 ln q 1
2 ln q 2

14.

8). Определим, при каком q функция H(q) принимает минимальное значение. Найдем производную:
H ' q
ln 2 ln q 1
2 ln q 2
Нужно приравнять производную нулю и найти q* - самое экономичное основание с.с.
Решение очевидно: ln q = 1, т.е. q = e. Но по результату не видно, насколько сильно изменяется
эффективность в зависимости от выбора основания. Это увидим, если построим график зависимость
величины H от основания с.с. q.
Следовательно, с
точки зрения
минимальных
затрат
оборудования,
наиболее
экономичной
является с.с. с
основанием,
равным числу e.
Минимум, соответствует значению основания натуральных
логарифмов e = 2.71828182\8…

15.

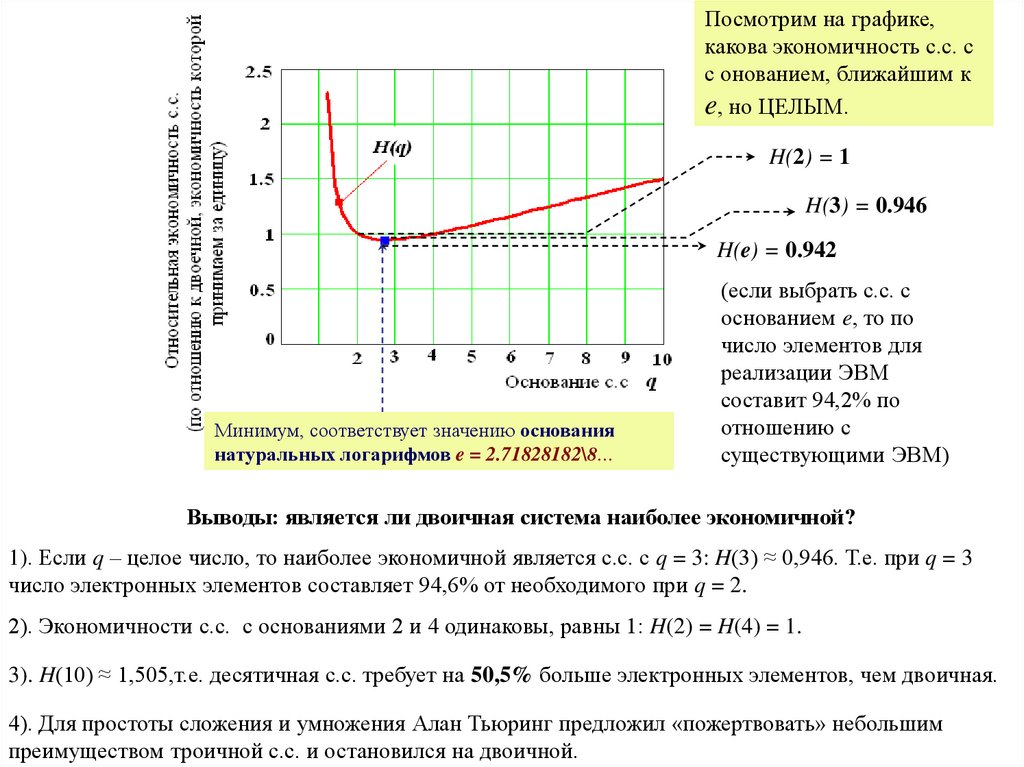
Посмотрим на графике,
какова экономичность с.с. с
с онованием, ближайшим к
e, но ЦЕЛЫМ.
H(2) = 1
H(3) = 0.946
H(e) = 0.942
Минимум, соответствует значению основания
натуральных логарифмов e = 2.71828182\8…
(если выбрать с.с. с
основанием e, то по
число элементов для
реализации ЭВМ
составит 94,2% по
отношению с
существующими ЭВМ)
Выводы: является ли двоичная система наиболее экономичной?
1). Если q – целое число, то наиболее экономичной является с.с. с q = 3: H(3) ≈ 0,946. Т.е. при q = 3
число электронных элементов составляет 94,6% от необходимого при q = 2.
2). Экономичности с.с. с основаниями 2 и 4 одинаковы, равны 1: H(2) = H(4) = 1.
3). H(10) ≈ 1,505,т.е. десятичная с.с. требует на 50,5% больше электронных элементов, чем двоичная.
4). Для простоты сложения и умножения Алан Тьюринг предложил «пожертвовать» небольшим
преимуществом троичной с.с. и остановился на двоичной.