Similar presentations:
Основные понятия теории множеств. Лекция №9
1.
ЛЕКЦИЯ №9Основные понятия теории
множеств
2.
План1. Общие понятия и определения теории
множеств.
2. Способы задания множеств.
3. Подмножества. Равенство множеств.
3.
Объектом исследования дискретнойматематики
являются
дискретные
множества – совокупность, набор
некоторых элементов. Простейшие
представления о множествах появились
в связи с исследованиями в области
карточных игр и возникновением
комбинаторики и дискретной теории
вероятностей.
4.
В этом разделе мы систематизируемимеющиеся из курса элементарной
математики
представления
об
универсальном языке теории множеств,
познакомимся с видами множеств и
отношений между ними, узнаем, как
сравнивать конечные и бесконечные
множества и как подсчитывать число их
элементов.
5.
Сегодня мы знаем, что,логически говоря, возможно
вывести почти всю современную
математику из единого источника – теории множеств.
Николя Бурбаки
6.
Понятиемножества,
было
введено
в
математику создателем
теории
множеств
немецким
ученым
Георгом
Кантором
(1845–1918).
7.
«Множество –объединение в одно
целое объектов,
хорошо различимых
нашей интуицией или
нашей мыслью».
Георг Кантор
8.
Множество (по Кантору) – совокупностьобъектов
произвольной
природы,
которая
рассматривается как единое целое.
Объекты, входящие в
называются его элементами.
состав
множества,
Примерами множеств могут служить множество
всех книг, составляющих данную библиотеку;
множество всех точек данной линии; множество всех
решений данного уравнения; множество всех
одноклеточных организмов и т.п.
9.
1.1. Замените по смыслу словосочетаниясо словом «множество» одним словом:
множество птиц;
множество людей в поезде;
множество футболистов;
множество артистов в театре.
10.
Такое описание понятия множестванельзя считать логическим определением, а
всего лишь пояснением. Понятие множества
принимается как исходное, первичное, то
есть не сводимое к другим понятиям и
является
базисным
неопределяемым
понятием, на котором строится теория
множеств.
11.
Множества принято обозначать прописнымибуквами латинского алфавита: A, B, C, …
Элементы
множества
будем
обозначать
строчными латинскими буквами: a, b, c, …
Предложения вида «объект a есть элемент
множества A», «объект a принадлежит множеству
A», имеющие один и тот же смысл, кратко
записывают в виде a A . Если элемент a не
принадлежит множеству A, то пишут a A .
Символ называется знаком принадлежности.
12.
1.2. Принадлежит ли:число 2 множеству простых чисел;
число 13 множеству чисел, кратных 4;
число 2 множеству рациональных
чисел;
месяц январь множеству зимних
месяцев;
Аргентина множеству стран Европы;
группа 1П-20 множеству групп
отделения информационных
технологий и экономики.
13.
1.3. Множество А состоит из двухшариковых ручек. Из одной ручки
достанем стержень. Является ли он
элементом множества А? Объясните
ответ.
14.
Множество, содержащее определенноечисло элементов, называется конечным.
В
противном
случае
множество
называется бесконечным.
Например, множество всех дней
недели
конечно
(содержит
семь
элементов), а множество всех точек
прямой бесконечно.
15.
1.4. Определите, какие из множествявляются конечными:
множество планет Солнечной
системы;
множество действительных чисел;
множество одноклеточных
организмов;
множество континентов;
множество летающих крокодилов.
16.
Рассматривают в математике и множество,не содержащее ни одного элемента.
Определение 1. Множество, не содержащее ни одного элемента, называется пустым
множеством и обозначается символом .
Так, к примеру, множество действительных
корней уравнения x 2 4 x 5 0 является пустым.
17.
Определение 2.Множество, состоящее из
всех возможных элементов, обладающих данным
признаком,
называется
универсальным
множеством, или универсумом. Обозначается U.
Так, например множество всех студентов,
обучающихся в конкретной группе, является
универсальным, при этом множество студентов,
присутствующих на данном занятии, универсальным
считать нельзя.
Множество U всех планет Солнечной системы
также является универсальным множеством.
18.
Элементами множества могут быть множества.Например, можно говорить о множестве групп
колледжа. Элементы этого множества – группы,
являющиеся в свою очередь множествами
студентов. Но конкретный студент одной из групп
уже не является элементом множества групп
колледжа.
Определение 3. Множество,
элементами
которого являются другие множества, называется
семейством (классом).
19.
Определение 4. Число элементов конечного множества называется его мощностью.Если множество A содержит n элементов, то
будем писать A n .
Если A , то A 0 .
Мощность
бесконечного
множества
является более сложным понятием. Оно будет
рассмотрено далее.
20.
1.5. Укажите мощность следующихмножеств:
множество месяцев в году;
множество игроков футбольной команды;
множество групп специальности
«Компьютерные системы и комплексы»;
множество говорящих рыб;
множество положительных корней
3
2
уравнения x 4 x 5x 0 .
21.
Множество считают заданным, если олюбом объекте можно сказать, принадлежит
он этому множеству или не принадлежит.
Множество можно задать следующими
способами:
1) перечислением всех его элементов
(списком);
2) характеристическим
свойством
элементов множества;
3) порождающей процедурой.
22.
Первый способ задания множеств применим, какправило, только для конечных множеств, да и то при
условии, что число элементов множества невелико. Если
a,b,c,d – обозначения различных объектов, то множество
A этих объектов записывают так: A={a;b;c;d}.
Запись читают: «A – множество, элементы которого
a, b, c, d».
Порядок перечисления элементов множества не
имеет значения. Так, множества {a; b; c; d} и {b; c; d; a}
совпадают.
Например, определим множество планет Солнечной
системы: А={Земля, Марс, Венера, Юпитер, Сатурн,
Уран, Меркурий, Нептун}.
23.
1.6. Задайте списком следующие множества:множество дней недели;
множеств букв русского алфавита,
которые обозначают гласные звуки;
множество знаков арифметических
действий;
множество мастеров спорта, которые
учатся в вашей группе;
множество чисел, которые в сумме с
числом 4 дают число 4.
24.
Вторым способом можно задавать как конечные,так и бесконечные множества.
Характеристическое свойство – это такое
свойство, которым обладает каждый элемент,
принадлежащий множеству, и не обладает ни один
элемент, который ему не принадлежит. Обозначив
символом P(x) характеристическое свойство
элементов множества A, будем писать: A = {x| P(x)}.
Например, запись M n | n N , n 5 обозначает
множество натуральных чисел, меньших пяти, т.е.
М={1;2;3;4}.
25.
1.7. Определите элементы множества,заданного характеристическим
свойством:
A x | x Z , 2 x 2 ;
A x | x R, x 3 3 x 2 2 x 0 ;
A x | x N , x 3 3 x 2 2 x 0 ;
2
2
M x; y | x, y R, x y 1 .
26.
1.8. Задайте с помощьюхарактеристического свойства
множество A 1,11,21,31,41,...
A x | x N , x 10n 1, n 0;1;....
27.
1.8. Задайте с помощьюхарактеристического свойства
множество A 1 ; 2 ; 3 ;...; 99
100
2 3 4
n
A x | x Q, x
, n 1;2;...;99
n 1
1
A x | x Q, x 1 , n 2;3;...;100
n
28.
Порождающая процедура описывает способполучения элементов нового множества из уже
полученных элементов или из других объектов.
Тогда элементами множества считаются все
объекты, которые могут быть получены с помощью
этой процедуры. С помощью порождающей
процедуры можно задавать множества, содержащие
любое число элементов.
Например, множество М ={1;2;4;8;16;32;..} всех
чисел, являющихся неотрицательными степенями
числа 2, можно задать с помощью порождающей
процедуры по правилам:
1. 1 М ; 2. если k М , то 2k М .
29.
Пример 1. Определим различными способамимножество М всех нечетных чисел, не превышающих 10:
1) М = {1, 3, 5, 7, 9};
2) М x | x N , x 2k 1, k N , k 5 ;
3) порождающая процедура определяется
правилами:
1 М ; если k М , то k 2 М , k 7 .
30.
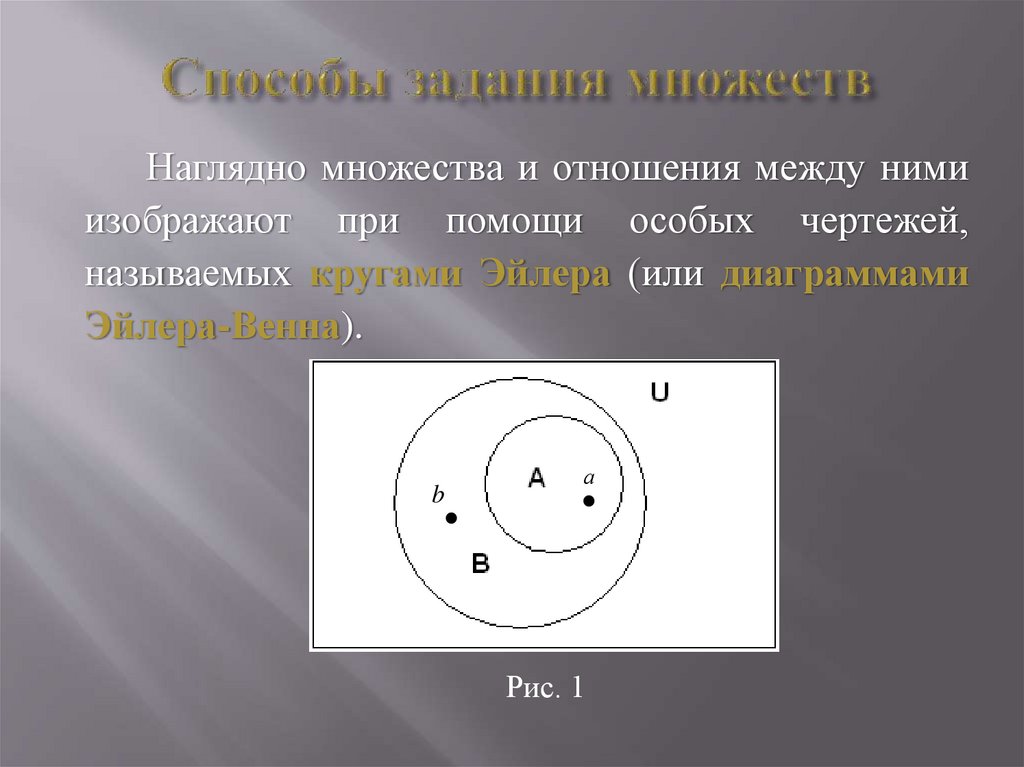
Наглядно множества и отношения между нимиизображают при помощи особых чертежей,
называемых кругами Эйлера (или диаграммами
Эйлера-Венна).
b
а
Рис. 1
31.
bа
Так, на диаграмме на
рис.
1
изображены
множества A, B,
и
универсальное множество
U.
При этом универсальные множества на диаграммах
Эйлера-Венна, как правило, изображаются в виде
прямоугольников.
Элементы множеств изображаются на диаграммах
Эйлера-Венна точками.
Так, на рис. 1, a A , a B , a U , при этом
b A , b B , b U .
32.
Определение 5. Множество B называетсяподмножеством множества A, если каждый элемент
множества
B
принадлежит
множеству
A.
Обозначается В А . Символ называется знаком
включения.
Таким образом, В А , если для любого х
x B x A .
Если множество B является подмножеством
множества A, то говорят также, что B содержится в A
или B включено в A.
33.
Пример 2. ПустьА={a, b, c, d, e, f, g, h, i, j, k},
B={c, e, g, h, j, k}.
Множество
В
является
подмножеством множества А, поскольку
каждый
элемент
множества
В
принадлежит множеству А.
34.
1.9. Назовите любые три подмножества:множества нот музыкальной октавы;
множества треугольников на плоскости;
множества месяцев в году.
35.
1.10. Образует ли множество В подмножествомножества А, если:
В – множество равнобедренных
треугольников, А – множество
равносторонних треугольников;
В – множество чисел, которые делятся на 10,
А – множество чисел, которые делятся на 5;
В – множество студентов группы
специальности «Компьютерные системы и
комплексы», А – множество академических
групп отделения информационных
технологий и экономики.
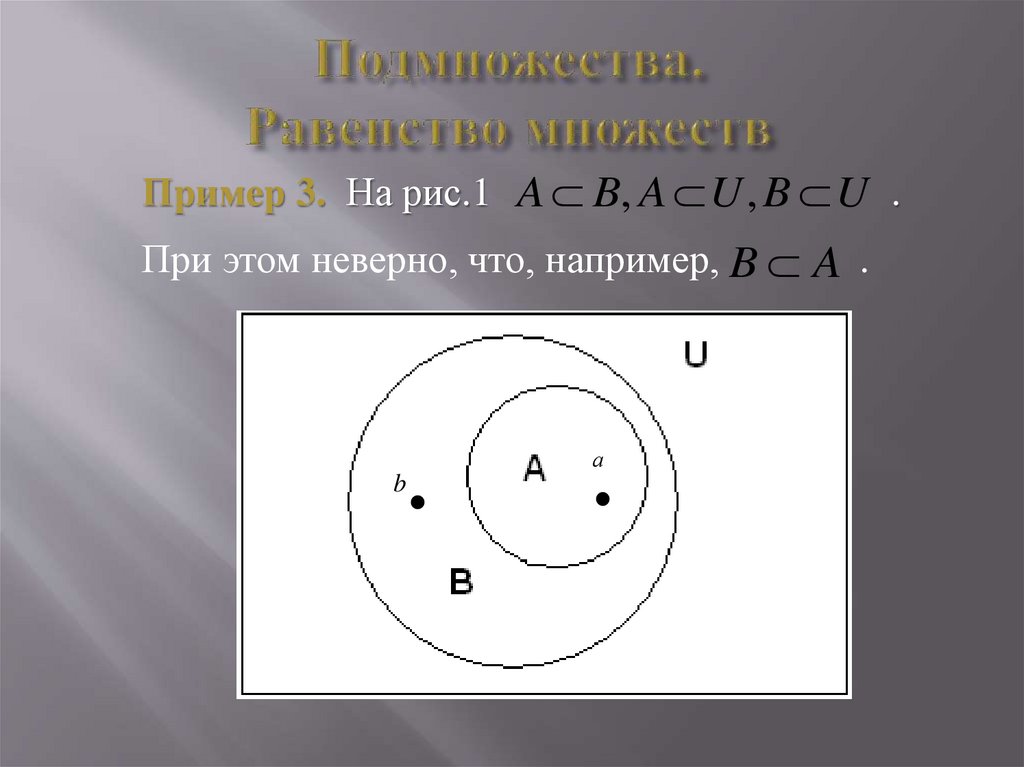
36.
Пример 3. На рис.1 A B, A U , B U .При этом неверно, что, например, B A .
а
b
37.
Пример 4. Для известных числовых множествнатуральных чисел N, целых чисел Z, рациональных
чисел Q, действительных чисел R, комплексных
чисел C очевидны включения N Z Q R C
(рис. 2).
N
Z
Q
R
C
38.
1.11. Составьте цепочки включений так,чтобы каждое последующее множество
содержало предыдущее:
А – множество всех трапеций;
В – множество всех прямоугольников;
С – множество всех четырехугольников;
D – множество всех квадратов;
Е – множество всех параллелограммов;
F – множество всех многоугольников.
39.
Согласно данному определению подмножествакаждое множество является подмножеством самого
себя: A A .
Кроме того, считается, что пустое множество есть
подмножество любого множества A: A .
Различают два вида подмножеств множества А.
Само множество А и называются несобственными
подмножествами множества А.
Любые подмножества множества А, отличные от А и
, называются собственными подмножествами
множества А.
40.
Определение 6. Множество всех подмножествмножества A называется его булеаном (или
множеством-степенью) и обозначается через P(A)
А
2
(или
).
Пример 5. Если A = {a, b, c}, то
P(A) = { , {a},{b},{c},{a, b},{b, c}, {a, c},{a, b, c}}.
41.
Обратим внимание, что для множеств необходимоучитывать различие в использовании знаков включения
и принадлежности .
Пример 6. Пусть М – множество академических
групп колледжа, а Р – группа 1П-20. Хотя Р само
является множеством (состоит из студентов группы 1П20), верна запись Р М , так как группа Р является
элементом множества М всех групп колледжа.
Запись Р М неверна, т.к. множества Р и М содержат разные элементы: Р – людей, а М – групп. Однако,
если рассмотрим множество K всех студентов колледжа,
то тогда верной является запись Р K .
42.
1.12. Вместо знака _ вставьте знаки так,чтобы получились истинные
высказывания:
_R
3
_ 4;3
2
_ 2;6
4;3 __
2;6
2;6
1;4 __
__ 1;1
43.
1.13. Вместо знака _ вставьте знаки так,чтобы получились истинные
высказывания:
a
_ a; b
_ a; b
a
__ a; b
a
a _ a ; b
_ a; b , b; c , a; c
a; b
_
44.
Определение 7. Множества A и B называютсяравными, если они состоят из одних и тех же элементов.
Обозначают: А = В.
Например, равными являются множества решений
х 2
, 5 х 3 125, так как их
уравнений, 4 х 8 16,
15 5
решением является одно и то же число 6.
Равными являются множества букв, из которых
состоят слова «НАВЕС» и «ВЕСНА».
2
х
1 и
Равны множество корней уравнения
множество М 1 k , k 0;1;2;... .
45.
Справедливо следующее утверждение, котороетакже можно рассматривать в качестве определения
равных множеств.
Теорема 1.
A B A Bи
B A.
Из теоремы 1 вытекает способ доказательства
равенства двух множеств: если доказать, что каждый
элемент из множества A является элементом
множества B и, наоборот, каждый элемент из
множества B является элементом множества A, то
делают вывод, что А = В.











































 mathematics
mathematics








