Расстояние между скрещивающимися прямыми

1.   «Расстояние между скрещивающимися прямыми»  

2.

M
M
M
M
M
M
b
h
b h b
h
h
h
h
h
h
h
aa
a
a
a
a
M
M
MM
b
h
MM
h b h hb
hb b
b
hb h b
Mh ha M b
M
a
h
h
h
h
h
h
ah a
a
a
h
h
MM
h h
M
h b b
b
h h
a
h
b b
a
ba
h
h h
a a
a

3. Теорема о Существовании общего перпендикуляра к двум скрещивающимся прямым

A
a
α
h
b
B
β

4.

5.

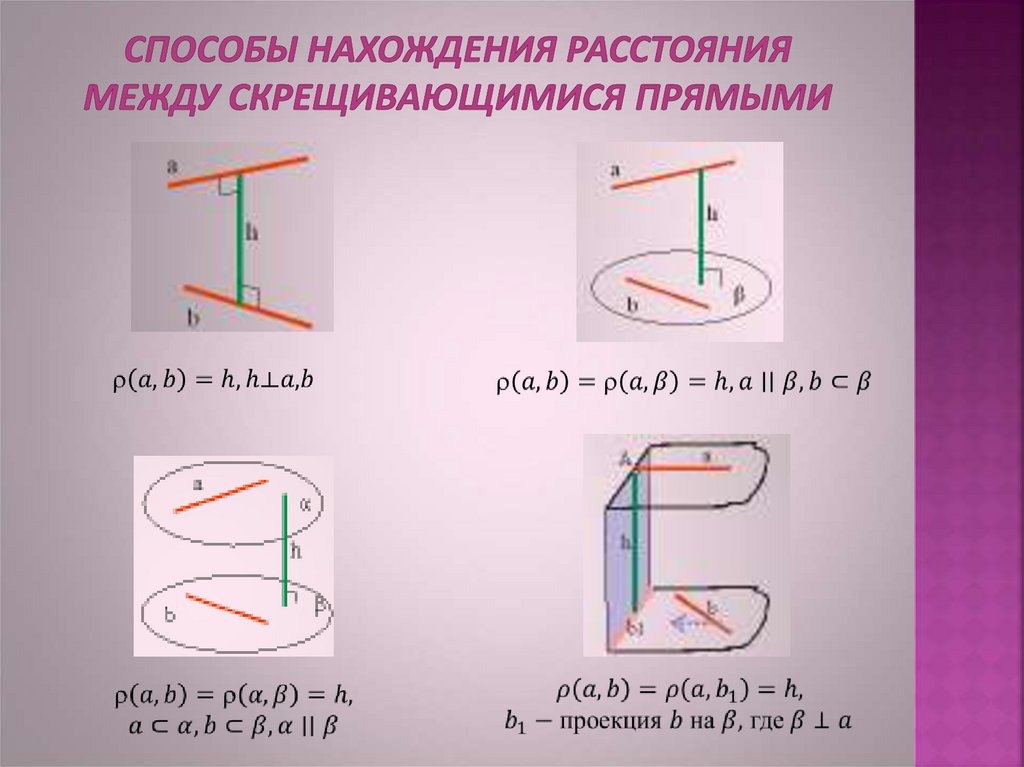
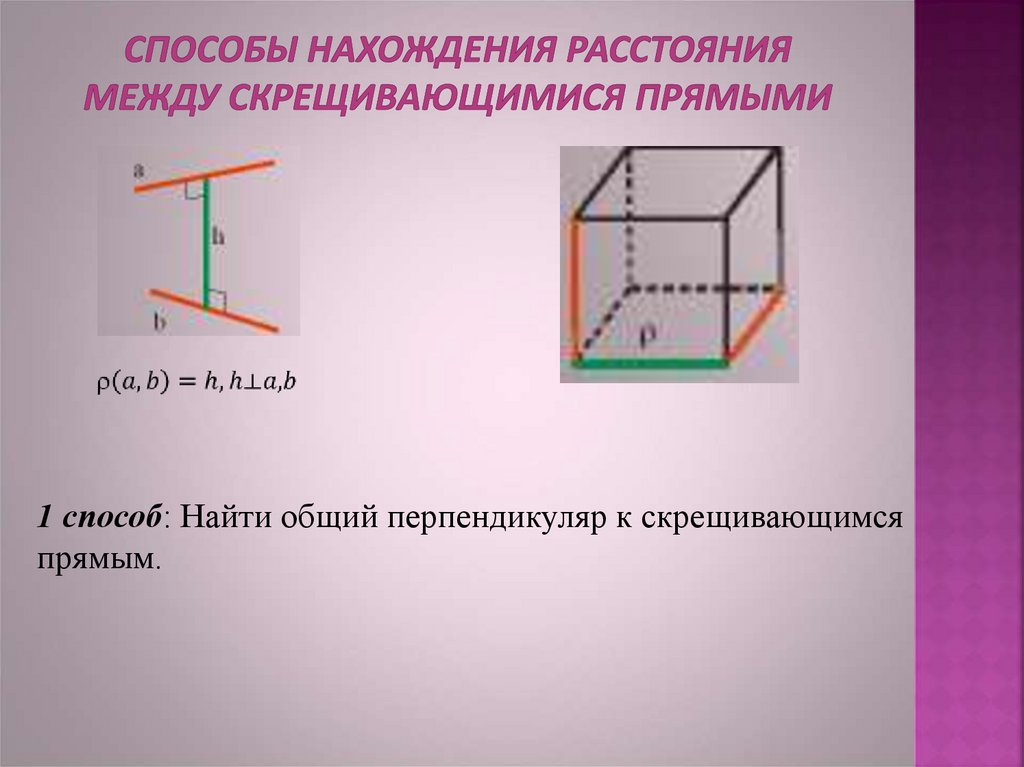
1 способ: Найти общий перпендикуляр к скрещивающимся
прямым.

6.

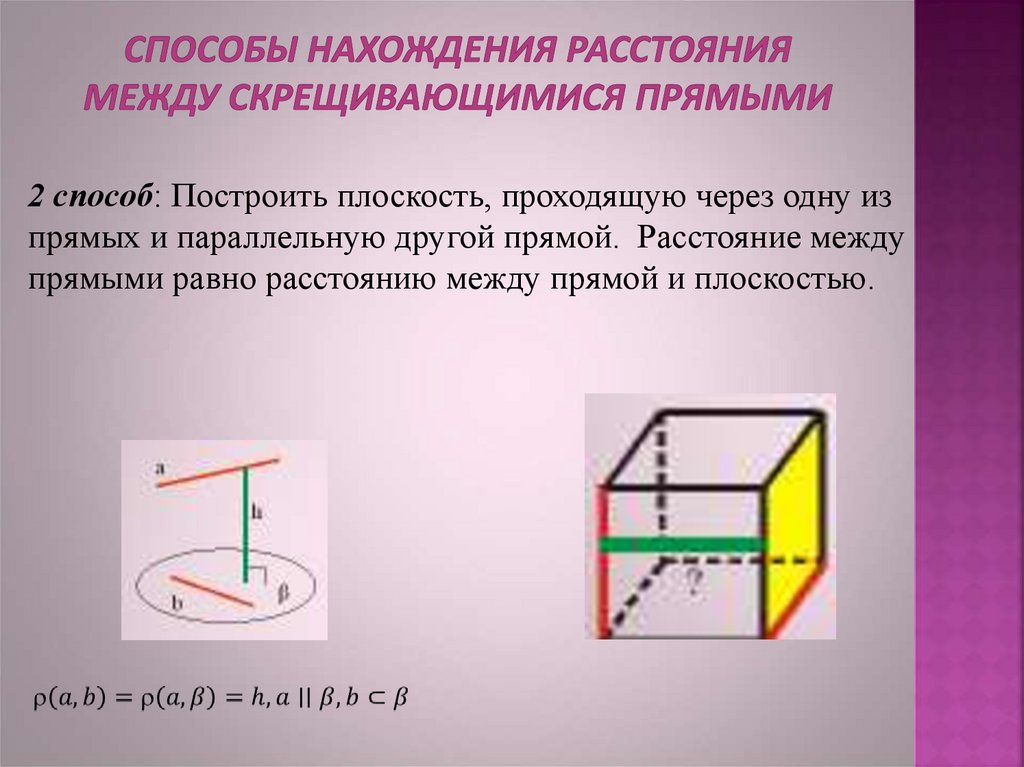
2 способ: Построить плоскость, проходящую через одну из
прямых и параллельную другой прямой. Расстояние между
прямыми равно расстоянию между прямой и плоскостью.

7.

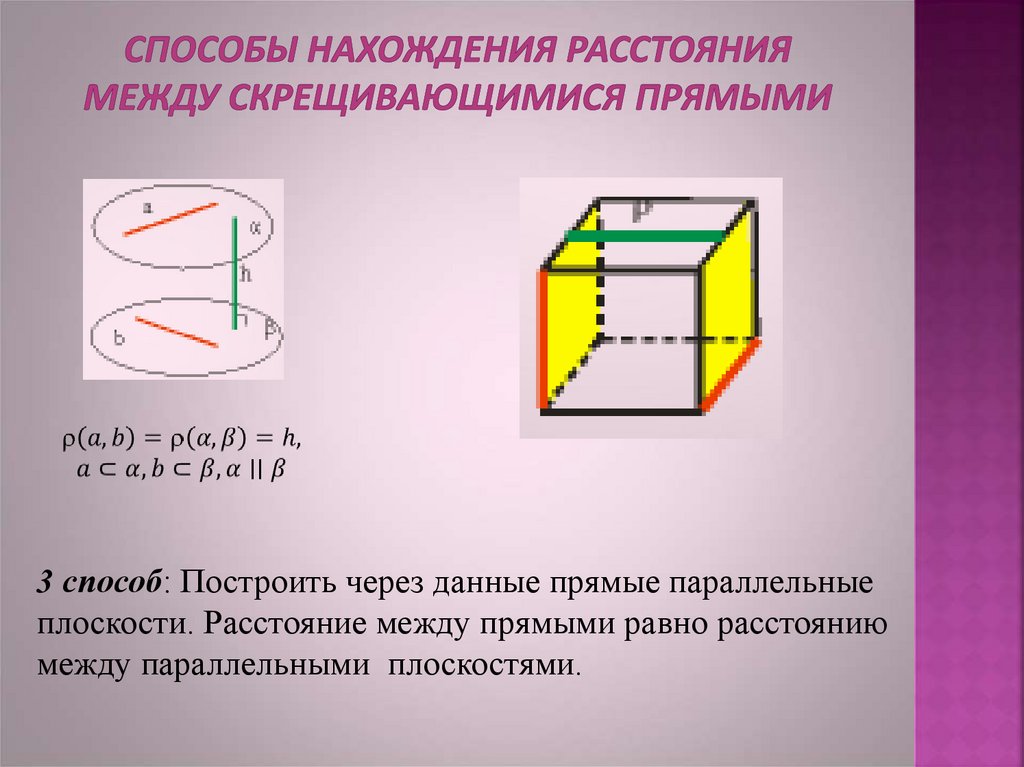
3 способ: Построить через данные прямые параллельные
плоскости. Расстояние между прямыми равно расстоянию
между параллельными плоскостями.

8.

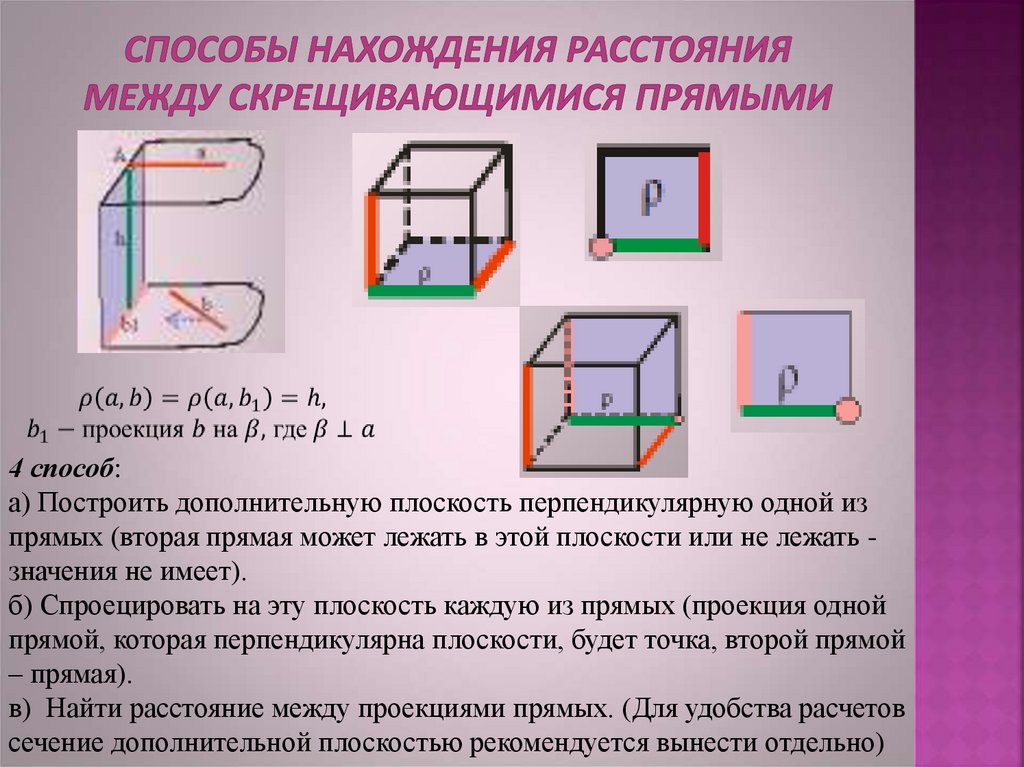
4 способ:
а) Построить дополнительную плоскость перпендикулярную одной из
прямых (вторая прямая может лежать в этой плоскости или не лежать значения не имеет).
б) Спроецировать на эту плоскость каждую из прямых (проекция одной
прямой, которая перпендикулярна плоскости, будет точка, второй прямой
– прямая).
в) Найти расстояние между проекциями прямых. (Для удобства расчетов
сечение дополнительной плоскостью рекомендуется вынести отдельно)

9. Способы нахождения расстояния между скрещивающимися прямыми

1 способ
2 способ
a
a
h
β
a
α
h
b
4 способ
A
a
h
b
3 способ
h
β
b
b
b1
ρ
ρ
ρ
ρ
?
ρ
ρ

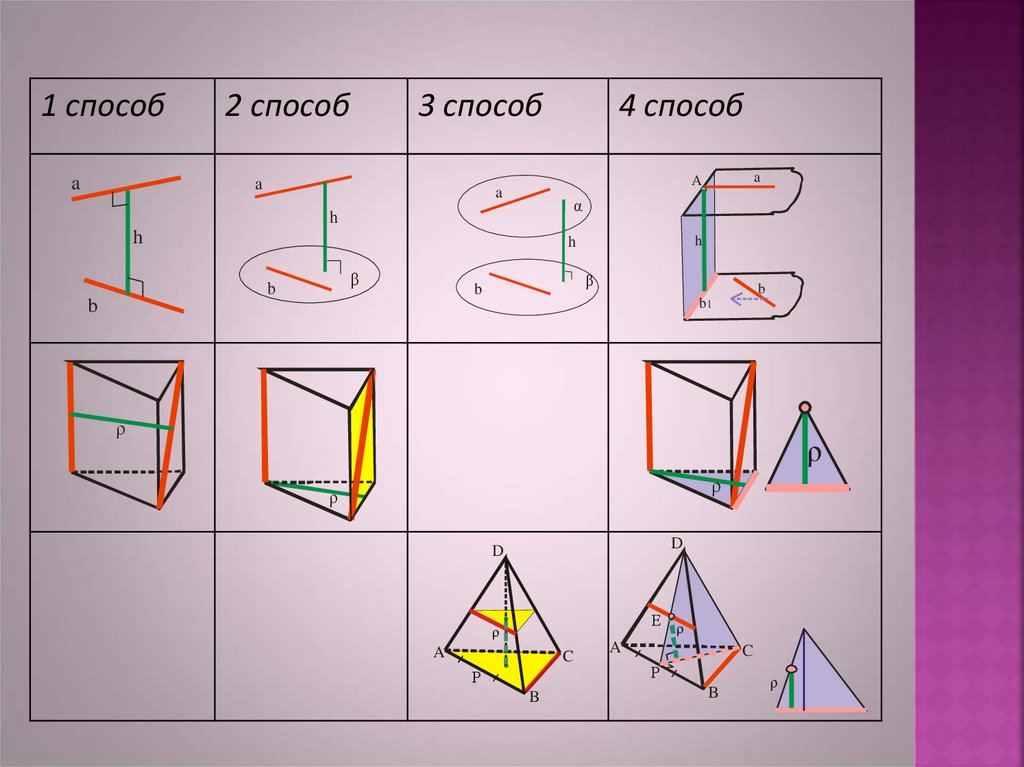
10. Способы нахождения расстояния между скрещивающимися прямыми

11.

1 способ
a
2 способ
3 способ
a
4 способ
α
h
h
h
h
β
b
a
A
a
β
b
b
b1
b
ρ
ρ
ρ
ρ
D
D
Е
A
C
Р
B
A
C
Р
B
ρ

12. задача 1

1 способ
2 способ
3 способ
a
a
a
α
h
b
b
B1
A1
D1
A
h
β
b
b
b1
B1
C1
A1
D1
B
C
D
β
B1
C1
B
A
a
A
h
h
A1
4 способ
D
A
A1
D1
B
C
B1
C1
D1
B
C
D
C1
A
C
D

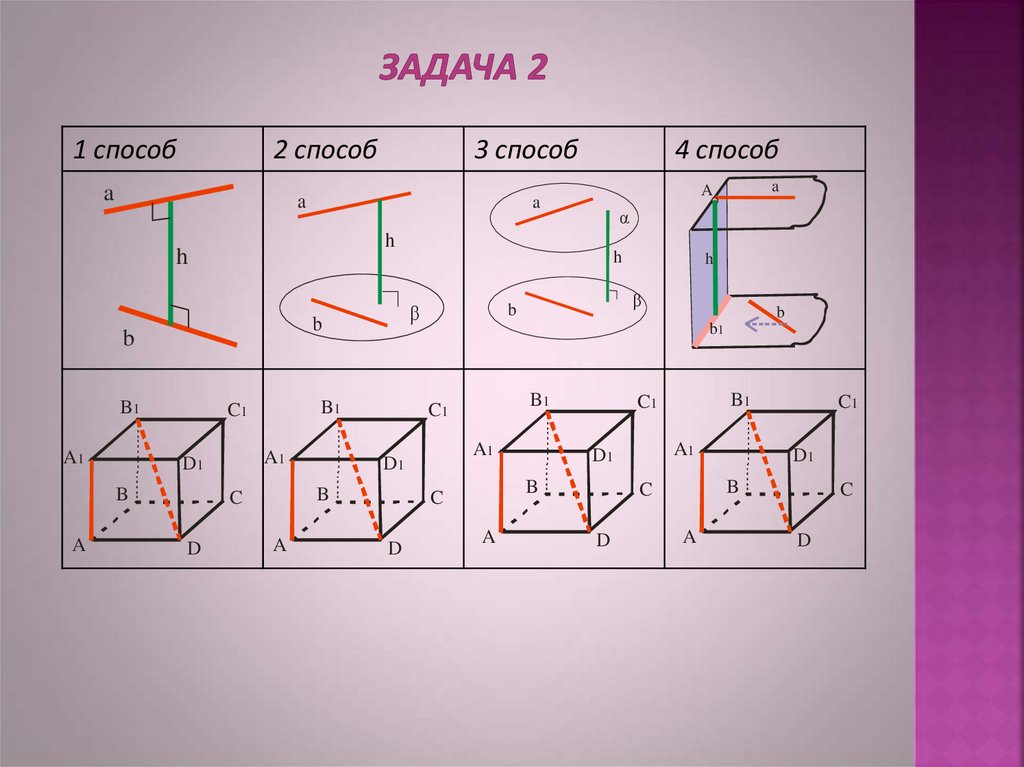
13. задача 2

1 способ
2 способ
a
a
b
A1
B1
C1
A1
D1
B
A
b
b1
B1
A1
D1
A
B1
C1
A1
D1
B
C
D
h
β
b
C1
B
C
D
α
h
β
a
A
h
b
B1
4 способ
a
h
A
3 способ
D1
B
C
D
C1
A
C
D

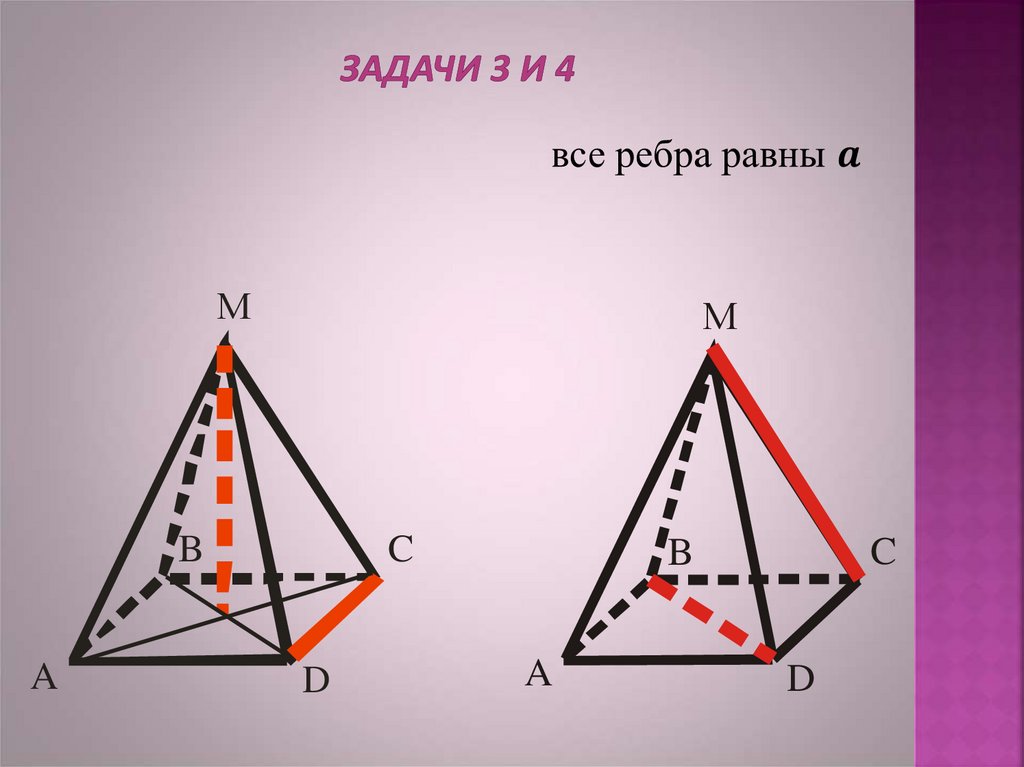
14. задачи 3 и 4

М
М
B
A
C
D
C
B
A
D

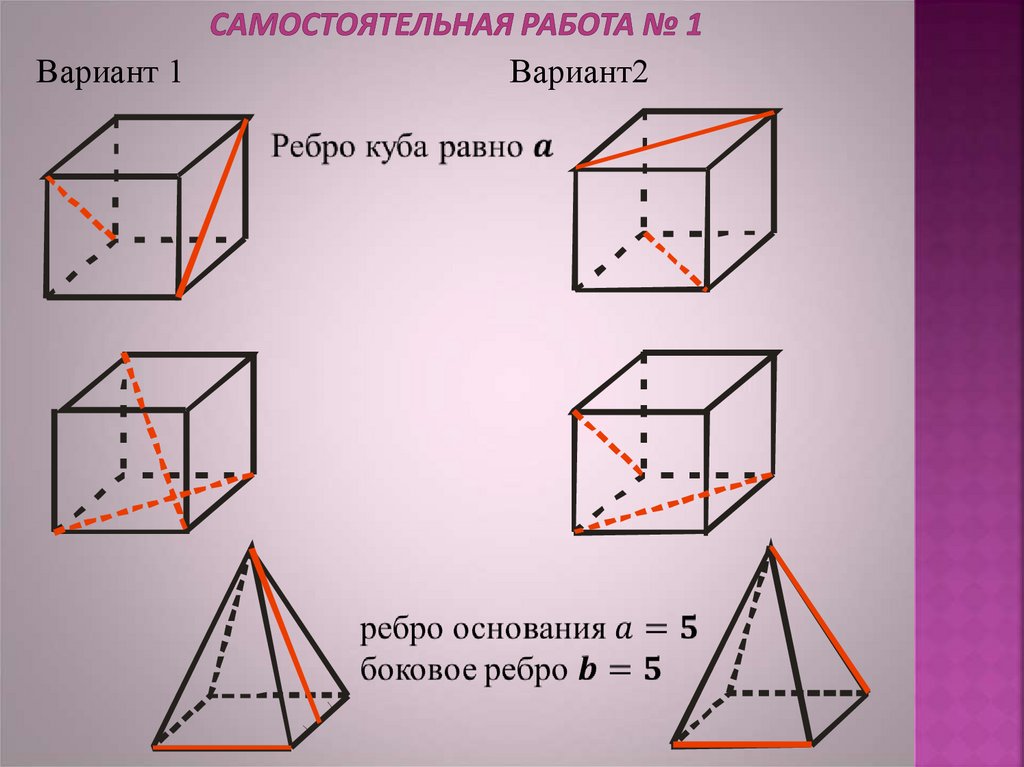
15. Самостоятельная работа № 1

Вариант 1
Вариант2

16. Самостоятельная работа N 2

Вариант 1
M
M
а
T
a
b
K
K
B
M
Куб со стороной равной а
М –середина ребра
а
C
a
30 град
A
A
D
KT||DC MT=TC
Правильная призма
Правильная пирамида,
все ребра равны а
B
а
C
АВС
прямоугольный,
АК АВС, В=90о,
С=30о, ВС=АК=а
Вариант 2
K
M
а
b
M
а
а
а
A
B
Куб со стороной равной а
М –середина ребра
Правильная призма
Правильная
пирамида, все ребра
равны а
а
АВС - правильный
АК АВС
АВ=а, АК=а
C

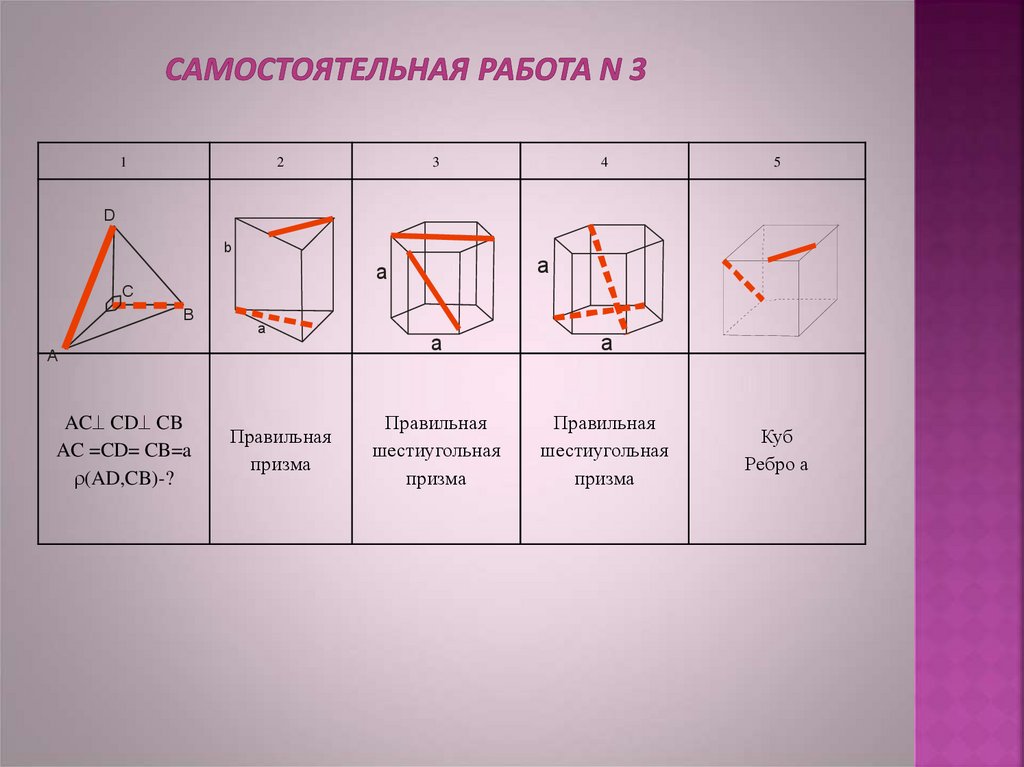
17. Самостоятельная работа N 3

1
2
3
4
5
D
b
а
а
С
В
a
А
AC CD CB
AC =CD= CB=a
(AD,CB)-?
Правильная
призма
а
а
Правильная
шестиугольная
призма
Правильная
шестиугольная
призма
Куб
Ребро а

18.

Практикум по теме: «Расстояние между скрещивающимися прямыми»
Алгоритм:
1 способ: Найти общий перпендикуляр к скрещивающимся прямым.
2 способ: Построить плоскость, проходящую через одну из прямых и параллельную другой прямой. Расстояние между прямыми
равно расстоянию между прямой и плоскостью.
3 способ: Построить через данные прямые параллельные плоскости. Расстояние между прямыми равно расстоянию между
Параллельными плоскостями.
4 способ: а) Построить дополнительную плоскость перпендикулярную одной из прямых (вторая прямая может лежать в этой
плоскости или не лежать - значения не имеет).
б) Спроецировать на эту плоскость каждую из прямых (проекция одной прямой, которая перпендикулярна плоскости,
будет точка, второй прямой – прямая).
в) Найти расстояние между проекциями прямых. Для удобства расчетов сечение дополнительной плоскостью
рекомендуется вынести отдельно)
Найти расстояние между прямыми в следующих задачах:
C1
B1
A1
B1
A1
D1
B
C
A
C1
Ребро куба
равно а
C
A
D
D
М
B1
A1
D1
B
C
A
C1
A1
D1
B
D
B1
C1
D
D
к
B
A
C
Правильная призма,
ребро основания 4
боковые ребра равны 6
(AC1,A1K)-?
B
C
B
A
A
D
Правильная пирамида,
ребро основания – 6
Боковое ребро – 5
(AD,MC) - ?
N
K
C
Правильная призма,
все ребра равны а
(AK,DN) - ?
B
A
O
K
C
Правильная пирамида
Высота пирамиды равна
высоте основания h
(AK, DB) -?

19.

Вариант 1
1. Дан прямоугольный параллелепипед ABCDA1B1C1D1, AB=8, AD=6, AA1=10, M –
середина ВВ1. Найти расстояние между прямыми: а) MD и AA1 ; б) AB и MD.
2. Дана правильная треугольная призма ABCA1B1C1, АВ=а, АА1=b. Найти расстояние
между прямыми ВА1 и В1С1.
3. Дана правильная треугольная пирамида ABCD, все ребра которой равны а, М, N–
середины ребер АС и ВС. Найти расстояние между прямыми AD и MN.
4. Из вершины В тупого угла ромба ABCD восстановлен перпендикуляр ВК к плоскости
ромба. Найти расстояние между прямыми АК и ВС, если угол А равен 30о, сторона
ромба равна а, ВК=b.
Вариант 2
1.
2.
3.
4.
Дан прямоугольный параллелепипед ABCDA1B1C1D1, AB=4, AD=3, AA1=12, M –
середина DD1. Найти расстояние между прямыми: а) BM и AA1 ; б) BM и DC.
Дана правильная треугольная призма ABCA1B1C1, АВ=а, АА1=b. Найти расстояние
между прямыми CK и В1С1 , где К – середина АА1.
Дана правильная четырехугольная пирамида ABCDS, все ребра которой равны а, М, N–
середины ребер BС и CD. Найти расстояние между прямыми AS и MN.
Из вершины В тупого угла ромба ABCD восстановлен перпендикуляр ВК к плоскости
ромба. Найти расстояние между прямыми АB и KD, если угол А равен 30о, сторона
ромба равна а, ВК=b.