Лицейский уровень. Стадия вызова

1.

8 класс . Лицейский уровень
Государственное общеобразовательное
учреждение лицей №265.
Вербицкий Сергей Николаевич

2.

- Содействовать формированию интеллектуальной, исследовательской ,
культуры учащихся (умению анализировать ,конкретизировать ,творчески
мыслить ,обобщать полученные знания ,размышлять и рассуждать ) .
- Развивать коммуникативные способности учащихся.
- Повторить свойства функций их графики
- Выработать алгоритм решения неравенства методом интервалов

3.

I.Стадия вызова
II. Стадия осмысления
III. Рефлексия

4.

1. Повторение свойств функций : y=f(x).
2. Слайд –шоу “Путешествие линии y=f(x)
в прямоугольной системе координат “

5.

У
Х
Какие значения может принимать функция?
Ответ: f(x)>0

6.

У
X1
Х
Какие значения принимает функция слева (справа)
от точки пересечения графика с осью ОХ?
Ответ: f(x)>0 при х<x1, f(x)<0 при х>x1

7.

У
X1
X2
Х
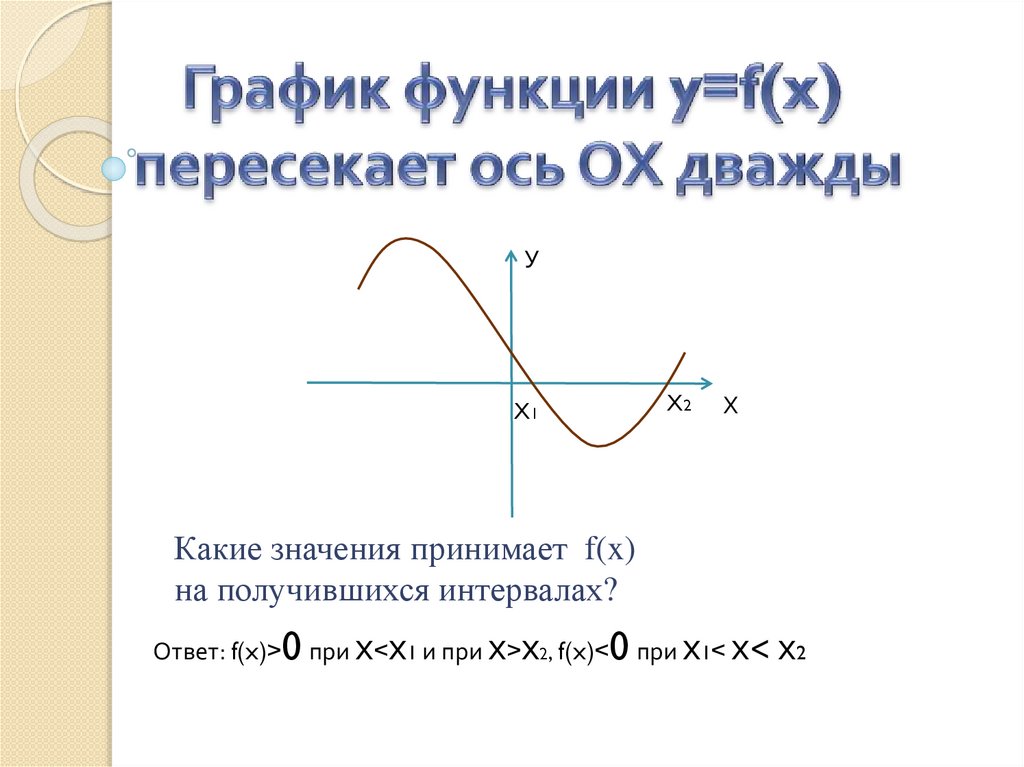
Какие значения принимает f(x)
на получившихся интервалах?
Ответ: f(x)>0 при х<x1 и при х>x2, f(x)<0 при x1< x<
x2

8.

У
Х1
Х2
Х3
Назвать интервалы знакопостоянства функции
Ответ: f(x)>0 при х<Х1 ; Х2< x< Х3 ; x> Х3
f(x)<0 при Х1 < x< Х3
Х

9.

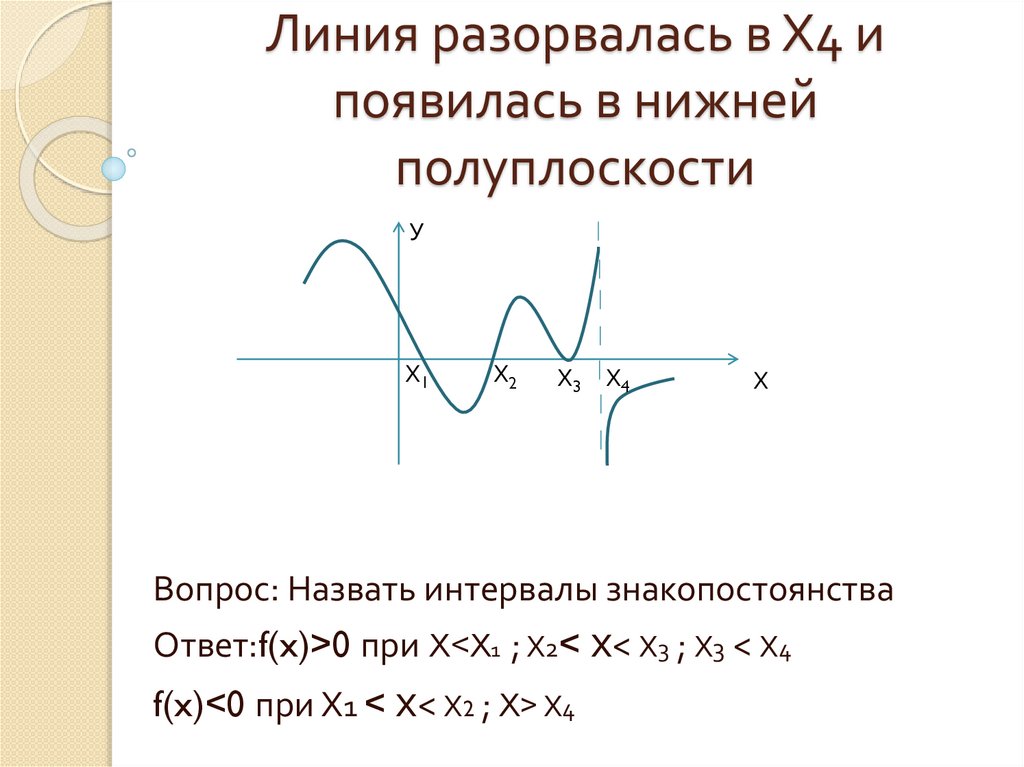
Линия разорвалась в Х4 и
появилась в нижней
полуплоскости
У
Х1
Х2
Х3 Х4
Х
Вопрос: Назвать интервалы знакопостоянства
Ответ:f(x)>0 при X<Х1 ; Х2< x< Х3 ; Х3 < Х4
f(x)<0 при Х1 < x< Х2 ; X> Х4

10.

11.

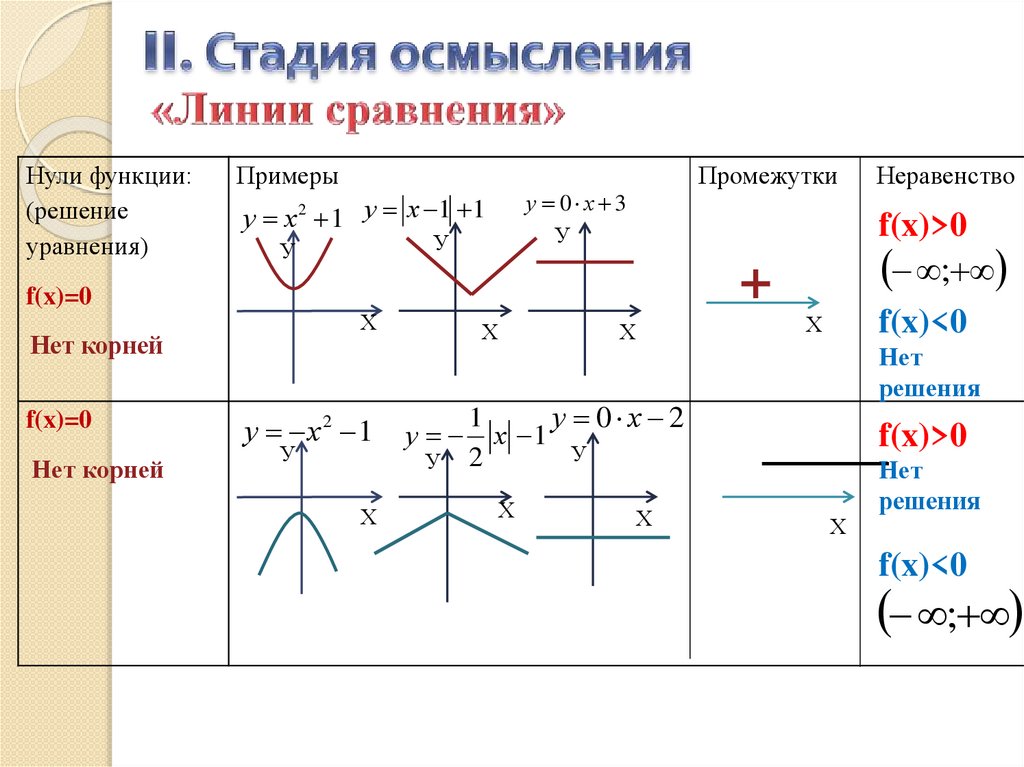
Нули функции:
(решение
уравнения)
Примеры
f(x)=0
Нет корней
У
у х2 1
У
Х
Х
Х
1
у 0 х 2
х 1
У
У 2
у
Х
Х
Неравенство
f(x)>0
f(x)>0
;
+
Х
Нет корней
f(x)=0
у 0 х 3
У
у х 2 1 у х 1 1
У
Промежутки
f(x)<0
Х
Нет
решения
f(x)>0
f(x)<0
Х
Нет
решения
f(x)<0
;

12.

2)
У
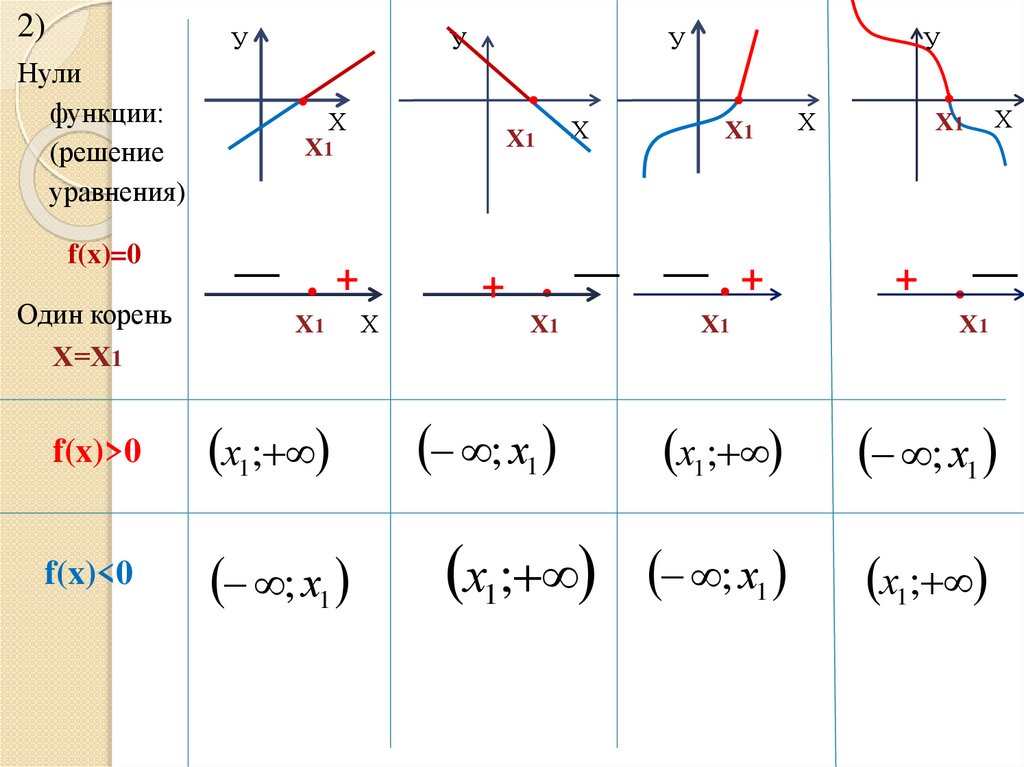
Нули
функции:
(решение
уравнения)
f(x)=0
Один корень
Х=Х1
У
У
Х
Х1
Х1
+
Х1
f(x)>0
х1;
f(x)<0
; х1
Х
Х1
; х1
Х
Х1
+
Х
У
+
Х
Х1
+
Х1
Х1
х1;
; х1
х1; ; х
х1;
1

13.

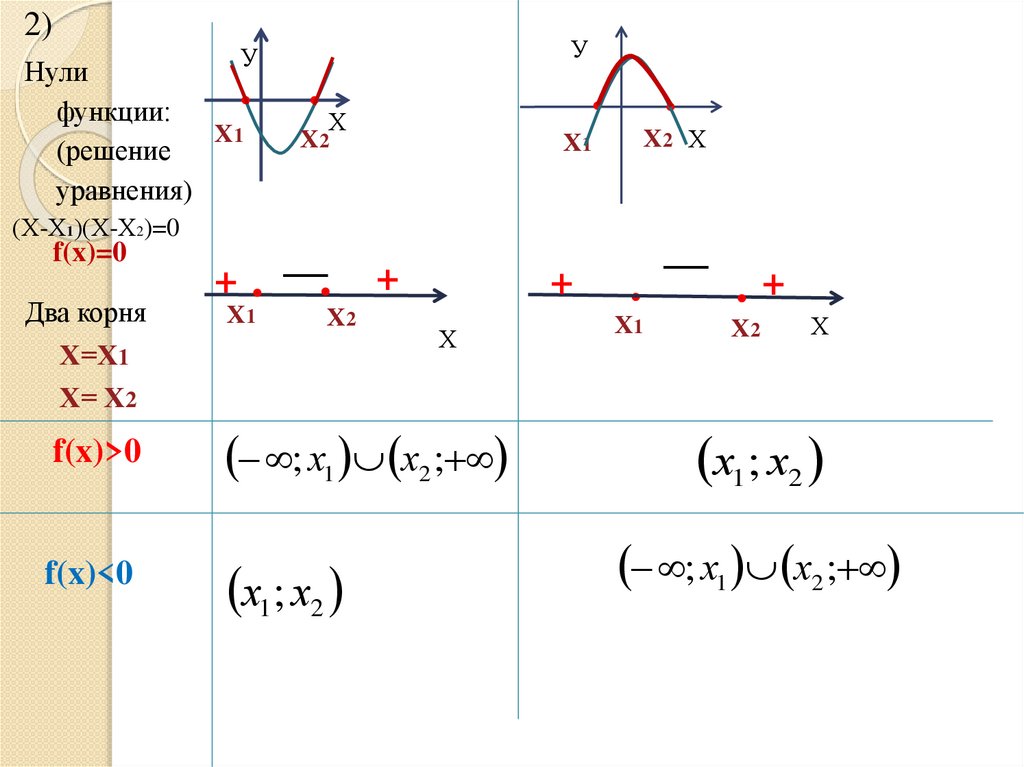
2)
У
У
Нули
функции:
Х1
(решение
уравнения)
(Х-Х1)(Х-Х2)=0
f(x)=0
Два корня
Х=Х1
Х= Х2
f(x)>0
f(x)<0
+
Х1
Х
Х2
Х2
+
+
Х
; х1 х2 ;
х1; х2
Х2 Х
Х1
Х1
+
Х2
Х
х1; х2
; х1 х2 ;

14.

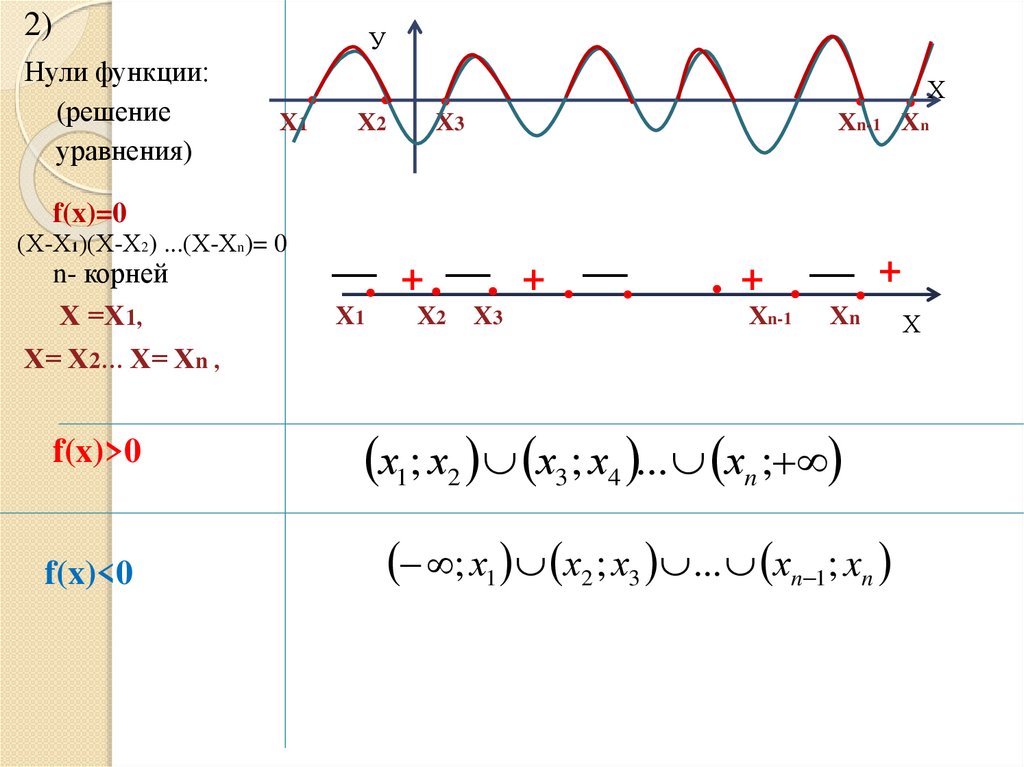
2)
У
Нули функции:
(решение
уравнения)
Х
Х1
Х2
Х3
Хn-1 Хn
f(x)=0
(Х-Х1)(Х-Х2) ...(Х-Хn)= 0
n- корней
Х =Х1,
Х= Х2… Х= Хn ,
f(x)>0
f(x)<0
Х1
+
Х2
Х3
+
+
Хn-1
+
Хn
х1; х2 х3 ; х4 ... хn ;
; х1 х2 ; х3 ... хn 1; xn
Х

15.

2. Сформулировать алгоритм решения
неравенств методом интервалов, если
f(x) - многочлен
А) Решить уравнение f(x)=0
Б) Найденные корни разместить на ось Х
В) Определить знаки интервалов
Г) Выбрать необходимые интервалы и записать
ответ

16.

3. Образец решения неравенств методом
интервалов: х 2 4 0
А)
х2 4 0
х 2
Б)
-2
х 2
В)
f(3) = 9-4=5>0 f(0) = 0-4= -4<0
Г)
Ответ:
x 2 или
+.
_ 2. + х
f(-3) = 9-4=5>0
x 2
; 2 2;

17.

III. Рефлексия
Обучающая самостоятельная
работа
2. Синквейн на тему «Метод
интервалов»
1.

18.

Обучающая самостоятельная
работа
II Вариант
I Вариант
1.
х 1 0
2
2. x 1 0
3. x 1 x 1 0
1
0
4.
x
5.
x 1 x 1 0
2
1
1. х 0
2
2
2. x 1 0
3. x 1 x 1 0
4.
1
0
x
5.
x 1 x 1 2 0

19.

Синквейн на тему
«Метод интервалов»
1. Знаки интервалов
2. Знакопостоянство интервалов
3. Упрощает решение
4. Применяется при движении снарядов, сбрасывании
грузов с самолетов и вертолетов и т.д.
5. Решение неравенств