Similar presentations:
Способы устных решений квадратных уравнений
1.
Способы устныхрешений квадратных
уравнений
МБОУ «СОШ №8», г. Канаш ЧР
Автор: учитель математики Халиулина Л.И.
2.
ОпределениеКвадратным уравнением называется уравнение
вида ax2 + bx + c = 0, a=/0.
Квадратные уравнения бывают:
полными ax2 + bx + c = 0
неполными ax2 + c = 0 или ax2 + bx = 0
приведенными x2 + px + q = 0.
3.
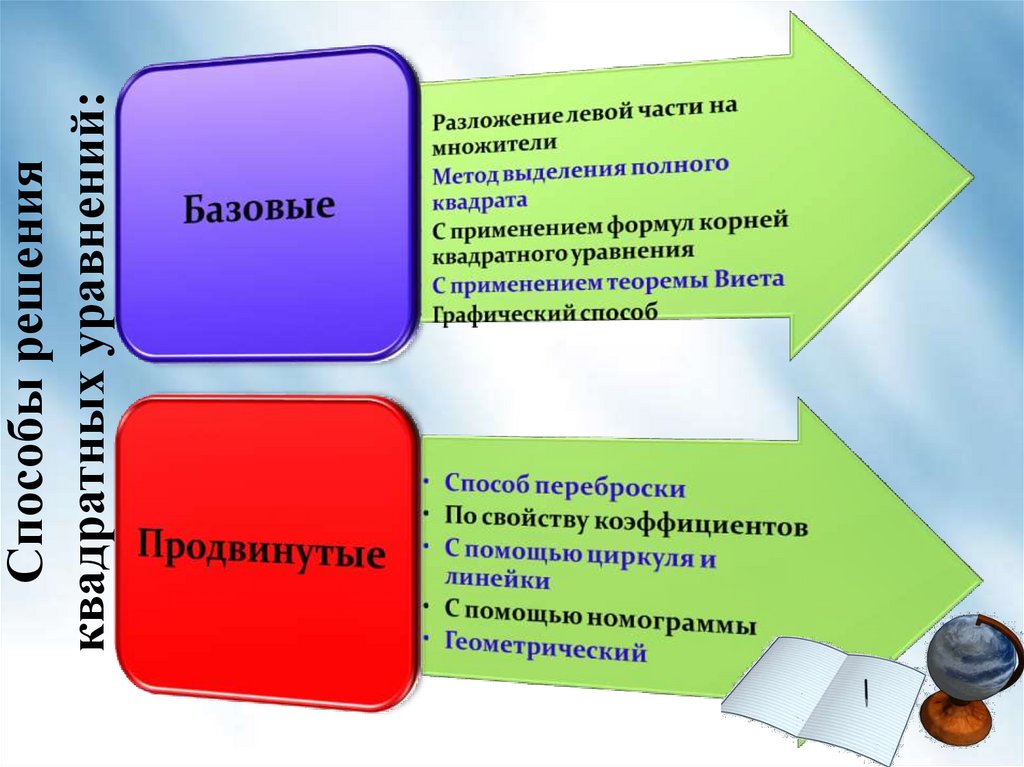
Способы решенияквадратных уравнений:
4.
1. Свойства коэффициентов квадратного уравнения.Пусть дано квадратное уравнение
ах2 + bх + с = 0, где а ≠0.
Свойство 1.
Если а + b + с = 0 (т е. сумма коэффициентов
уравнения равна нулю), то х1 = 1, х2 = с/а
Свойство 2.
Если а – b + с = 0, или b = а + с, то
х1 = – 1, х2 = – с/а
5.
2. Способ переброски.Пусть дано квадратное уравнение
ах2 + bх + с = 0, где а ≠0.
Если а±b+c≠0, то используется прием переброски
При этом способе коэффициент а умножается на свободный член, как
бы «перебрасывается» к нему, поэтому его и называют способом
«переброски». Этот способ применяют, когда можно легко найти
корни уравнения, используя теорему Виета и, что самое важное, когда
дискриминант есть точный квадрат.
Пример.
2х2 – 11х+5=0, 2-11+5=-4, 2*5=10
х2 – 11х+10= 0
х = 10; х =1.
Корни уравнения необходимо поделить на а=2.
Ответ: 5; 0,5.
6.
3. Закономерность коэффициентов (а=с)1) Если в уравнении ax2 + bx + c = 0 коэффициент b равен (а2 +1), а
коэффициент с численно равен коэффициенту а (ax2 + (а2 +1)∙ х+
а= 0), то его корни равны
Пример. Рассмотрим уравнение 6х2 +37х +6 = 0.
х = –6; х = – .
2) Если в уравнении ax2 – bx + c = 0 коэффициент b равен (а2 + 1),а
коэффициент с численно равен коэффициенту а (ax2 - (а2 +1)∙ х+
а= 0), то его корни равны
Пример. Рассмотрим уравнение 15х2 –226х +15 = 0.
х = 15; х = – .
7.
3) Если в уравнении ax2 + bx – c = 0 коэффициент b равен (а2 – 1), акоэффициент с численно равен коэффициенту а
(ax2 + (а2– 1)∙ х– а= 0), то его корни равны
Пример. Рассмотрим уравнение 17х2 +288х – 17 = 0.
х = –17; х = .
4) Если в уравнении ax2 – bx – c = 0 коэффициент b равен (а2 – 1), а
коэффициент с численно равен коэффициенту а
(ax2 + (а2– 1)∙ х– а= 0), то его корни равны
Пример. Рассмотрим уравнение 10х2–99 х – 10 = 0.
х = 10; х = –
.
8.
Вывод:«Человеку, изучающему алгебру, часто
полезнее решить одну и ту же задачу тремя
различными способами, чем решить тричетыре различные задачи. Решая одну
задачу различными методами, можно путем
сравнений выяснить, какой из них короче и
эффективнее. Так вырабатывается опыт»
У. Сойер
9.
Литература1. http://arm-math.rkc74.ru/DswMedia/resheniekvadratnyixuravneni
yrazlichnyimisposobami.doc
2. http://edu.of.ru/attach/17/76716.doc








 mathematics
mathematics








