Similar presentations:
Методика решения задач по теории вероятностей при подготовке к сдаче ГИА и ЕГЭ
1. Методика решения задач по теории вероятностей при подготовке к сдаче ГИА и ЕГЭ
2.
Высшееназначение математики…
состоит в том, чтобы находить скрытый порядок в хаосе,
который нас окружает.
Н.Винер
3.
4.
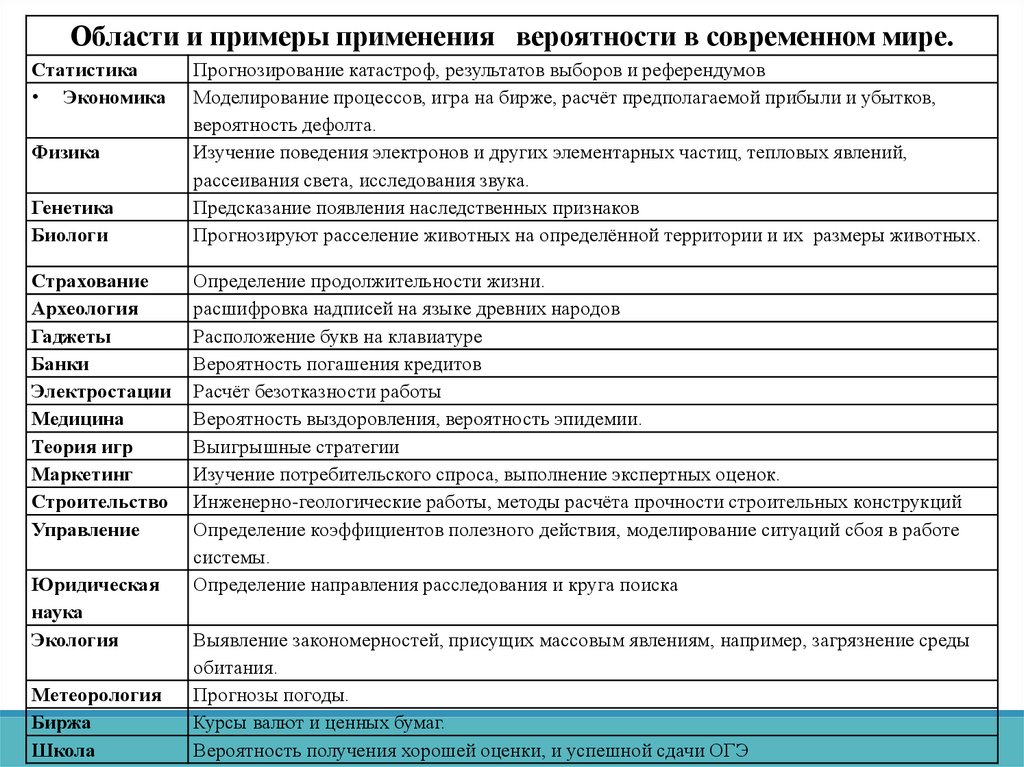
Области и примеры применения вероятности в современном мире.Статистика
• Экономика
Физика
Генетика
Биологи
Страхование
Археология
Гаджеты
Банки
Электростации
Медицина
Теория игр
Маркетинг
Строительство
Управление
Юридическая
наука
Экология
Метеорология
Биржа
Школа
Прогнозирование катастроф, результатов выборов и референдумов
Моделирование процессов, игра на бирже, расчёт предполагаемой прибыли и убытков,
вероятность дефолта.
Изучение поведения электронов и других элементарных частиц, тепловых явлений,
рассеивания света, исследования звука.
Предсказание появления наследственных признаков
Прогнозируют расселение животных на определённой территории и их размеры животных.
Определение продолжительности жизни.
расшифровка надписей на языке древних народов
Расположение букв на клавиатуре
Вероятность погашения кредитов
Расчёт безотказности работы
Вероятность выздоровления, вероятность эпидемии.
Выигрышные стратегии
Изучение потребительского спроса, выполнение экспертных оценок.
Инженерно-геологические работы, методы расчёта прочности строительных конструкций
Определение коэффициентов полезного действия, моделирование ситуаций сбоя в работе
системы.
Определение направления расследования и круга поиска
Выявление закономерностей, присущих массовым явлениям, например, загрязнение среды
обитания.
Прогнозы погоды.
Курсы валют и ценных бумаг.
Вероятность получения хорошей оценки, и успешной сдачи ОГЭ
5.
Игры в костиКарточные игры
Лотерея
Игровые автоматы
6.
7. Классическое определение вероятности
Вероятностью события А называют отношениечисла благоприятствующих этому событию исходов
к общему числу всех равновозможных
несовместных элементарных исходов, образующих
полную группу.
m
P ( A)
n
8.
Задачи ОГЭ на прямое использованиеклассического определения вероятности
ЗАДАЧИ В ОДНО ДЕЙСТВИЕ
ТАХИ
ПАЗЛЫ
ПИРОЖКИ
ЗАДАЧИ В ДВА ДЕЙСТВИЯ
БАБУШКИНЫ ЧАШКИ
СПОРТСМЕНЫ
БИЛЕТЫ НА ЭКЗАМЕНЕ
ФОНАРИКИ
В задачах про спортсмены надо обратить внимание на формулировку вопроса. В
одних вариантах нужно найти вероятность того, что первым будет стартовать
спортсмен из России, а в других - НЕ из России.
9.
1.На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугадвыбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение:
m=4 – число пирожков с вишней (число благоприятных исходов)
n=16 – число всех пирожков (общее число равновозможных исходов)
2. Родительский комитет закупил 20 пазлов для подарков детям в связи с
окончанием учебного года, из них 10 с машинами и 10 с видами городов.
Подарки распределяются случайным образом между 20 детьми, среди которых
есть Коля. Найдите вероятность того, что Коле достанется пазл с машиной.
Решение:
m=10 – число пазлов с машинами(число благоприятных исходов)
n=20 – число всех пазлов(общее число равновозможных исходов)
10.
3. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США,остальные — из Китая. Порядок, в котором выступают гимнастки, определяется
жребием. Найдите вероятность того, что спортсменка, выступающая первой,
окажется из Китая.
Решение:
m=20-8-7=5 – число гимнасток из Китая (число благоприятных исходов)
n=20 – число гимнасток, которые принимают участие в чемпионате (общее
число равновозможных исходов)
4.В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из
Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют,
определяется жребием. Найдите вероятность того, что первым будет стартовать
спортсмен не из России.
Решение:
m=6+3=9 число спортсменов не из России (число благоприятных исходов
n=20- число спортсменок , которые принимают участие в лыжных гонках
(общее число равновозможных исходов)
11.
5. У бабушки 10 чашек, 7 с красными цветами, остальные с синими.Бабушканаливает чай в случайно выбранную чашку. Найдите вероятностьтого, что это
будет чашка с синими цветами.
Решение:
12.
Задачи на нахождение вероятностипротивоположного события
Билеты на экзамене
Фанарики
Ручки
Надо обратите внимание, что дается количество невыученных билетов, а
спрашивается вероятность выученных, что указано количество неисправных
фонариков, а вероятность нужно найти для исправных.
13.
7. На экзамене 60 билетов, Олег не выучил 12 из них. Найдите вероятность того,что ему попадётся выученный билет.
Решение:
1 способ:
Задачи про фонарики решаем аналогичными
способами.
14.
ОСНОВНЫЕ ТЕОРЕМЫ О ВЕРОЯТНОСТЕЙСОБЫТИЙ
.
• Противоположные
события - если не произошло событие A, то точно
произошло событие B: P(B)=1−P(A);
Независимые события - вероятность одного события никак не зависит от
наступления другого события. Вероятность, что независимые события A и B
произошли одновременно: P(A и B)=P(A)∗P(B);
Несовместные события - события, которые не могут произойти одновременно.
Вероятность, что произошло одно из несовместных событий A или B:
P(A или B)=P(A)+P(B);
Совместные события - события A и B, которые могут произойти одновременно.
Вероятность, что произойдет или событие A, или B,
или они оба:
P(A или B)=P(A)+P(B)−P(A и B)
15.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19.Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что
эта ручка пишет хорошо.
1-0,19=0,81













 mathematics
mathematics








