Similar presentations:
Аксиомы стереометрии
1.
Аксиомыстереометрии.
2.
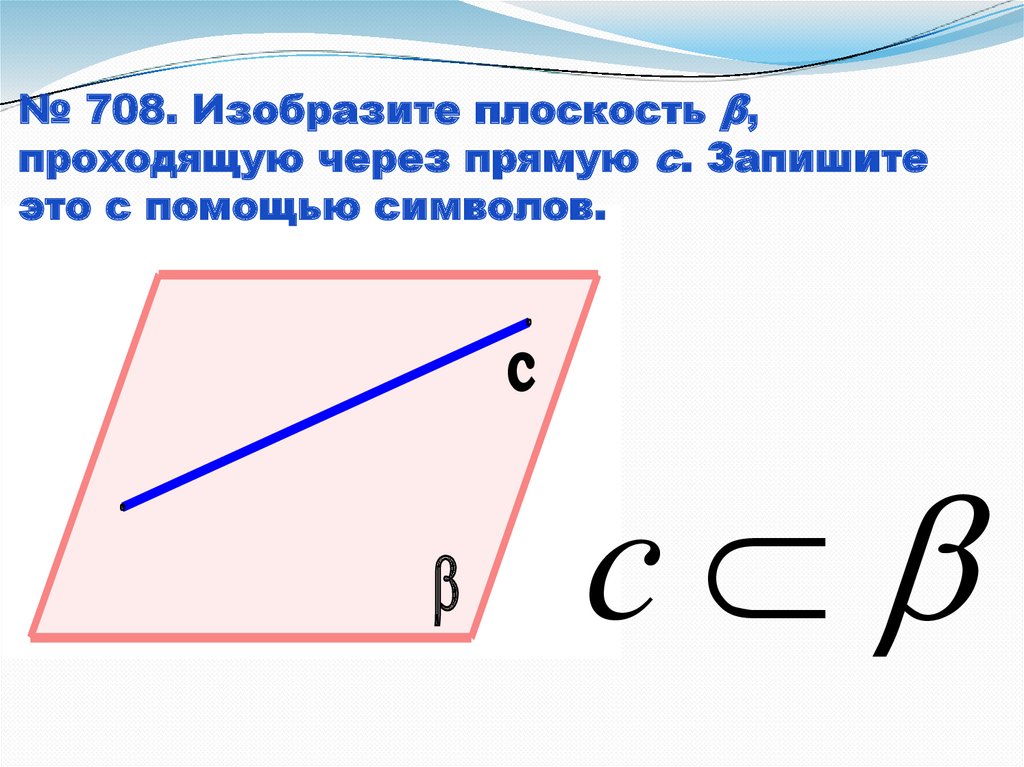
№ 708. Изобразите плоскость β,проходящую через прямую с. Запишите
это с помощью символов.
c
с
3.
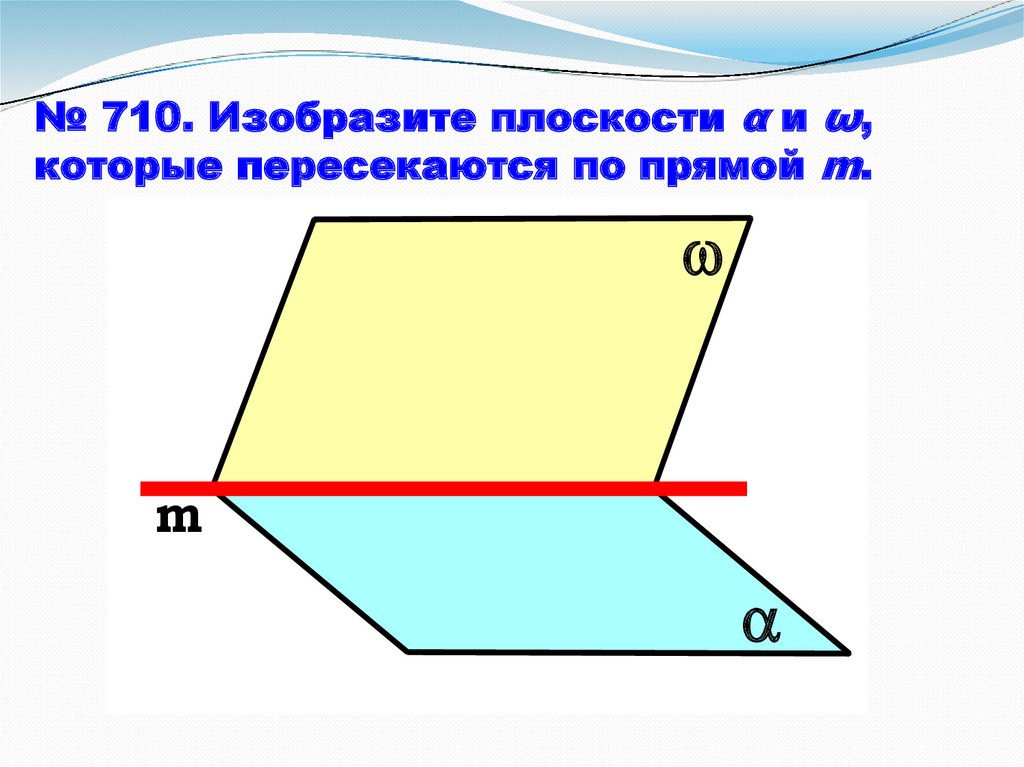
№ 710. Изобразите плоскости α и ω,которые пересекаются по прямой m.
m
4.
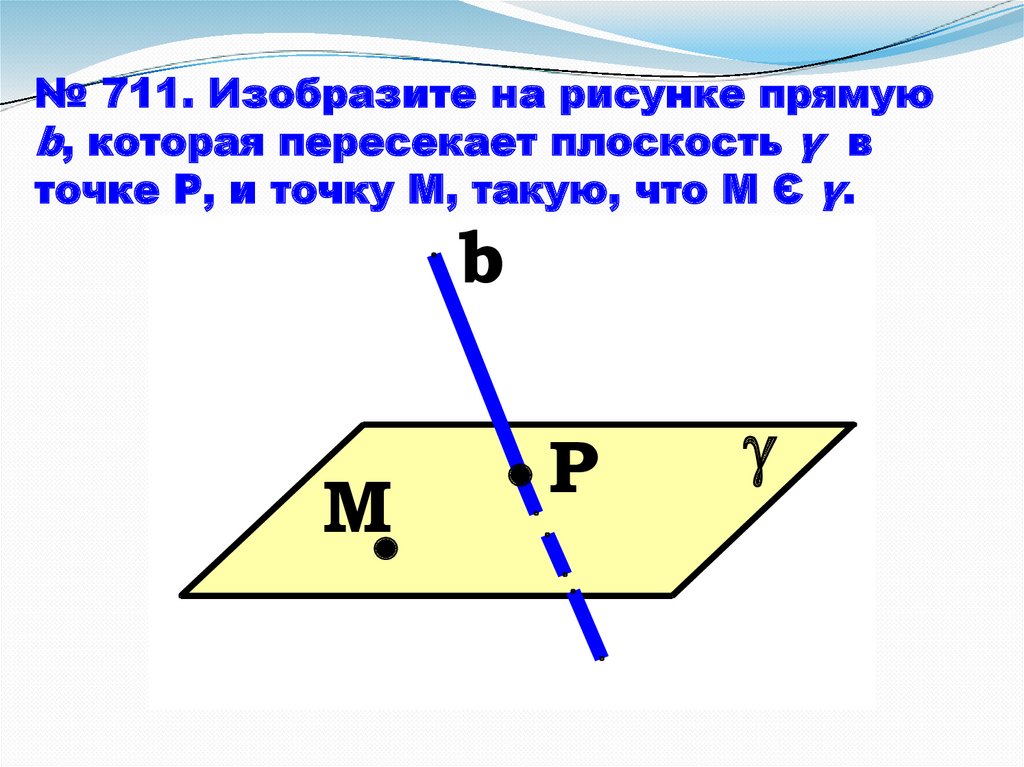
№ 711. Изобразите на рисунке прямуюb, которая пересекает плоскость γ в
точке Р, и точку М, такую, что М Є γ.
b
M
P
5.
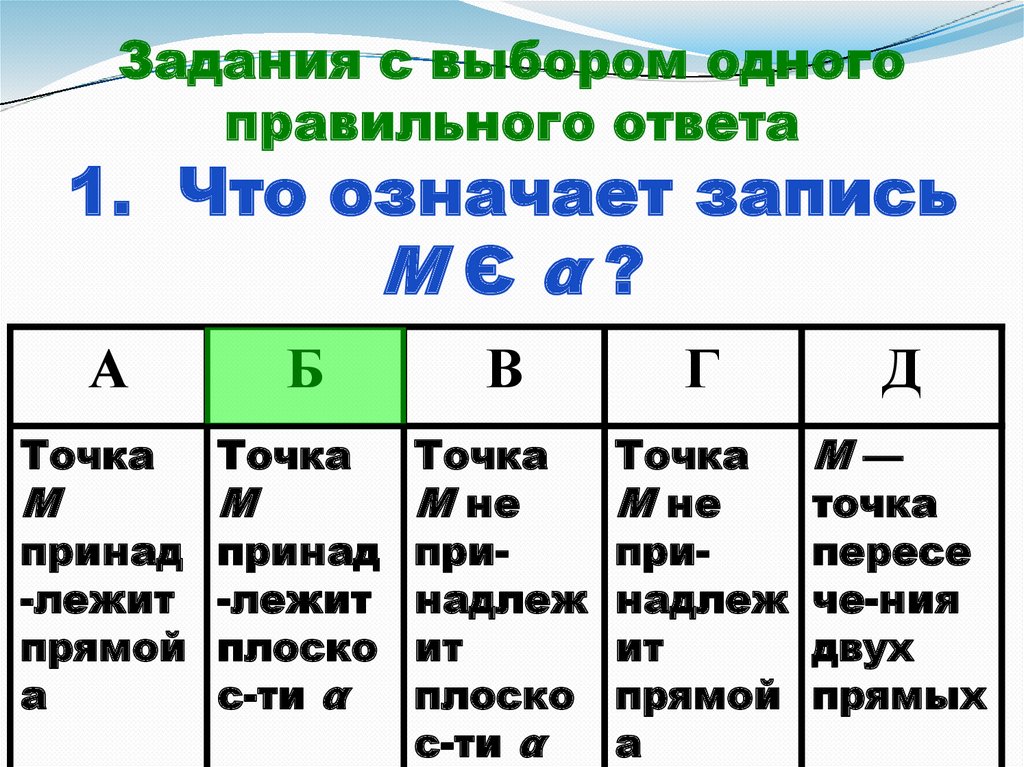
Задания с выбором одногоправильного ответа
1. Что означает запись
МЄα?
А
Точка
Б
Точка
В
Точка
М
М
М не
принад принад при-лежит -лежит надлеж
прямой плоско ит
а
с-ти α
плоско
с-ти α
Г
Точка
М не
принадлеж
ит
прямой
а
Д
М—
точка
пересе
че-ния
двух
прямых
6.
Задания с выбором одногоправильного ответа
2. Что означает запись
b γ ?
А
Б
В
Г
Д
Прямая b
принадлежит
плоскости γ
Точка b
принадлежит
плоскости γ
Точка b
не принадлежит
плоскости γ
Прямая b
не принадлежит
плоскости γ
Прямая b
-прямая
пересечения двух
плоскостей
7.
Задания с выбором одногоправильного ответа
3. Среди данных утверждений выберите
верное.
Основными фигурами (понятиями) в
стереометрии являются.
1. Точка
4. Луч
2. Треугольник
5. Прямая
3. Плоскость
6. Призма
А
Б
В
Г
Д
Только Только Только Только Только
3
3, 6
1, 5 1, 3, 5, 6 1, 3, 5
8.
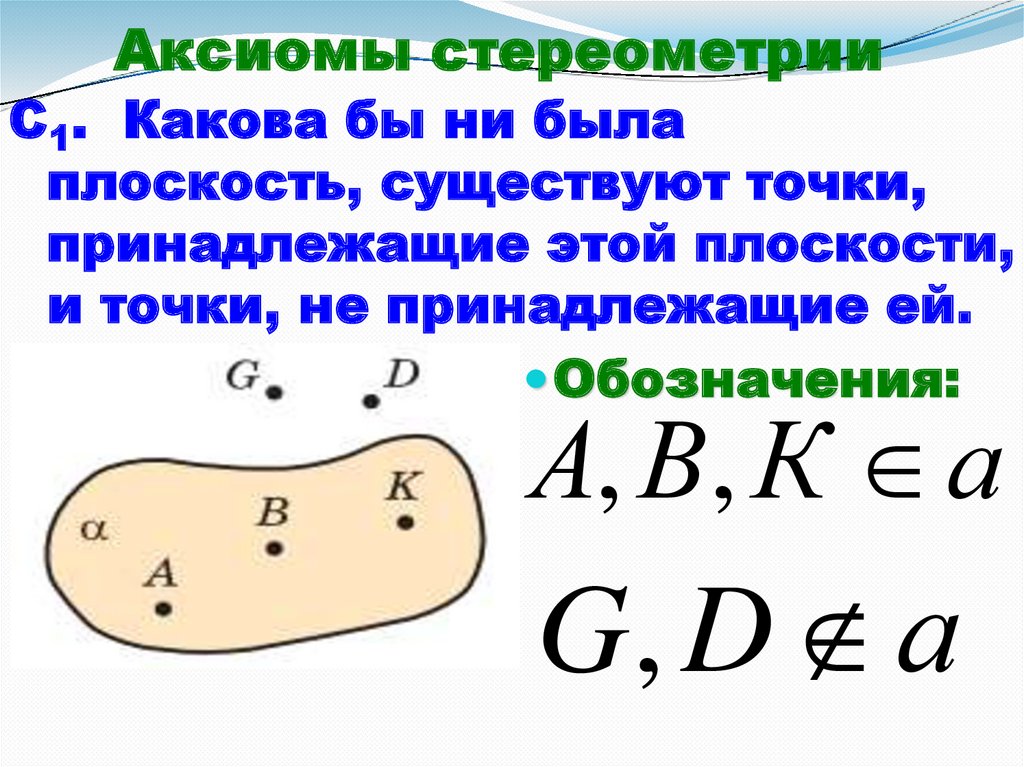
Аксиомы стереометрииС1. Какова бы ни была
плоскость, существуют точки,
принадлежащие этой плоскости,
и точки, не принадлежащие ей.
Обозначения:
А, В, К а
G, D а
9.
Аксиомы стереометрииС2. Если две различные
плоскости имеют общую точку,
то они пересекаются по прямой,
проходящей через эту точку .
Обозначения:
;
а , а ;
то а
10.
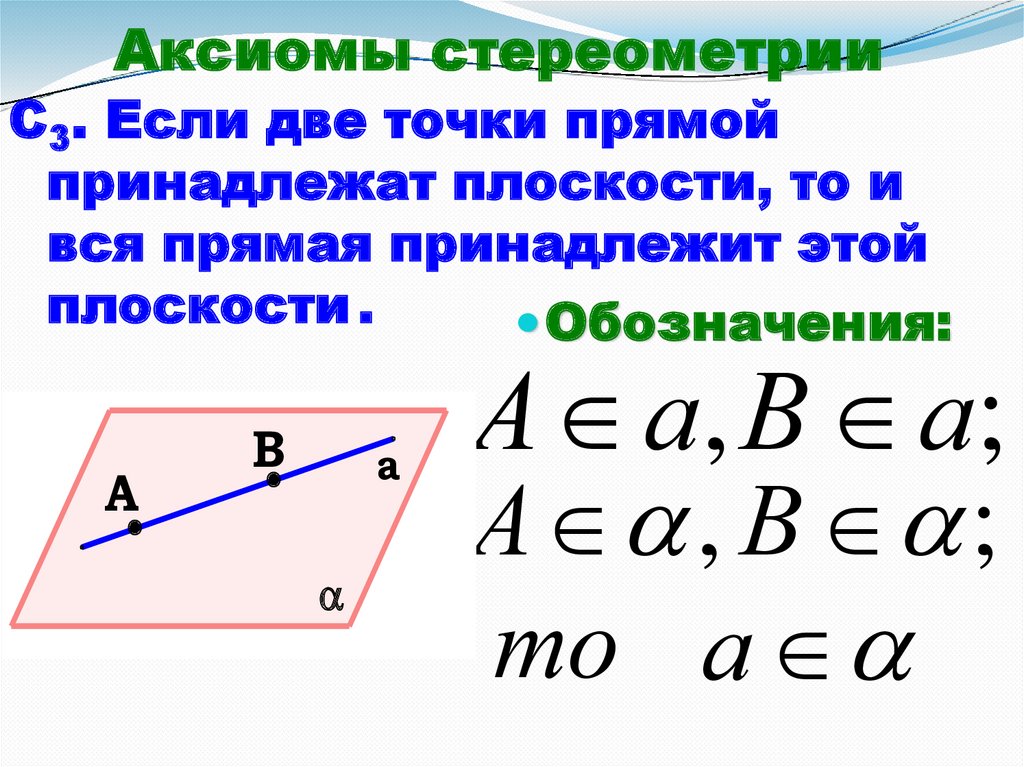
Аксиомы стереометрииС3. Если две точки прямой
принадлежат плоскости, то и
вся прямая принадлежит этой
плоскости .
Обозначения:
А
В
а
А а, В а;
А , В ;
то а
11.
Аксиомы стереометрииС4. Через три точки, не лежащие
на одной прямой, можно
провести плоскость, и притом
только одну .
Обозначения:
А
В
С
А, В, С а;
то А, В, С ,
α - единственная
12.
Решение задачУч.с.161 Бевз № 744(1,2). Начертите куб
АВСDА1В1С1D1. Запишите с помощью
символов ответы на следующие вопросы:
а) По каким прямым пересекаются
плоскости:
1) (АВС) и (АА1D1); 2) (АА1В1) и (АА1D1).
б) Каким плоскостям принадлежат точки:
1) А;
2) С1.
в) Принадлежит ли точка В1 плоскости:
1) (АВС);
2) (DD1С1).
13.
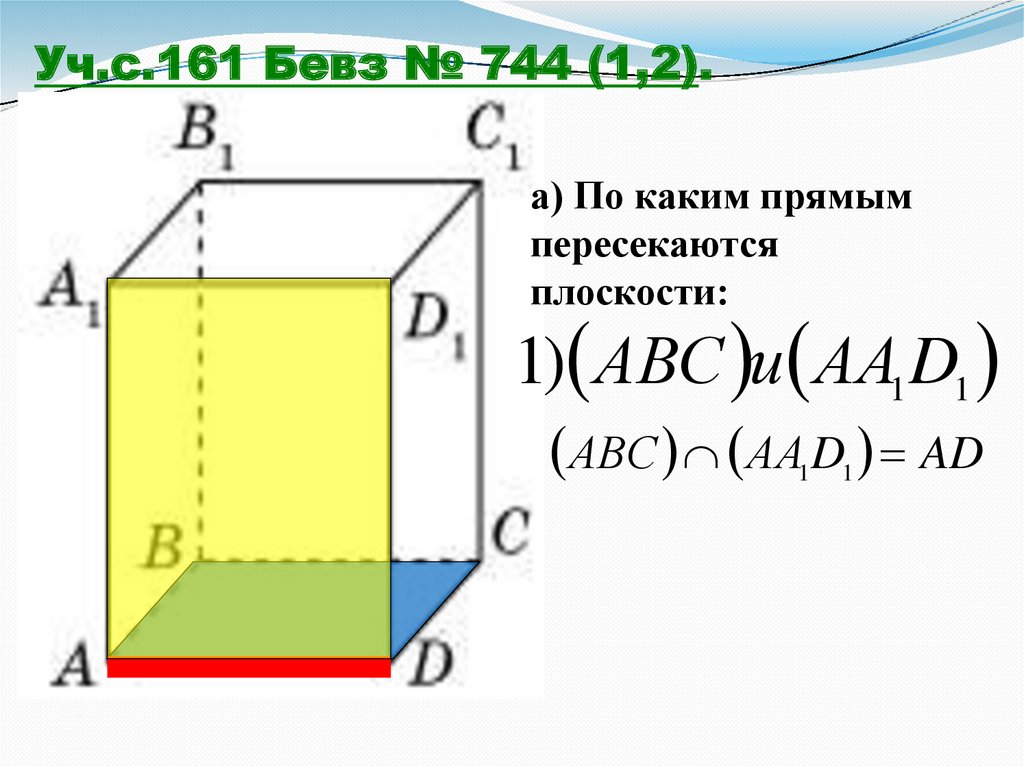
Уч.с.161 Бевз № 744 (1,2).а) По каким прямым
пересекаются
плоскости:
1) АВС и АА1 D1
1) АВС АА1 D1 AD;
АВС АА D AD
1
1
14.
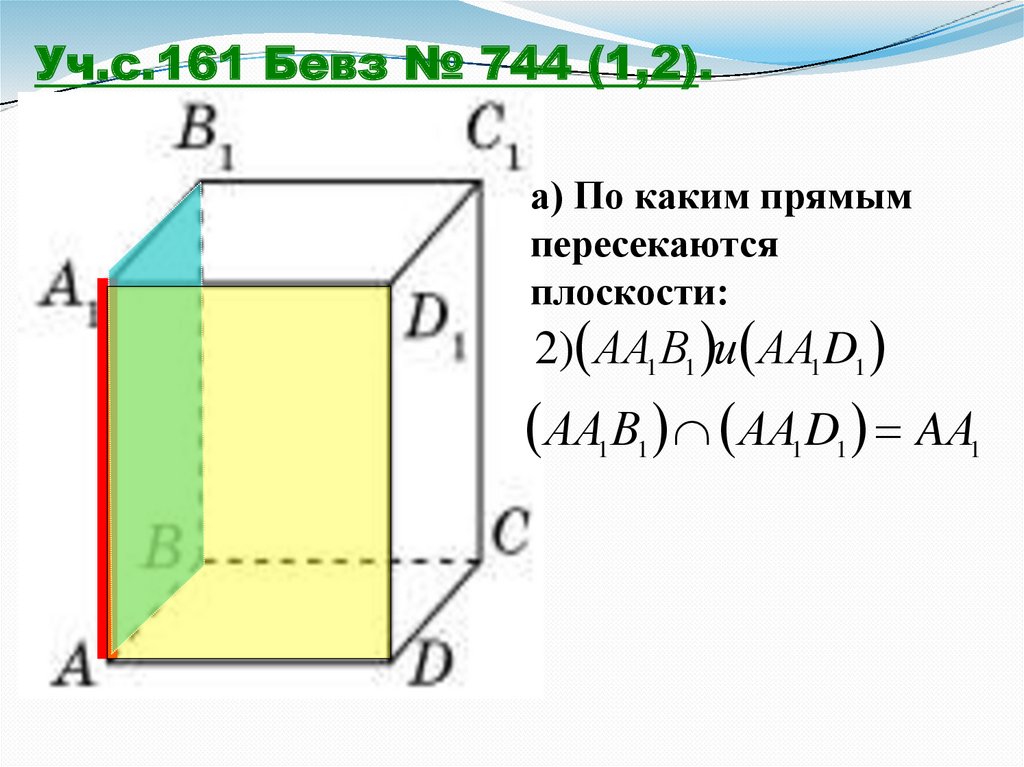
Уч.с.161 Бевз № 744 (1,2).а) По каким прямым
пересекаются
плоскости:
2) АА1 В1 и АА1 D1
1) АВС АА1 D1 AD;
АА В АА D AА
1
1
1
1
1
15.
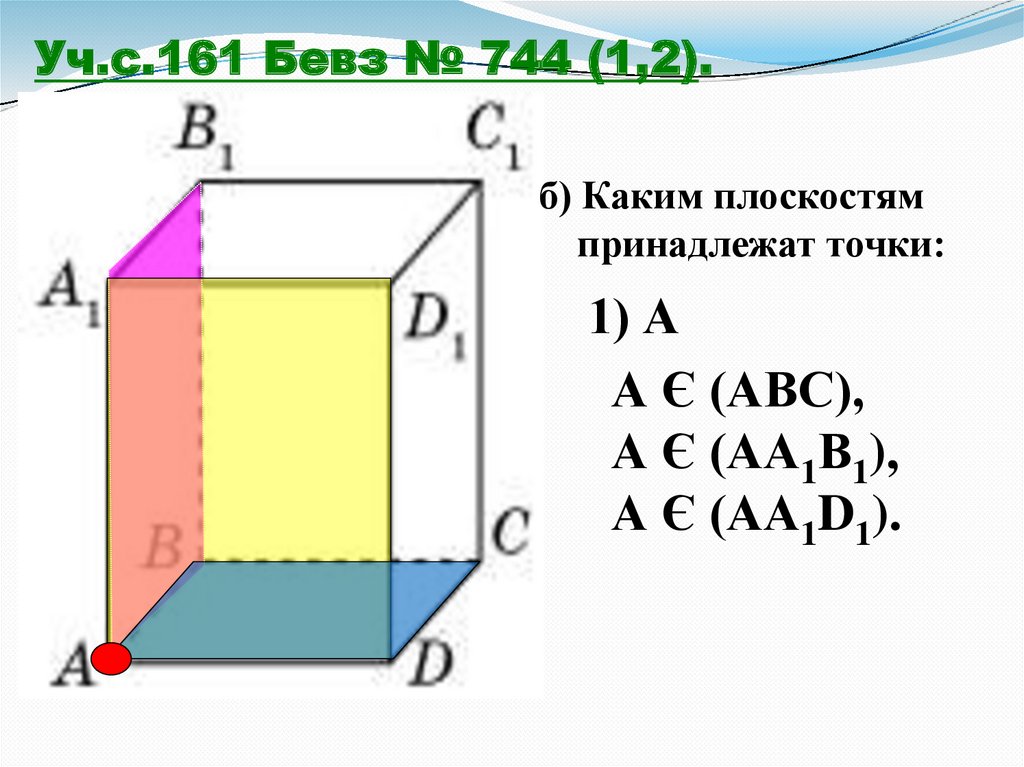
Уч.с.161 Бевз № 744 (1,2).б) Каким плоскостям
принадлежат точки:
1) АВС АА1 D1 AD;
1) АВС АА1 D1 AD;
1) А
А Є (АВС),
А Є (АА1В1),
А Є (АА1D1).
16.
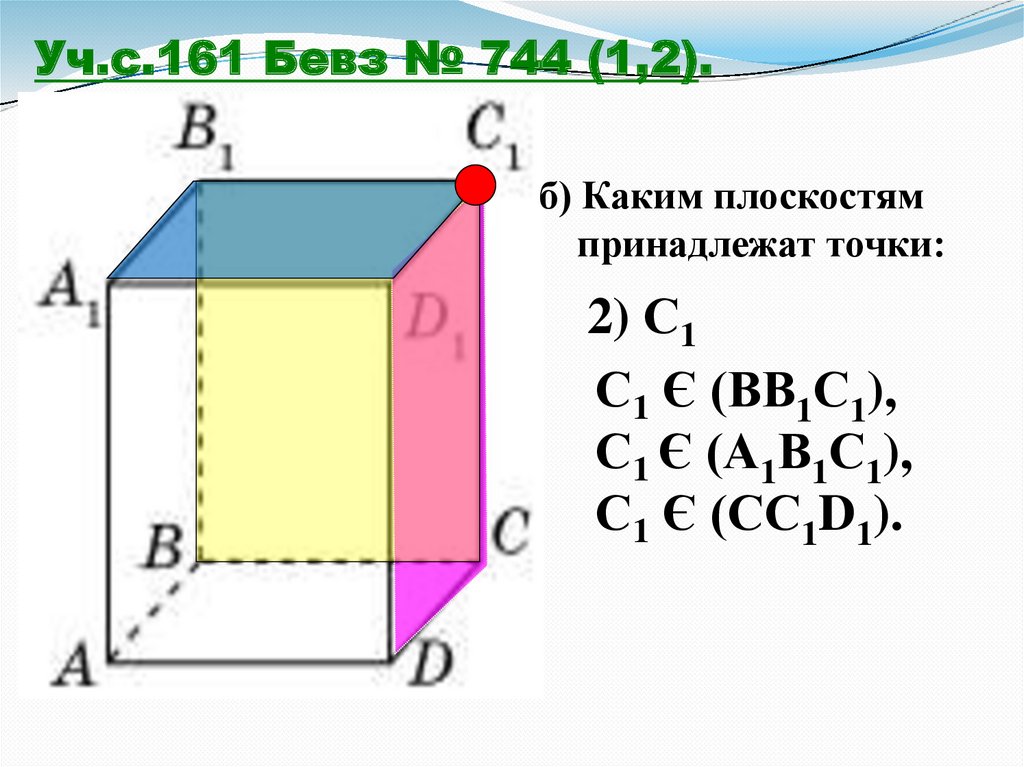
Уч.с.161 Бевз № 744 (1,2).б) Каким плоскостям
принадлежат точки:
1) АВС АА1 D1 AD;
1) АВС АА1 D1 AD;
2) С1
С1 Є (ВВ1С1),
С1 Є (А1В1С1),
С1 Є (СС1D1).
17.
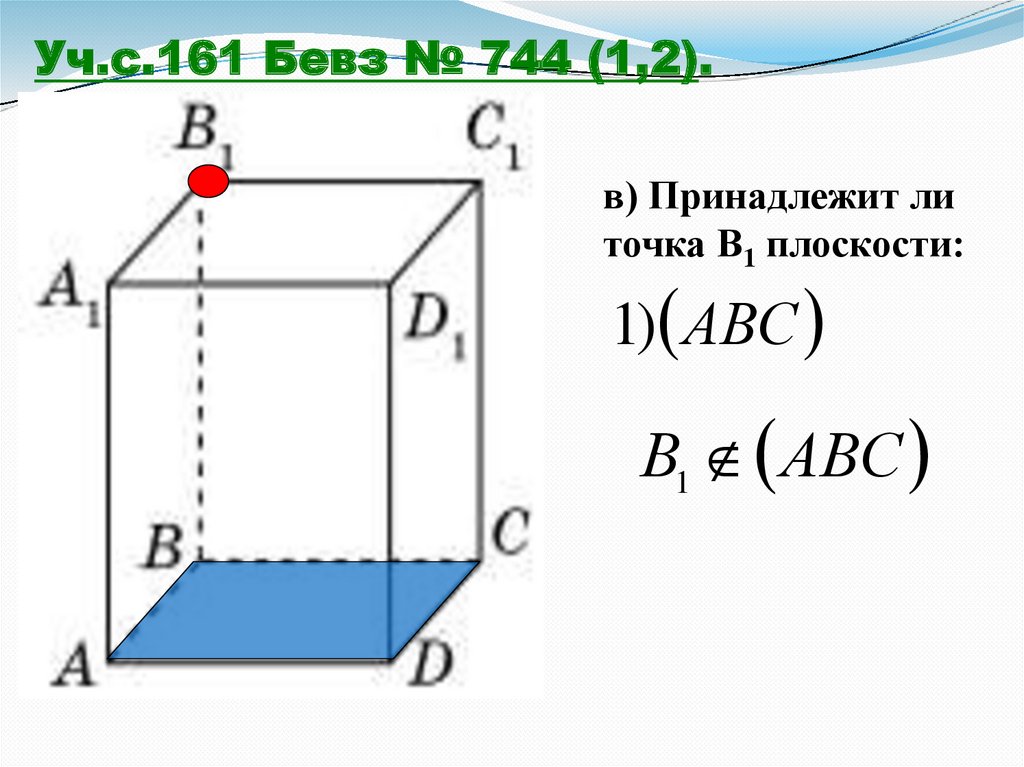
Уч.с.161 Бевз № 744 (1,2).в) Принадлежит ли
точка В1 плоскости:
1) АВС АА1 D1 AD;
1) АВС
В1 АВС
1) АВС АА1 D1 AD;
18.
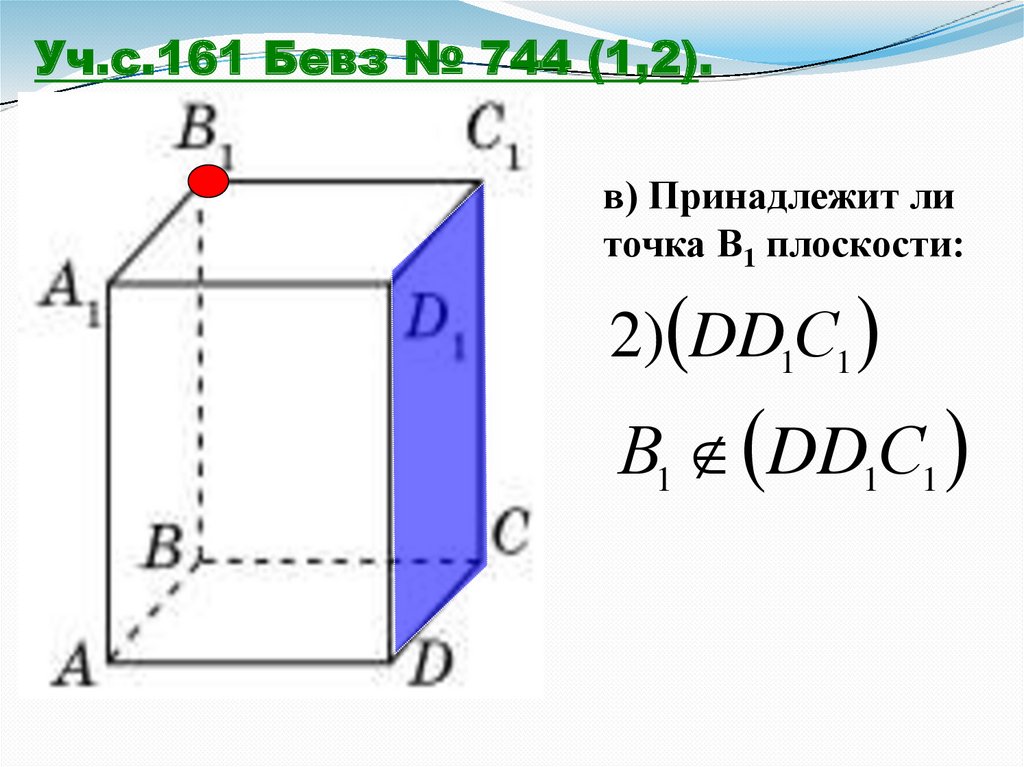
Уч.с.161 Бевз № 744 (1,2).в) Принадлежит ли
точка В1 плоскости:
1) АВС АА1 D1 AD;
2) DD1С1
В1 DD1С1
1) АВС АА1 D1 AD;
19.
Решение задачСб.с.13 № 83. Можно ли утверждать, что:
1) любые две точки всегда лежат на одной
прямой;
2) любые четыре точки всегда лежат в
одной плоскости?
Сб.с.13 № 84. Могут ли две различные
плоскости иметь только одну общую
точку?
20.
Домашнее задание.10-Т, М
Г.П. Бевз Математика 10
§ 20 (выучить теорию)
№ 744(3).
Сб.с. 44 № 83,84.







 mathematics
mathematics








