Арифметические схемы. Арифметико-логическое устройство

1.

Арифметические схемы
Арифметико-логическое устройство
Накапливающий
регистр
регистр
1. Устройство управления получает команду (из запоминающего устройства), которая
дает указание сложить число из конкретной ячейки памяти (адреса) с числом из
накапливающего регистра.
2. Число, которое надо прибавить, передается из памяти в регистр В. Число, хранящееся
теперь в регистре В, складывается с числом из накапливающего регистра с помощью
логических схем (по команде из устройства управления). Результат записывается в
накапливающий регистр.
3. Новое число, которое остается в аккумуляторе, может быть сложено со следующим
числом из памяти и т.д. Если же конкретный математический процесс завершен, это
число может быть передано в память для дальнейшего хранения.

2.

Арифметические схемы
Схема сложения

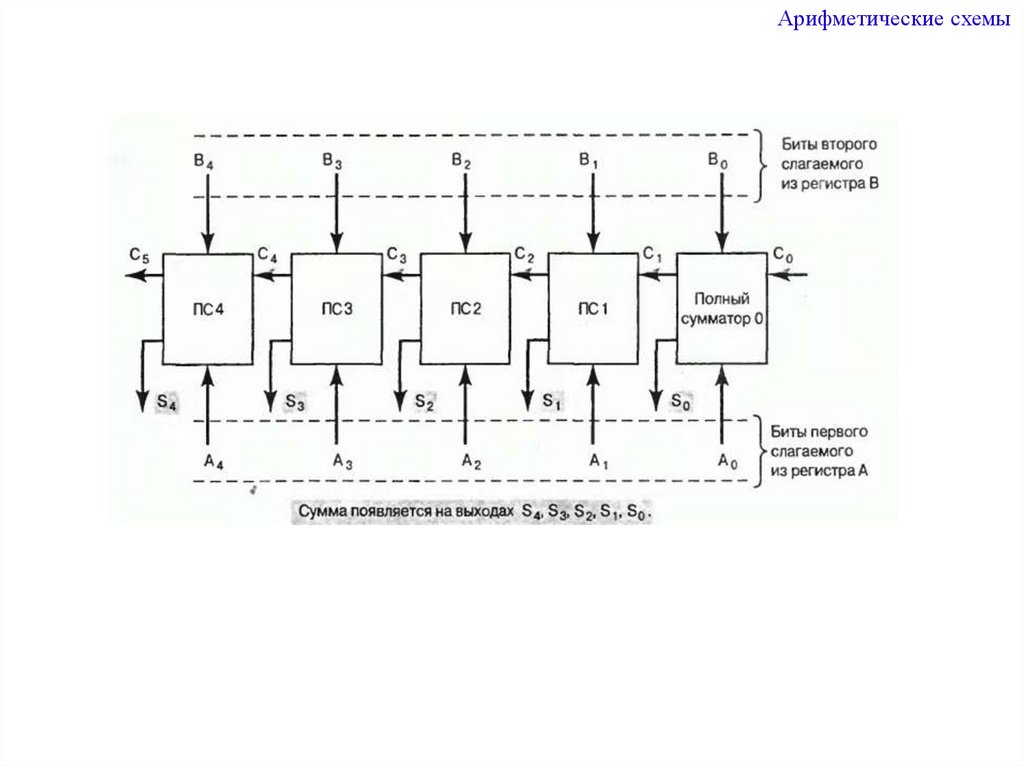
3.

Арифметические схемы

4.

Принцип работы полного сумматора
Арифметические схемы

5.

Арифметические схемы
Карно для выхода S. Эта карта вообще не имеет прилегающих друг к другу ячеек с
единицами, поэтому их невозможно сгруппировать, чтобы получить квартеты или
даже пары, т.е. выражение для выхода S не может быть минимизировано. Такой
результат демонстрирует ограничения метода карт Карно по сравнению с
алгебраическим методом. Используя последний, можно минимизировать выражение
на выходе S, вынося общие множители и применяя операцию исключающее ИЛИ и
исключающее ИЛИ-НЕ.

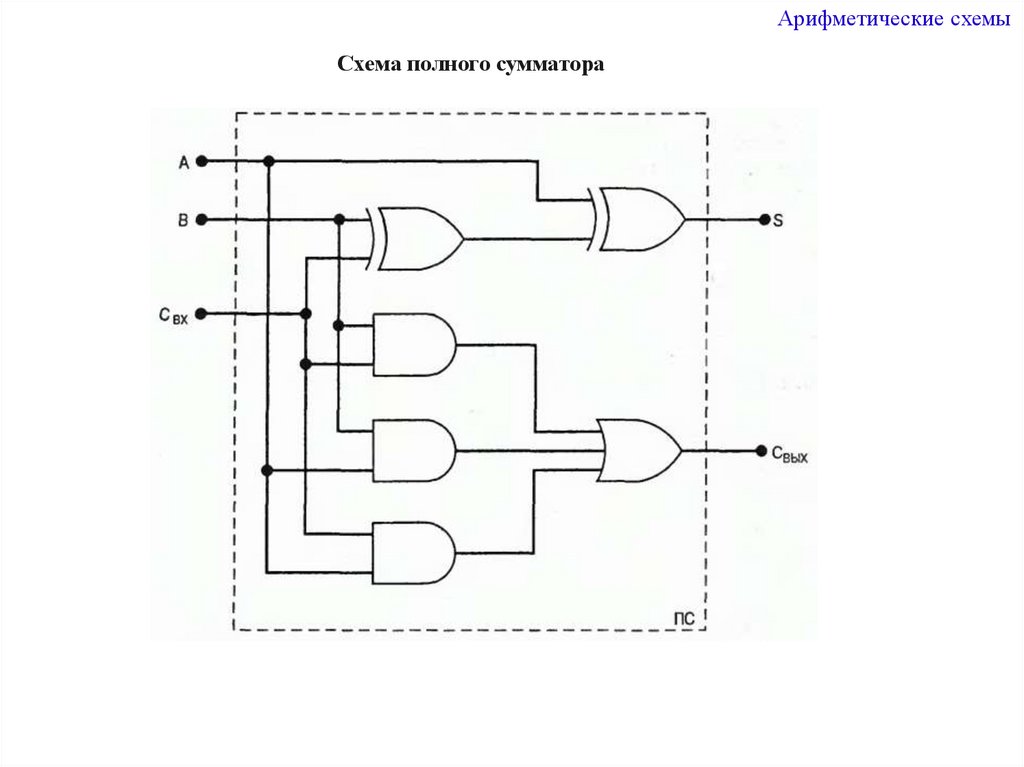
6.

Арифметические схемы
Схема полного сумматора

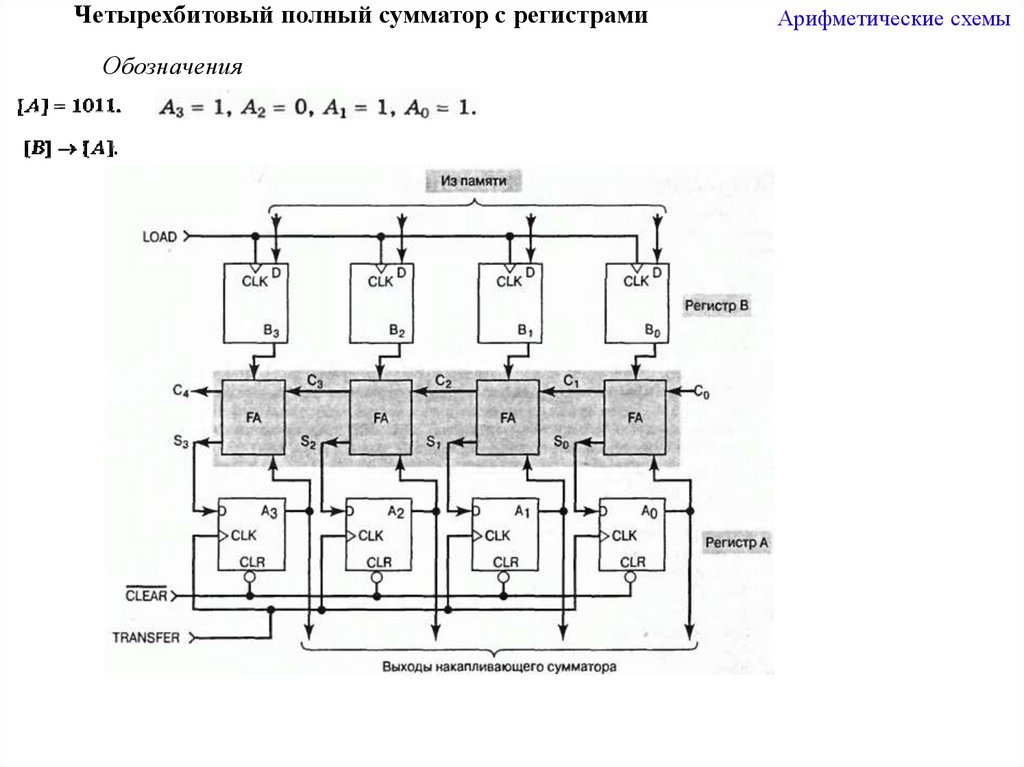
7.

Четырехбитовый полный сумматор с регистрами
Обозначения
Арифметические схемы

8.

Арифметические схемы

9.

Задержка сигнала переноса
Арифметические схемы
Сложение МЗБ этих чисел приводит к появлению переноса в следующий
разряд. Сложенный с битами второго разряда, бит переноса производит
новый перенос уже в третий разряд. То же самое повторяется и в третьей
позиции. Ключевым моментом выступает тот факт, что на бит суммы,
который появился после сложения последних разрядов (СЗБ) обоих чисел,
повлиял перенос, полученный при сложении первых разрядов (МЗБ).
Бит S3, снимаемый с последнего полного сумматора, зависит от бита переноса C1 с первого сумматора. Однако при
этом сигнал C1 должен пройти три полных сумматора прежде, чем он достигнет четвертого и приведет к появлению
бита S3. Это означает, что на выходе S3 не может появиться правильное значение, пока сигнал C1 не пройдет
промежуточные сумматоры. Такое условие приводит к появлению временной задержки, которая зависит от задержек
распространения, создаваемых сумматорами. Например, если задержка распространения у каждого полного
сумматора будет составлять 40 нс, то на выходе S3 правильное значение появится не раньше, чем через 120 нс после
формирования бита. Таким образом, результат сложения не может быть снят с выхода схемы ранее, чем через 160 нс
от момента, когда первое и второе слагаемые появятся на триггерах регистров (дополнительная задержка на 40 нс
вызвана тем, что следует также учесть задержку в полном сумматоре МЗБ, который формирует бит С1).
Естественно, что при расширении схемы параллельного сумматора для сложения большего количества битов эта
ситуация только ухудшится. Если бы подобный сумматор должен был складывать 32-битовые числа, то задержка
распространения сигнала переноса достигла бы 1280нс = 1,28 мкс. Результат нельзя получить ранее, чем через 1,28
мкс после записи исходных чисел в регистры.
Такая величина задержки препятствует созданию высокоскоростных устройств. Несмотря на это разработчики
логических устройств пришли к новому решению в виде оригинальных схем с уменьшенной задержкой. Одно из
таких решений называется ускоренным переносом, а схема, использующая такое нововведение, имеет в своем
составе дополнительные логические элементы, которые позволяют определить наличие переноса в старшие разряды
при сложении младших разрядов.

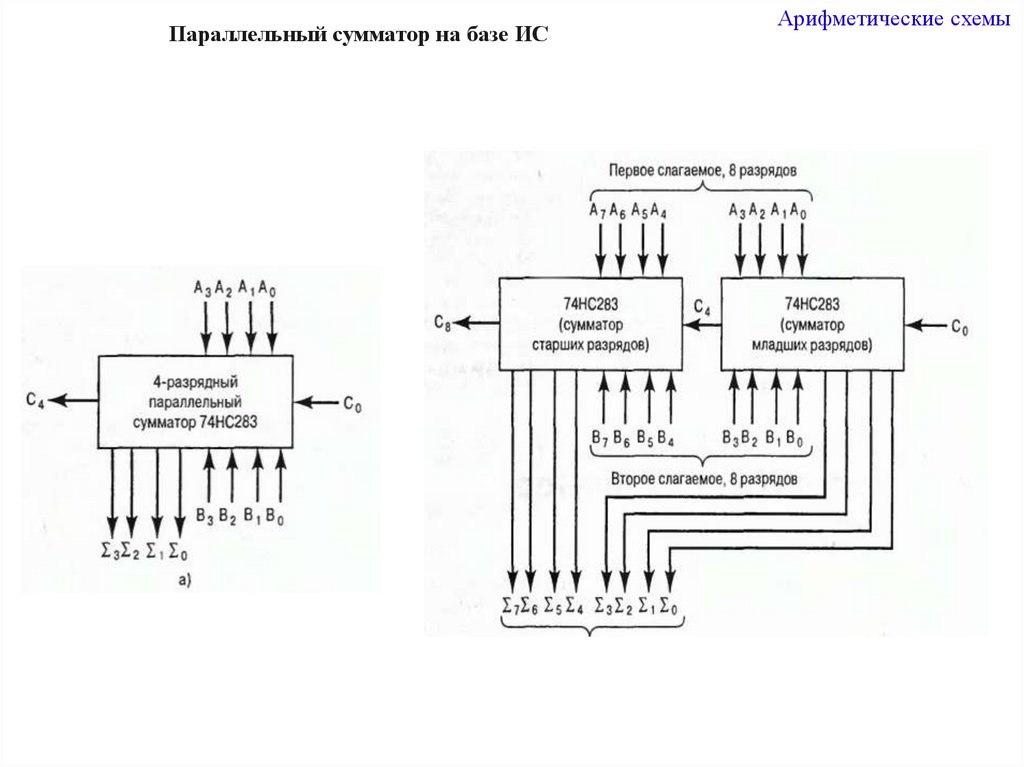
10.

Параллельный сумматор на базе ИС
Арифметические схемы

11.

Схемы для работы с дополнительными кодами
Сложение отрицательного и положительного числа
Арифметические схемы

12.

Вычитание положительного числа из положительного
Арифметические схемы

13.

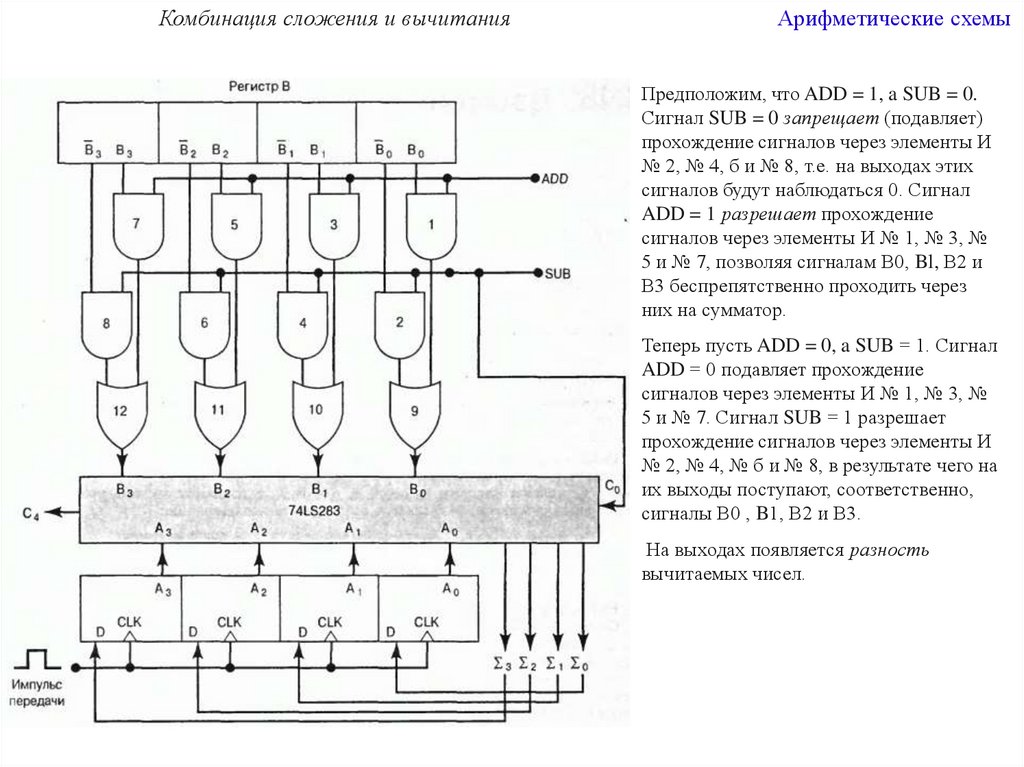
Комбинация сложения и вычитания
Арифметические схемы
Предположим, что ADD = 1, a SUB = 0.
Сигнал SUB = 0 запрещает (подавляет)
прохождение сигналов через элементы И
№ 2, № 4, б и № 8, т.е. на выходах этих
сигналов будут наблюдаться 0. Сигнал
ADD = 1 разрешает прохождение
сигналов через элементы И № 1, № 3, №
5 и № 7, позволяя сигналам В0, Bl, В2 и
В3 беспрепятственно проходить через
них на сумматор.
Теперь пусть ADD = 0, a SUB = 1. Сигнал
ADD = 0 подавляет прохождение
сигналов через элементы И № 1, № 3, №
5 и № 7. Сигнал SUB = 1 разрешает
прохождение сигналов через элементы И
№ 2, № 4, № б и № 8, в результате чего на
их выходы поступают, соответственно,
сигналы В0 , B1, В2 и В3.
На выходах появляется разность
вычитаемых чисел.

14.

Двоично-десятичный сумматор
Арифметические схемы

15.

Арифметические схемы

16.

Арифметические схемы
Сумма S4S3S2S1S0 может лежать в диапазоне от 00000 до 10010 (в том случае, если обе
кодовые группы равны 1001 = 9). Схема двоично-десятичного сумматора должна включать
логические элементы, необходимые для обнаружения ситуации, когда сумма превышает число
01001, т.е. когда требуется коррекция результата. Случаи, когда сумма превышает 01001,
приведены в табл. Теперь введем переменную X для обозначения логического сигнала, который
становится высоким только в том случае, если сумма превышает 01001 (т.е. в случаях,
записанных в табл.).
Если внимательно изучить эти ситуации, то можно увидеть, что сигнал X становится высоким
при выполнении хотя бы одного из приведенных ниже условий:

17.

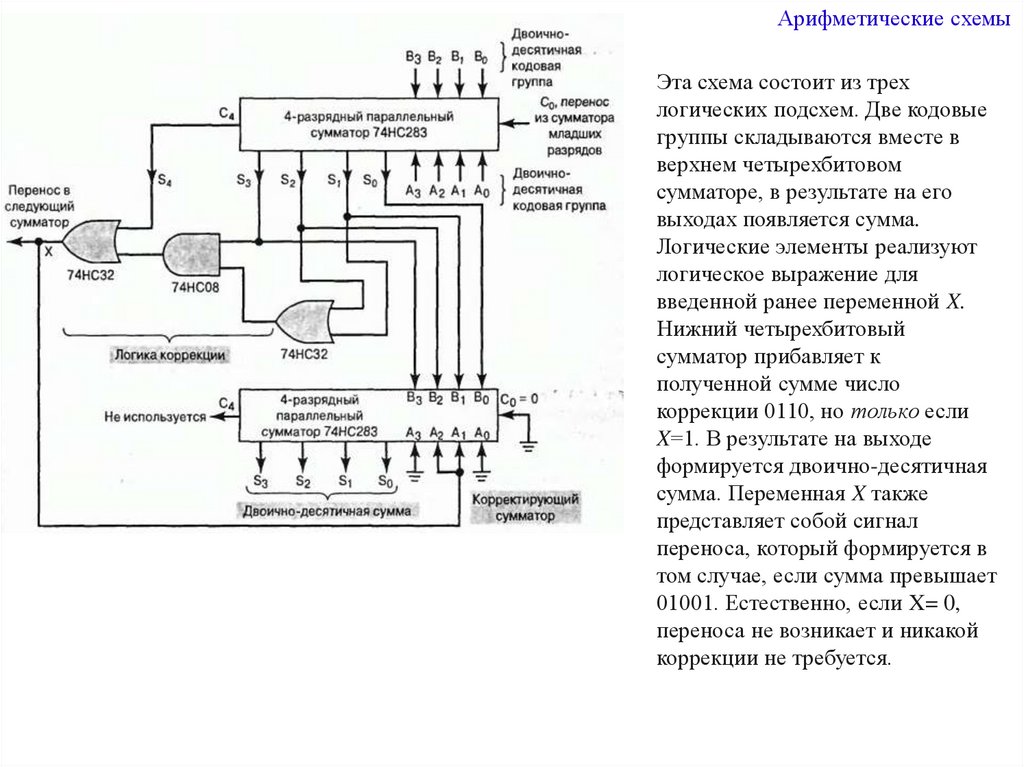
Арифметические схемы
Эта схема состоит из трех
логических подсхем. Две кодовые
группы складываются вместе в
верхнем четырехбитовом
сумматоре, в результате на его
выходах появляется сумма.
Логические элементы реализуют
логическое выражение для
введенной ранее переменной X.
Нижний четырехбитовый
сумматор прибавляет к
полученной сумме число
коррекции 0110, но только если
X=1. В результате на выходе
формируется двоично-десятичная
сумма. Переменная X также
представляет собой сигнал
переноса, который формируется в
том случае, если сумма превышает
01001. Естественно, если X= 0,
переноса не возникает и никакой
коррекции не требуется.

18.

Последовательное соединение двоично-десятичных сумматоров
Арифметические схемы

19.

Арифметические схемы

20.

Арифметические схемы

21.

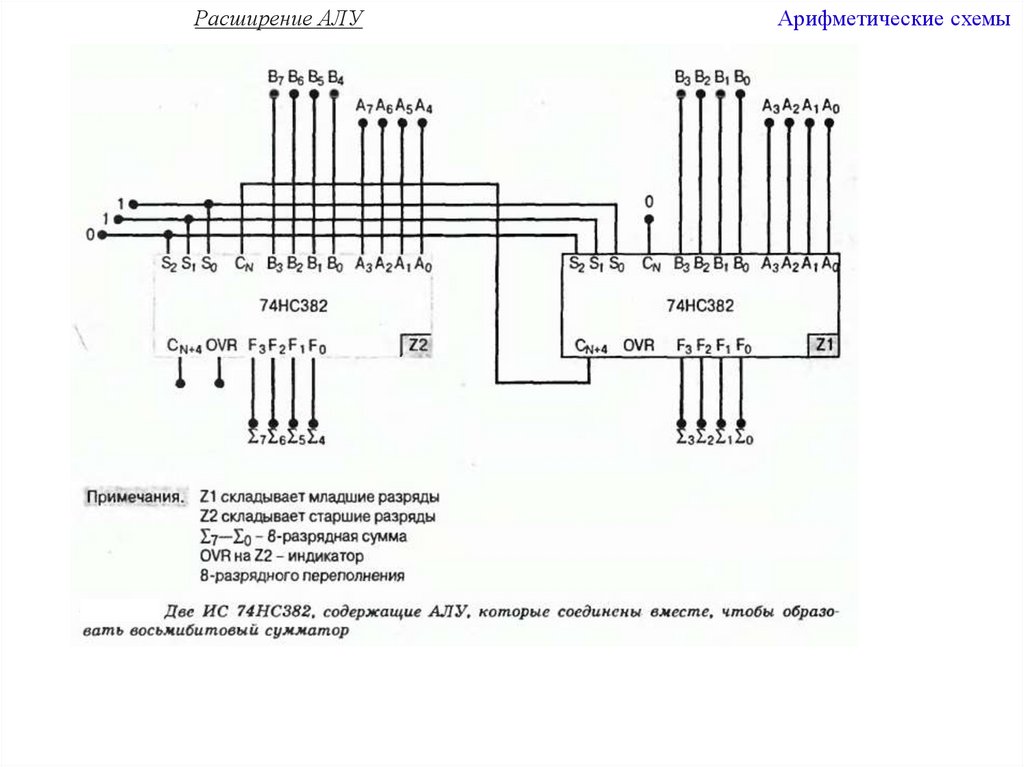
Расширение АЛУ
Арифметические схемы

22.

Арифметические схемы

23.

Задание!!!
Арифметические схемы