Дисперсия звука

1.

Дисперсия звука
Трофимов Н.С

2.

Постановка задачи
Объяснить природу возникновения аномальной дисперсии звука,
которую можно услышать, например, на следующих видео:

3.

Качественное объяснение
Если чуть лучше вслушаться в звуки на видео, то можно понять,
что мы слышим совсем не типичный звук удара. Сначала мы
слышим волны большой частоты, а потом низкой. Значит
виновником является дисперсия.
Как мы знаем, в неограниченной и однородной среде
дисперсия (зависимость скорости распространения от частоты)
звуковых волн отсутствует. Иначе люди, например, пришедшие на
концерт, слышали с задних рядов лишь хаотичный набор звуков
вместо музыки. Можно сделать заключение, что это явление
связано с тем, что у этих объектов хотя бы один размер много
больше другого.

4.

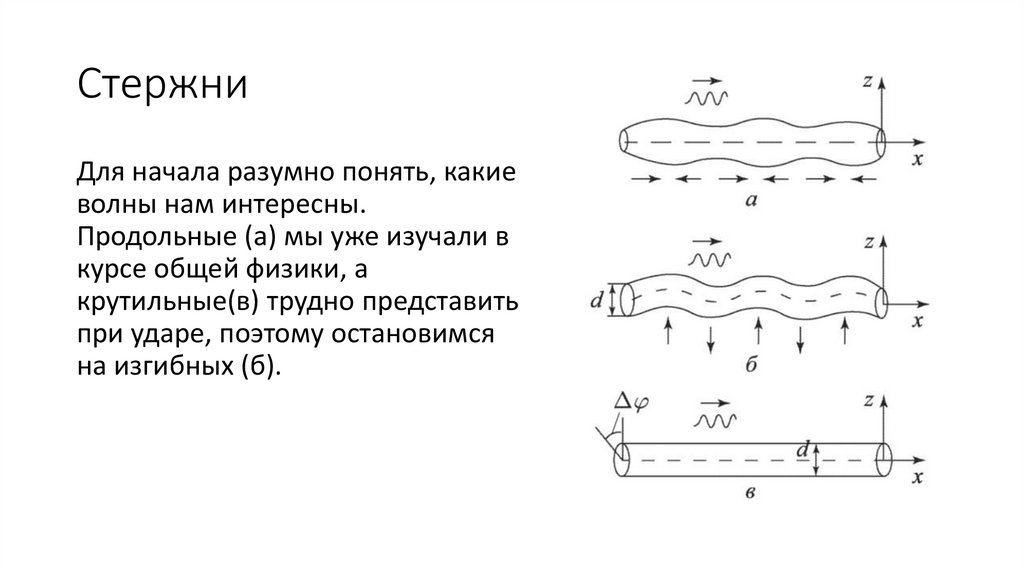
Стержни
Для начала разумно понять, какие
волны нам интересны.
Продольные (а) мы уже изучали в
курсе общей физики, а
крутильные(в) трудно представить
при ударе, поэтому остановимся
на изгибных (б).

5.

Немного про вывод волнового уравнения
(подробно написан в работе)
Упрощения:
Поперечные сечения стержня, плоские и перпендикулярные его оси,
во время изгиба остаются плоскими и перпендикулярными
деформированной оси стержня; продольные сечения стержня
сопротивляются изгибу независимо, не оказывая друг на друга
влияния; пренебрегаем угловым "ускорением кусочков" стержня.
Здесь I - осевой момент инерции
поперечного сечения стержня
(относительно оси
перпендикулярной x, лежащей в
плоскости uOx

6.

Дисперсионное уравнение и групповая скорость
Далее подставим в уравнение гармоническую бегущую волну и
получим:
Далее нам нужно найти групповую скорость, т.е. скорость распространения волнового пакета волн с
близкими частотами и волновыми числами. Если сложить две волны, то можно получить:

7.

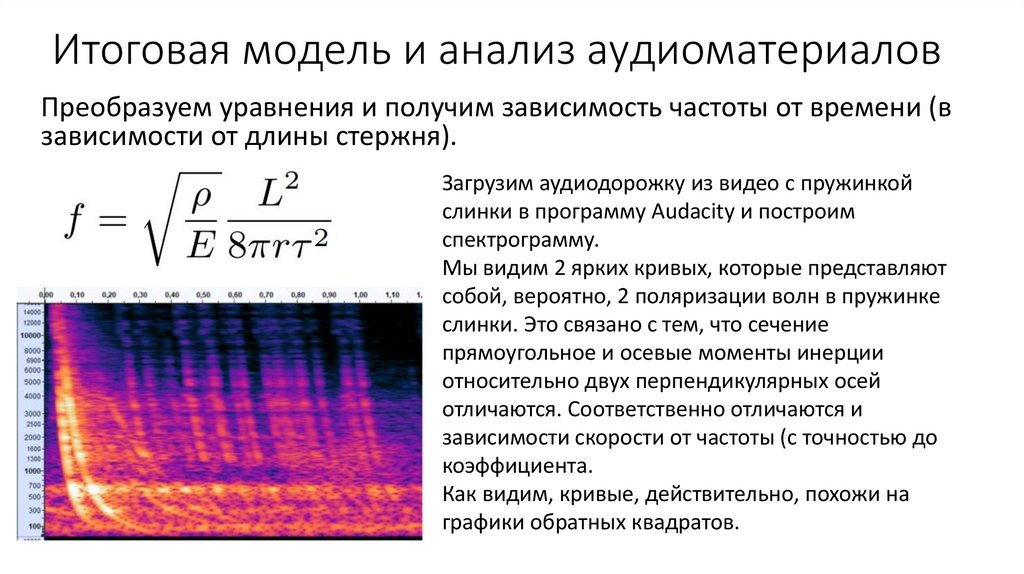
Итоговая модель и анализ аудиоматериалов
Преобразуем уравнения и получим зависимость частоты от времени (в
зависимости от длины стержня).
Загрузим аудиодорожку из видео с пружинкой
слинки в программу Audacity и построим
спектрограмму.
Мы видим 2 ярких кривых, которые представляют
собой, вероятно, 2 поляризации волн в пружинке
слинки. Это связано с тем, что сечение
прямоугольное и осевые моменты инерции
относительно двух перпендикулярных осей
отличаются. Соответственно отличаются и
зависимости скорости от частоты (с точностью до
коэффициента.
Как видим, кривые, действительно, похожи на
графики обратных квадратов.

8.

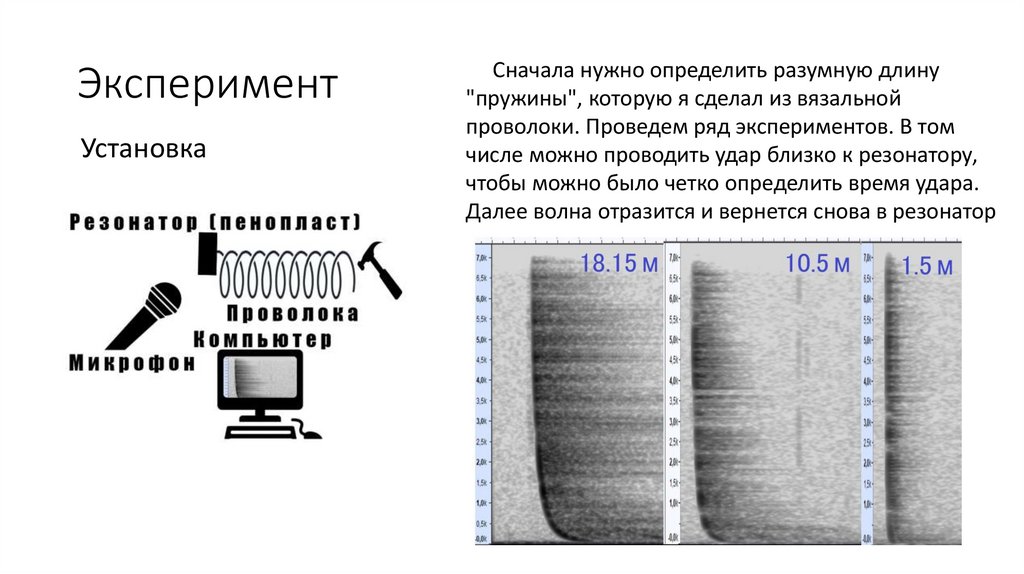
Эксперимент
Установка
Сначала нужно определить разумную длину
"пружины", которую я сделал из вязальной
проволоки. Проведем ряд экспериментов. В том
числе можно проводить удар близко к резонатору,
чтобы можно было четко определить время удара.
Далее волна отразится и вернется снова в резонатор

9.

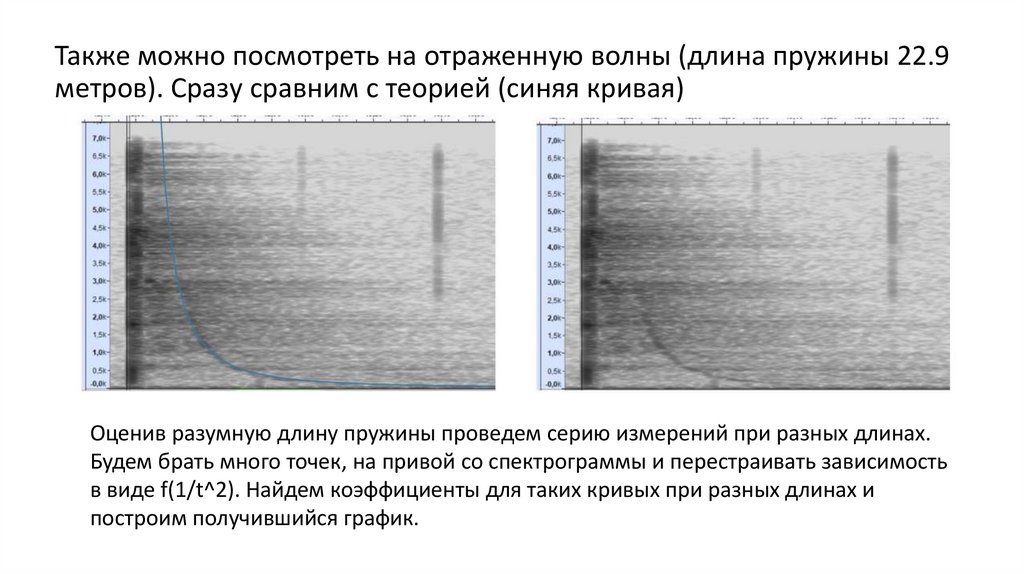
Также можно посмотреть на отраженную волны (длина пружины 22.9
метров). Сразу сравним с теорией (синяя кривая)
Оценив разумную длину пружины проведем серию измерений при разных длинах.
Будем брать много точек, на привой со спектрограммы и перестраивать зависимость
в виде f(1/t^2). Найдем коэффициенты для таких кривых при разных длинах и
построим получившийся график.

10.

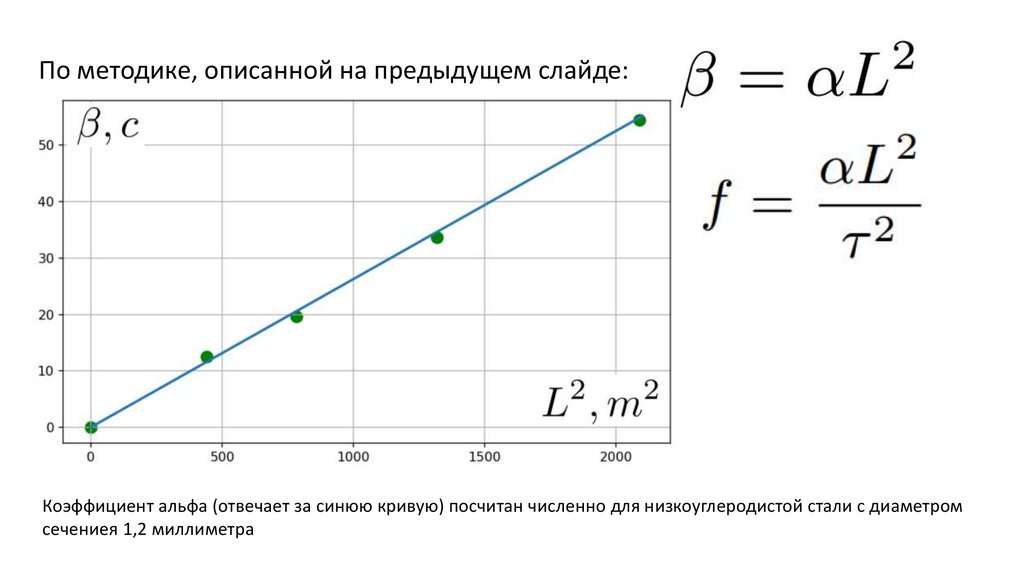
По методике, описанной на предыдущем слайде:
Коэффициент альфа (отвечает за синюю кривую) посчитан численно для низкоуглеродистой стали с диаметром
сечениея 1,2 миллиметра

11.

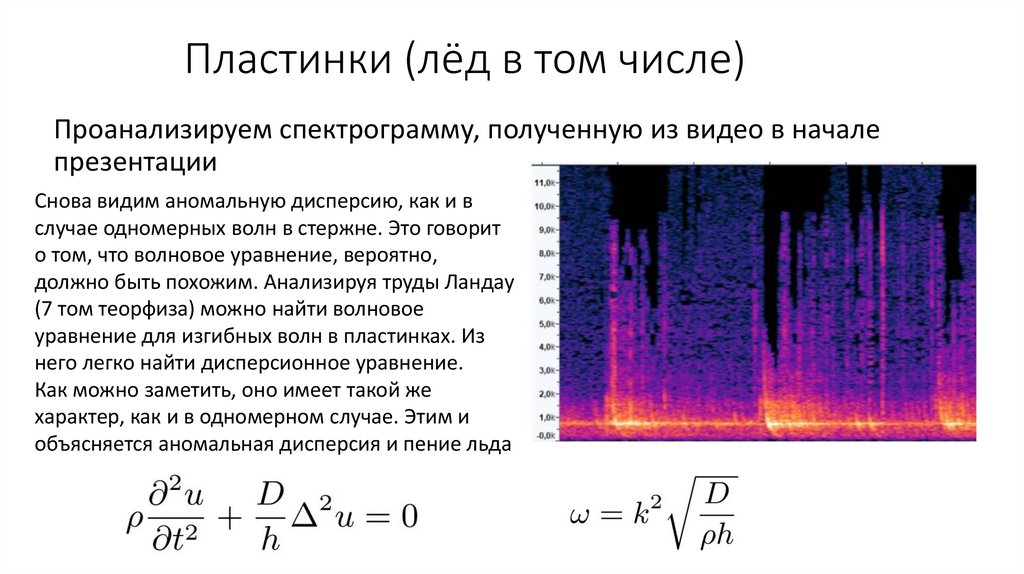
Пластинки (лёд в том числе)
Проанализируем спектрограмму, полученную из видео в начале
презентации
Снова видим аномальную дисперсию, как и в
случае одномерных волн в стержне. Это говорит
о том, что волновое уравнение, вероятно,
должно быть похожим. Анализируя труды Ландау
(7 том теорфиза) можно найти волновое
уравнение для изгибных волн в пластинках. Из
него легко найти дисперсионное уравнение.
Как можно заметить, оно имеет такой же
характер, как и в одномерном случае. Этим и
объясняется аномальная дисперсия и пение льда

12.

Подведение итогов
• Построили теоретическую модель, с помощью которой смогли
описать явление дисперсии звуковых волн в стержне. Успешно
провели эксперимент, который подтверждает построенную
модель (небольшие оговорки).
• В случае пластинок качественно объяснили явление и
проанализировали спектрограмму.

13.

Спасибо за внимание.