Similar presentations:
Умножение и деление обыкновенных дробей
1.
Умножение и делениеобыкновенных дробей
2.
Умножение дробей на натуральное число7
9
7
9
7
9
7
9
7
7 7 7 7 7 + 7 + 7 + 7 7 ∙ 4 28
∙4= + + + =
=
=
9
9
9
9
9 9 9 9
Чтобы умножить дробь на натуральное число, надо
ее числитель умножить на это число, а знаменатель
оставить без изменения.
3.
Умножение дробей на дробь4
5
Найти S закрашенной фигуры
2
3
8
S=
15
S=a∙b
2 4 2∙4 8
S=
∙
=
=
3 5 3 ∙ 5 15
Чтобы умножить дробь на дробь, надо: 1) найти
произведение числителей и произведение
знаменателей этих дробей; 2) первое произведение
записать числителем, а второе – знаменателем.
4.
Попробуем вместе:1
1 12 12
12
3
4
4
4
1
2
1
3
5 14 5 14 1 2 2
7 15 7 15 1 3 3
5.
Умножение смешанных чисел4
3 1 11 16 11 16 11 4 44
4
2 3
8
4 5 4 5
4 5
1 5
5
5
1
13
4
3
1
2 2 65 12 65 12 13 4 52
1
7 2
17
9 5 9 5
9 5
3 1
3
3
Для того чтобы выполнить умножение смешанных
чисел, надо их записать в виде неправильных дробей, а
затем воспользоваться правилом умножения дробей.
6.
7.
8.
27.12.23Классная работа
Умножение и деление
обыкновенных дробей
9.
10.
11.
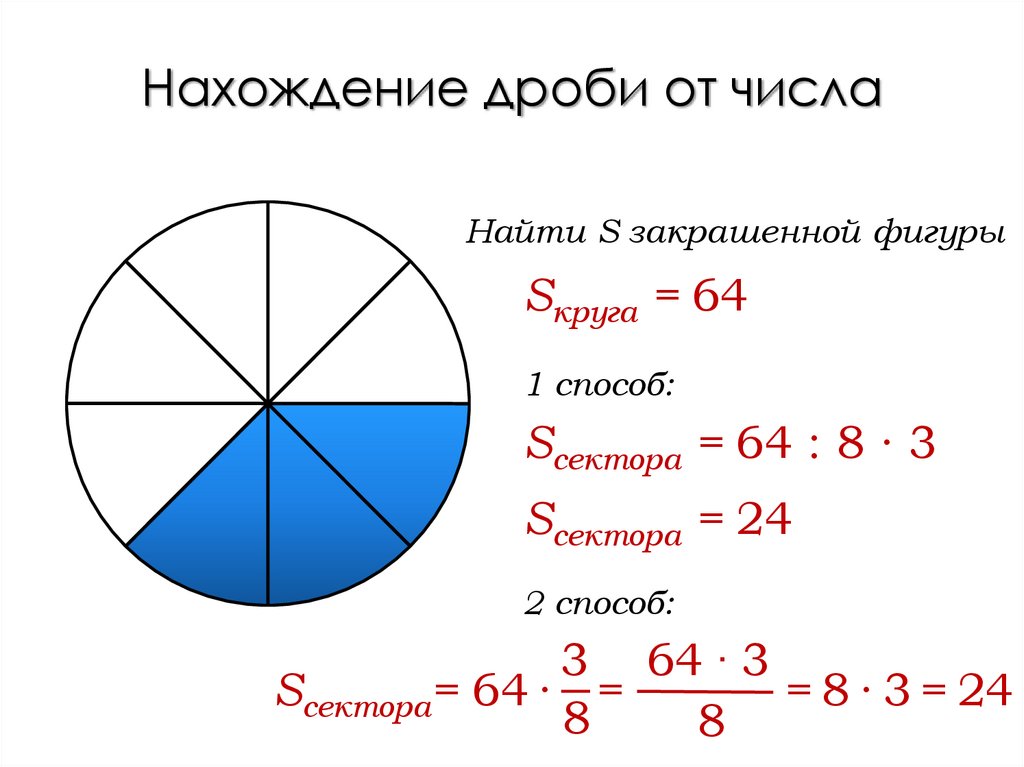
Нахождение дроби от числаНайти S закрашенной фигуры
Sкруга = 64
1 способ:
Sсектора = 64 : 8 ∙ 3
Sсектора = 24
2 способ:
3 64 ∙ 3
Sсектора= 64 ∙ =
= 8 ∙ 3 = 24
8
8
12.
Нахождениедроби
отот
числа
Нахождение
дроби
числа
3
Найти
от 48
4
12
3
3 48 3 12
48
36
4
4
1
1
Чтобы найти дробь от числа, нужно умножить число
на эту дробь.
13.
Нахождениедроби
от
числа
Нахождение дроби от числа
5
Найти
от 0,28
7
1
4
1
5
5 28
5 28
1 4 1
0,28
7
7 100 17 10020 1 205 5
Чтобы найти дробь от числа, нужно умножить число
на эту дробь.
14.
Применение распределительногосвойства умножения
a b c ac bc
a b c ac bc
15.
Применение распределительного свойства умножения5
5
5
2 18 2 18 2 18 18
9
9
9
2
5 18
36
36 10 46
9
1
Чтобы умножить смешанное число на натуральное
число, можно:
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
3) сложить полученные результаты.
16.
Применение распределительного свойства умножения4
3
2
3
2 12 3 12
2 3
12 12 12
3
4
3
4
3 4
1
1
8 9 17
17.
Взаимно обратные числа5 9 5 9
1;
9 5 9 5
5 9 23 9
2
1;
9 23 9 23
1
1 8
8
1;
8
8
4
3 4 11
2
1.
11 4 11 4
Два числа, произведение которых равно 1, называют
взаимно обратными.
18.
Взаимно обратныеобратные числа
числа
Взаимно
a b a b
1;
b a b a
1
1 а 1 а
а
1;
а
а 1 а 1
а 0; b 0.
Два числа, произведение которых равно 1, называют
взаимно обратными.
19.
Деление дроби на натуральное чилоЧтобы поделить натуральное число на дробь, следует число
умножить на дробь обратную заданной.
3
4 4 4 16
1
4 4
5
4
3
3
3
3
Чтобы поделить дробь на натуральное число,
следует знаменатель дроби умножить на число.
4
4 3 4 1 4
3
7
7 1 7 3 21
4
4
4
3
7
7 3 21
или
20.
Деление дробей и смешанных чиселЧтобы поделить натуральное число на дробь, следует число
умножить на дробь обратную заданной.
3
4 4 4 16
1
4 4
5
4
3
3
3
3
Чтобы поделить дробь на натуральное число,
следует знаменатель дроби умножить на число.
4
4 3 4 1 4
3
7
7 1 7 3 21
4
4
4
3
7
7 3 21
или
21.
Деление1
3
2 8 2 9 2 9 1 3 3
:
;
3 9 3 8 13 8 4 1 4 4
4 1 9 13 9 4
9 4 36
1 :3 :
.
5 4 5 4 5 13 5 13 65
Чтобы разделить одну дробь на другую, надо делимое
умножить на число, обратное делителю.
22.
23.
24.
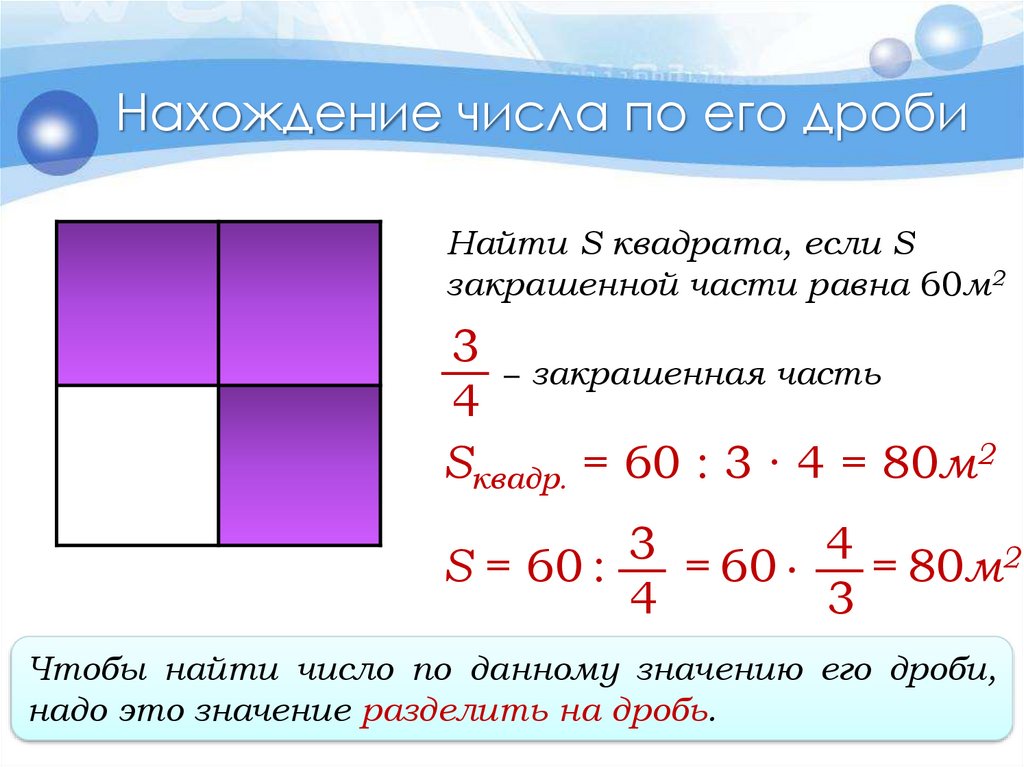
Нахождение числа по его дробиНайти S квадрата, если S
закрашенной части равна 60м2
3
− закрашенная часть
4
Sквадр. = 60 : 3 ∙ 4 = 80м2
3
4
S = 60 :
= 60 ∙
= 80м2
4
3
Чтобы найти число по данному значению его дроби,
надо это значение разделить на дробь.
25.
Нахождение числа по его дробиНайти число, если
3
его равны 48.
4
3 48 4
48 :
64;
4
3
Найти число, если
8
его равны 560.
9
8 560 9
560 :
630;
9
8
26.
Нахождение числа по его дробиНайти число, если 0,6 его равны 12,9.
12,9 : 0,6 129 : 6 21,5;
Найти число, если 35% его равны 91.
91 : 0,35 9100 : 35 260.
























 mathematics
mathematics








