Теорема Пифагора. Фрагмент урока геометрии

1.

ФРАГМЕНТ УРОКА ГЕОМЕТРИИ
8 КЛАСС
СОСТАВИЛА УЧИТЕЛЬ МАТЕМАТИКИ
ПАРТИЗАНСКОЙ СРЕДНЕЙ ШКОЛЫ
ИМЕНИ П. П. ПЕТРОВА
РЫЖОВА НАТАЛЬЯ ПЕТРОВНА

2. ТЕОРЕМА ПИФАГОРА

3. ЦЕЛИ :

1. ПОЗНАКОМИТЬСЯ С НОВЫМИ СПОСОБАМИ
ДОКАЗАТЕЛЬСТВА
2. УВИДЕТЬ ВОЗМОЖНОСТЬ ПРИМЕНЕНИЯ
ТЕОРЕМЫ НА ПРАКТИКЕ
3. РАСШИРИТЬ СВОЙ КРУГОЗОР

4. ПИФАГОР

ДОМОЙ
ЗНАМЕНИТЫЙ ГРЕЧЕСКИЙ
ФИЛОСОФ И МАТЕМАТИК
ПИФАГОР РОДОМ ИЗ
САМОСА ЖИЛ ОКОЛО 2,5
ТЫСЯЧ ЛЕТ ТОМУ НАЗАД
МНОГО ПУТЕШЕСТВОВАЛ,
БЫЛ В ИНДИИ , ЕГИПТЕ,
ВАВИЛОНЕ, ИЗУЧАЯ
КУЛЬТУРУ И ДОСТИЖЕНИЯ
НАУКИ РАЗНЫХ СТРАН
С ЕГО ИМЕНЕМ СВЯЗАНО
МНОГО ЛЕГЕНД. В ЧЕСТЬ
СВОЕГО ОТКРЫТИЯ ОН
ПРИНЕС В ЖЕРТВУ СТО
БЫКОВ

5. ЛЕГЕНДА

Пребудет вечной истина , как
скоро.
Все познает слабый человек !
И ныне теорема Пифагора
Верна , как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За свет луча, пришедший с
облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет
Быки ревут , ее почуя , вслед.
От страха , что вселил в них
Пифагор .
ДОМОЙ
А.Шамиссо

6.

•Считалось,что до Пифагора теорема не была известна
• Еще за 1200 лет до Пифагора она встречалась в вавилонских
текстах , была известна и древним китайцам, и индусам.
•Таким образом Пифагор не открыл это свойство , а впервые
доказал его.
•И с глубокой древности математики находят все новые и новые
доказательства теоремы Пифагора. И теперь их около 150 .
ДОМОЙ

7.

ВО ВРЕМЕНА ПИФАГОРА ТЕОРЕМА ЗВУЧАЛА ТАК :
ПЛОЩАДЬ КВАДРАТА, ПОСТРОЕННОГО НА ГИПОТЕНУЗЕ
ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА , РАВНА СУММЕ
ПЛОЩАДЕЙ КВАДРАТОВ , ПОСТРОЕННЫХ НА ЕГО КАТЕТАХ.
С2 = а2 + а2
--Посмотрите на квадрат
построенного на гипотенузе
. --Из чего он состоит ?
а
--Посмотрите на квадраты
построенные на катетах
с
а
ДОМОЙ
--Из чего состоят
квадраты?
--Какие это треугольники ?
Квадрат построенный на
гипотенузе состоит из 4
треугольников. А квадраты
построенные на катетах
состоят из 2 треугольников

8.

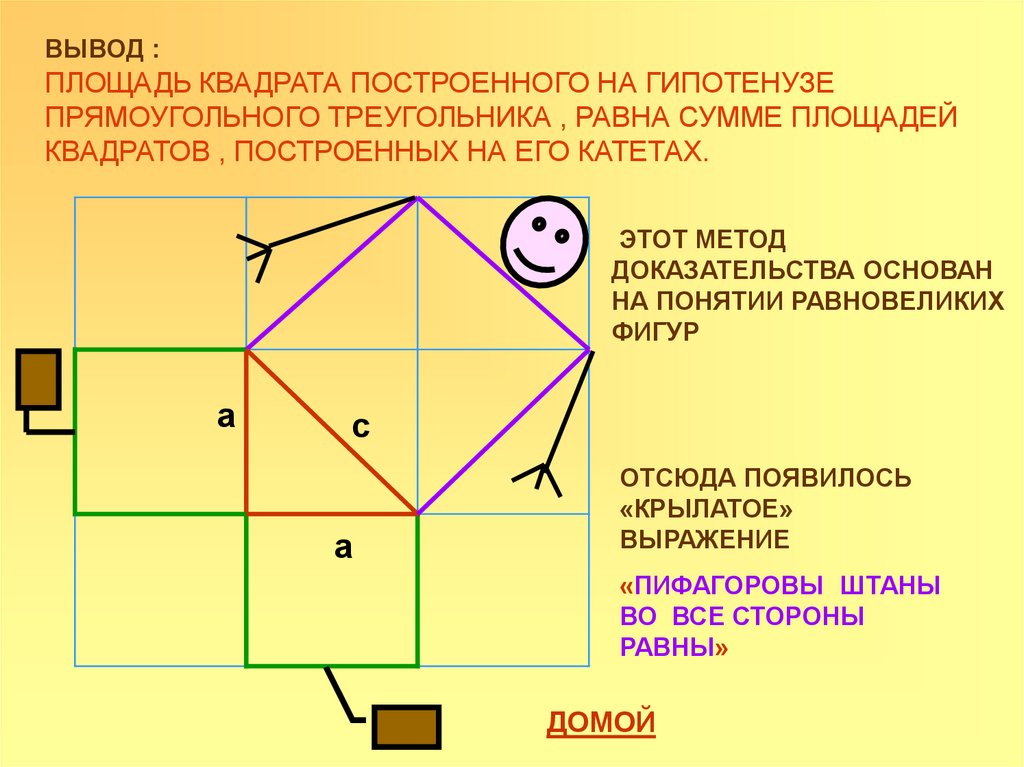
ВЫВОД :
ПЛОЩАДЬ КВАДРАТА ПОСТРОЕННОГО НА ГИПОТЕНУЗЕ
ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА , РАВНА СУММЕ ПЛОЩАДЕЙ
КВАДРАТОВ , ПОСТРОЕННЫХ НА ЕГО КАТЕТАХ.
ЭТОТ МЕТОД
ДОКАЗАТЕЛЬСТВА ОСНОВАН
НА ПОНЯТИИ РАВНОВЕЛИКИХ
ФИГУР
а
с
а
ОТСЮДА ПОЯВИЛОСЬ
«КРЫЛАТОЕ»
ВЫРАЖЕНИЕ
«ПИФАГОРОВЫ ШТАНЫ
ВО ВСЕ СТОРОНЫ
РАВНЫ»
ДОМОЙ

9.

Этот способ доказательства требует знания площадей
прямоугольника, прямоугольного треугольника,
квадрата и основан на перестановке фигур.
Как с помощью прямоугольника вывести формулу для вычисления площади прямоугольного треугольника ?
а
S=ab
s=ab/2
Такое рассуждение предложили древние индусы и
сопровождали чертеж одним словом « СМОТРИ ! »
в
s=(a+b)2- площадь большого квадрата
S=c2–
площадь маленького квадрата
Если от площади большого квадрата отнять
площади четырех прямоугольных
треугольников, то что получится ?
(a+b)2 – 4*ab/2 = c2
a2 + 2ab +b2 - 2ab = c2
ДОМОЙ
а
в
в
с
с
с
а
с
a2+ b2 =c2
а
в
в
а

10.

УЧАЩИЕСЯ СРЕДНИХ ВЕКОВ СЧИТАЛИ ДОКАЗАТЕЛЬСТВО
ТЕОРЕМЫ ОЧЕНЬ ТРУДНЫМ И ПРОЗВАЛИ ЕГО «ОСЛИНЫМ МОСТОМ»
ИЛИ «БЕГСТВОМ УБОГИХ» ,ТАК КАК СЛАБЫЕ УЧЕНИКИ БЕЖАЛИ ОТ
ГЕОМЕТРИИ. УЧАЩИЕСЯ РИСОВАЛИ ЗАБАВНЫЕ КАРИКАТУРЫ.

11.

ТЕОРЕМА ЗАНИМАЕТ В ГЕОМЕТРИИ ОСОБОЕ МЕСТО. НА ЕЕ ОСНОВЕ
МОЖНО ВЫВЕСТИ И ДОКАЗАТЬ БОЛЬШИНСТВО ТЕОРЕМ.
ДРУГИЕ СПОСОБЫ
ДОКАЗАТЕЛСТВА

12.

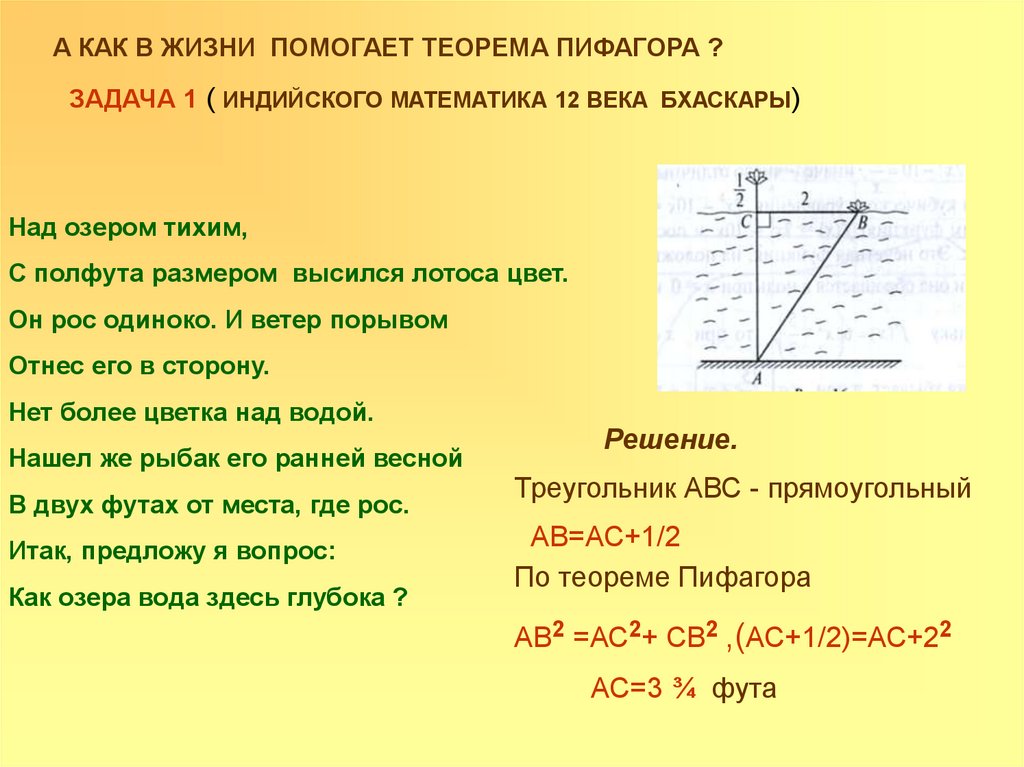
А КАК В ЖИЗНИ ПОМОГАЕТ ТЕОРЕМА ПИФАГОРА ?
ЗАДАЧА 1 ( ИНДИЙСКОГО МАТЕМАТИКА 12 ВЕКА БХАСКАРЫ)
Над озером тихим,
С полфута размером высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону.
Нет более цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока ?
Решение.
Треугольник АВС - прямоугольный
АВ=АС+1/2
По теореме Пифагора
АВ2 =АС2+ СВ2 ,(АС+1/2)=АС+22
АС=3 ¾ фута

13.

Задача 2
Этот эпизод из реальной следственной практики. Получив
сообщение о краже, следователь выехал на место
происшествия. Потерпевший заявил, что грабитель проник в
дом через окно.
Х2 = 1,22 + 1,82
Х2= 4, 68
хм
1,2м
1,8 м
Х2 = 1,44 + 3,24
Х
2,1 (м)
Вопрос . Как можно преодолеть это
расстояние без какого-либо средства,
например лестницы. Поиски этих средств
не увенчались успехом. И тогда
следователь выдвинул версию « Может
это инсценировка ограбления».В ходе
дальнейшего расследования эта версия
подтвердилась. Так школьная геометрия
помогла следствию.

14. тест

1 Когда жил греческий ученый Пифагор ?
1) Около 2,5 тысяч лет назад ?
2) Около 550 лет назад
3) Около 2,5 миллионов лет назад
ОТВЕТ1
2 Что принес в жертву Пифагор в честь своего открытия ?
1) 100 коров
2) 100 баранов
3) 100 быков
ОТВЕТ2

15.

3 Как звучала теорема во времена Пифагора ?
1) В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов
2) Площадь квадрата построенного на гипотенузе
прямоугольного треугольника, равна сумме площадей
квадратов, построенных на его катетах
3) Пифагоровы штаны во все стороны равны
ОТВЕТ

16.

4 Сколько новых доказательств теоремы вы узнали ?
1) 3
2) 1
3) 2
ОТВЕТ1 ОТВЕТ2
5 Сколько всего доказательств теоремы Пифагора ?
1) Около 50
2) Около 150
3) Около 90
ОТВЕТ

17.

Мы должны быть благодарны Истории человечества,
которая не только подарила миру таких людей как Пифагор,
Евклид, Архимед, но и сохранила память о них.
Рафаэль. Афинская школа.