Решение геометрических задач (треугольники)

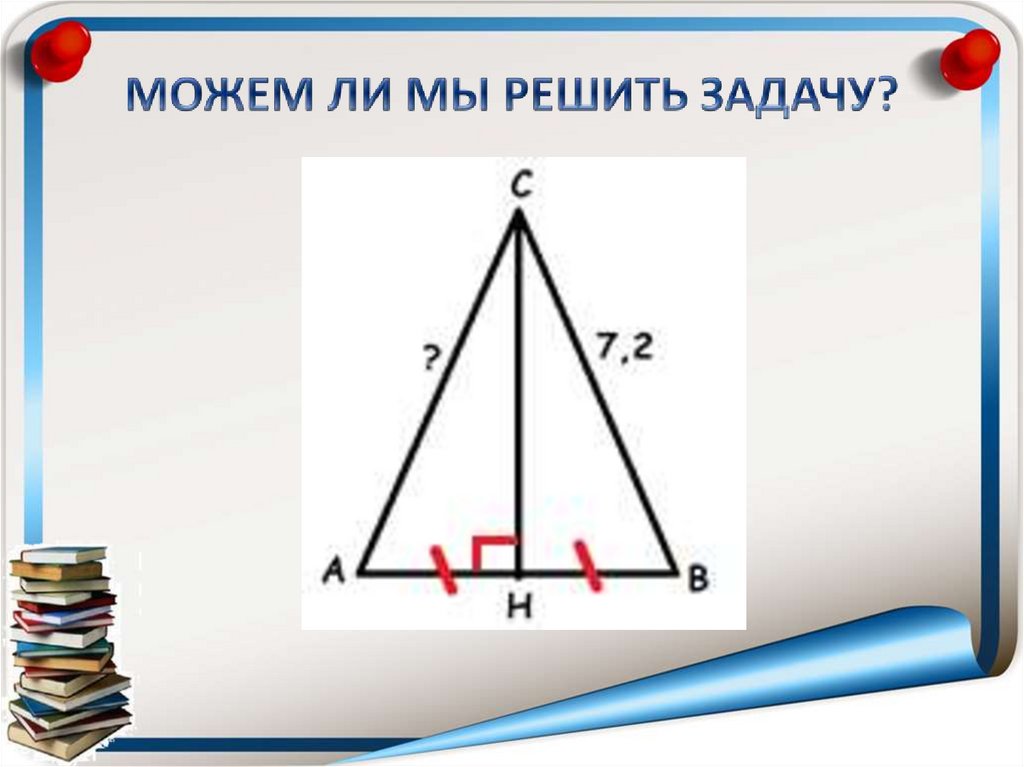
1.

2.

3.

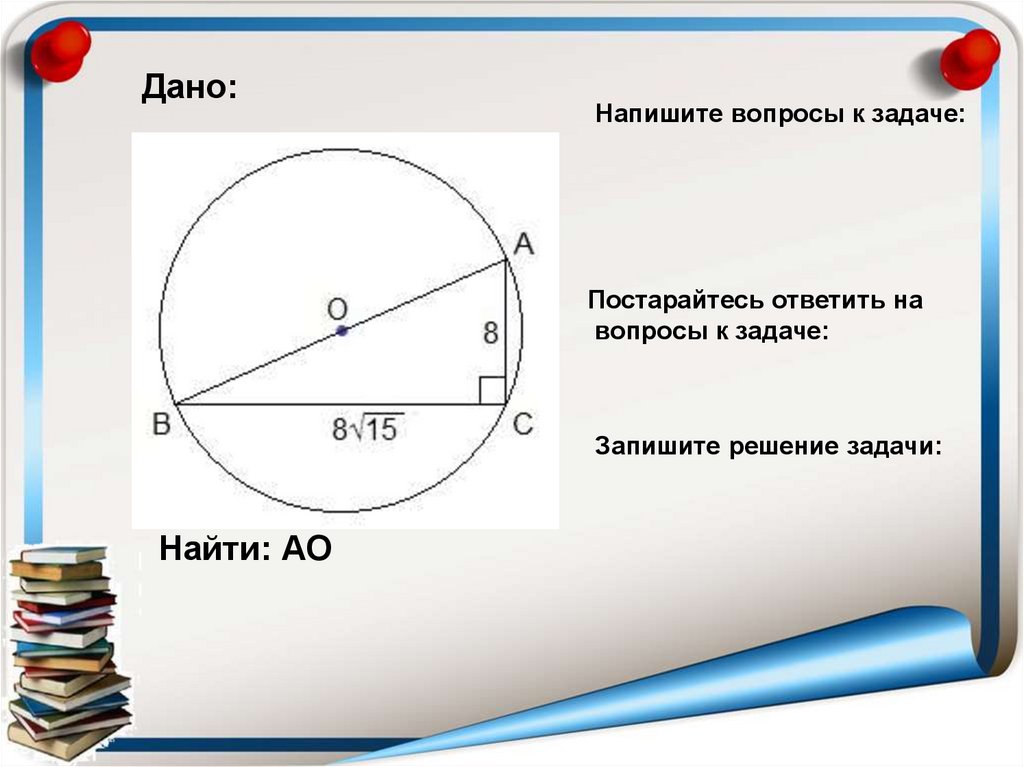
Дано:
Напишите вопросы к задаче:
Постарайтесь ответить на
вопросы к задаче:
Запишите решение задачи:
Найти: АО

4.

1. Выделить темы, имеющие место в
задании, через наводящие вопросы.
2. Найти в учебнике, справочной литературе
сведения по данной теме.
3. Повторить, выучить.
4. Приступить к решению.
Помните!
Нельзя решить задачу, не зная
свойств, определений понятий,
которые указаны в задаче.

5.

6.

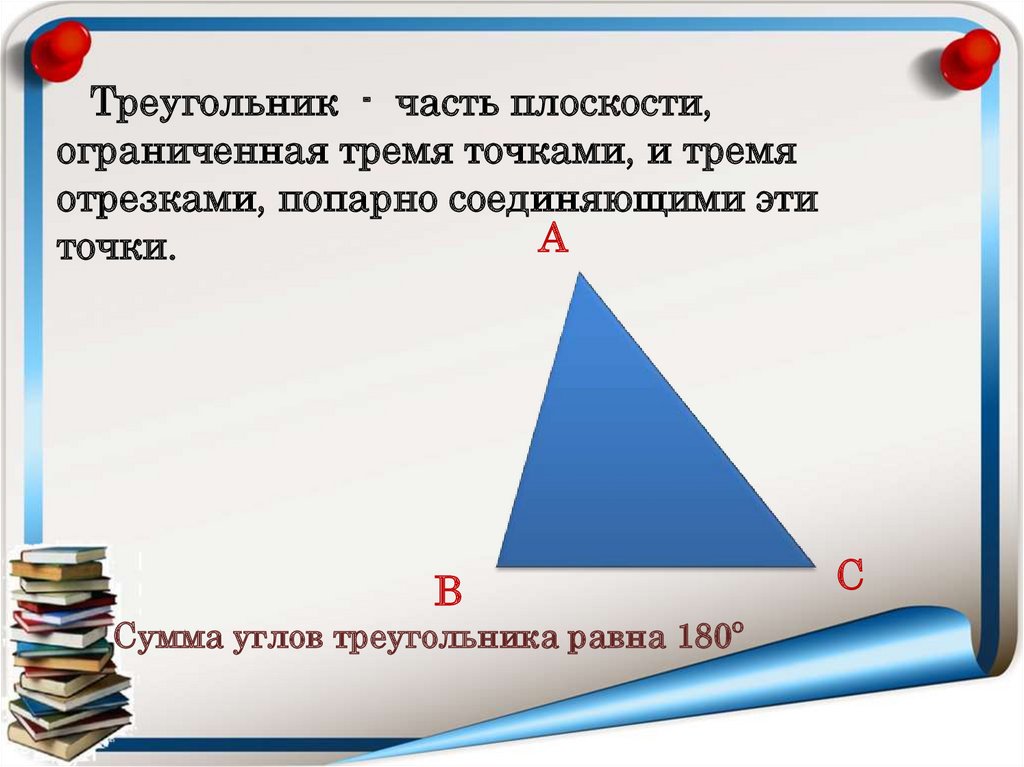
Треугольник - часть плоскости,
ограниченная тремя точками, и тремя
отрезками, попарно соединяющими эти
А
точки.
В
Сумма углов треугольника равна 180º
С

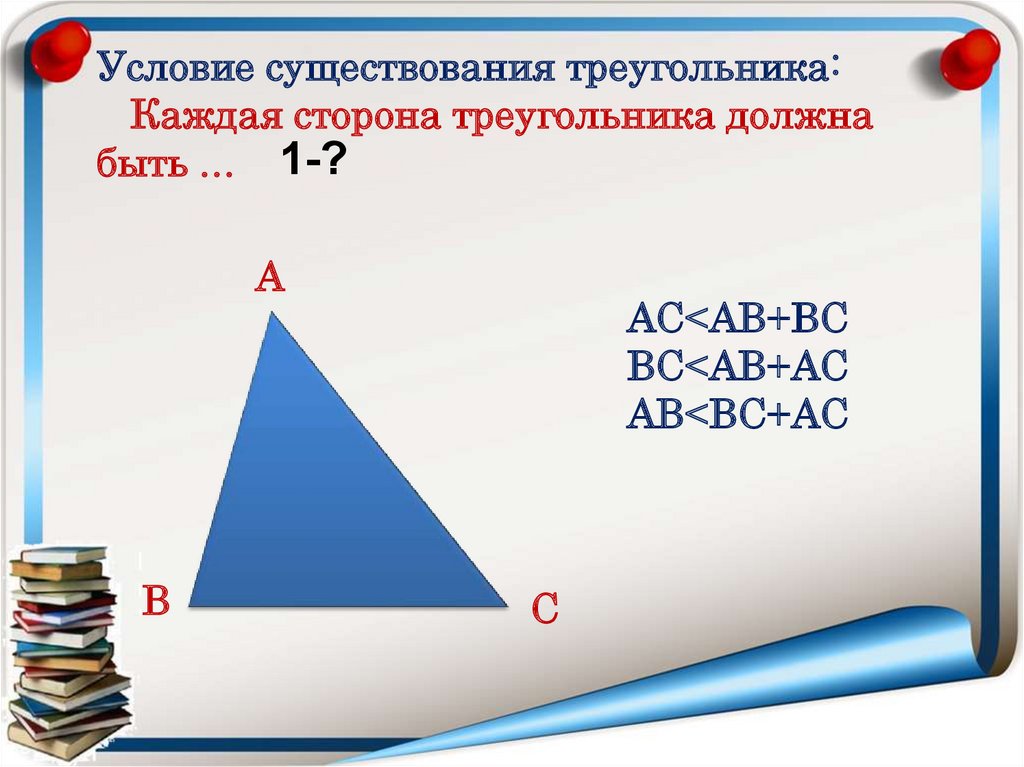
7.

Условие существования треугольника:
Каждая сторона треугольника должна
быть … 1-?
А
В
АС<АВ+ВС
ВС<АВ+АС
АВ<ВС+АС
С

8.

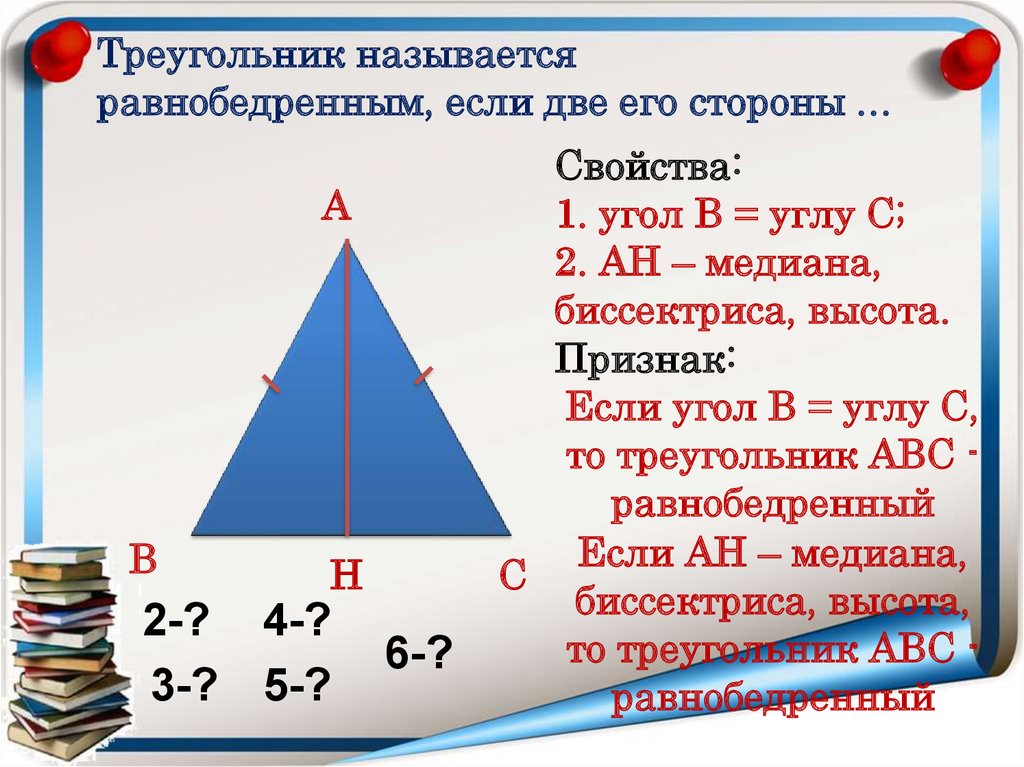
Треугольник называется
равнобедренным, если две его стороны …
А
В
Н
2-? 4-?
3-? 5-?
6-?
Свойства:
1. угол В = углу С;
2. АН – медиана,
биссектриса, высота.
Признак:
Если угол В = углу С,
то треугольник АВС равнобедренный
Если АН – медиана,
С
биссектриса, высота,
то треугольник АВС равнобедренный

9.

А
Треугольник, в котором один из
углов равен 90º, называется …
Сумма острых углов
прямоугольного треугольника
равна … градусов.
С
В
7-?
8-?

10.

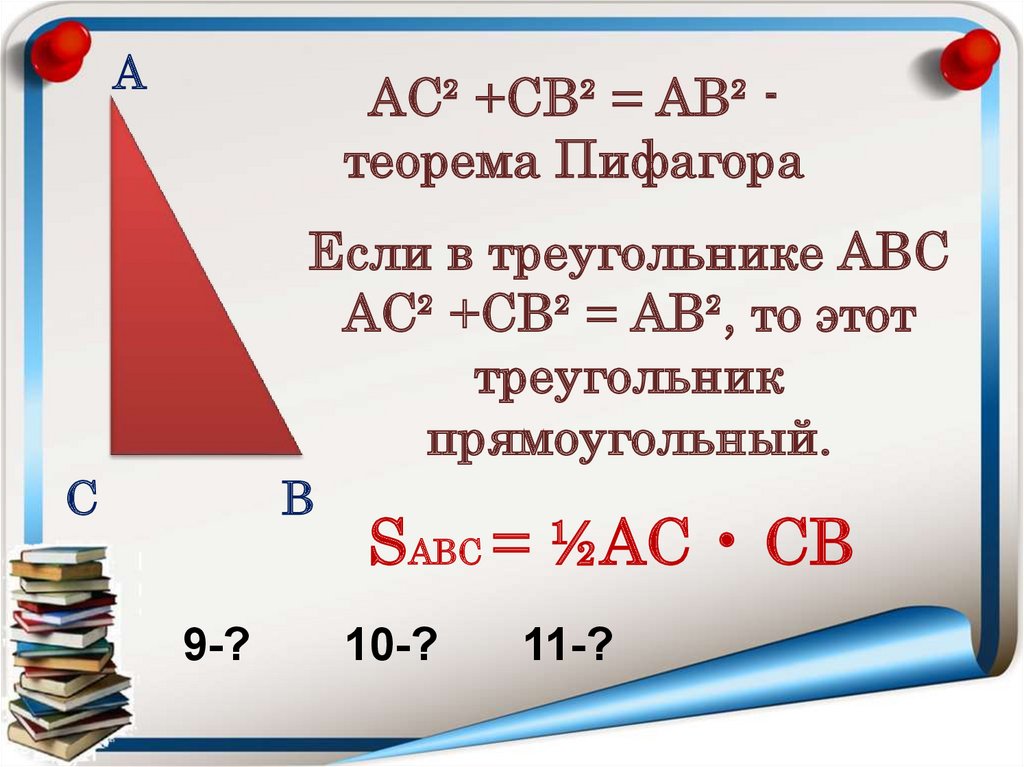
А
АС² +СВ² = АВ² теорема Пифагора
Если в треугольнике АВС
АС² +СВ² = АВ², то этот
треугольник
прямоугольный.
С
В
9-?
SАВС = ½АС • СВ
10-?
11-?

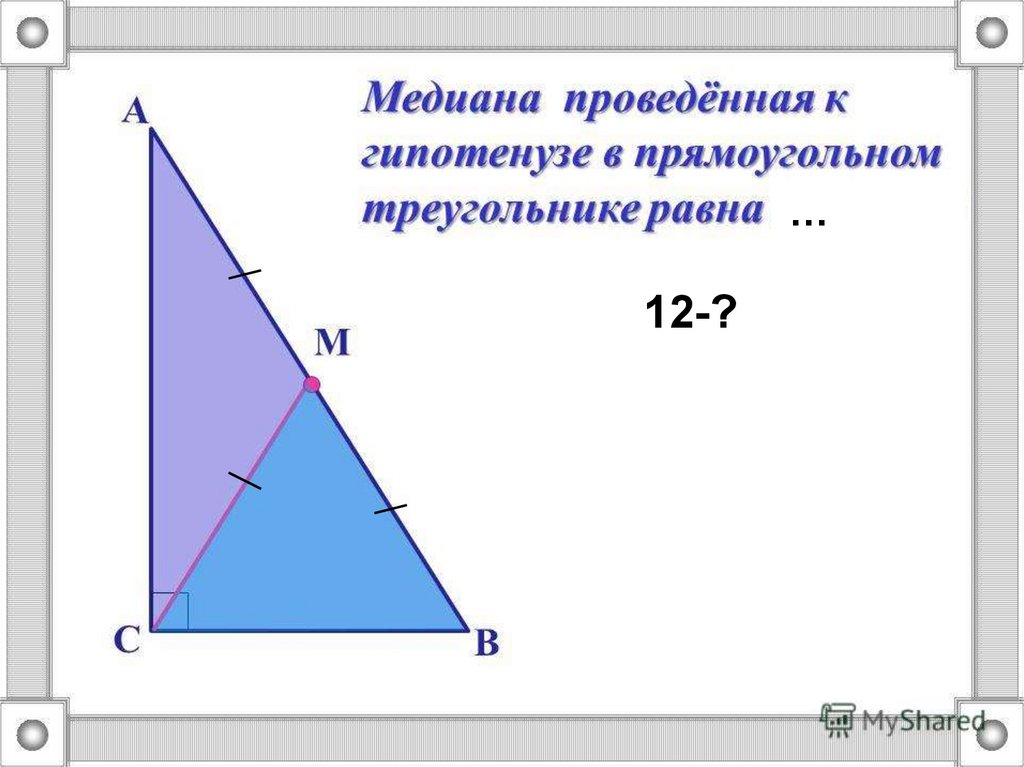
11.

…
12-?

12.

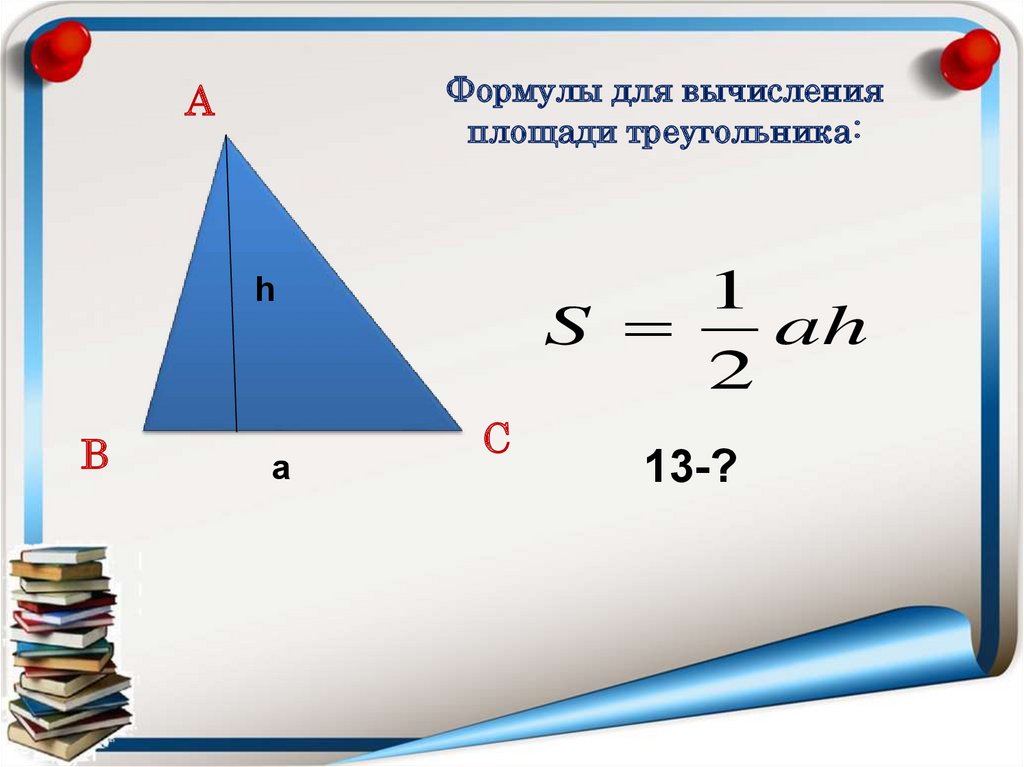
Формулы для вычисления
площади треугольника:
А
1
S
ah
2
h
В
a
С
13-?

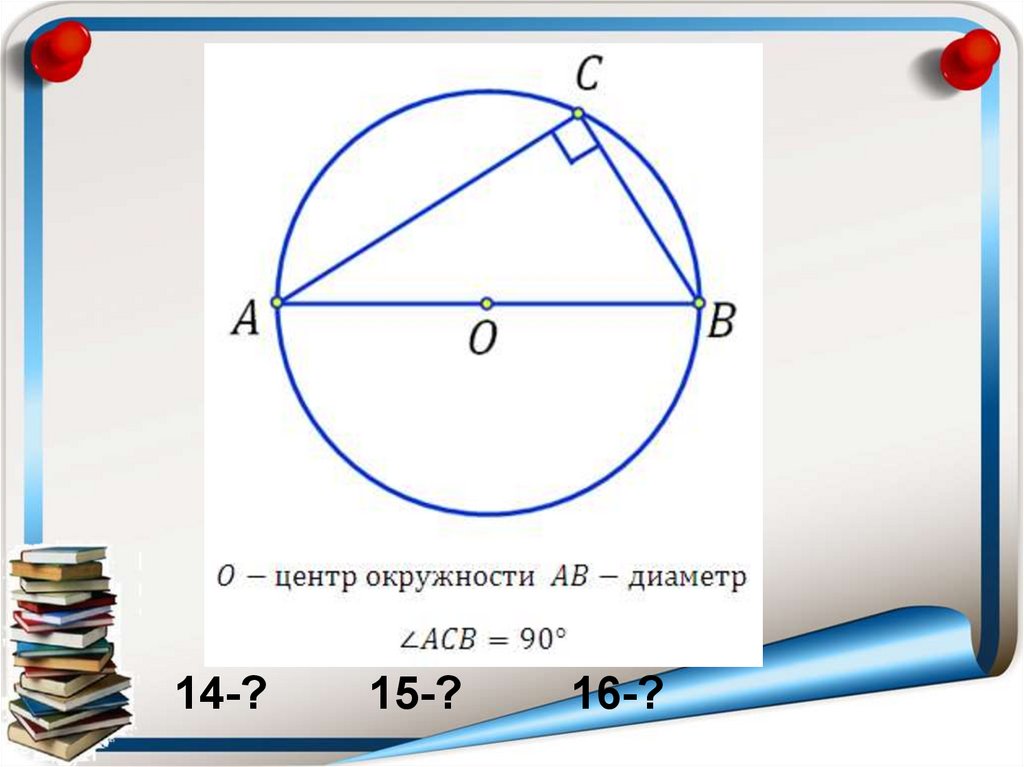
13.

14-?
15-?
16-?

14.

1. …меньше суммы двух его сторон.
2. … равны.
3. … равны.
4. … медианой и биссектрисой.
5. … равнобедренный.
6. … равнобедренный.
7. … прямоугольным.
8. … 90 градусов.
9. … сумме квадратов катетов.
10. …прямоугольный.
11. …половине произведения его катетов.
12. …половине гипотенузы.
13. …половине произведения высоты на его основание.
14. … прямой.
15. … на середине его гипотенузы.
16. … её диаметром.

15.

16.

17.

18.

19.

20.

1. Если AD=AC, то треугольник ACD равнобедренный,
2. значит < ADC = < ACD
3. (180 ⁰ - 10 ⁰) /2 = 170 ⁰ /2 = 85⁰.
4. < ДСВ=< АСВ - < ДСА=166-85=81⁰.
Ответ: < ДСВ = 81⁰.

21.

Рассмотрим прямоугольный треугольник ОКМ
ОМ=ОВ=13 см(ОМ и ОN - радиусы)
ОК=ОВ-КВ=13-1=12 см
По теореме Пифагора
ОМ²=OK²+MK²
13²=12²+MK²
MK²=169-144
MK²=25
MK=5
5. Т.к. МК=КN ( К-середина хорды), то
МN=МК+KN=5+5=10 см
Ответ: MN=10 см.
1.
2.
3.
4.

22.

Чтобы найти площадь треугольника с заданным
основанием, надо найти его высоту.
Из вершины треугольника опускаем на основание высоту.
Она же является и медианой: 60:2=30.
Рассмотрим прямоугольный треугольник у которого
гипотенуза с=34, а катет b=30.
Находим второй катет (он же высота) по теореме
Пифагора:
a² = c² - b², а = h.
h²= 34²- 30²= 256 Извлечём квадратный корень h =16.
S=1/2ah=1/2*16*60=480.
Ответ: 480.

23.

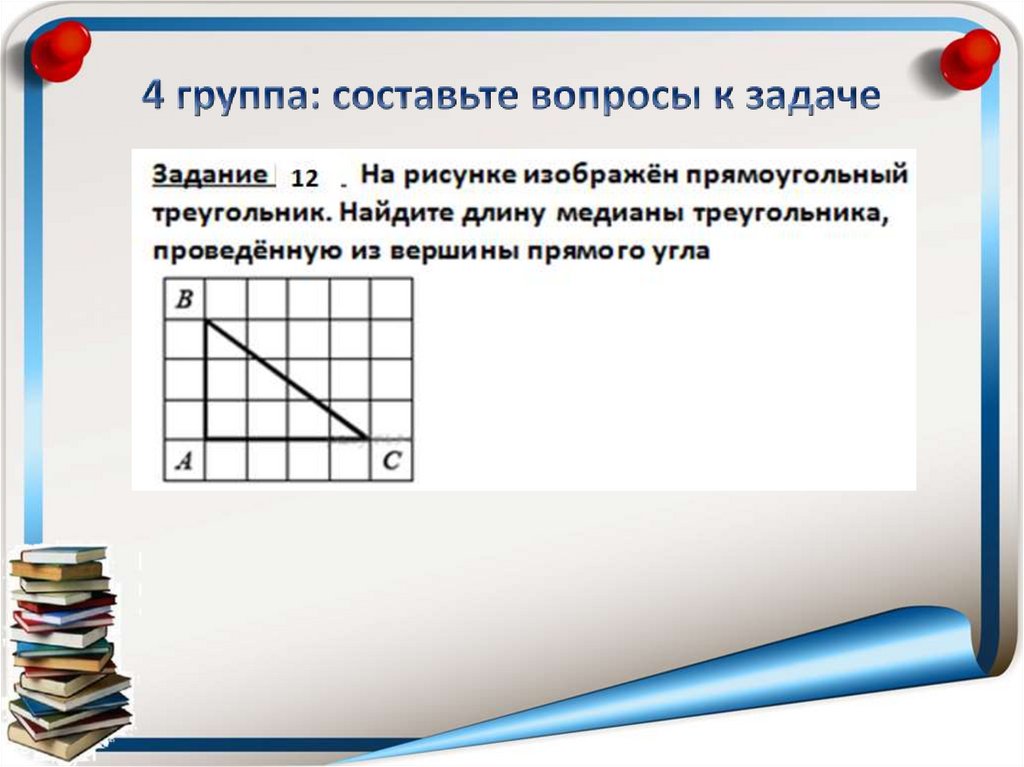
1. Медиана, проведённая из прямого угла равна половине
гипотенузы.
2. Гипотенуза равна √3²+4²=√25=5.
3. Медиана равна 5:2=2,5.
4. Ответ: 2,5.

24.

Задание 13: Выберите верные утверждения
1. Треугольник со сторонами 3, 4, 5 является тупоугольным.
2. Центр окружности, описанной около треугольника со
сторонами 3, 4, 5 находится на стороне этого треугольника.
3. Биссектриса равнобедренного треугольника, проведенная
из вершины, противолежащей основанию, делит его
основание на две равные части.
4. Площадь прямоугольного треугольника меньше
произведения его катетов.
5. Сумма углов любого треугольника равна
360 градусов.

25.

Составьте вопросы к задачам
Найдите ответы на поставленные
вопросы
Решите задачи