Similar presentations:
Взаимосвязи между двумя переменными и проверка гипотез
1.
Взаимосвязи между двумяпеременными и проверка
гипотез
2.
Гипотезы и типы переменных• Независимая переменная – Х
• Зависимая переменная – У
• Латентные переменные – скрыты переменные
• Независимые переменные – Х1 и Х2
• Гипотеза – научно-обоснованное предположение о наличии или
отсутствии (и силе) отношения между Х и У (Х1 и Х2).
3.
Гипотезы в статистике• Нулевая гипотеза (H0) — принимаемое по умолчанию предположение
о том, что не существует отношения между двумя переменными
(наблюдаемыми событиями, феноменами и пр.).
• Нулевая гипотеза верна пока нельзя доказать обратное.
• Альтернативная гипотеза (H1) – альтернативное предположение о
существовании отношений между переменными.
• H0 и H1 – формулируются исходя из программы исследования, с
опорой на теоретическую рамку, задачи и выделенные операнты! или
ключевые характеристики.
• H0 и H1 – частных гипотез, которые сформированы еще ДО
исследования и проверяются в процессе анализа по результатам.
4.
Гипотезы в статистике• Научный вывод, опирающийся на статистику, это тоже вероятностный
вывод.
• Он может быть ошибочным!
• Ошибка первого рода (α-ошибка, ложноположительное заключение)
— ситуация, когда отвергнута верная нулевая гипотеза (об отсутствии
связи между явлениями или искомого эффекта).
• Ошибка второго рода (β-ошибка, ложноотрицательное заключение) —
ситуация, когда принята неверная нулевая гипотеза.
• Важно: корреляция (и пр. стат. показатели) не означают каузацию –
причинно-следственную связь.
5.
Причина/следствие или связь/ассоциация• Одна переменная причина другой – необходимое и достаточное
условие:
• если есть А, всегда происходит B
• если нет А, никогда не происходит B
• Две переменные связаны между собой, часто происходят вместе
или изменяются:
• в одном направлении – когда А увеличивается, увеличивается B
• в противоположных направлениях – когда А увеличивается, B –
уменьшается
6.
Все со всем: мусор вводим, мусорполучаем
• размер обуви и скорость чтения; продажи мороженного и
количество изнасилований; % обнаженных частей тела и
количество купающихся
• рост и количество больничных; сексуальная активность и
склонность к депрессии
• успеваемость ребёнка связана с образованием родителей,
образование родителей связано с их доходом, а доход родителей
связан с их образованием…
• потребление электроники и продолжительность жизни
7.
Дополнительная проверка: признаки• Сила ассоциации (позволяет ли величина риска исключить другие факторы)
• Устойчивость (воспроизводимость результатов разными исследователями, в
разных условиях)
• Специфичность (влияние связано с конкретным эффектом, а не широким
спектром следствий)
• Необратимость (нет связи в обратном направлении)
• Временной порядок (причина раньше следствия)
• Правдоподобность (есть ли надёжные научные механизмы, объясняющие
ассоциацию)
• Экспериментальные данные (показывает ли физическое вмешательство
результаты согласованные с наблюдаемой ассоциацией)
• Аналогия (есть ли похожие результаты отношений между причиной и
следствием, на которых мы можем построить аналогию)
8.
Отступление: стат. значимость• Sig. [significance] показывает вероятность (p-value) того, что
наблюдаемое распределение случайно
• Если Sig. (p) > 0,05 – мы говорим о том, что наблюдаемая между
переменными взаимосвязь является результатом случайности. Мы не
можем утверждать, что она существует и в генеральной совокупности.
• Если Sig. (p) < 0,05, то мы на 95% уверенны, что обнаруженная связь
неслучайна, т.е. существует в генеральной совокупности (при условии
правильно сделанной выборки).
• Обратное значение p – α (достоверность результата, если р=0,05, то
α=0,95).
• Важная величина для оценки значимости любого показателя наличия
связи (НО не сама связь).
• Используется для перенесения на ген. совокупность.
9.
Отступление: стат. значимость• p < 0.01 – p меньше, чем 1 из 100:
• если в генеральной совокупности между X и У нет взаимосвязи, то
обнаруженная нами связь по чистой случайности появилась бы в 1
выборке из каждых 100
• p = 0.10 – p равно 10 из 100:
• наблюдаемая нами связь между Х и У случилась бы в десяти выборках из
100 даже если в генеральной совокупности связь между Х и У = 0
• p > 0.05 – p больше, чем 5 из 100:
• если в генеральной совокупности нет связи между Х и У, то наблюдаемые
нами результаты появились бы более, чем в 5 выборках из 100 по чистой
случайности
10.
Варианты сочетаний проверки гипотез• Проверки гипотез связаны с теми шкалами, которые
представляют ту или иную переменную/признак.
• Прежде чем проводить анализ – смотрим на шкалу.
• Три основные группы сочетаний:
• Категориальная-категориальная – непараметрические тесты
• Категориальная-метрическая
• Метрическая-метрическая – параметрические тесты
• Для подтипов могут использоваться собственные показаетли.
11.
Категориальная + категориальная• столбчатые диаграммы
• таблицы сопряженности, анализ условных распределений
• меры ассоциации: лямбда, гамма, фи
• экстраполяция: хи-квадрат
12.
Категориальная + метрическая• бокс-плоты
• сравнение средних значений
• мера ассоциации: эта
• экстраполяция: t test
13.
Метрическая + метрическая• точечная диаграмма
• мера ассоциации: корреляция
• экстраполяция: регрессия
В некоторых случаях упорядоченная порядковая и ранговая могут
рассматриваться через метрические показатели (интервальность).
14.
Категориальные+
категориальные
15.
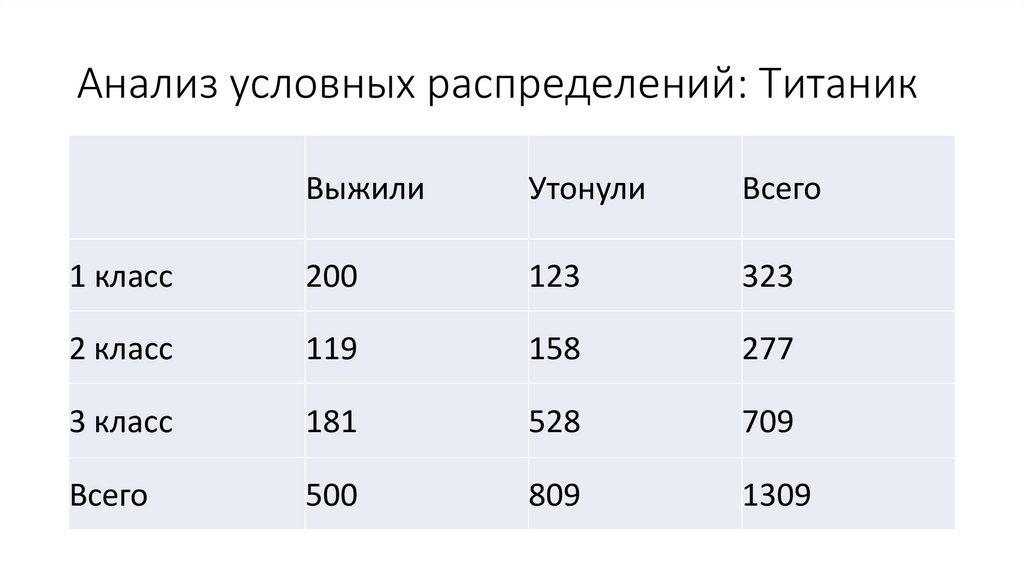
Анализ условных распределений: ТитаникВыжили
Утонули
Всего
1 класс
200
123
323
2 класс
119
158
277
3 класс
181
528
709
Всего
500
809
1309
16.
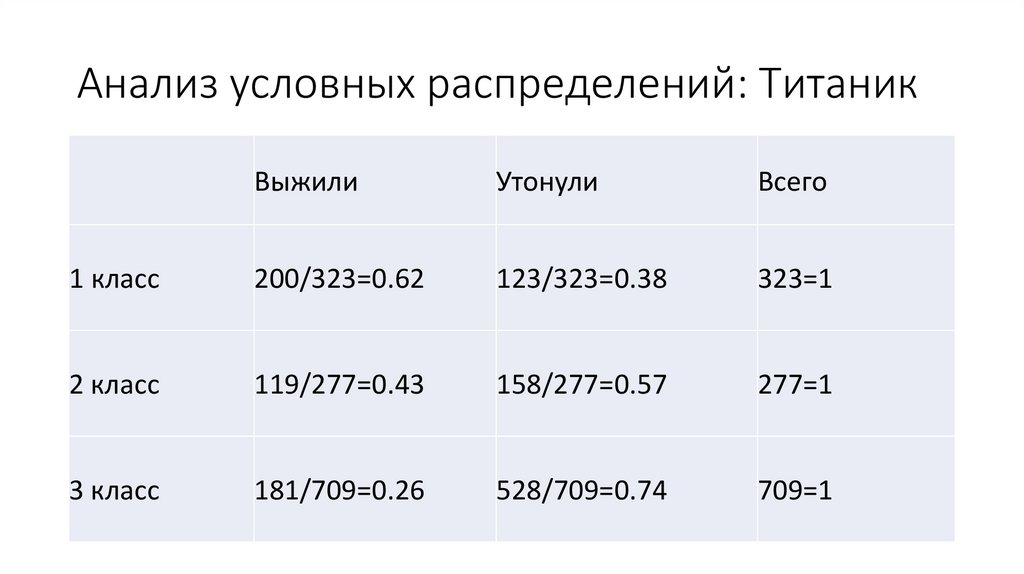
Анализ условных распределений: ТитаникВыжили
Утонули
Всего
1 класс
200/323=0.62
123/323=0.38
323=1
2 класс
119/277=0.43
158/277=0.57
277=1
3 класс
181/709=0.26
528/709=0.74
709=1
17.
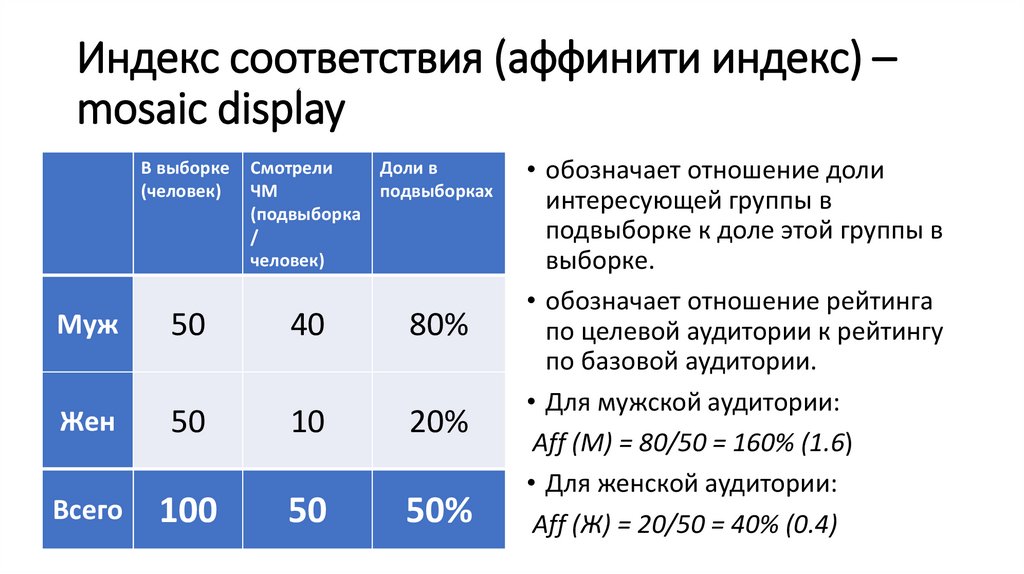
Индекс соответствия (аффинити индекс) –mosaic display
В выборке
(человек)
Смотрели
Доли в
ЧМ
подвыборках
(подвыборка
/
человек)
Муж
50
40
80%
Жен
50
10
20%
Всего
100
50
50%
• обозначает отношение доли
интересующей группы в
подвыборке к доле этой группы в
выборке.
• обозначает отношение рейтинга
по целевой аудитории к рейтингу
по базовой аудитории.
• Для мужской аудитории:
Aff (M) = 80/50 = 160% (1.6)
• Для женской аудитории:
Aff (Ж) = 20/50 = 40% (0.4)
18.
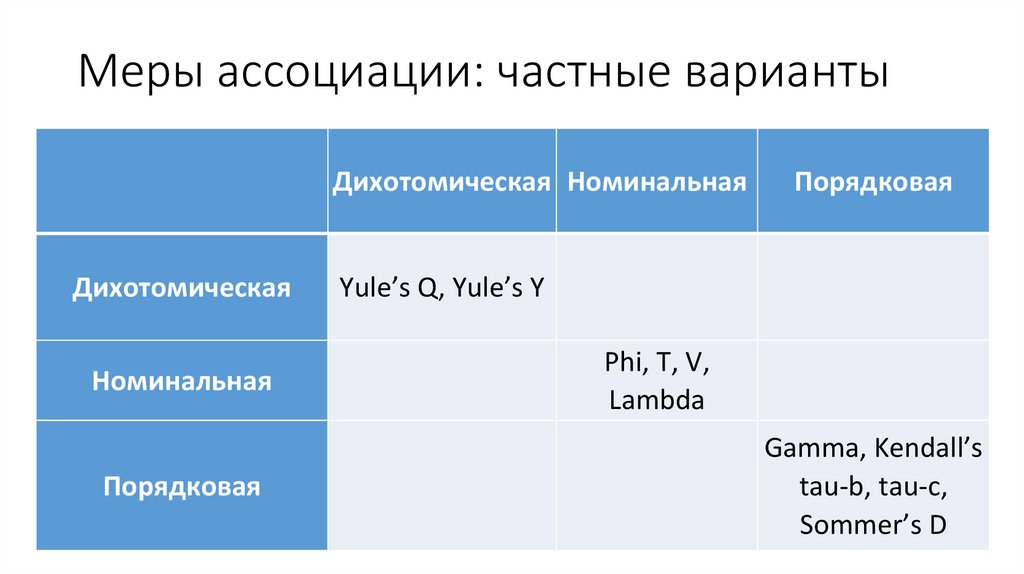
Меры ассоциации: частные вариантыДихотомическая Номинальная
Дихотомическая
Номинальная
Порядковая
Порядковая
Yule’s Q, Yule’s Y
Phi, T, V,
Lambda
Gamma, Kendall’s
tau-b, tau-c,
Sommer’s D
19.
Силы связейИнтерпретация значений PRE коэффициентов:
• ниже 0,1 – слабая связь
• от 0,1 до 0,2 – умеренная связь
• от 0,2 до 0,3 – умеренно сильная связь
• 0,3 и выше – сильная связь
• 0 – нет связи, признаки независимы
• 1 – идеальная связь (иногда -/+ - прямая и обратная)
20.
Фи [Cramer’s phi]• Cramer's phi = 0.37 – корреляция, симметричная
• φ2 (phi*phi = 0.137) – PRE (коэффициент детерминации)
Сандалии Кроссовки
Юноши 6
Девушки 13
Всего
19
17
5
22
Кожаные
ботинки
13
7
20
Ботинки Другое
Всего
9
16
25
50
50
100
5
9
14
Cramer's phi = 0.37 (φ2 = 0.137) означает, что предпочтения обуви
студентов на 14% определяются их полом. А значит, 86% разброса
предпочтений остается без объяснения, есть и другие переменные,
которые на это влияют.
21.
Лямбда [Lambda]Спорт
Сериалы
Мужчины
Женщины
900
100
300
700
Всего зависимая
переменная
1200
800
• = 0,5
• Значение лямбды говорит о сильной положительной ассоциации между
полом индивида и его предпочтением ТВ программ. Мужчины скорее
смотрят спорт, а женщины чаще предпочитают сериалы.
• Значение лямбды показывает, что нам удалось уменьшить ошибочность
нашего предсказания на 50%, когда мы опирались на пол индивида, чтобы
предсказать его ТВ предпочтения.
22.
Экстраполяция: хи-квадрат• НЕ мера ассоциации!
• Это не дескриптивная, а инференциальная статистика, то есть
используется не для оценки связи между Х и У, а для проверки
можно ли распространять обнаруженную в выборке
зависимость на генеральную совокупность.
• Разница между ожидаемыми значениями и реальными.
• Имеет разные значения, но всегда ПОЛОЖИТЕЛЬНЫЕ!
23.
Экстраполяция: хи-квадратДля оценки необходимо:
• Значение хи-квадрат
• df = (r – 1)*(c – 1) = (число рядов – 1) *(число столбцов – 1)
• Стат. значимость
• Показывает насколько должна отклонятся величина в каждой
«ячейки», чтобы это отклонение было статистически значимым.
Или можно было говорить о наличии различий, которые
сохраняются в генеральной совокупности.
• Чем больше хи-квадрат, тем больше различия в подвыборках.



















 mathematics
mathematics








