Касательная к окружности. Урок по геометрии в 8 классе

1.

Ни 30 лет, ни 30 столетий не оказывают никакого
влияния на ясность или на красоту геометрических
истин.
Кэрролл Л.
L
О
Урок по геометрии в 8 классе
а

2.

Верите ли вы…
• что самая простая из кривых линий – окружность?
• что древние индейцы считали самым важным элементом
окружности радиус?
• что впервые термин «радиус» встречается лишь в 16 веке?
• что в переводе с латинского радиус означает «луч»?
• что при заданном периметре именно окружность ограничивает
наибольшую площадь?
• что в русском языке слово «круглый» означает высшую
степень чего-либо?
• что выражение «ходить по кругу» когда-то означало
«прогресс»?
• что хорда в переводе с греческого означает «струна»?
• что определение «касательной» уже есть в первом учебнике
геометрии – «Начала» Евклида?

3.

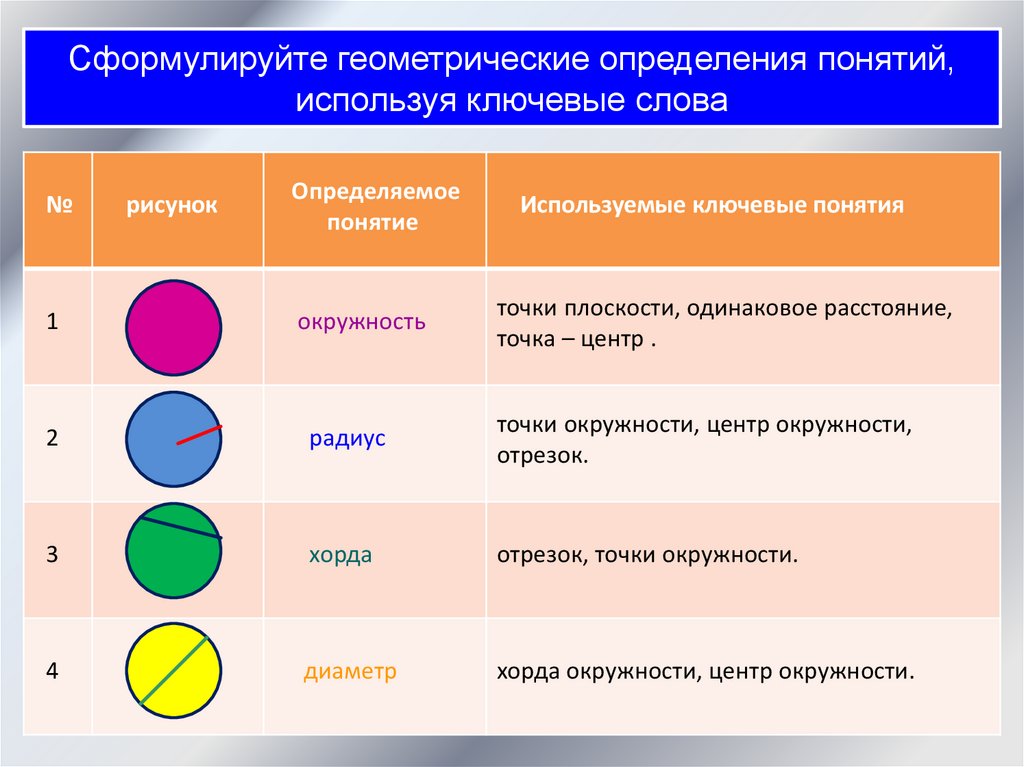
Сформулируйте геометрические определения понятий,
используя ключевые слова
№
1
рисунок
Определяемое
понятие
окружность
Используемые ключевые понятия
точки плоскости, одинаковое расстояние,
точка – центр .
2
радиус
точки окружности, центр окружности,
отрезок.
3
хорда
отрезок, точки окружности.
4
диаметр
хорда окружности, центр окружности.

4.

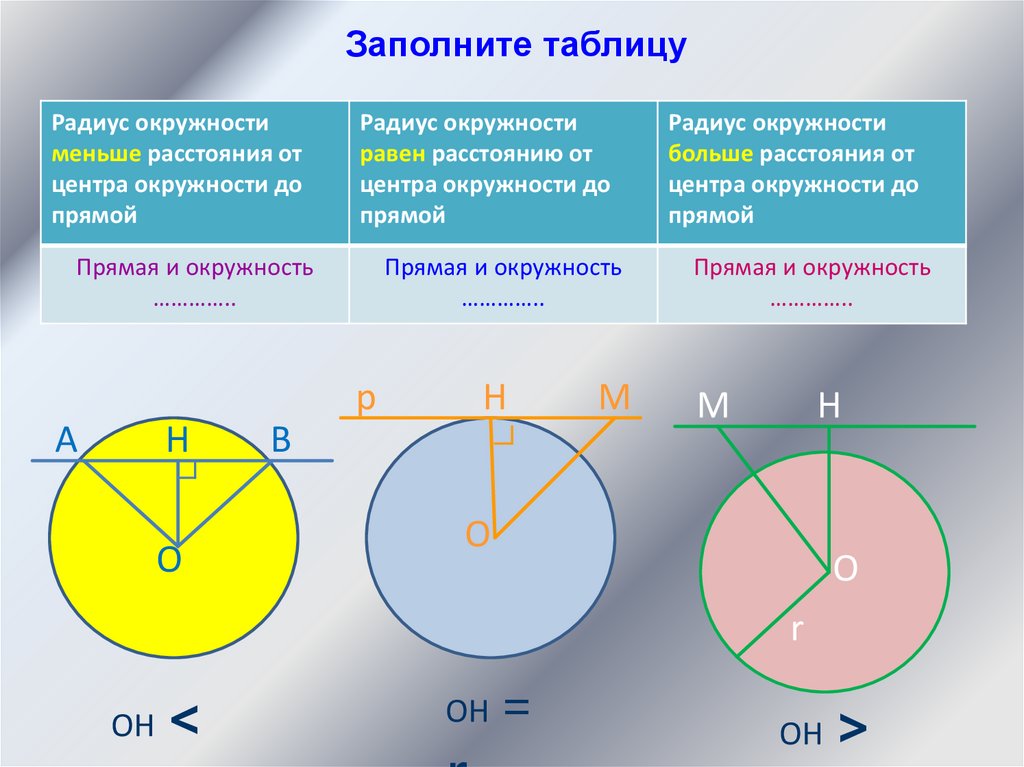
Заполните таблицу
Радиус окружности
меньше расстояния от
центра окружности до
прямой
Радиус окружности
равен расстоянию от
центра окружности до
прямой
Прямая и окружность
…………..
Прямая и окружность
…………..
р
А
Н
О
Н
В
М
Радиус окружности
больше расстояния от
центра окружности до
прямой
Прямая и окружность
…………..
М
Н
О
О
r
ОН
<
ОН =
ОН
>

5.

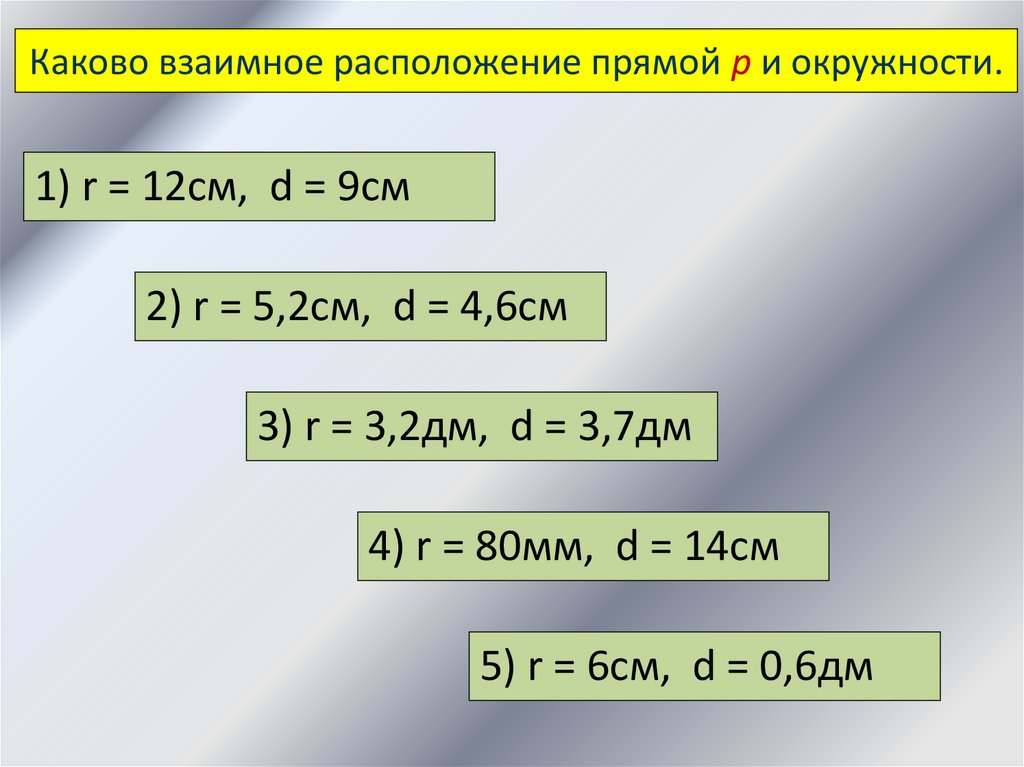
Каково взаимное расположение прямой р и окружности.
1) r = 12см, d = 9см
2) r = 5,2см, d = 4,6см
3) r = 3,2дм, d = 3,7дм
4) r = 80мм, d = 14см
5) r = 6см, d = 0,6дм

6.

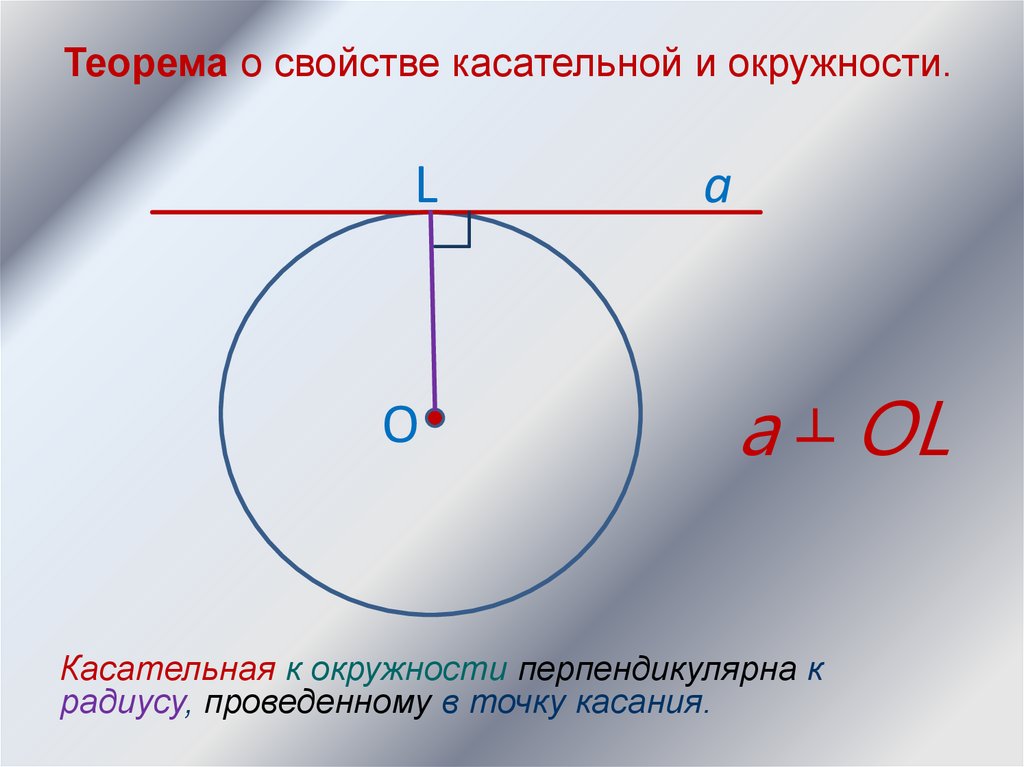
Теорема о свойстве касательной и окружности.
L
О
а
a ┴ OL
Касательная к окружности перпендикулярна к
радиусу, проведенному в точку касания.

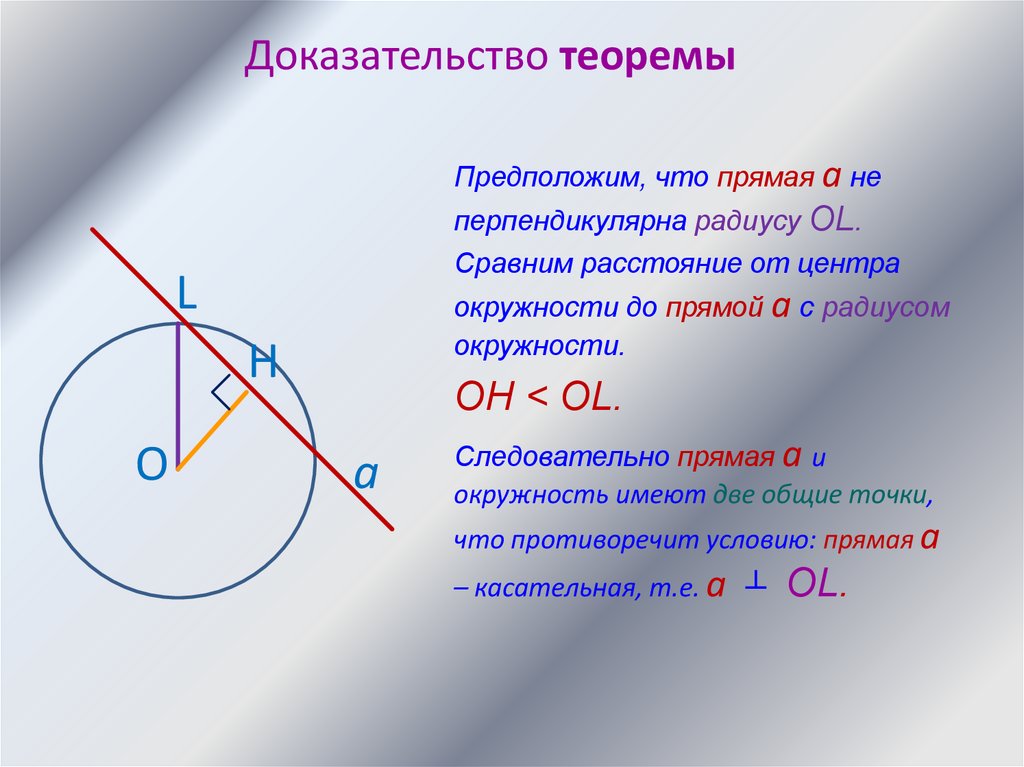
7.

Доказательство теоремы
Предположим, что прямая а не
перпендикулярна радиусу ОL.
Сравним расстояние от центра
L
окружности до прямой а с радиусом
окружности.
Н
О
OH < OL.
а
Следовательно прямая а и
окружность имеют две общие точки,
что противоречит условию: прямая а
– касательная, т.е. а ┴
OL.

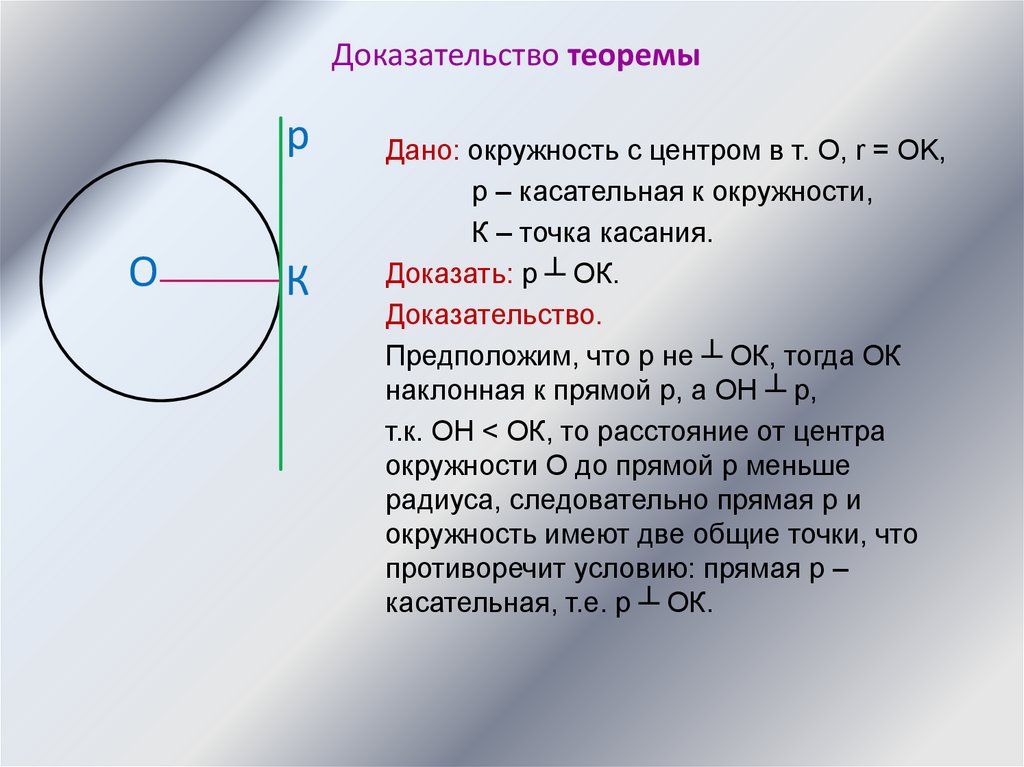
8.

Доказательство теоремы
р
О
К
Дано: окружность с центром в т. О, r = OK,
p – касательная к окружности,
К – точка касания.
Доказать: p ┴ ОК.
Доказательство.
Предположим, что р не ┴ ОК, тогда ОК
наклонная к прямой р, а ОН ┴ р,
т.к. ОН < ОК, то расстояние от центра
окружности О до прямой р меньше
радиуса, следовательно прямая р и
окружность имеют две общие точки, что
противоречит условию: прямая р –
касательная, т.е. р ┴ ОК.

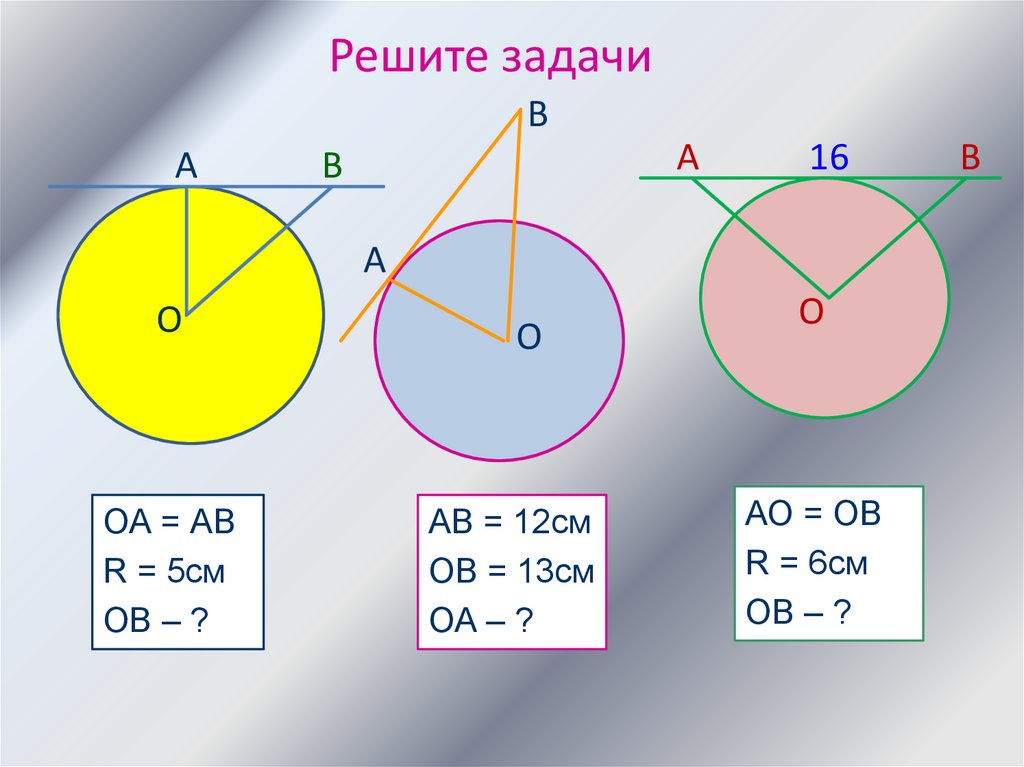
9.

Решите задачи
В
А
А
В
16
А
О
ОА = АВ
R = 5см
ОВ – ?
О
АВ = 12см
ОВ = 13см
ОА – ?
О
АО = ОВ
R = 6см
ОВ – ?
В

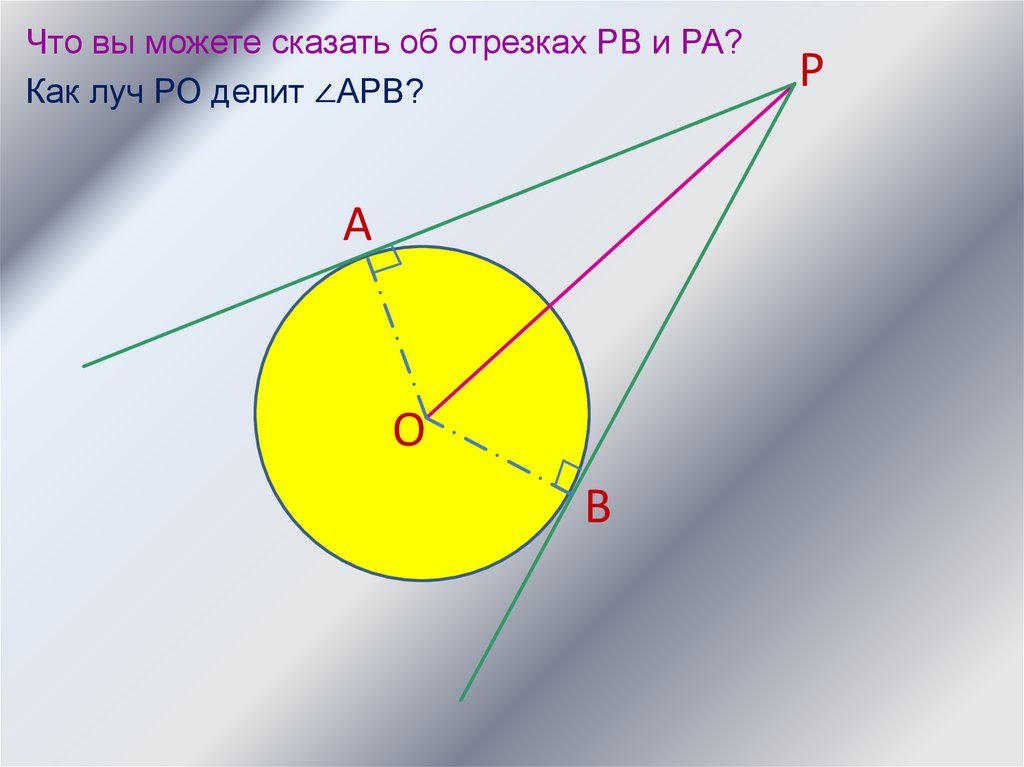
10.

Что вы можете сказать об отрезках РВ и РА?
Как луч РО делит ∠АРВ?
А
О
В
Р

11.

Решение задач
P
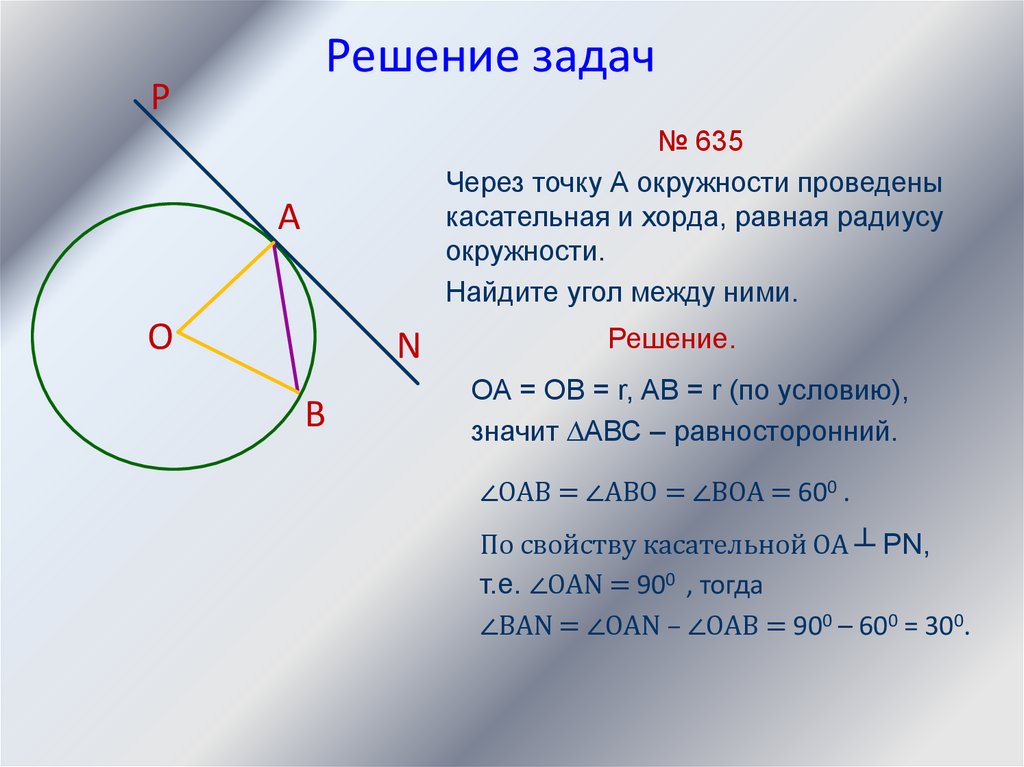
№ 635
Через точку А окружности проведены
касательная и хорда, равная радиусу
окружности.
Найдите угол между ними.
А
О
N
В
Решение.
ОА = ОВ = r, АВ = r (по условию),
значит ∆АВС – равносторонний.
∠ОАВ = ∠АВО = ∠ВОА = 600 .
По свойству касательной ОА ┴ РN,
т.е. ∠ОАN = 900 , тогда
∠ВАN = ∠ОАN – ∠ОАВ = 900 – 600 = 300.

12.

Решение задач
А
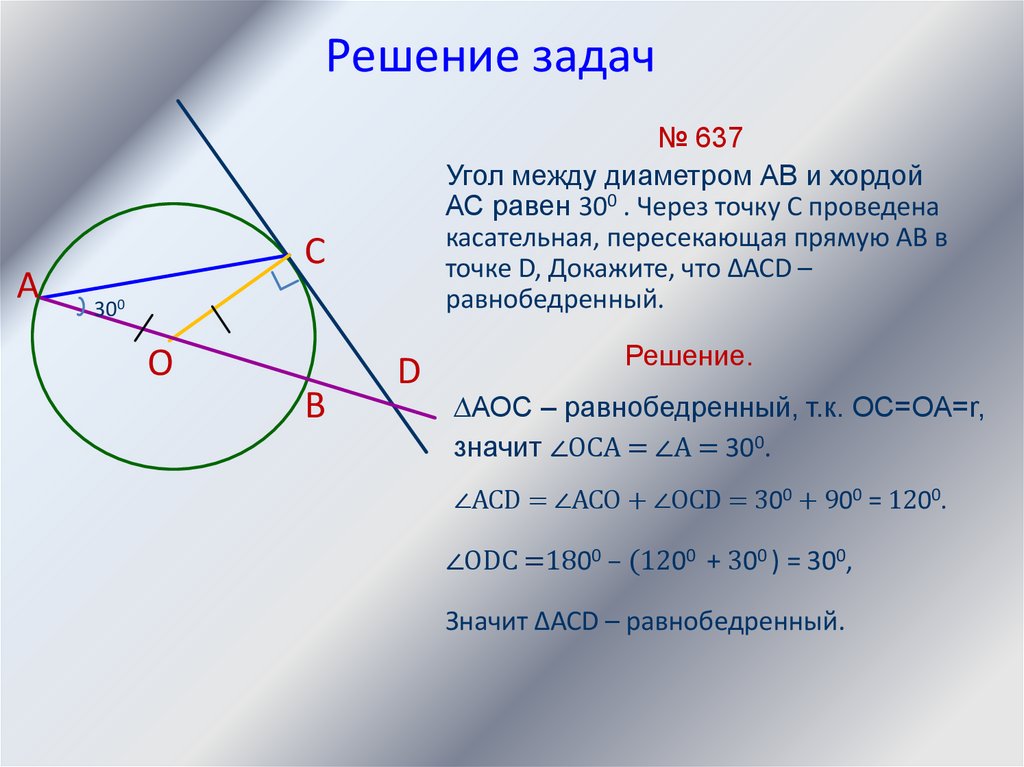
№ 637
Угол между диаметром АВ и хордой
АС равен 300 . Через точку С проведена
касательная, пересекающая прямую АВ в
точке D, Докажите, что ∆АСD –
равнобедренный.
С
300
О
В
D
Решение.
∆АОС – равнобедренный, т.к. ОС=ОА=r,
значит ∠ОСА = ∠А = 300.
∠АСD = ∠АСO + ∠OСD = 300 + 900 = 1200.
∠ОDC =1800 – (1200 + 300 ) = 300,
Значит ∆АСD – равнобедренный.

13.

Решение задач
А
2
О
В
№ 638
Прямая АВ касается окружности с
центром О радиуса r в точке В.
Найдите АВ, если ОА = 2см, а r = 1,5см.
Решение.
По свойству касательной АВ ┴ ОВ,
следовательно ∆ОВА - прямоугольный.

14.

Решение задач
А
В
600
О
№ 639
Прямая АВ касается окружности с центром
О радиуса r в точке В.
Найдите АВ, если ∠АОВ = 600, а r = 12см.
Решение.
По свойству касательной АВ ┴ ОВ,
следовательно ∆ОВА - прямоугольный.
∠ОАВ = 900 – 600 = 300 , тогда ОА = ОВ * 2 = 12 * 2 = 24 (см).

15.

Рефлексия
• Каким свойством обладает касательная к
окружности?
• Сформулируйте теорему о двух касательных к
окружности, проведенных из одной точки, лежащей
вне этой окружности.
• Возникали ли у вас трудности с усвоением
сегодняшнего материала? И по какой причине?

16.

На дом:
• П. 69;
• № 633, № 636.