Показательная функция, её график и свойства

1. Муниципальное автономное учреждение дополнительного образования «Центр детского творчества»

Показательная функция, её график
и свойства
Машакова Кызтаман Баубековна

2. Организационный момент. «Всё в наших руках»

Притча
Жил мудрец, который знал все. Один человек захотел
доказать, что мудрец знает не все. Зажав в ладонях бабочку, он
спросил: «Скажи, мудрец, какая бабочка у меня в руках: мертвая
или живая?» А сам думает: «Скажет живая, я ее омертвлю,
скажет мертвая – выпущу». Мудрец, подумав, ответил: «Все в
твоих руках».
Наша же главная задача – включить всего себя в деятельность,
обеспечивающую формирование и развитие познавательных
способностей, ключевых компетенций, необходимых для
успешности в учебе и жизни. Задача эта будет выполнима в
случае, если усилия всех нас будут направлены в единое русло и
из успехов каждого сложится общий успех.

3. Актуализация знаний

Найти формулу, соответствующую каждому графику. Результат
записать в таблицу.(устная работа 5 минут).
1
2
3
4
5
10
7
9
16
4
8
7
14
3
6
2
4
10
3
8
1
0
0
-6
-5
-4
-3
-2
-1
-1 0
1
2
3
4
5
6
-5
-4
-3
-2
4
-1-2
-1
-1
0
1
2
3
4
1
5
-6 -5 -4 -3 -2 -1-1 0
-2
-4
-5
-3
-6
0
-3
-2
-3
2
-5
3
1
2
6
-7
5
5
12
-7
1
3
5
7
-9
1)у = 2х+5; 2)у = cos(x+3); 3)3х + у = 4;
1
-5
-5
-10
График
-3
-4
-8
2
4)у=1\х; 5) у = x+3; 6)у = х3
3
7) у = х2
4
Формула
Какие из данных функций являются монотонными?
Какие из данных функций определены на всей числовой прямой?
Какие из данных функций имеют наименьшее или наибольшее значение?
1
2
3
4
5
6

4. Изучение нового материала

Всегда ли выполнимо действие возведение в степень на множестве
действительных чисел?
Разбор построения неизвестного графика
у ах
Какие значения может принимать а ?
Проверка вариантов значений(использование определения степени с
рациональным показателем).
При а=0 – линейная функция у=0
При а=1 – линейная функция у=1
При а>1 – ?
При а 1 – ?
Построить график функций на шаблонах координатных плоскостей
у 2х
1
у
2
х
у 3х
у 5х

5. Построение графика функции

у 2
у
12
11
10
9
8
7
у=2х
6
5
4
3
2
1
0
-4
-3
-2
-1
0
1
2
3
4
х
х
у
-2
0,25
-1
0,5
0
1
1
2
2
4
3
8
х

6. Построение графика функции

1
у
2
у
12
11
10
9
1
у
2
х
8
7
6
5
4
3
2
1
0
-4
-3
-2
-1
0
1
2
3
х
4
х
у
-3
8
-2
4
-1
2
0
1
1
0,5
2
0,25
х

7. Графики функции

у а
х
а>1
у
12
11
10
9
у 2х
8
7
6
5
у 3х
4
3
2
у 5х
1
0
-4
-3
-2
-1
0
1
2
3
4
x

8. Графики функции

у а
х
0<а<1
у
12
11
10
9
8
7
6
1
у
5
х
1
у
3
х
5
4
3
2
1
у
2
1
0
-4
-3
-2
-1
0
1
2
3
4
x
х

9. Назначение иллюстраций Анализ построенных графиков по готовым чертежам: Вывод: зависимость вида у=ах при определённых условиях

10. Изучение свойств показательной функции с использованием уже построенных графиков

12
12
11
11
10
10
1
у
2
9
у 2
х
8
7
6
5
9
х
8
7
6
5
4
4
3
3
2
2
1
1
0
0
-4
-3
-2
-1
0
1
2
3
-4
4
у 3
11
10
у 5
9
х
х
1
у
3
0
1
2
3
4
9
7
6
6
5
5
у 2
х
4
3
1
у
2
1
0
0
1
2
3
4
х
10
7
2
-1
-1
1
у
5
11
8
3
-2
х
8
4
-3
-2
12
12
-4
-3
-4
-3
-2
х
2
1
0
-1
0
1
2
3
4

11. Свойства показательной функции

у а
а>1
0<а<1
Область
определения
функции
(- ∞;+∞)
(- ∞;+∞)
Множество
значений
функции
(0;+∞)
Свойства
функции
Возрастание,
убывание
(0;+∞)
возрастает убывает
График функции проходит через точку с координатами (0;1).
х

12. Почему так важно знать свойства показательной функции?.

Да , великие математики действительно влюблены в «царицу наук»,
и согласно песне «превращают свою жизнь в цветы».
По закону показательной функции размножалось бы все живое на Земле, если бы
для этого имелись благоприятные условия, т.е. не было естественных врагов и
было вдоволь пищи. Доказательство тому – распространение в Австралии
кроликов, которых там не было раньше. Достаточно было выпустить пару
особей, как через некоторое время их потомство стало национальным бедствием.
В природе, технике и экономике встречаются многочисленные процессы, в ходе
которых значение величины меняется в одно и то же число раз, т.е. по закону
показательной функции. Эти процессы называются процессами органического
роста или органического затухания.
Например, рост бактерий в идеальных условиях соответствует процессу
органического роста; радиоактивный распад веществ – процессу органического
затухания.
Законам органического роста подчиняется рост вклада в Сберегательном банке,
восстановление гемоглобина в крови у донора или раненого, потерявшего много
крови.

13. Схематичное изображение графика функции у=ах

а>1
0<а<1
у ах

14. Построение графика функции путем сдвига вдоль оси ординат

у= ах-с - параллельный перенос графика функции у=ах на с единиц вправо,
Построение
графика
если
ус>0, и на ∣ с ∣ единиц влево, если с<0.
у
14
12
13
11
12
10
9
11
8
10
7
9
у 2х
6
8
у 2х 2
5
7
4
6
3
5
2
4
1
3
0
у 2
2
1
х
-3
-2
-1
0
1
2
-3
-2
-1
0
-1
-2
0
-4
-4
3
х
4
-3
1
2
3
у 2х 2
4
х

15. Построение графика функции путем сдвига вдоль оси абсцисс:

ах-с
у=
- параллельный перенос графика функции
с>0, и на ∣ с ∣ уединиц влево, если с<0
у 2если
на с единиц вправо,
у
12
11
11
10
10
9
9
8
8
у 2х
7
6
6
5
5
у 2
4
3
2
у 2
1
0
-2
х 2
12
7
-4
у=ах
0
2
4
х 2
4
3
2
х 2
у 2х
1
х
0
6
-5
-4
-3
-2
-1
0
1
2
3
4
х

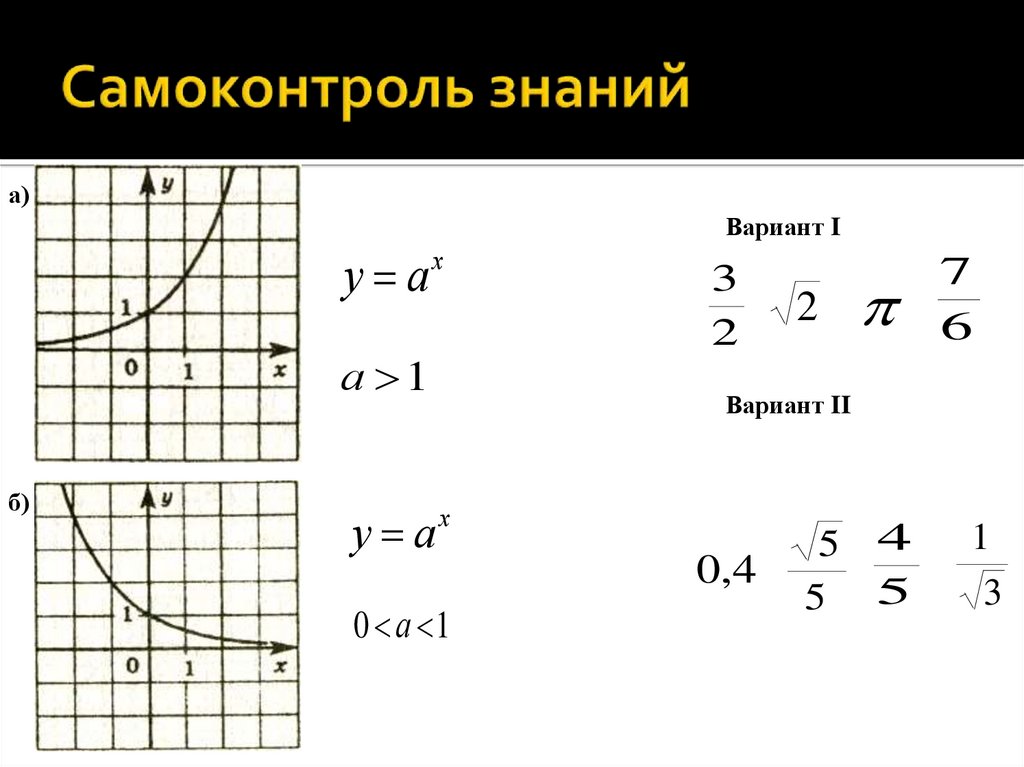
16. Самоконтроль знаний

а)
у а
х
Выберите из предложенных оснований
те, которые подойдут для построения
графика:
Вариант I а)
а 1
б)
у а
Вариант II б)
0,4
2
4
5
5
0,3
5
х
0 а 1
1
3
3
2
2
7
6

17. Самоконтроль знаний

а)
Вариант I
у а
х
а 1
б)
у а
3
2
2
7
6
Вариант II
х
0 а 1
0,4
5 4
5 5
1
3

18. Алгоритм построения графика функции:

1.у = 3x (пунктиром ось Ох)
1. у = 3 x (пунктиром ось Ох и ось Оу)
2.у=3x + 2 (переносим ось Ох на 2 единицы вниз) 2. у=3x-2 (переносим ось Оу на 2 единицы влево)
3. у=3x-2 – 2 (переносим ось Ох на 2 единицы вверх)

19. Алгоритм построения графика у=|3x-2 - 2|

1. у = 3x (пунктиром ось Ох и ось Оу)
2. у=3x-2 (переносим ось Оу на 2 единицы влево)
3. у=3x-2 – 2 (переносим ось Ох на 2 единицу вверх)
4. у=|3x-2 - 2| (та часть графика, которая находится ниже оси Ох, зеркально отображается вверх)

20. Исследовательская работа в группах «Терпение и труд всё перетрут!»

1 группа
2 группа
I. Дать определение области значения функции.
II. Назвать область значения функций:
а) у = 3x,
а) у = 3 x,
б) у = -3 x,
б) у = -3 x,
в) у = (1/5) x,
в) у = (1/5) x,
г) у = (-1/4) x
г) у = (-1/4)
д) у = 3 x – 2.
д) у = 3 x – 2.
III. Дана функция: у = а x ± b. Вывести правило, по которому можно, не выполняя
построение графика данной функции, найти область значения функции.
Построить графики функций и сделать вывод: Как найти О.З. функции
у = а x + b?
у = а x - b.
a) у = 3 x,
a) у = 3 x,
б) у = 3 x + 6,
б) у = 3 x - 6,
в) у = 3 x + 2,
в) у = 3 x - 2,
Изменится ли область определения данных функций?

21. Вывод:

Если у = а x + b,
то Е (у) = (b; +∞ ), Д (у) = (- ∞;+∞)
Если у = а x - b,
то Е (у) = (-b; +∞ ), Д (у) = (- ∞;+∞; )

22. Закрепление темы:

Какое из следующих чисел входит в
множество значений функции: у = 2 x + 4,
у = 2 x - 4, у = 2 x + 5, у = 2 x + 3,
1) 5; 2) 2; 3) 3; 4) 4

23. Решение:

Так как Е (у)= (4; +∞ ), то верный ответ :
5;
Так как Е (у) = (-4; +∞ ), то верный ответ:
2; 3; 4; 5;
Так как Е (у)= (5; +∞ ), то верный ответ :
ни одно из этих чисел
Так как Е (у)= (3; +∞ ), то верный ответ :
4; 5;