Similar presentations:
Тестирование
1.
Тестирование2.
Одним из этапов технологии программирования являетсятестирование программы.
ОПРЕДЕЛЕНИЕ:
Тестирование - процесс подготовки тестов и выполнения
программы для этих тестов с целью доказательства факта
наличия в программе ошибки.
Ошибка программы - наличие в программе “дефекта”, который
проявляется в том, что программа не может быть выполнена или
результаты работы программы отличаются от ожидаемых.
Ошибки бывают трех видов:
а) синтаксические ошибки;
б) логические ошибки;
в) алгоритмические ошибки.
3.
Синтаксические ошибки - это результат незнания языкапрограммирования или невнимательность программиста.
Проявляются эти ошибки в том, что программист не правильно
записывает ту или иную конструкцию языка программирования.
Пример:
1)
VAR
x: real;
...
for x:=1 to 10*10*10 do
x:= x +2;
переменная x не может быть параметром цикла, т. к. она не
ординального типа и ее значение изменяется в теле цикла.
4.
2)VAR
x: boolean;
...
case x off {1}
1: x:= 2;
2: x:=do; {2}
{5} 3: x:=if; {3}
конец {4}
ошибки:
1) вместо of употреблено off;
2) и 3) do и if зарезервированные слова, использовать которые нельзя в иных целях ,
кроме как элементы в соответствующих операторах : while, for, if ... then ... else;
4) использовано русское слово вместо end;
5) значения 1,2 и 3 не принадлежат типу boolean.
Как правило, синтаксические ошибки обнаруживаются на этапе трансляции
программы.
5.
Логические ошибки - это результат грубого просмотра, непониманияалгоритма программы, иногда непонимание смысла некоторых
конструкций языка программирования. Логические ошибки - это
ошибки в логике программы, но обусловленные внешними по
отношению к алгоритму факторами, т. е. алгоритм решения задачи
правильный, а программа составлена неправильно.
Пример:
задача: если x>0 то x:= x-y
иначе x:= y -x;
решение:
VAR
x,y: real;
...
if x<=y {1}
then x:=x/y {2}
else y:=y -x; {3}
1) грубый просмотр вместо x>0 использовано x =y:
2) описка вместо x-y записано x/y;
3) невнимательность вместо x:=y -x употреблено y:=y -x.
6.
Пример:задача:
Если x>y или y>x, то
если x- y 0, то x:=x - y иначе x:=y;
решение:
if(x>y) or (y>x) then
if x - y <> 0 then x:= x-y
else x:= y;
т. к. x>y или y>x, следовательно, y x и следовательно y -x
0 и тогда правильное решение:
if (x> y) or (y>x) then x:= x - y
else x:=y;
7.
Это пример двуликой ошибки:а) считая, что нет алгоритмической ошибки и т. к.
очевидно противоречие, программист не понял, что перед
ним задача:
если x>y и y>x то x:=x - y, иначе x:=y;
б) если считать приведенный пример некорректным, то
это образец алгоритмической ошибки, когда ошибка
алгоритма перешла в ошибку программы.
Таким образом, четкую грань между множествами
логических и алгоритмических ошибок провести нельзя.
Есть ошибки , которые легко отнести к логическим, и есть
ошибки, которые легко отнести к алгоритмическим.
8.
Пример:задача:
max(x,y) = x если x>y
y если y x
решение:
if x>y then max:= y
else max:= x;
ошибка - все сделано наоборот.
Есть ошибки, которые то ли логические, то ли алгоритмические.
Единственное, что объединяет логические и алгоритмические ошибки,
это то , что они проявляются только и только на этапе выполнения. А
следовательно, найти логические и алгоритмические ошибки , в отличие
от синтаксических, можно только на этапе выполнения программы.
9.
Желательно, чтобы они не проявлялись при промышленной эксплуатациипрограммы, на крайний случай при опытной эксплуатации.
Проявление ошибки не означает, что ошибка найдена. Процесс обнаружения
места и характера ошибки называют отладкой программы. Тогда как
тестирование программы - это процесс проявления, выявления наличия
ошибки в программе.
Таким образом , доказательство наличия ошибки в программе называют
тестированием программы.
Суть тестирования в следующем.
Известна формальная (неформальная) постановка задачи. Выбирается
один набор исходных данных. Для него определяют результат либо по
формальной постановке, либо по теоретически правильной программе (что
сделать иногда невозможно).
10.
Известна формальная (неформальная) постановка задачи. Выбираетсяодин набор исходных данных. Для него определяют результат либо по
формальной постановке, либо по теоретически правильной программе
(что сделать иногда невозможно).
Таким образом:
если х - исходные данные,
y - результат,
F - “формула” расчета,
то для правильной программы : y =F(x), x области допустимых
значений, и для неправильной программы y’= ~F(x) x области
допустимых значений и при этом y y'.
Если при заданном наборе получают результат отличный от ожидаемого,
то налицо наличие ошибки.
11.
Пару <x,y> - исходные данные и результаты называют тестом программы.Ели y = ~ F(x), то тест <x,y> ошибки в программе ~ F не обнаруживает.
Если y' = ~ F(x) F(x), то тест <x,y> ошибку в программе обнаруживает.
Последний тест называется удачным, а первый неудачным.
Пример:
задача:
max(x,y) = if x>y then x else y;
решение:
if x>y then max:=y
else max:= x;
тест 1: <(3,3),3> ошибку не находит т. к. при x=3 , y =3 то max =3;
тест 2: <(2,0),2> при x=2, y=0 получаем по решению max = 0, а это ошибка в
программе;
тест 3 : <(1,4),4> при x=1, y=4 получаем по решению max = 1 - ошибка в
программе.
12.
Методы тестированияВ зависимости от способа вычисления результата по исходным
данным все методы тестирования делятся на два класса: методы
“ черного ящика” и методы “ белого ящика”. Роль ящика
выполняет программа.
Методы “черного ящика” предполагают, что разработка тестов
осуществляется без использования знаний о структуре
программы, без привлечения сведений о логике программы.
Методы же “белого ящика” основаны на знаниях структуры и
логики программы.
Таким образом , разрабатывая тесты по методам “ черного
ящика” мы исходим из того, что нам не известна программа, но
известна постановка задачи.
13.
Xпрограмма
Y
14.
На основе этой постановки и определяется результат y=F(x) для теста <x,y>. Таким образом, мы знаем , что
подается на вход программы ~F(x) , что получается в
результате y=F(x) и, если
F(x) ~F(x), то программа
~F(x) содержит ошибку , иначе ошибка не найдена.
Разрабатывая тесты методами “белого ящика”, мы исходим
из того, что текст программы нам известен. Используя этот
текст, по исходным данным Х получают результат Y, но не с
использованием ЭВМ, а вручную.
Пусть y=F(x) - в ручную, а y' = ~F(x) - на ЭВМ и, если
есть отклонение y' y, то программа ~F содержит ошибку.
15.
Методы тестирования по “черному ящику”Конечная цель тестирования - доказать наличие ошибки в
программе. Доказать отсутствие ошибки в программе методами
тестирования практически не возможно по двум основным
причинам.
Во-первых, доказать, что та или иная программа не содержит
ошибку, используя тестирование, значит, выполнить программу
для каждого теста из всего набора тестов и убедиться, что нет
ошибок.
Тестирование программы с применением всего множества
возможных наборов исходных данных называют исчерпывающим.
По определению, если при исчерпывающем тестировании не
обнаружено ошибок, то программа корректна.
16.
Попытаемся оценить, сколько нужно выполнить тестов приисчерпывающем тестировании.
Пусть <x, y> тест, т. е. y= F(x) т. к. F: X Y, где X множество наборов исходных данных или область
определения задачи, или множество множеств исходных
данных программы. То X количество множеств исходных
данных программы, используемых при одном выполнении
программы, и ,следовательно, число тестов есть X .
Возьмем простой пример:
max(x,y) = if x>y then x else y в этой задаче max(a,b) = ifa>b
then a
17.
x =<a,b>a R, b R
y {a,b} и y=a если a>b
y= b если a b
18.
X ={<a, b> a R,b R т. е. на практике R RЭВМ и,
следовательно,
X= {<a, b> a RЭВМ b RЭВМ } при этом RЭВМ 168 1010
и, следовательно, X 1020 таким образом нужно 1020 тестов.
Во вторых, исчерпывающее тестирование экономически не
выгодно.
Пусть 1 сек 106 тестов, следовательно, 1020 106 получим 1014
сек - время тестирования, а 1 сутки = 24 60 60 = 1.5 105 сек,
следовательно, 1014 (1.5 105) 6.7 109суток 6.7 3 106 , т. к. 103сут
3 года.
19.
Даже если ограничится каким - то подмножеством,на наш взгляд представительным по отношению к
исчерпывающему тестированию, мы можем позволить
себе тестировать - сутки, месяц, два , но не более.
Может быть исчерпывающее тестирование “белым
ящиком” дает число тестов меньше чем тестирование
“черным ящиком”? Действительно, в примере на max
нужно всего два теста: один на путь a>b - истина ,
другой на путь a>b-ложно.
Такой фрагмент:
20.
_________________________________________________A
for i:= to n do
a1
if a[i] > b[i]
a2
then max[i]:= a[i]
a3
else max[i]:=b[i]
a4
_______________________________________________
_____B
21.
Путь программы от А до В - последовательность операторов от (.)А до (.) В. Очевидно, что путь от А до В это - а1а2С1а1а2С2а1а2С3 ...
а1а2Сnа1 , где Сi - это или а3 или а4. Значит, при одном и том же n,
общее число различных путей из (.) А до (.) В - это 2n . Все пути
нужно протестировать, следовательно, нужно 2n тестов. Поэтому
исчерпывающее тестирование никогда не применяется в серьезных
программах. Его место занимают методы тестирования:
1) убеждающее (убедительно демонстрирующее отсутствие ошибок и
абсолютно доказывающее наличие ошибок);
2) экономически выгодное.
К методам тестирования по “черному ящику” принадлежат:
1). Метод эквивалентных разбиений;
2). Метод граничных значений;
3). Метод предположение об ошибке.
22.
1.Метод эквивалентных разбиений.
Определение: Два теста эквивалентны <x1, y1> <x2, y2>, если оба
обнаруживают одну и туже ошибку.
Определение: Множество эквивалентных между собой тестов называют
классом эквивалентности.
Таким образом, если T = {<x,y>} полный набор тестов для исчерпывающего
тестирования, то T = T1 T2 ... Tn , где
Ti Tj =0 и называются
классами эквивалентности. Нет необходимости брать каждый тест из T и
проверять программу. Поскольку мы утверждаем, что любой тест из Тi
находит одну и ту же ошибку, то достаточно взять из Ti один и только один
тест tji Ti, где tji=<xji,yji> , т. е., чтобы протестировать программу вместо Т
нужно взять n тестов, ровно столь сколько классов эквивалентности.
Возникает вопрос, сколько классов эквивалентности нужно вводить? Как
минимум ровно столько, сколько ошибок. Возникает новый вопрос- кто
знает сколь ошибок в программе? Поэтому метод разбиений на классы
эквивалентности является методом не строгим, это эвристический метод.
23.
Во-первых, т. к. T= {<x, y>}, а Ti T, следовательно,Ti = {<xi, yi>} {<x, y>} = T или множество X =X1 X2 ... Xn, Xi Xj
=0. Относительно разбиения Yi этого сказать нельзя
Y=
Y1 Y2 ... Yn , Yi Yj 0.
Если Xi Xj 0, следовательно, существует два класса эквивалентности
тестов, которые с одной стороны находят одну и ту же ошибку, а с другой
стороны - два разные, но согласно определению эквивалентности Xi и Xj
- один класс.
Поэтому впредь мы будем разбивать на классы эквивалентности не тесты
, а множества множеств исходных данных, т. к. они однозначно
определяют классы эквивалентности.
24.
Во вторых, программа обрабатывает как корректные данные измножества определения, так и не корректные, вне множества определения
задачи.
По этому наряду с множеством Х рассматривают множество X неправильные данные, и разбиению подвергают как Х, так и X .
Первоначально множества Х и X разбиваются на классы эквивалентности этот шаг называют разбиением на классы.
25.
Затемиз каждого класса выбирают представителя - это шаг называют
проектированием тестов.
Программа выполняется для всех спроектированных тестов и только для них.
Пример:
Задача:
Разработать программу, которая для трех заданных чисел дает один из
следующих ответов:
1). “Не образуют”, если числа не являются длинами отрезков, или , в противном,
случае не образуют сторон треугольника;
2). “Образуют равносторонний”, если числа суть длины сторон равностороннего
треугольника;
3). “Образуют равнобедренный прямоугольный треугольник”;
4). “Образуют равнобедренный непрямоугольный треугольник”;
5). “Образуют разносторонний прямоугольный треугольник”;
6). “Образуют разносторонний непрямоугольный треугольник”,
если числа - длины сторон отрезков, и отрезки образуют соответствующий
треугольник.
26.
Решение:Формальная постановка задачи:
Пусть а - первое число, а R, b - второе число, b R, c - второе число, c R
и X = {<a, b ,c> R3 }.
Для построения классов эквивалентности проанализируем множество Х.
Область определения задачи - R3. Особыми свойствами
b
множество Х не обладает, за исключением , если a>0, b>0,
c>0 ,то числа - длины треугольника, т. е. X= X1 X2, где
X1 = { <a,b,c>, a>0, b>0, c>0 } и X2 =X\X1. Мы можем
разбить множество Х1 на два класса: X11 = { <a, b ,c> треугольник не существует} и X12 = { <a, b, c> a
c
X=
треугольник существует}. Следовательно,
a + c>b и
X11 X12 X2, где X11 ={<a, b, c> a+b>c и
b+c>a}, X12 =X1\X11, X2 = X\(X11 X12).
27.
Затем проанализируем множество Y. Элементов во множествеY - шесть.
Следовательно, можно выделить шесть классов: Х1 Х2 Х 3 Х4 Х5 Х6 ,
т. к. не существует события, когда треугольник существует и не существует, или
если треугольник равносторонний , то он не может быть неравнобедренным и т.
д. и, следовательно, Xi Xj и Xi = X.
28.
Опишем каждое множество Xi :1) f(Х1 ) = 1 тогда Х1 = {<a, b, c> <a, b, c>,но (a + b >c и a + c >b
и b +c >a), или
(a<0 или b<0 или c<0) };
2) f(Х2 ) = 2 тогда Х2 ={ <a, b, c> a = b = c, a,b,c>0, };
3) f(Х3 ) = 3 тогда Х3 = { <a, b, c > a = b
a2 + b2 = c2 или
a = c и a2 +c2 = b2 или
b =c и b2 + c2 =a2 , a,b,c>0, };
4) f(Х4 ) = 4 тогда Х4 = { <a, b, c >
a = b и a2 + b2 c2 или
a = c и a2 +c2 b2 или
b =c и b2 + c2 a2 , a,b,c>0, };
5) f(Х5 ) = 5
тогда Х5 ={ a2 + b2 = c2 или a2 +c2 = b2
или b2 + c2 = a2
a,b,c>0, };
f(Х6 ) = 6 тогда Х6 = { <a, b, c > ,a b и a2 + b2 c2 или a c и a2 +c2 b2 или b c и b2 +
c2 a2 , a, b , c>0 , }.
Где i - это i -тый ответ, который должна давать программа, = (a + b >c и a + c >b и
+c >a) - условие существования треугольника.
Используем формулы связи.
b
29.
Можно разделить:Х1 = Х11 Х12 , где Х11 = {<a, b, c >, a<0 или b<0 или c<0 }
Х12 = {<a, b, c> a, b,c >0, но (a + b >c и a + c >b и b +c >a)};
2 2 2
Х3 = Х31 Х32 Х33 , где Х31 = {<a, b, c >, a = b и a + b = c , a,b,c>0, },
2 2 2
Х32 = { <a, b, c >, a = c и a +c = b , a,b,c>0, },
2 2 2
Х33 = { <a, b, c >, b =c и b + c =a , a,b,c>0, }.
Очевидно, Х31 Х32 0 и Х31 Х33 0 и Х33 Х32 0 и точно также можно представить
Х4 = Х41 Х42 Х43 и Х5 = Х51 Х52 Х53 , а Х2 и Х6 не делятся.
30.
Теперь после построения классов эквивалентности, можем перейти кпостроению тестов для каждого из них:
1) Х11 - t1 = <(-1, -2, -3), 1>;
2) Х12 - t2 = <(1, 2, 3), 1>;
3) Х2 - t3 = <(2, 2, 2), 2>;
4) Х31 - t4 = <(3, 3, 3 2 ), 3>;
5) Х32 - t5 = <(4,4 2 , 4), 3>;
6) Х33 - t6 = <(5 2 , 5, 5), 3>;
7) Х41 - t7 = <(2, 2, 3), 4>;
8) Х42 - t8 = <( 3, 4, 3), 4>;
9) Х43 - t9 = <(5, 4, 4), 4>;
10) Х51 - t10 = <(3, 4, 5), 5>;
11) Х52 - t11 = <(10, 6, 8), 5>;
12) Х53 - t12 = <(9, 5, 12), 5>;
13) Х6 - t13 = <(2,3, 4), 6>.
Рекомендуется тесты выбирать таким образом , чтобы можно было просто
выполнить ручной расчет.
31.
Правильные и неправильные классы эквивалентности.Областью определения решения задачи Х мы называем множество исходных
данных программы. Само понятие “область решения задачи” относительно , а
не абсолютно. Так, в задаче о треугольнике область, решения задачи можно
считать только те числа, которые являются длинами сторон треугольника, а
остальные числа не включать в Х, т. е. относить к дополнению Х.
Таким образом, все множество данных, подаваемых на вход программы, делится
на два подмножества: Х - область решения задачи (множество исходных данных)
и X - прочие данные.
32.
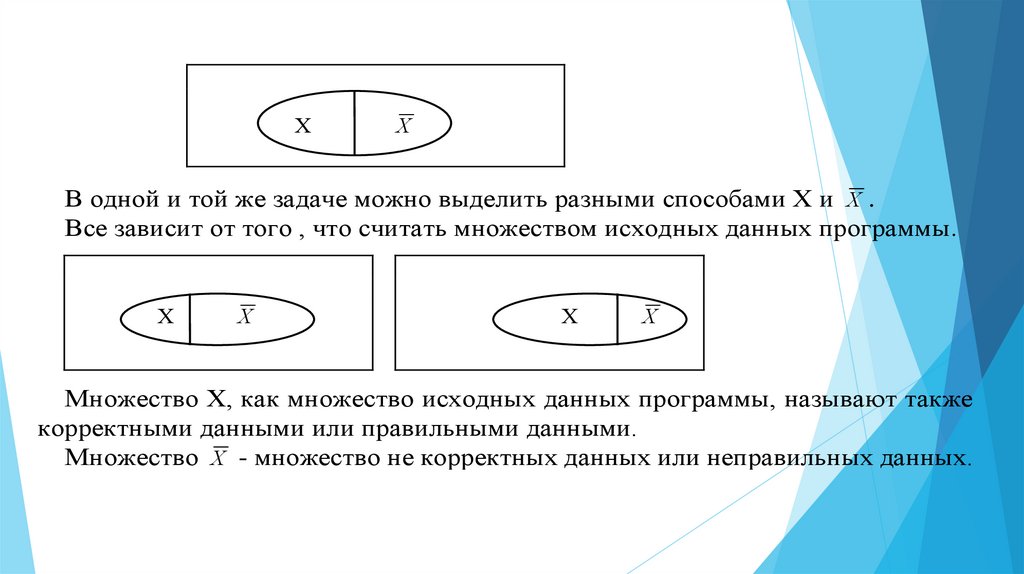
ХX
В одной и той же задаче можно выделить разными способами Х и X .
Все зависит от того , что считать множеством исходных данных программы.
Х
X
Х
X
Множество Х, как множество исходных данных программы, называют также
корректными данными или правильными данными.
Множество X - множество не корректных данных или неправильных данных.
33.
Начинающие программисты часто не обращают внимания на тот факт,что почти любая программа может начать выполнение для не корректных
данных, т. е. для данных которые не являются ее исходными данными.
Часто поведение программы на множестве правильных данных
предсказуемо, в то время как на множестве не правильных данных непредсказуемо в этом случае.
Поэтому любая программа должна быть защищена от не корректных
данных. Если это требование не выполняется программистом, то о нем
судят не очень высоко с точки зрения его квалификации.
Но защита программы от неправильных данных означает наличие
дополнительной части алгоритма, контролирующей корректность
исходных данных. И эта часть должна также быть оттестирована.
34.
Мы рассмотрели метод “Разбиение на классыэквивалентности” относительно множества правильных
данных. На его основе :
1). Получили правильные классы эквивалентности;
2). Для каждого класса спроектировали тест.
Теперь должны расширить метод на неправильные данные
и тем самым научиться выделять:
1). Неправильные классы эквивалентности;
2). Проектировать тесты.
35.
Нужно отдавать себе отчет, из каких элементов состоит множество X .Пусть U - универсальное множество данных, X R - некоторое пространство
U = Rn (U\Rn) = X (Rn\X) (U\Rn), X = X Rn X U, где X Rn= (Rn\X) и
X
U= (U\Rn). Множество X Rn - это данные неправильные, но они из того же
множества, что и правильные данные.
Пример:
X=[3,10] тогда X = (- , 3) (10, + ).
Множество X U - это данные неправильные и не принадлежат Rn.
Пример:
х [3, 10] , а X U строки, логические данные и т. д.
Очевидно, что программа на языке Паскаль системно защищена от
тестирования данных X U, поэтому имеет смысл защищаться только от X Rn. При
создании классов эквивалентности нужно придерживаться следующих
рекомендаций:
36.
1). Если есть возможность разложить X Rn на классы на основе описания X, Yили F, то применяйте тот же метод, что и для множества Х;
2). Если это сделать не просто , то будем считать, что каждое предложение
спецификации программы позволяет выделить некоторую ось ОХi в
пространстве Rn.
Как можно выделять классы:
1). Если спецификация определяет непрерывный интервал [a, b], то следует
иметь три класса эквивалентности :
а) неправильный (- , a);
б) неправильный (b, );
в) правильный [a, b];
2). Если спецификация определяет некоторый дискретный интервал
(числовой), то следует также иметь три класса эквивалентности , такие же как в
пункте 1, но для дискретных интервалов;
3). Если спецификация определяет нечисловой интервал, а некоторое
множество значений (7 элементов) , то следует иметь столько правильных
классов эквивалентности сколько элементов во множестве и один неправильный
класс эквивалентности (элемент вне определения множества).
4). Если спецификация определяет множество иным способом , чем в
пунктах 1, 2 и 3, то нужно иметь хотя бы один класс правильных данных и
один класс неправильных данных.
37.
Например:Если спецификация говорит, что слово должно начинаться с буквы А, то:
а) правильные данные: слово начинается с А;
б) неправильные данные : слово не начинается с А.
5). Если есть основание вводить новый класс - введите.
Пример:
Требуется подсчитать сколько студентов мужского и женского пола имеют
достаток : а) 0 - 400,
б) 400 - 800,
в) 800 - 1000,
и лиц:
а) успевающих (нет 2, но есть 3),
б)хорошо успевающих (одна - две четверки и без троек
и двоек),
в) отличники,
г) неуспевающие,
о каждом студенте известно :
а) фамилия имя отчество (ФИО - только русские буквы и пробел),
38.
Если рассматривать все множество исходных данных задачи, то мы имеемпятимерное пространство. Чтобы в нем построить правильные классы
эквивалентности , нужно сначала выделить в нем подмножество символов
образующих ФИО, в нем два подмножества: муж и жен, в каждом из них
три подмножества по доходу и далее разделить на
подмножества по успеваемости, и мы, таким образом,
получаем 24 подмножества. Это для такой простой
задачи, а для практических задач это число будет
существенным. Поэтому рассматривают не все
множество исходных данных, а каждое подмножество отдельно, т. е. по осям.
39.
Таким образом, получаем классы:1). Русские буквы и пробел, образующие ФИО (правильный);
2). Символы не образующие ФИО (неправильный);
3). [жен] (правильный);
4). [муж] ( правильный);
5). [дев] (неправильный);
6). [0 - 400 ] (правильный);
7). [400 - 800] (правильный);
8). [ 800 - 1000] (правильный);
9). (- , 0) ( неправильный);
10). ( 1000, ) ( неправильный);
11).[2] (правильный);
12). [3] (правильный);
13). [4] (правильный);
14). [5] (правильный);
15). [6] (неправильный).
40.
Строим тесты руководствуясь:1). Как можно большее количество правильных классов эквивалентности покрыть одним тестом,
но не единственным;
2). Каждый неправильный класс эквивалентности покрывается отдельным тестом, а иначе одна
ситуация будет протестирована, а другая - нет.
Тесты:
t1 = Петров Иван Сергеевич
муж
450
4
t2 = Сергеева Татьяна Петровна
жен
300
2
t3 = Терехова Инна Петровна
жен
850
5
41.
t4 = Харитонов Илья Владимировичмуж
410
3
t5 = Derbenev Игорь Семенович
муж
200
3
t6 = Сергеева Татьяна Ивановна
дев
456
4
t7 = Терехова Инна Петровна
жен
-200
5
42.
t8 = Сидорова Галина Петровнажен
2000
4
t9 = Петров Иван Сергеевич
муж
450
6
Анализ граничных условий.
Граничные условия - это ситуация , возникающая непосредственно на, выше или
ниже границ входных и выходных классов эквивалентности . Анализ граничных
значений отличается от эквивалентного разбиения в двух отношениях.
43.
Во-первых, выбор любого элемента в классе эквивалентности в качествепредставительного при анализе граничных значений осуществляется таким образом,
чтобы проверить тестом каждую границу этого класса.
Во-вторых, при разработке тестов рассматриваются не только входные условия, но и
пространство результатов , т. е. выходные классы эквивалентности.
Рассмотрим несколько общих правил этого метода:
1). Построить тесты для границ области и тесты с неправильными входными данными
для ситуаций незначительного выхода за границы области, если входное условие
описывает область значений. Например, если правильная область входных значений есть
-2,0 и 2,0, то следует написать тесты для ситуаций -2., 2., 2.001, -2.001;
2). Построить тесты для минимального и максимального значений и тесты, большие и
меньше этих значений, если входное условие удовлетворяет дискретному ряду значений.
Например, если входной файл содержит от 1 до 255 записей, то получить тесты для 0, 1,
255, 256 записей;
3).Использовать правило один для каждого выходного условия.
44.
Например, если программа вычисляет ежемесячный расход и если минимум расходасоставляет 0 рублей и максимум 1 234 500, то построить тесты, которые вызывают
расходы 0 рублей и 1 234 500 рублей, Кроме того, построить, если это возможно тесты,
которые вызывают отрицательный расход и расход больше 1 234 500. Заметим, что
важно проверить границу результатов, поскольку не всегда границы входных областей
представляют такой же набор условий, как и границы выходных областей (например,
при рассмотрении программы вычисления синуса). Не всегда также можно получить
результат вне выходной области. Но тем не менее, стоит рассмотреть эту возможность.
4). Использовать правило два для каждого выходного данного, например, если
программа отображает на экран аннотации на книги в зависимости от входного запроса,
но ни как не более четырех аннотаций , то построить тесты такие , чтобы программа
отображала ноль, одну, четыре аннотации и тест, который мог бы вызвать выполнение
программы с ошибочным отображением - 5 аннотаций;
45.
5). Если вход и выход программы есть упорядоченное множество, тососредоточьте внимание на первом и последнем элементах этого множества;
6). Попробуйте свои силы в поиске других граничных условий.
Построим тесты на примере треугольника:
t3 = <(2, 2, 2), 2>; (равносторонний)
t31 = <(1.99, 2,2), 4>; (равнобедренный)
t32 = <(2.01,2 , 2), 4>; (равнобедренный)
t33 = <(2, 1.99, 2), 4>;
t34 = <(2, 2.01,2), 4>;
t35 = <(2,2 , 1.99), 4>;
t36 = <(2, 2, 2.01 ), 4>;
t7 = <(2, 2, 3 ), 4>;
t71 = <(1.99, 2, 3), 6>; (разносторонний не прямоугольный)
t72 = <(2.01, 2, 3), 6>;
t73 = <(2,1.99, 3), 6>;
t74 = <(2, 2.01, 3), 6>;
t4 = <(2, 2, 2 2 ), 3>; (равнобедренный прямоугольный)
t41 = <(1.99, 2, 2 2 ), 6>;
t42 = <(2.01, 2, 2 2 ), 6>;
и т д. по каждой “границе” множества.
46.
Анализ граничных значений, если он применяется правильно ,является одним из наиболее полезных методов проектирования
тестов. Однако он часто оказывается не эффективным из-за
того, что внешне выглядит простым и границы условия могут
быть едва уловимы, и следовательно, определение их связано с
большими трудностями.
Предположение об ошибке
Основная идея метода заключается в том, чтобы перечислить в
некотором списке возможные ошибки или ситуации, в которых
они могут появиться. Потом на основе этого списка составить
тесты. Например: ситуация - деление на ноль - значит нужно
подобрать данные для теста, дающие в знаменателе ноль.
47.
Рассмотрим в качестве примера тестированиепрограммы сортировки файла по убыванию, выделив
следующие ситуации:
Сортируемый файл пуст;
Сортируемый файл содержит только одно значение;
Все записи в сортируемом файле имеют одно и то же
значение;
Файл уже отсортирован.
Требуется перечислить те специальные случаи, которые
могут быть не учтены в спецификациях программы.
1.
2.
3.
4.
48.
Тестирование методами “белого ящика”Тестирование программы методами “белого ящика”
основано на знаниях логической структуры
программы. В отличие от методов “черного ящика”
тесты “белого ящика” разрабатываются после того,
как будет полностью создан текст программы.
49.
Первоначально рассмотрим вопрос об исчерпывающем тестировании.Пусть Х - множество исходных данных программы Р, а Y - множество
результатов, т. к. P : X Y, то y =P(x), для x X. Пусть р - элементарное
указание программы, т. е. указание, не содержащее конструкций ветвления,
выбора, цикла и не являющееся вызовом подпрограммы. Вызов
предопределенных подпрограмм или из стандартных библиотек подпрограмм
будем считать элементарным указанием. Для простоты оператор
GOTO
< метка > не содержится в программе.
Определим Sp = <p1, p2, ... , pk> - последовательность элементарных
указаний программы Р. Элементарное указание pi покрывается тестом <x, y>
, если pi Sp , порожденному программой Р. Также говорят, что тест <x, y>
покрывает путь Sp.
50.
Пример:Если (x>y и y>0 и z<0) то
пока z<0
z = z + (x + y)
иначе
z = x- y
программа:
51.
program prim1 (input, output);VAR
x, y, z : real;
p, t : text;
BEGIN
ASSIGN (p, ‘input.dat’);
ASSIGN ( t, ‘ output.dat’);
RESET (p);
REWRITE (t);
read(p, x, y, z);
if((x>y) and (y >0) and (z<0)) then
while (z<0) do
z := z + x +y
else
z: = y - x;
write (t, x, y, z);
CLOSE (p);
CLOSE (t);
END.
52.
Элементарные указания:p1 =ASSIGN (p, ‘input.dat’);
p2 =ASSIGN ( t, ‘ output.dat’);
p3 = RESET (p);
p4 = REWRITE (t);
p5 = read(p, x, y, z);
p6 =(x>y) and (y >0) and (z<0)
p7 = z<0
p8 = z := z + x +y
p9 = z: = y - x;
p10 = write (t, x, y, z);
p11 = CLOSE (p);
p12 = CLOSE (t);
53.
пути:S1 = <p1, p3> - открытие файла на чтение,
S2 = <p2, p4> - открытие файла на запись,
S3 = <p1, p2, p3, p4, p5, p6, p9, p11, p12> - ветвь без цикла,
S4 = <p1, p2, p3,p4, p5, p6, p7, p8, p10> - ветвь с циклом 1 такт,
S5 = <p1, p2, p3, p4, p5, p7, p8, p7, p8, p10> - ветвь с циклом
2 такт,
...
Sn+3 = <p1, p2, p3, p4, p5, p6, p7, p8, ... , p7, p8, p10, p11, p12> n -ый такт.
Очевидно, что при n число путей программы растет. Этот
пример еще раз показывает, что исчерпывающее тестирование не
приемлемо с точки зрения разумных подходов. Поэтому
исчерпывающее тестирование по “белому ящику” заменено на
метод покрытия элементарных указаний, метод покрытия всех
ветвей, метод покрытия элементарных условий.
54.
Метод покрытия элементарных указанийНеобходимо столько тестов, сколько их достаточно, чтобы покрыть все
элементарные операторы.
Очевидно, что тесты, покрывающие пути S1 и S2, не покрывают указаний
p7, p8, p9, p10 и p11, p12. Поэтому нужны тесты, покрывающие пути S4 и S5,
т. к. при этом покрываются все элементарные операторы.
Обычно составляют таблицу тестов:
p1 p2 p3 p4 P5 p6 p7 p8 p9 p10 p11 p12
тесты
+ + + + + + - + + + + T1 =<(3, 2, 0), -1>
+ + + + + + + + - + + + T2 =<(3, 2, -10), 0>
из которой видно, как покрываются операторы.
Рекомендуется как можно меньше тестов. Тесты проектируются как на
множестве правильных данных так и на неправильных.
55.
Положительная сторона метода - возможностьпроверить все ли указания используются.
Негативная сторона метода - нельзя проверить
ошибки условия.
Например: тесты T1 и T2 не обнаруживают ошибку:
(x>y) and (y>z) and (0>z), и тест T3 = <(3, -4, -5), 2> зацикливает, только это обстоятельство и наводит на
размышления об ошибке.
56.
Метод покрытия всех ветвейРассмотрим:
if() then ... else ... или if() then ...
ветвь программы ветвь программы ветвь программы пустая
ветвь
и
for b:= op1 to op2 do
begin
op4
op5
end
1 ветвь - op1 op2 op4 op5 op3,
2 ветвь - op1 op2 , аналогично для while, repeat ... until, case.
Пусть А - начало конструкции, а В - ее конец.
57.
Ветвь - это минимум различных указаний и конструкциймежду точками А и В, которая принадлежит некоторому
пути программы, если в этой последовательности нет
указаний - это пустая ветвь. Между А и В может быть
несколько путей.
58.
p1p2
p3
p4
p5
p6
p7
p9
p8
p10
p11
p12
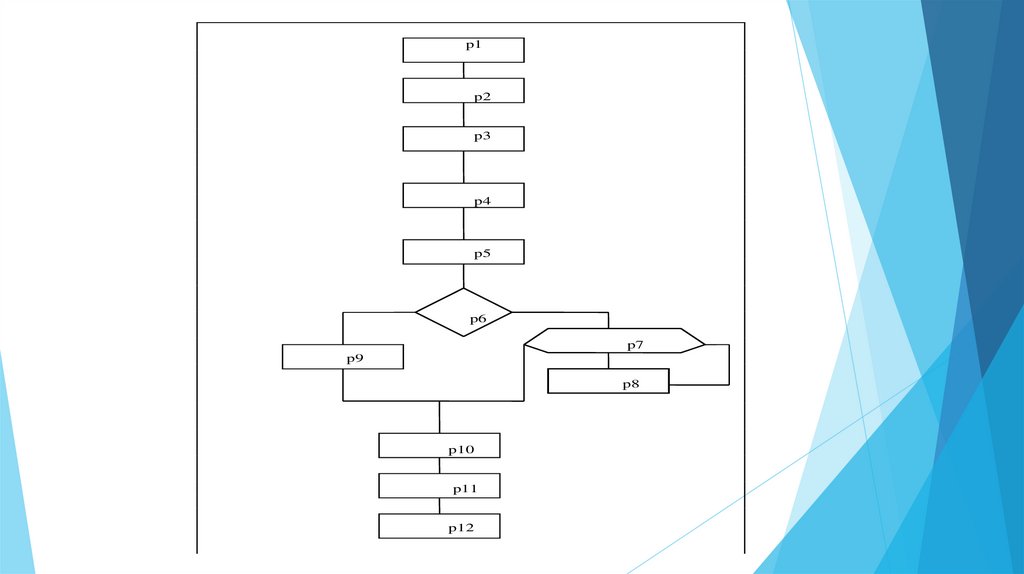
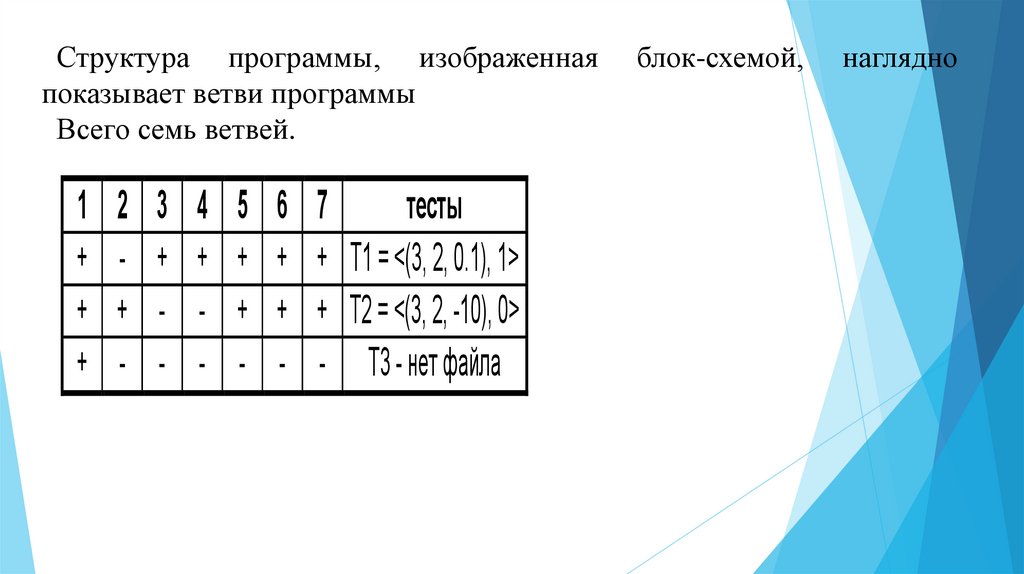
59.
Структура программы, изображеннаяпоказывает ветви программы
Всего семь ветвей.
1
+
+
+
2
+
-
3
+
-
4
+
-
5
+
+
-
6
+
+
-
7
тесты
+ T1 = <(3, 2, 0.1), 1>
+ T2 = <(3, 2, -10), 0>
- T3 - нет файла
блок-схемой,
наглядно
60.
Ветвь покрывается тестом, если при выполнении программы для этого тестауказания ветви использовались. Для покрытия всех ветвей выбирается наименьшее
количество тестов.
Обычно рекомендуется :
1) два теста на конструктор if;
2) для циклов :
а) тест на пустой цикл;
б) тест на не пустой цикл;
в) тесты для каждой точки выхода из цикла;
3) для case :
а) тест для каждой альтернативы;
б) тест на else;
в) тест для каждого дополнительного выхода из case.
Положительная сторона метода - обнаруживает все ли ветви покрыты, иначе,
например, бывают циклы условие, которых всегда ложно.
Негативная сторона метода - не отлавливает ошибки в условии.
61.
Метод покрытия элементарных условийУсловие
любая
форма
условного
выражения.
Элементарное условие - один операнд условного
выражения. Константы-операнды - особый случай. Они
предварительно и тщательно проверяются на правильность
записи. Согласно методу нужно столько тестов, чтобы
проверить, что каждое элементарное условие на этих тестах
имело истинное и ложное значение.
62.
Классификация ошибокПрограммист обязан знать:
1) источник ошибок;
2) классы ошибок;
3) как идентифицировать ошибку;
и обязан уметь:
1) локализовать место ошибки;
2) устроить так, чтобы не допустить новую ошибку.
Источники ошибок присутствуют на каждом этапе технологии
программирования.
На этапе постановки задачи допущенная ошибка имеет не
предсказуемые результаты. Источник - не понимание разработчиком
задачи заказчика, его поспешность перехода к последующим этапам, а
порой откровенное игнорирование этапа постановки.
63.
Как правило, игнорируют формальную и неформальную постановку задачистуденты, спешат очень самонадеянные и нечестные исполнители, не понимают задачу
неспециалисты.
Прежде чем переходить к этапу алгоритмизации, нужно неоднократно обсудить с
заказчиком , что он хочет. Самому сформулировать требования заказчика. В серьезных
задачах - оформить техническое задание.
Согласованная с заказчиком постановка задачи - основа спецификации программы(
письменно описать , что должна , и что не должна делать программа).
Спецификация программы - единственный критерий проверки на правильность
написанной программы.
Ошибки этапа алгоритмизации свидетельство низкой профессиональной подготовки
алгоритмиста: либо он слаб как математик, либо как разработчик алгоритмов, либо и
то и другое. Слабые алгоритмисты минуют этот этап и пытаются разработать
программу, минуя алгоритм. Это можно сделать либо для прозрачной задачи, либо для
задачи алгоритм, которой общеизвестен.
64.
При последующем проектировании программы так же возможны ошибки. Ихисточники - нечеткое выделение подзадач, в результате чего может быть пропущена
одна или несколько подзадач.
Пример:
В тексте встречаются русские и английские слова. Нужно собрать их в две таблицы
: русских и латинских слов.
Выделены подзадачи:
1) пропуск пробелов и “неслов”;
2) следующее слово, которое нужно вносить в таблицу выделенных слов ;
Проект:
<пропуск пробелов и “неслов”>
while <не конец файла> do
<следующее слово включить в таблицу >
<пропуск пробелов>
- нет подзадачи , что за слово!
На этапе кодирования ошибки - незнание языка, невнимательность, небрежность и т.
д.
65.
Локализация ошибокНапомним, что отладка - это процесс устранения ошибок, который имеет три этапа:
1) обнаружение признаков ошибки;
2) локализация ошибки;
3) исправление ошибки.
В первую очередь нужно установить класс ошибок: алгоритмическая или
семантическая. Для чего желательно перепроверить формальную постановку
задачи и проект программы. Если обнаружена здесь ошибка , то нужно исправить
ее и в программе. Возможно, это будут небольшие изменения , а возможно
программу придется переписывать заново.
Если характер ошибок не ясен, алгоритмическая это или семантическая, то
выдвигается несколько гипотез о причине ошибки.
Первая гипотеза, которую следует выдвинуть : правильно ли печатается результат (
быть может ошибки в операторах печати).
Вторая - правильно ли передаются программе (подпрограмме) исходные данные.
Быть может нарушен интерфейс со средой.
66.
Если эта гипотеза не подтверждается - выдвигаются другие гипотезы, ноуже с учетом логики алгоритма, с учетом наиболее вероятной ошибки.
Вначале можно использовать перечень возможных ошибок, который
может пополняться по мере накопления опыта:
1) ошибки ввода - вывода;
2) ошибки при обращении к функциям (подпрограммам);
3) ошибки при работе с циклами и переключателями;
4) ошибки при работе со строками;
5) ошибки в сравнениях ...
Ошибки при вводе:
1) неправильно размещены данные на носителях информации;
2) несоответствие типов форматов и данных;
3) конец файла обнаружен раньше, чем ожидался (недостаток данных);
4) не правильное указание файла в функциях открытия файла;
и т. д.
67.
Ошибки описания данных :1) при наличии в языке правил умолчания при описании данных - не правильная
инициализация, не правильный тип данных;
2)
нечеткое знание правил определения действия имен.
Ошибки при обращении к данным :
1) используются значения переменной, которая не определена;
2) выход индекса массива за его границы;
3) нецелочисленность индекса, если она допустима;
4) попытка обратится к памяти по неопределенному адресу.
Ошибки вычислений :
1) неаккуратность
использования различных типов данных в арифметических
выражениях;
2) деление на ноль, потеря точности, исчезновение порядка.
Ошибки при сравнениях :
1) сравнение разнотипных данных;
2) сравнение действительных чисел на равенство.
















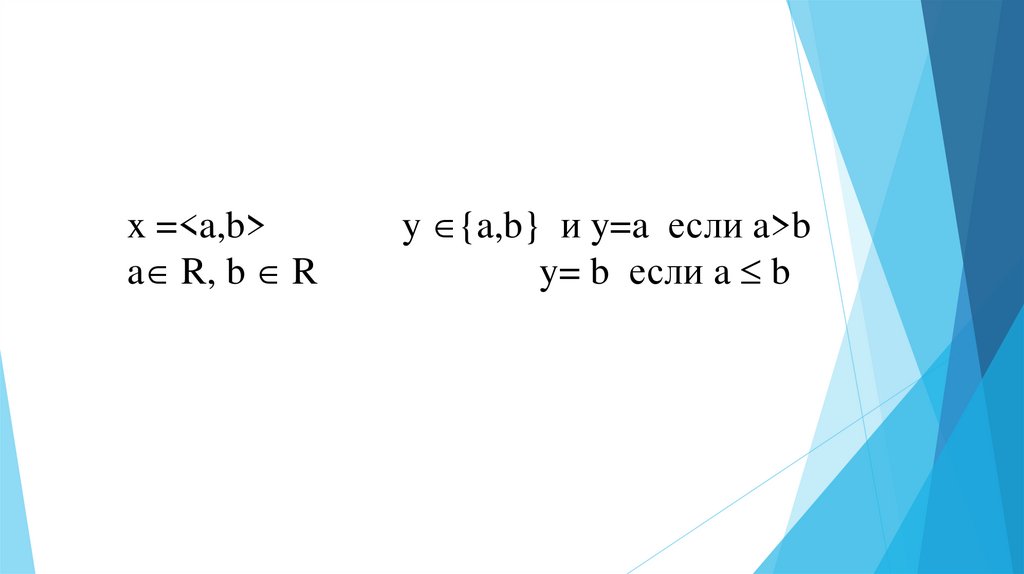















































 software
software








