Similar presentations:
Разработка урока по математике в 10 классе. Тема урока: «Нахождение углов в задачах по стереометрии»
1.
Разработка урока поматематике в 10 классе
Учителя высшей
квалификационной категории
МБОУ СОШ №7
г.Новосибирска
Чирковой Галины Васильевны
2.
Немного о себе:В школе №7 работаю с
1990 года.
Все эти годы преподаю в классах с
углубленным изучением математики,
60%моих учеников сдают экзамены на «5».
За все годы работы, «2», на экзаменах не
было.
3.
Тема урока: «Нахождение углов взадачах по стереометрии»
Цель: сформировать навыки нахождения углов в
стереометрических задачах С2 при подготовке
к ЕГЭ.
Задачи:
обобщение понятия углов между скрещивающимися прямыми,
между прямой и плоскостью, между плоскостями;
применение изученных определений, признаков и свойств при
решении задач;
развитие у учащихся умения адаптироваться в новой ситуации,
осознавать и определять свои возможности, искать ресурсы их
осуществления.
4.
Мотивация учебной деятельностиТема: «Нахождение углов в задачах по
стереометрии» связана с тем, что часть «С» ЕГЭ
содержит задания на нахождение отрезков и углов,
связанных
с
многогранниками,
поэтому
необходимо обратить внимание на следующие
объекты: прямая плоскость, прямая призма,
прямоугольный параллелепипед, куб.
5.
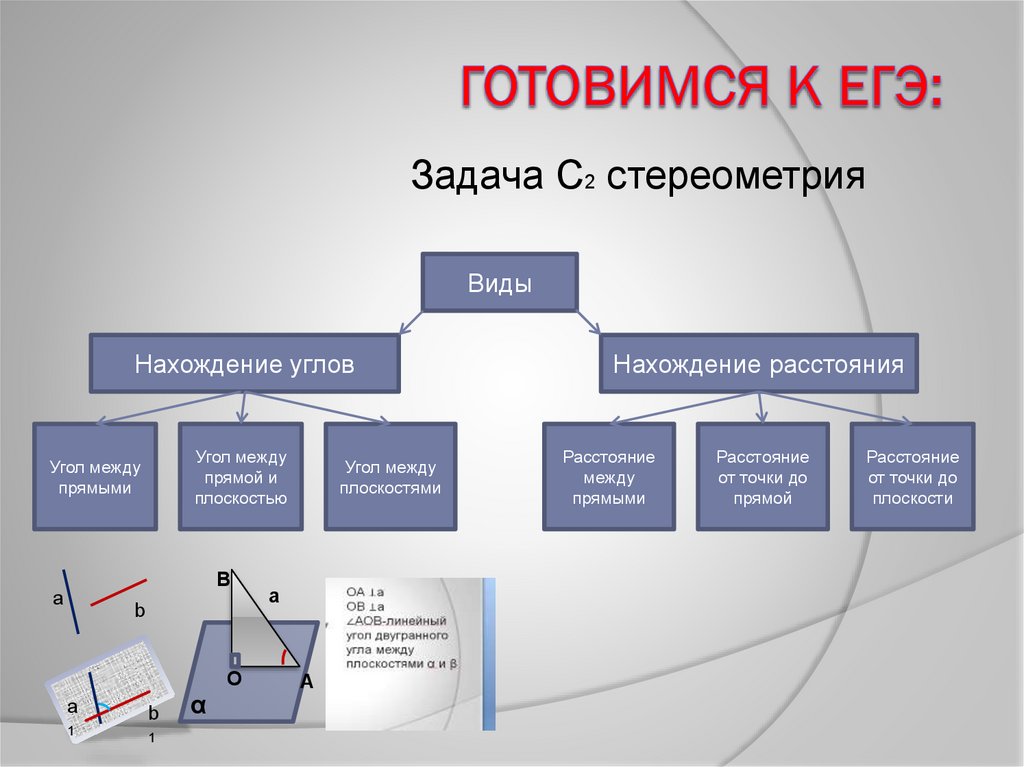
Задача С2 стереометрияВиды
Нахождение углов
Угол между
прямой и
плоскостью
Угол между
прямыми
В
а
b
O
а
b
1
1
α
Угол между
плоскостями
a
A
Нахождение расстояния
Расстояние
между
прямыми
Расстояние
от точки до
прямой
Расстояние
от точки до
плоскости
6.
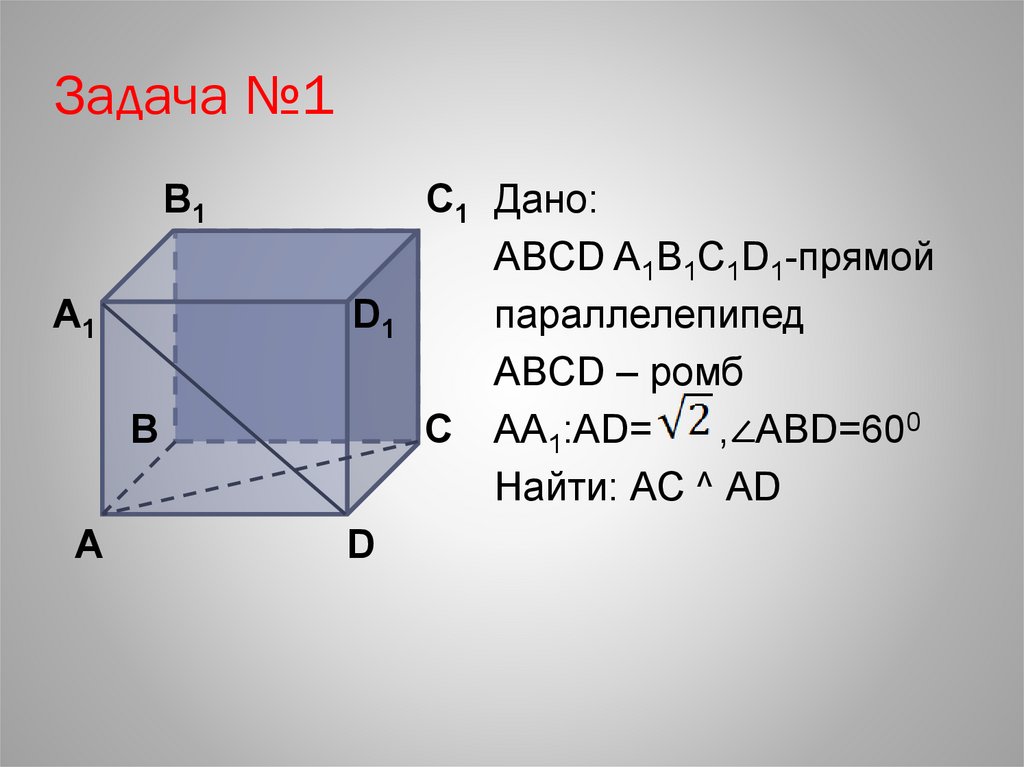
Задача №1B1
А1
D1
В
А
D
C1 Дано:
ABCD A1B1C1D1-прямой
параллелепипед
ABCD – ромб
С АА1:АD=
,∠ABD=600
Найти: АС ^ АD
7.
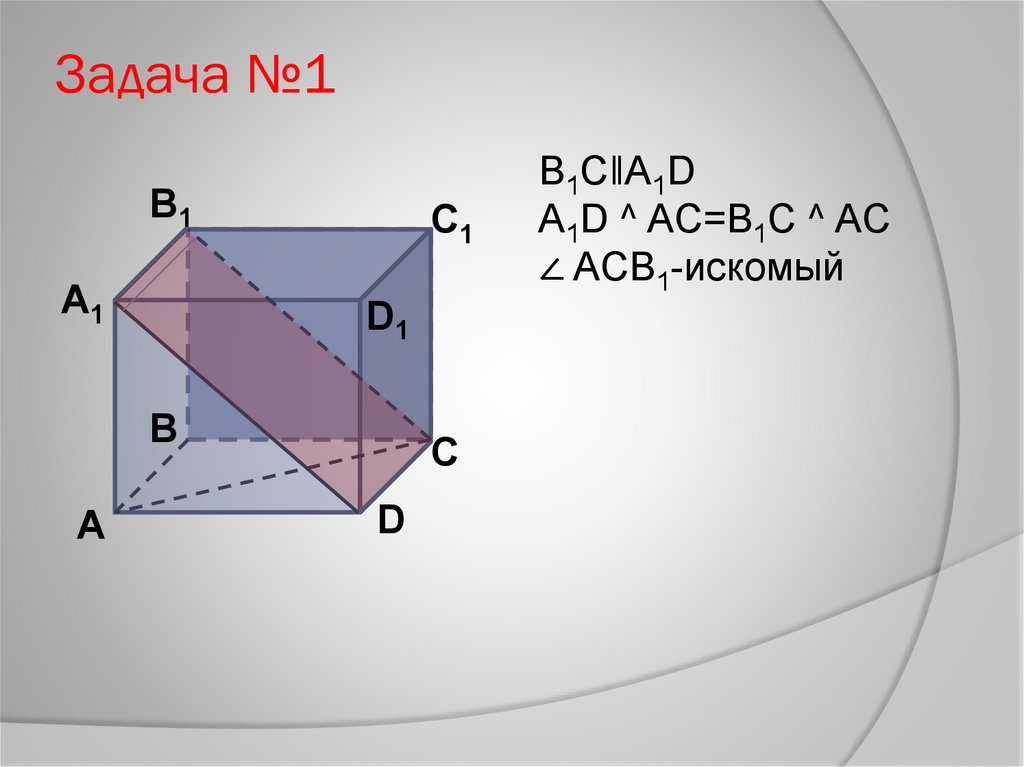
Задача №1B1
A1
C1
D1
B
A
C
D
В1С‖А1D
A1D ^ AC=B1C ^ AC
∠ ACB1-искомый
8.
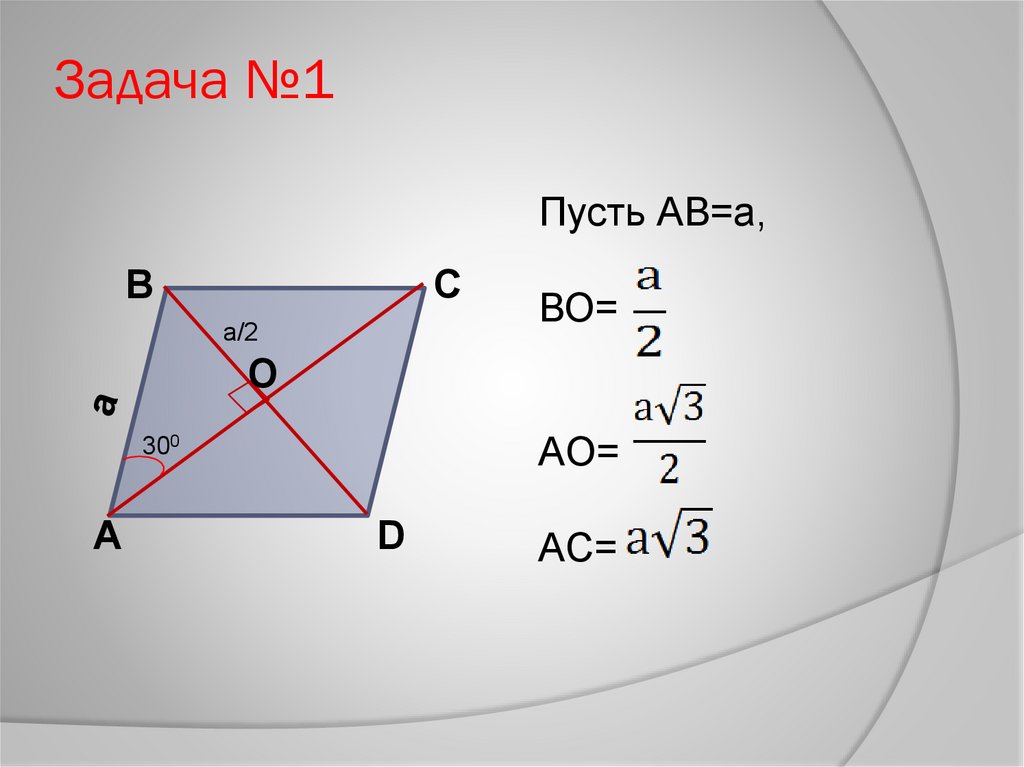
Задача №1Пусть АВ=а,
В
С
a/2
ВО=
O
300
А
AO=
D
AC=
9.
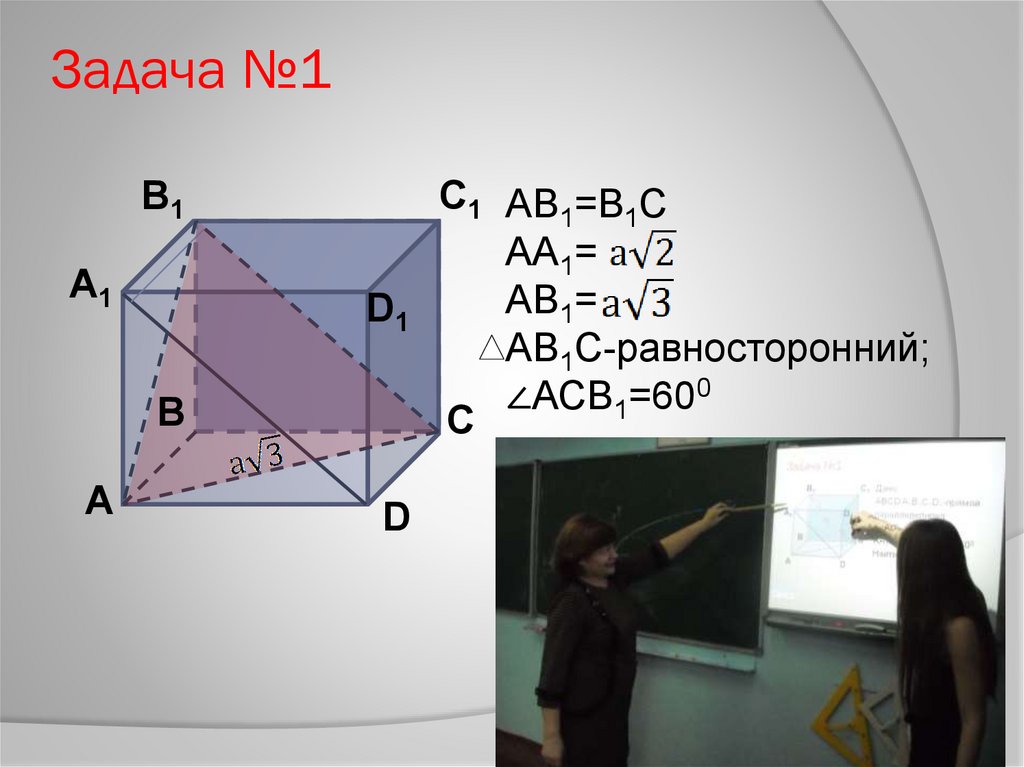
Задача №1B1
A1
D1
B
A
D
C1 AB1=B1C
AA1=
AB1=
AB1C-равносторонний;
∠АСВ1=600
C
10.
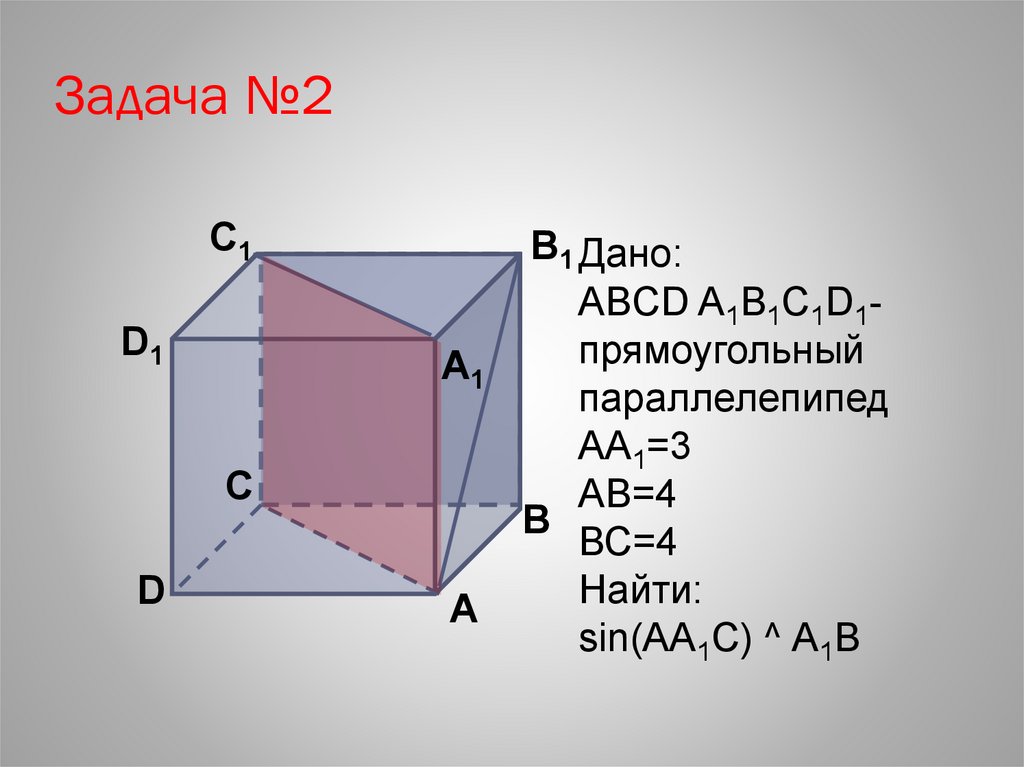
Задача №2С1
D1
A1
C
D
A
B1 Дано:
ABCD A1B1C1D1прямоугольный
параллелепипед
АА1=3
АВ=4
B
ВС=4
Найти:
sin(AA1C) ^ A1B
11.
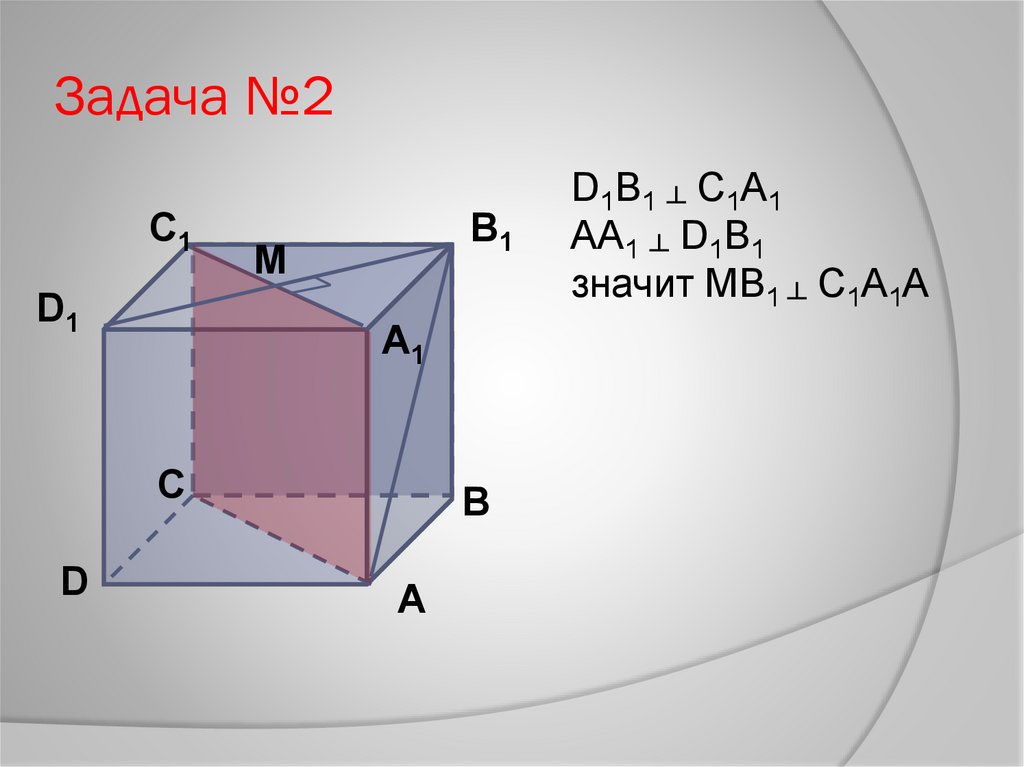
Задача №2С1
D1
B1
M
A1
C
D
B
A
D1B1 ┴ C1A1
AA1 ┴ D1B1
значит МВ1 ┴ С1А1А
12.
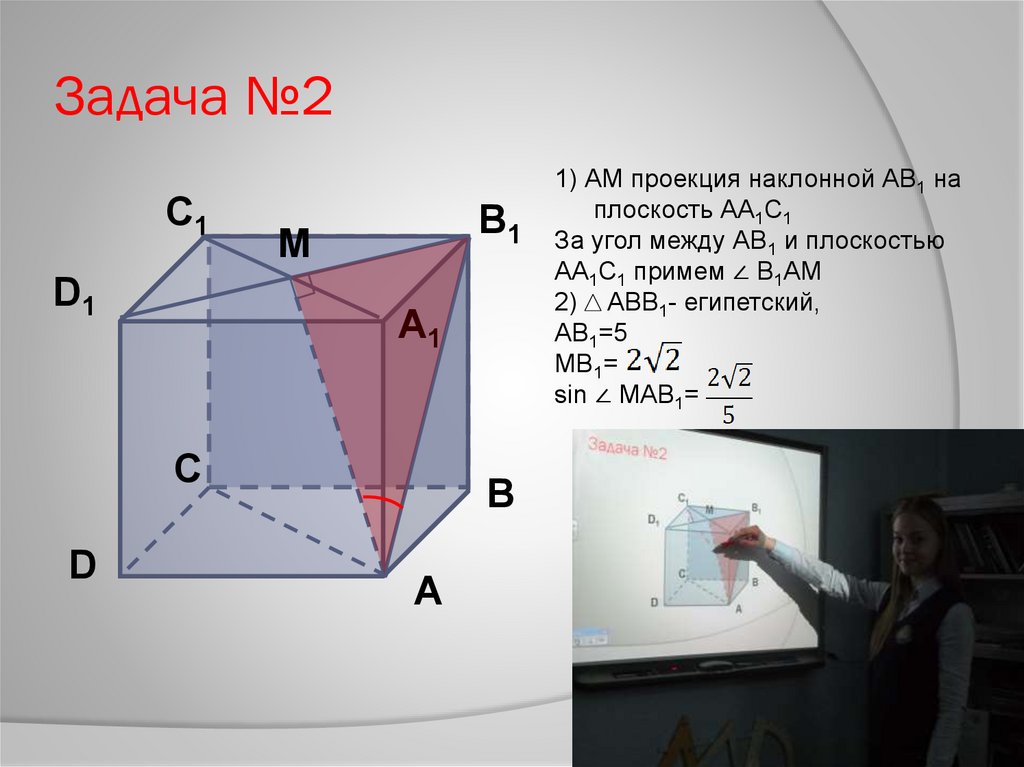
Задача №2С1
D1
B1
M
A1
C
D
B
A
1) АМ проекция наклонной АВ1 на
плоскость АА1С1
За угол между АВ1 и плоскостью
АА1С1 примем ∠ В1АМ
2) АВВ1- египетский,
АВ1=5
МВ1=
sin ∠ MAB1=
13.
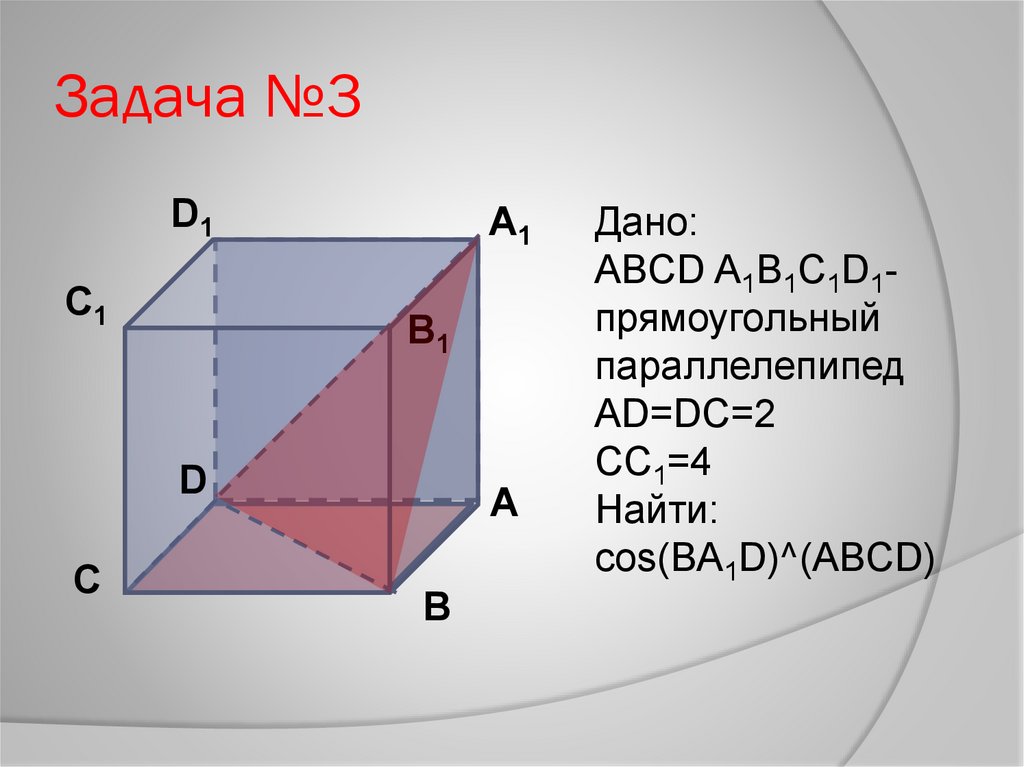
Задача №3D1
C1
A1
B1
D
C
A
B
Дано:
ABCD A1B1C1D1прямоугольный
параллелепипед
АD=DC=2
CC1=4
Найти:
cos(BA1D)^(ABCD)
14.
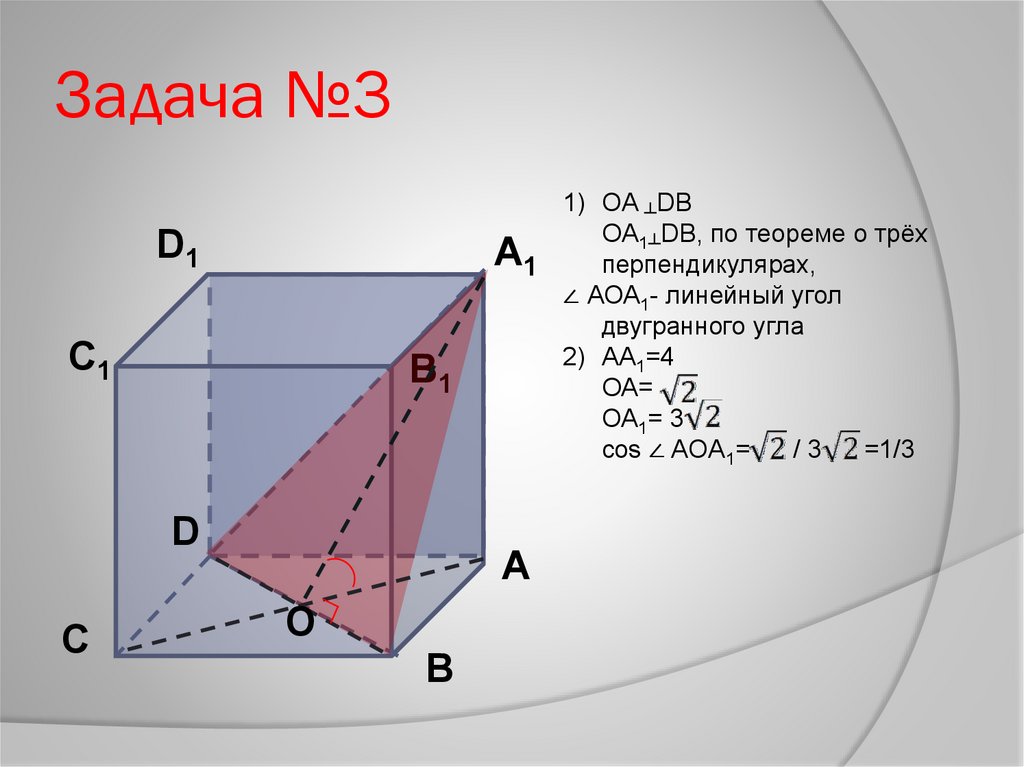
Задача №3D1
C1
B1
D
C
1) OA ┴DB
OA1┴DB, по теореме о трёх
A1
перпендикулярах,
∠ АОА1- линейный угол
двугранного угла
2) АА1=4
ОА=
ОА1= 3
cos ∠ AOA1=
/3
=1/3
A
O
B





 mathematics
mathematics








