Similar presentations:
Решение задач с параметром с использованием координатно-параметрической плоскости
1.
РЕШЕНИЕ ЗАДАЧ С ПАРАМЕТРОМС ИСПОЛЬЗОВАНИЕМ
КООРДИНАТНО - ПАРАМЕТРИЧЕСКОЙ
ПЛОСКОСТИ.
Гайкович Э.Б
ГБОУ СОШ № 4 Кусто
2.
).?
ЗАДАЧА №1
При каких а уравнение
имеет ровно один корень на отрезке
Решение
1)
=0
3.
а=ха
а
х
а=6-х
х
4.
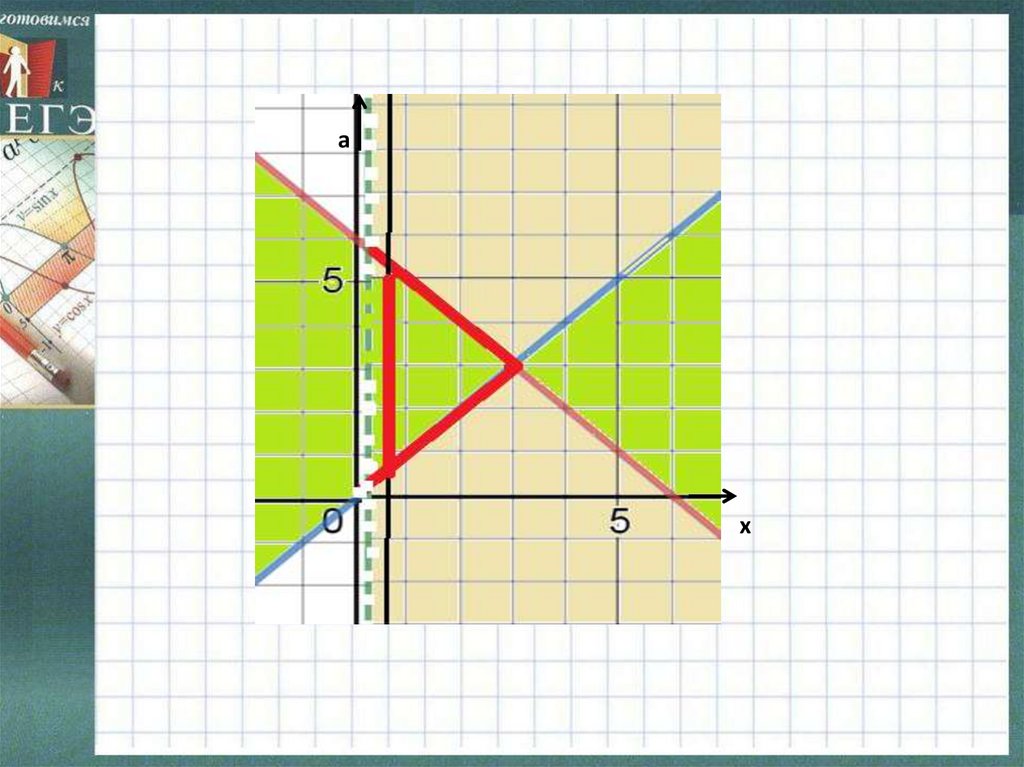
2)Покажем решения на плоскости (х;а):
5.
ах
6.
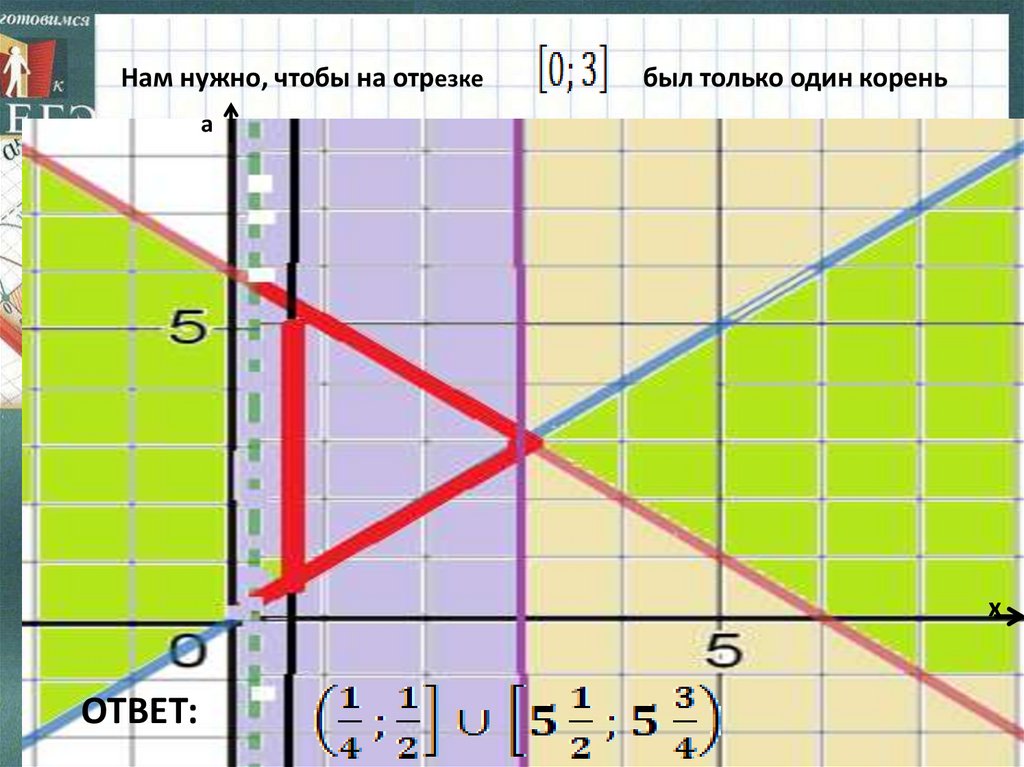
Нам нужно, чтобы на отрезкебыл только один корень
а
х
ОТВЕТ:
7.
ЗАДАЧА №2При каких а уравнение
Имеет единственное решение на отрезке
Решение:
Уравнение равносильно
системе:
Решим неравенство
методом интервалов
?
8.
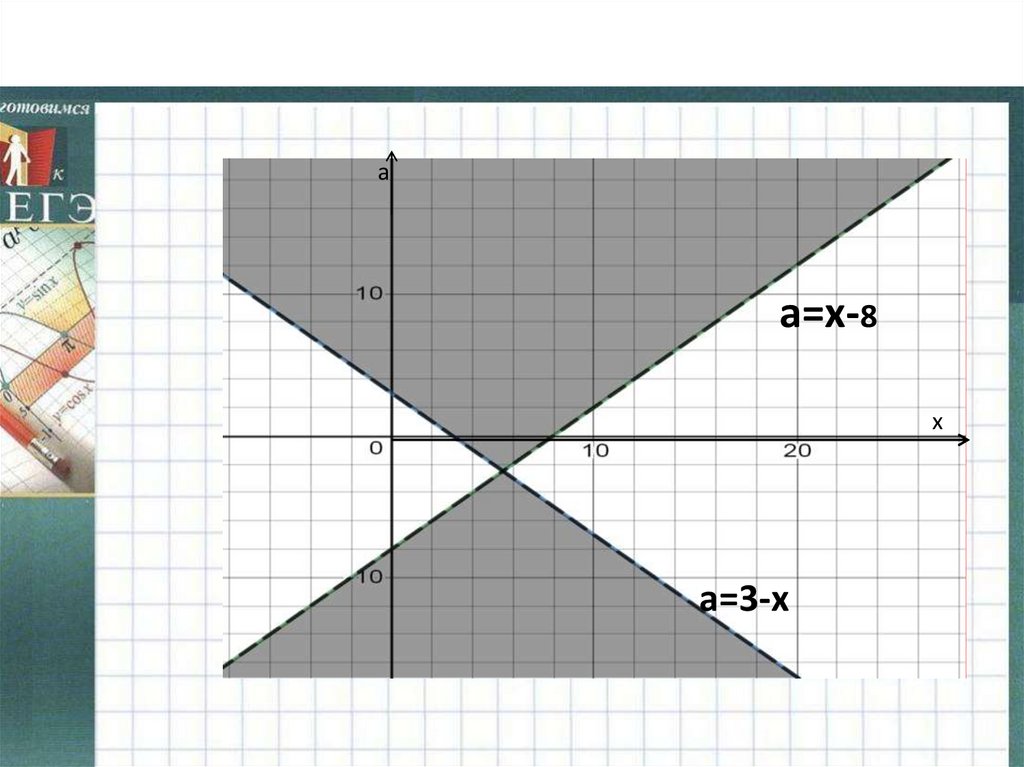
аа=х-8
х
а=3-х
9.
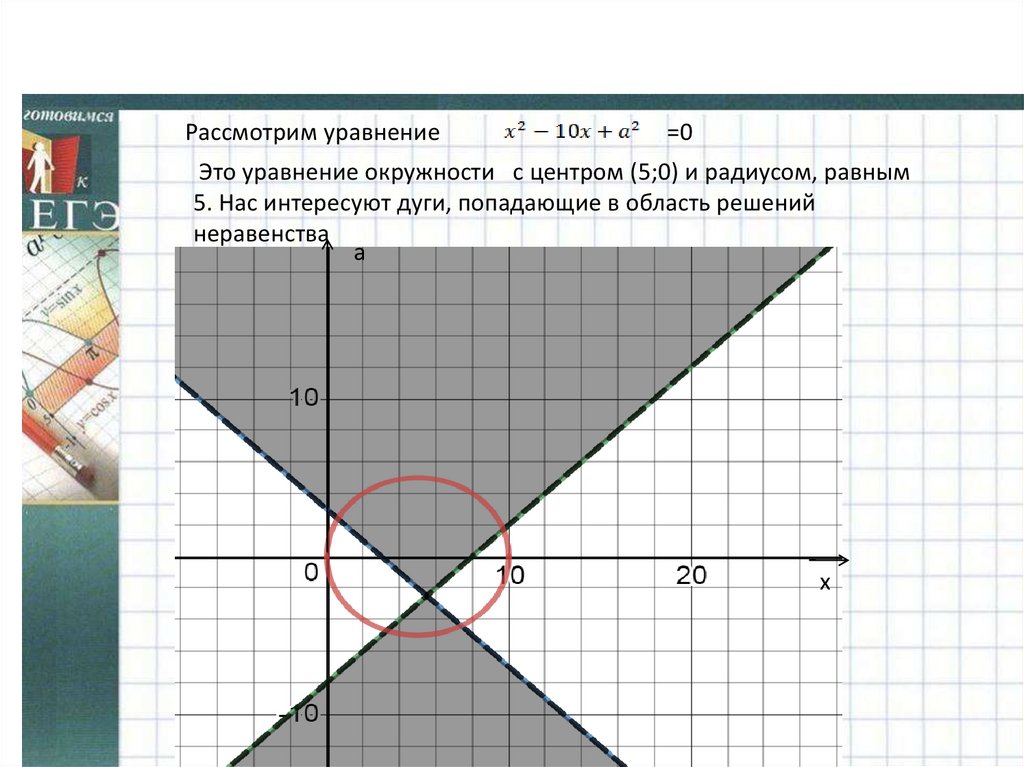
Рассмотрим уравнение=0
Это уравнение окружности с центром (5;0) и радиусом, равным
5. Нас интересуют дуги, попадающие в область решений
неравенства
а
х
10.
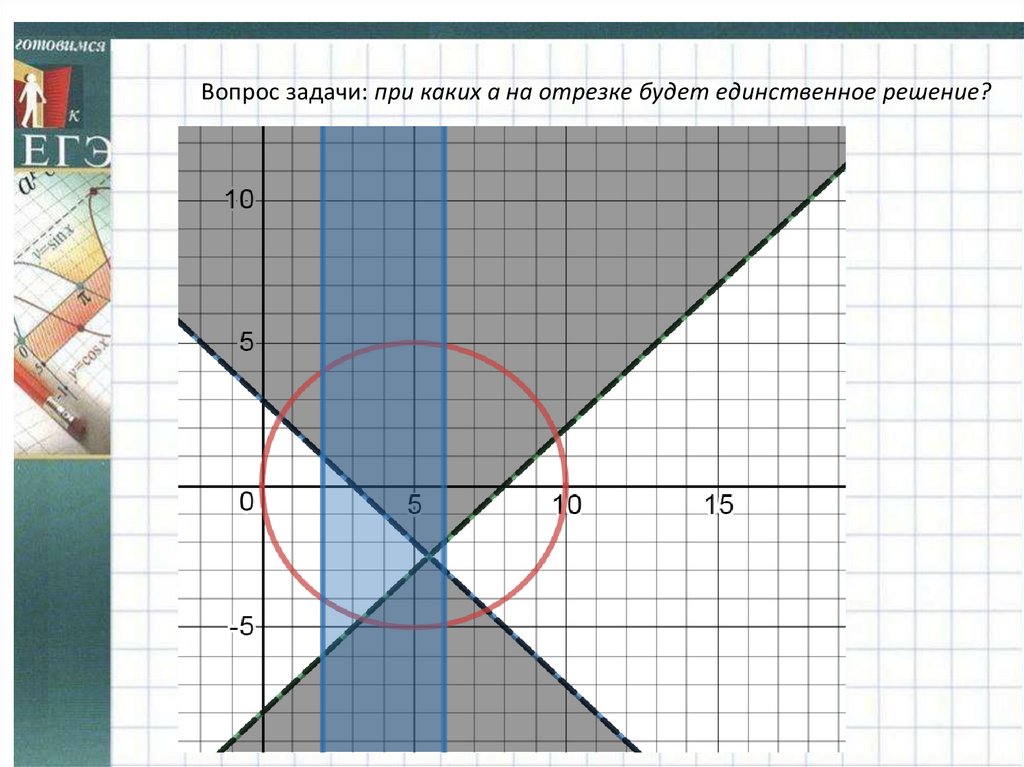
Вопрос задачи: при каких а на отрезке будет единственное решение?11.
ах
12.
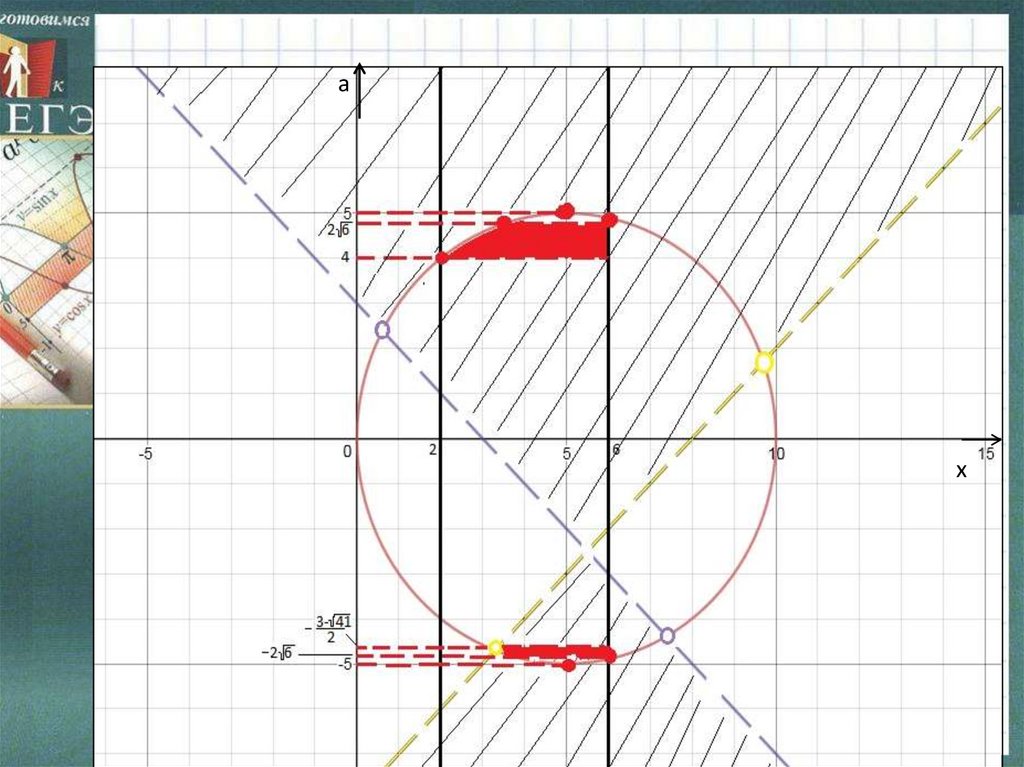
Нас интересует прежде всего а=-5. Это самая нижняя точка .Затем найдем ординату точки пересечения окружности и прямой
а=х-8.Нам нужен меньший корень уравнения
При х=6 получаем отрицательное а=
Одно решение будет получаться на данном отрезке еще,
если ординаты точек окружности будут больше или равны
ординаты точки пересечения окружности и прямой х=2, и меньше
или равны ординаты точки пересечения с прямой х=6.
Кроме того,а=5.
ОТВЕТ:
13.
ЗАДАЧА №3При каких a неравенство
не имеет решений на интервале (1;2)?
Решение::
14.
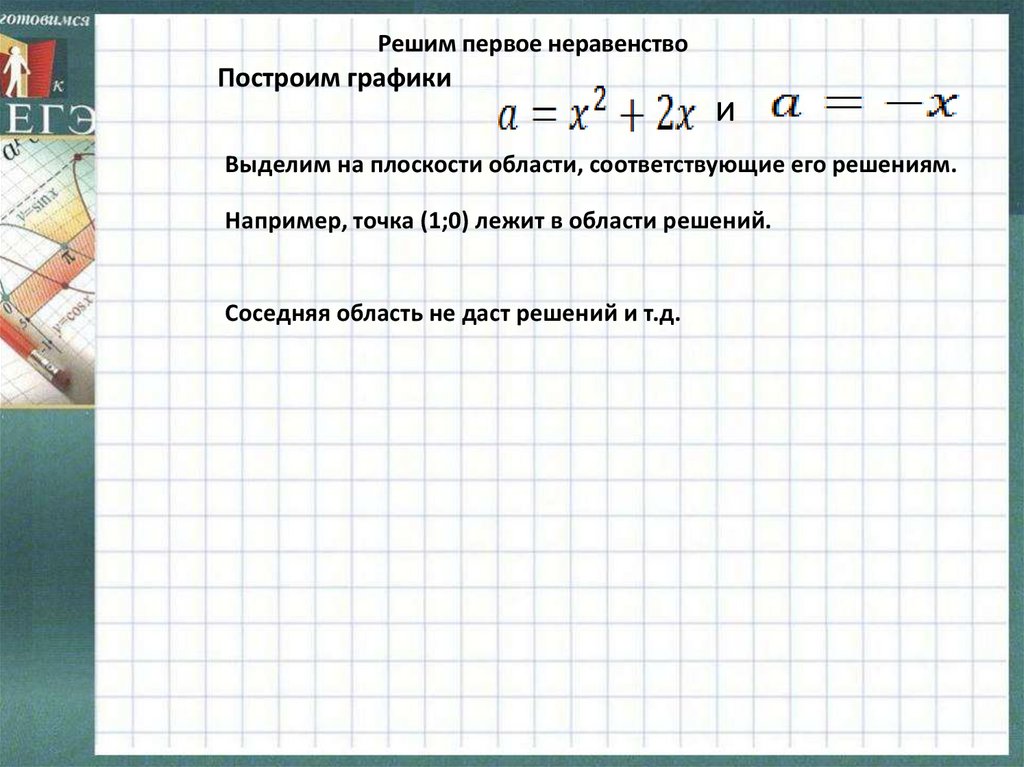
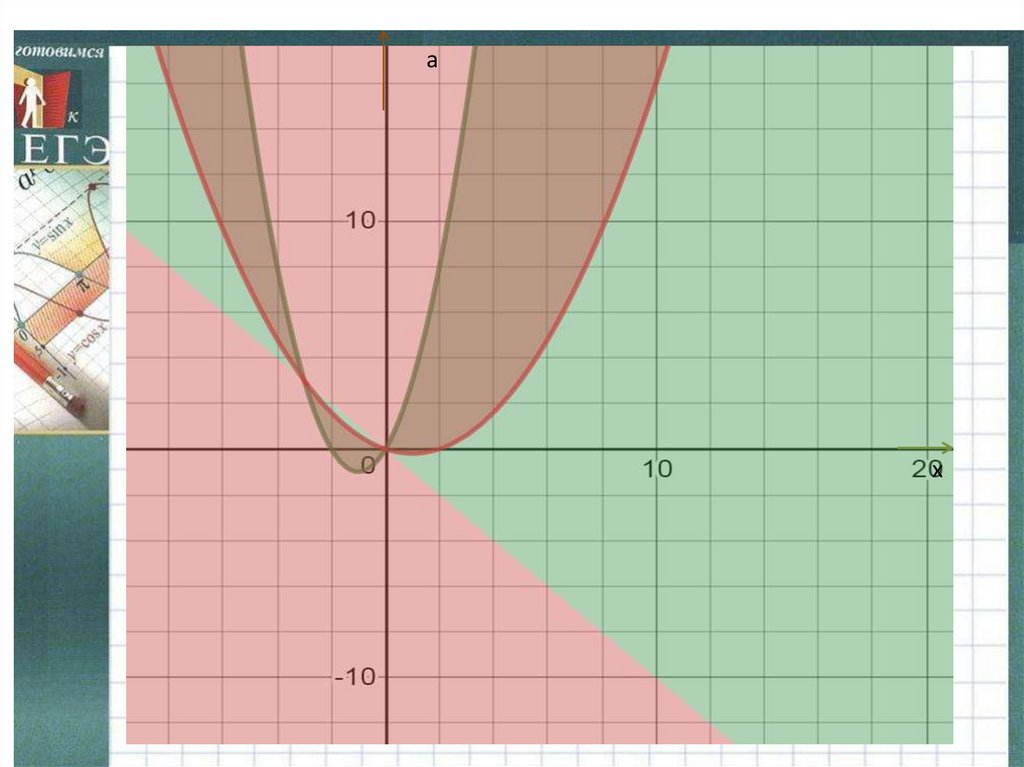
Решим первое неравенствоПостроим графики
и
Выделим на плоскости области, соответствующие его решениям.
Например, точка (1;0) лежит в области решений.
Соседняя область не даст решений и т.д.
15.
а-2
х
16.
Решим второе неравенство.Построим график
график
уже построен.Найдем область решений второго
неравенства
Найдем область решений системы неравенств
17.
ах
18.
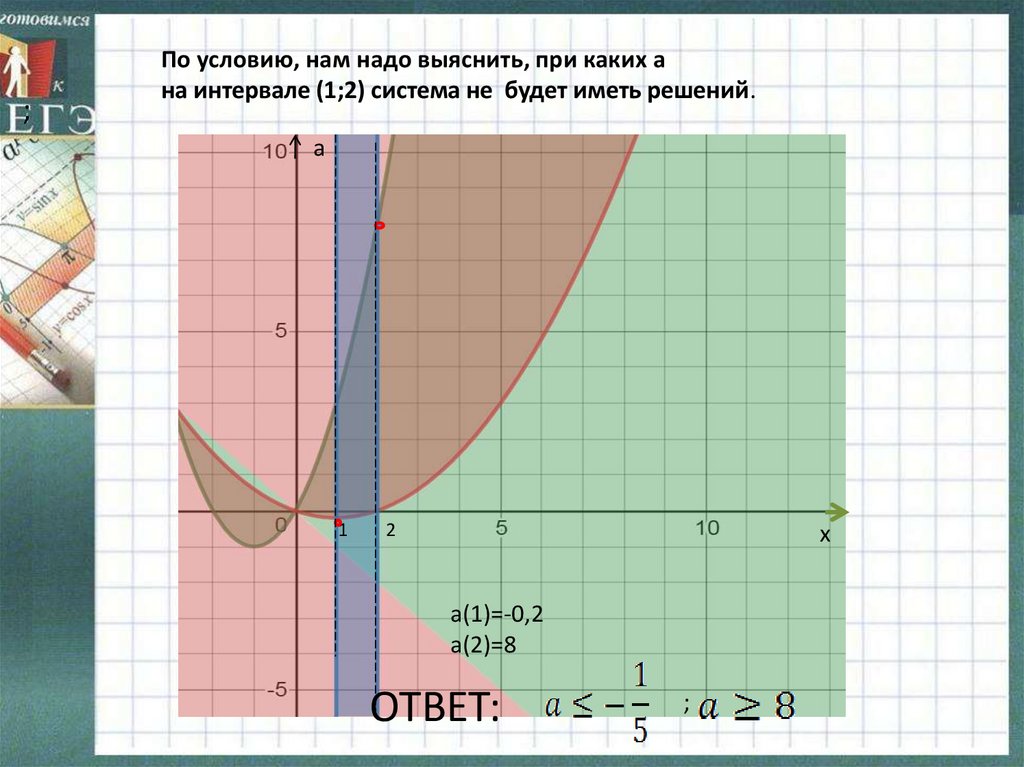
;По условию, нам надо выяснить, при каких а
на интервале (1;2) система не будет иметь решений.
а
1
2
х
а(1)=-0,2
а(2)=8
ОТВЕТ:
;









 mathematics
mathematics








