Метод динамического и электрофоретического светорассеяния

1.

Dinamic Light Scattering – DLS
Electrophoretic light scattering - ELS
Метод динамического и
электрофоретического
светорассеяния

2.

Оглавление
1. Задачи
2. Методы определения размеров частиц
3. Методы рассеяния света
4. Броуновское движение частиц
5. Принцип метода динамического рассеяния света
6. Математический аппарат метода
7. Ограничения метода
8. Распределение частиц по размерам. Примеры
9. Двойной электрический слой
10.Дзета-потенциал
11.Изоэлектрическая точка
12.Коагуляция
13.Электрофоретическое рассеяние света
14.Как измерить дзета-потенциал?
15.Метод электрофоретического светорассеивания [ELS]
16.Принципы работы анализаторов
17.Математические расчеты
18.Примеры
2

3.

Задачи
РФА позволяет определить размер частиц в сухих порошках.
Однако в наших системах НЧ находятся в водных растворах. Размер частиц в водных растворах другой – он больше, чем
в сухих образцах. Разница может быть в десятки раз.
Задача 1.
Как определить размер частиц в водных растворах или гидродинамический размер?
Задача 2.
Известно, что с НЧ в водных растворах происходит агрегация и седиментация. Как понять, устойчив наш раствор или
нет? Будут ли частицы осаждаться, или они стабильны?
Для этого надо узнать значение дзета-потенциала.
3

4.

Методы измерения
размеров
наночастиц
В сухих
порошках
В коллоидных
растворах
РФА
(область когерентного
рассеивания)
Динамическое
светорассеивани
е
СЭМ
(агрегаты)
4

5.

Дисперсная система
ДС – это гетерогенная система, состоящая из двух или более фаз с сильно развитой поверхностью
раздела между ними. Частицы дисперсной фазы имеют размеры от 1 нм до 10 мкм.
Примеры:
-аэрозоли (туманы, дымы, космическая пыль),
- золи металлов и природных минералов,
-донные отложения рек, морей и океанов, грунты и почвы, сырая нефть и природные битумы,
- пигменты и и высокодисперсные наполнители для лакокрасочных и композиционных материалов,
-керамические массы, цементы и бетонные смеси на их основе,
- мука и мучное тесто
- водноугольные суспензии и золы от сжигания твердых топлив
-водные суспензии целлюлозных волокон
-сырьевые шламы химических производств
ДС – дисперсная система, ДФ – дисперс(ион)ная фаза, ДЧ – дисперсная частица

6.

Какая общая физико-химическая основа для
изучения, описания и регулирования свойств ДС?
Общие фундаментальные физико-химические признаки для всех дисперсных
систем:
гетерогенность, то есть наличие поверхности раздела между фазами;
дисперсность (размер частиц, раздробленность)
На что влияют эти факторы?
Роль этих факторов существенна в проявлении свойств дисперсных систем:
агрегативной (А) и седиментационной (С) устойчивости (У) существенна по
мере увеличения дисперсности (уменьшения размера частиц) и их
концентрации в жидкой и дисперсных средах, т.е.
↑ дисперсность (↓ размер частиц) → ↑ АУ и ↑СУ
ДС – дисперсная система, ДФ – дисперс(ион)ная фаза, ДЧ – дисперсная частица

7.

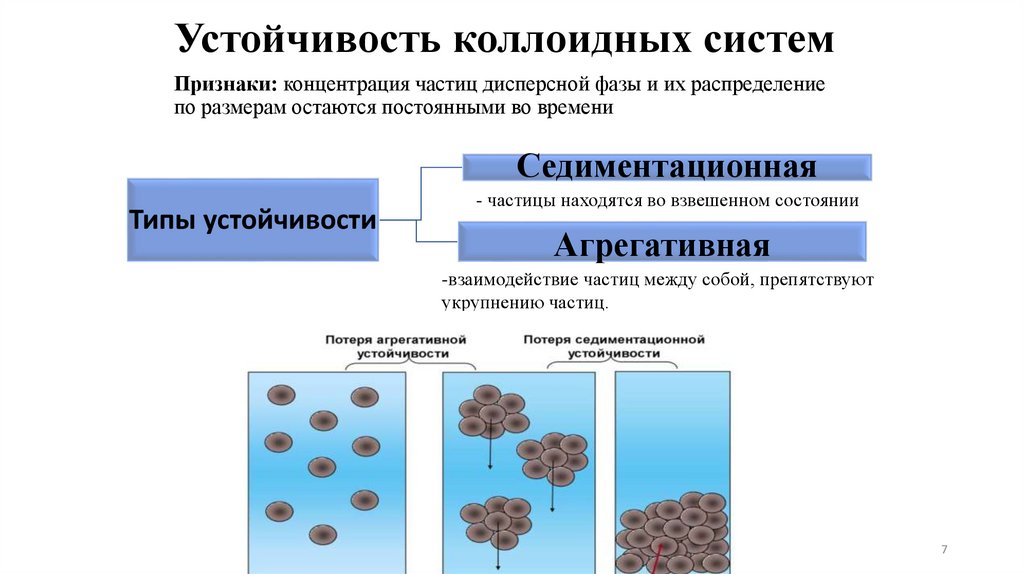
Устойчивость коллоидных систем
Признаки: концентрация частиц дисперсной фазы и их распределение
по размерам остаются постоянными во времени
Седиментационная
Типы устойчивости
- частицы находятся во взвешенном состоянии
Агрегативная
-взаимодействие частиц между собой, препятствуют
укрупнению частиц.
7

8.

Седиментационная устойчивость
- это способность дисперсной системы противостоять оседанию частиц.
Седиментация – оседание частиц под действием сил гравитации.
Из-за чего возникает седиментация?
Размер частиц [Чем больше размер частиц, тем больше сила тяжести]
Движение частиц [Для крупных частиц движение обеспечивается за счет сил
трения, для мелких частиц – тепловое движение]
Устойчивость обеспечивается:
1. Уменьшением силы тяжести (уменьшаем
размер частиц)
2. Увеличением вязкости среды
3. Увеличением температуры – ускорение
броуновского движения
8

9.

Агрегативная устойчивость
- это способность дисперсной системы сохранять во времени степень
дисперсности, т.е. размеры частиц и их индивидуальность, т.е. другими словами
способность системы противостоять укрупнению частиц.
Коагуляция – слипание, образование
агрегатов, их укрупнение и снижение
концентрации.
Из-за чего возникает коагуляция?
• изменение температуры;
• действие электрического и электромагнитного
полей;
• действие видимого света; облучение
элементарными частицами;
• механическое воздействие;
• добавление электролитов и др.
9

10.

Методы определения размеров частиц
Метод ситового анализа
Динамический анализ цифрового изображения
Седиментация
Центрифугирование
Микроскопия
По электропроводности
По затемнению света
Динамическое рассеяние света
Статическое рассеяние света
3
10

11.

Методы рассеяния света
• Динамическое рассеяние света (квазиупругое рассеяние
света, фотонная корреляционная спектроскопия, лазерная
корреляционная спектроскопия)
Позволяет определить: коэффициент диффузии, диаметр частиц
• Электрофоретическое рассеяние света
(электрофоретическая корреляционная спектроскопия)
Позволяет определить: дзета-потенциал, электрофоретическую
подвижность
11

12.

Броуновское движение частиц
Броуновское движение частиц – это беспорядочное движение
малых частиц, взвешенных в жидкости или газе, происходящее
под действием ударов молекул окружающей среды.
Причины
Броуновского
движения - тепловое движение
молекул среды и отсутствие
точной компенсации ударов,
испытываемых
частицей
со
стороны
окружающих
её
молекул,
т.е.
броуновское
движение
обусловлено
флуктуациями давления.
12

13.

13

14.

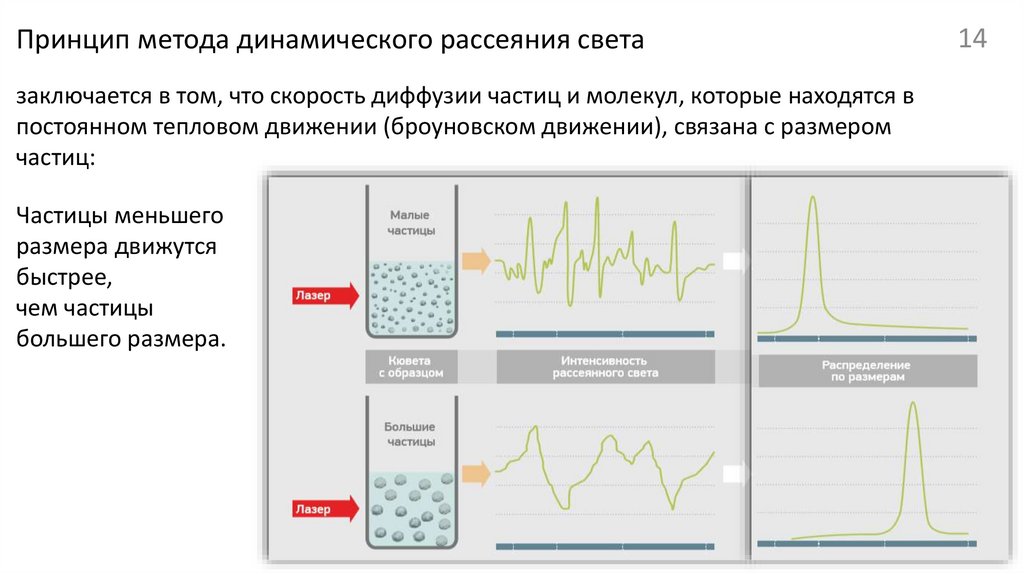
Принцип метода динамического рассеяния света
заключается в том, что скорость диффузии частиц и молекул, которые находятся в
постоянном тепловом движении (броуновском движении), связана с размером
частиц:
Частицы меньшего
размера движутся
быстрее,
чем частицы
большего размера.
14

15.

15

16.

16

17.

Математический аппарат метода
Такого рода флуктуирующие сигналы анализируются устройством,
называемым коррелятором, который строит автокорреляционную
функцию сигнала I(t).
1
=
Intensity
Correlation
Coefficient
g 2 ( ) I(t ) I(t )
0
Time
0
1
2
3
Time
17

18.

18

19.

Коэффициент диффузии D:
2
g 2 1 C Z D exp q D dD
Dmin
Dmax
2
Z(D) – функция распределения рассеивающих частиц по коэффициентам диффузии,
4 n
С – параметр, q sin 2 – волновой вектор рассеяния; kd – параметр, определяющийся
как термодинамическими, так и гидродинамическими взаимодействиями в растворе.
Коэффициент
диффузии
уравнение Эйнштейна-Стокса
kT
D0
6 Rh
Rh - гидродинамический радиус частицы;
- вязкость раствора;
Т – абсолютная температура;
k – постоянная Больцмана.
гидродинамический
радиус частицы
19

20.

Примеры автокорреляционных функций:
20

21.

Relative % in class
Распределение частиц по размерам
Примеры
Diameter, nm
Diameter, nm
Diameter, nm
21

22.

23.

Существует три распределения по размерам:
- Объемное
- Численное
- По интенсивности
A basic guide to particle characterization, whitepaper, Malvern Instruments Worldwide

24.

Частицы - это трехмерные объекты, и, если они не являются идеальными сферами (например,
эмульсиями или пузырьками), они не могут быть полностью описаны одним измерением,
таким как радиус или диаметр.
Чтобы упростить процесс измерения, часто удобно определять размер частиц, используя
концепцию эквивалентных сфер. В этом случае размер частицы определяется диаметром
эквивалентной сферы, имеющей те же свойства (например, объем или массу), что и
фактическая частица. Важно понимать, что разные методы измерения используют разные
модели эквивалентных сфер и, следовательно, не обязательно будут давать одинаковый
результат для частицы.
диаметр.
A basic guide to particle characterization, whitepaper, Malvern Instruments Worldwide
24

25.

Индекс полидисперсности: ИП -> 0
Монодисперсная система
Полидисперсная система
25

26.

Particle size distributions
Если образец, который вы хотите охарактеризовать, не является идеально монодисперсным, он будет состоять из
статистического распределения частиц разных размеров. Обычной практикой является представление этого
распределения в виде кривой распределения частот.
1. Числовое распределение характеризует долю частиц с разным размером в
общем количестве частиц («в штуках») в системе.
2. Распределения, взвешенные по объему: Вклад каждой частицы в
распределении пропорционален к объему этой частицы (эквивалент массе,
если плотность), то есть относительный пропорционален (размеру).
3. Распределения, взвешенные по интенсивности: частицы рассеивают свет
с разной интенсивностью
A basic guide to particle characterization, whitepaper, Malvern Instruments Worldwide
26

27.

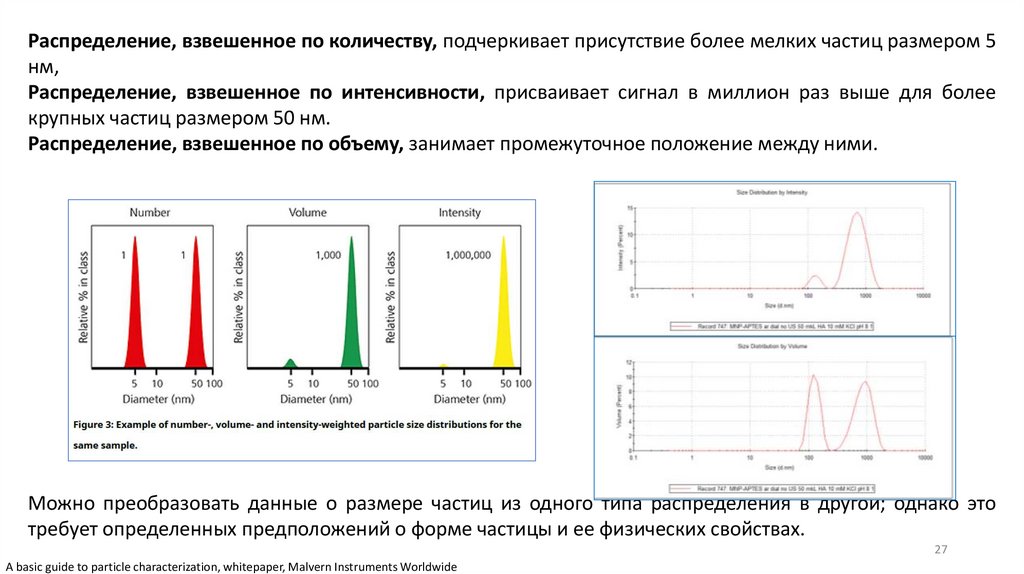
Распределение, взвешенное по количеству, подчеркивает присутствие более мелких частиц размером 5
нм,
Распределение, взвешенное по интенсивности, присваивает сигнал в миллион раз выше для более
крупных частиц размером 50 нм.
Распределение, взвешенное по объему, занимает промежуточное положение между ними.
Можно преобразовать данные о размере частиц из одного типа распределения в другой; однако это
требует определенных предположений о форме частицы и ее физических свойствах.
27
A basic guide to particle characterization, whitepaper, Malvern Instruments Worldwide

28.

It is important to note that dynamic light
scattering produces an intensity-weighted
particle size distribution, which means that the
presence of oversized particles can dominate
the particle size result.

29.

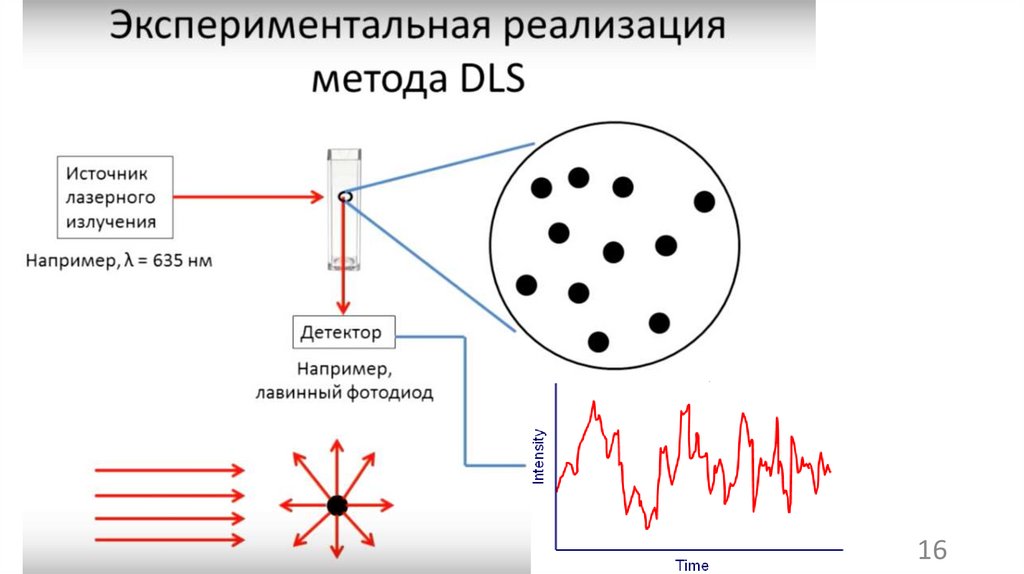
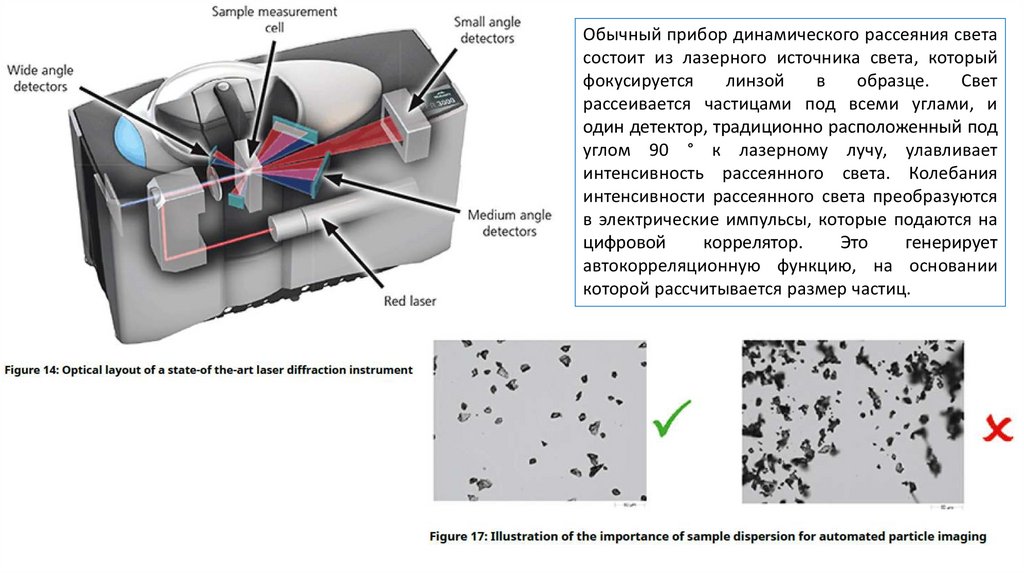
Обычный прибор динамического рассеяния света
состоит из лазерного источника света, который
фокусируется
линзой
в
образце.
Свет
рассеивается частицами под всеми углами, и
один детектор, традиционно расположенный под
углом 90 ° к лазерному лучу, улавливает
интенсивность рассеянного света. Колебания
интенсивности рассеянного света преобразуются
в электрические импульсы, которые подаются на
цифровой
коррелятор.
Это
генерирует
автокорреляционную функцию, на основании
которой рассчитывается размер частиц.
29

30.

Измерение дзета-потенциала
Метод электрофоретического светорассеивания
ELS
30

31.

Двойной электрический слой
Межфазный слой - совокупность двух поверхностных слоев при контакте фаз.
Двойной электрический слой (ДЭС) - разделение зарядов противоположного знака в межфазном слое. Возникает
при контакте двух фаз, из которых хотя бы одна – жидкость.
Потенциалоопределяющие ионы образуются на
поверхности частицы.
Противоионы притягиваются из жидкой фазы за счет
сил электростатического взаимодействия.
Слой противоионов состоит из:
-Адсорбционного слоя или слоя
Штерна
(ионы неподвижны)
-Диффузный слой или слой Гуи
(ионы подвижны).
31

32.

Дзета-потенциал
Плоскость скольжения разделяет подвижную внешнюю среду от
неподвижного граничного слоя (при движении частицы слой
разрывается).
Величина, характеризующая способность коллоидной частицы
двигаться в растворе электролита под действием внешнего
электрического поля, называется электрофоретической
подвижностью:
μ = v/ E
ζ-потенциал – потенциал на плоскости скольжения
– потенциал на поверхности коллоидной частицы
-разность потенциалов дисперсионной среды и
неподвижного слоя жидкости, окружающего частицу
-мера устойчивости коллоидной массы.
32

33.

Слой Штерна (плотный): внутренняя часть
адсорбированные дегидратированные ионы) +
внешняя часть (гидратированные ионы)
Плоскость скольжения разделяет подвижную
внешнюю среду от неподвижного граничного слоя
(при движении частицы слой разрывается. Место
разрыва – плоскость скольжения).
ζ-потенциал – потенциал на плоскости скольжения
– потенциал на поверхности коллоидной частицы
-разность потенциалов дисперсионной среды и
неподвижного слоя жидкости, окружающего частицу
-мера устойчивости коллоидной массы.

34.

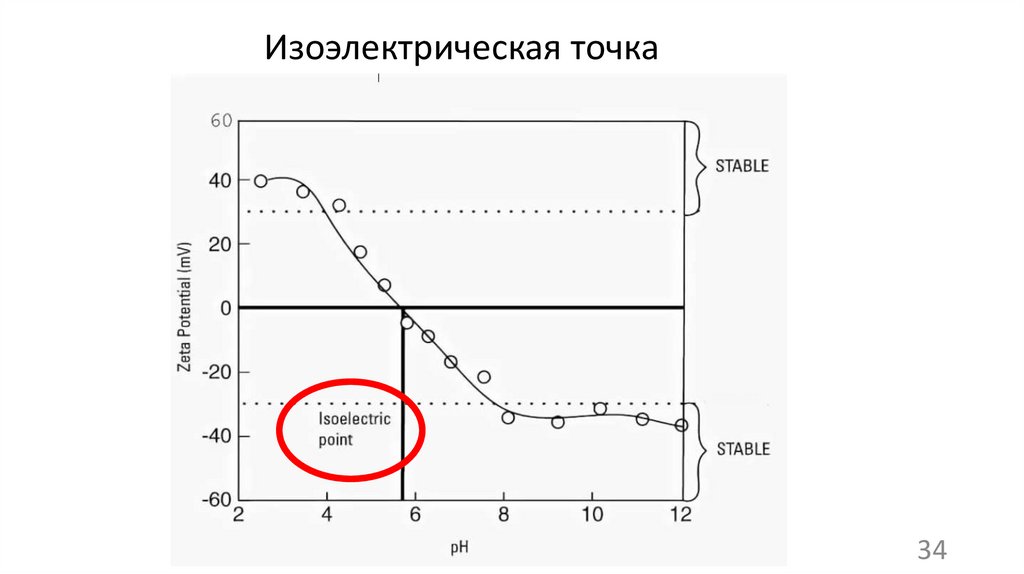
Изоэлектрическая точка
34

35.

Коагуляция
Fm – сила межмолекулярного
взаимодействия
Fэ –сила электростатического
отталкивания.
Если Fэ> Fm – устойчивость
Fэ< Fm – коагуляция.
Коагуляция происходит при
-избытке поверхностной энергии
- наличии на границе раздела фаз
реакционноспособных функциональных
групп.
Дзета-потенциал
Устойчивость коллоидной системы
От 0 до ± 30 мВ
Плохая устойчивость (возможна коагуляция)
Больше ± 30 мВ
Хорошая устойчивость
Зависимость притяжения и отталкивания от расстояния между частицами.
Зона I – притяжение
Зона II – отталкивание
λ=3,10,30 - толщина
диффузного слоя
35

36.

Электрофоретическое рассеяние света
Электрофорез — это электрокинетическое явление
перемещения частиц дисперсной фазы в жидкой или
газообразной
среде
под
действием
внешнего
электрического поля.
Скорость движения частиц зависит от:
• силы поля;
• диэлектрической постоянной среды;
• вязкости среды;
• дзета-потенциала
36

37.

Как измерить дзета-потенциал?
Измерение дзета-потенциала происходит по методу электрофоретического рассеяния света.
Для измерения дзета потенциала применяются специальные анализаторы,
позволяющие дополнительно проводить лабораторные измерения размера частиц.
В анализаторе дзета-потенциала измеряется скорость направленного движения
частиц в электрическом поле.
Для этого используется оптическая схема
лазерного доплеровского анемометра
(ЛДА) [измерения скоростей потоков
жидкости и газа]. Основное отличие этой
схемы состоит в наличии дополнительного
опорного луча, который позволяет измерить
доплеровскую скорость движения частиц.
37

38.

Метод электрофоретического
светорассеивания [ELS]
Электрическое поле в жидкости создается парой электродов,
погруженных в исследуемую дисперсную систем.
Принцип действия лазерного доплеровского анемометра
(ЛДА) заключается в следующем. Движущийся объект
облучают пучком лазерного излучения от неподвижного
источника. Это излучение отражается от объекта и
регистрируется неподвижным приемником. Вследствие
эффекта Доплера, частота излучения, попадающего на
приемник, будет отличаться от частоты излучения
неподвижного источника на некоторую величину,
пропорциональную скорости движения объекта относительно
источника и приемника.
Эффе́кт До́плера — изменение частоты и, соответственно,
длины волны излучения, воспринимаемое наблюдателем
(приёмником), вследствие движения источника излучения
и/или движения наблюдателя (приёмника).
38

39.

Принципы работы анализаторов
• DLS (dinamic light scattering). Цифровой коррелятор измеряет автокорреляционную
функцию затухания интенсивности рассеянного излучения.
• ELS (electrophoretic light scattering). Цифровой коррелятор измеряет
автокорреляционную функцию доплеровского сигнала. Программа обработки из
измеренной периодической функции находит доплеровскую частоту и, соответственно,
электрофоретическую скорость движения частиц.
Используется специальный метод анализа доплеровского сигнала - PALS (Phase analysis
light scattering). PALS процессор измеряет сдвиг фазы падающего лазерного луча при
рассеянии света, вызваном движением частиц.
39

40.

Математические расчеты с использованием
полученных экспериментальных данных
Скорость движения частиц в
поле, рассчитанная из
фазовой функции, позволяет
определить
электрофоретическую
подвижность частиц.
Электрофоретическая подвижность
частиц пересчитывается в дзетапотенциал с использованием теории
Смолуховского и применением
поправок для различной толщины
двойного электрического слоя.
v - скорость движения
заряженных частиц в
электрическом поле с
напряженностью E.
ζ – дзета-потенциал
μE - электрофоретическая подвижность
ε – диэлектрическая проницаемость
η – вязкость
40

41.

41

42.

42

43.

43

44.

Зачем нужен гидродинамический
диаметр?
- Наночастицы, в том числе модифицированного магнетита, могут
быть использованы в медицинских целях, где попадая в жидкости
организма, они будут иметь размер, отличный от размера в сухом
порошке. Встает вопрос соотношения гидродинамического
диаметра и диаметра участков кровеносной системы.
44

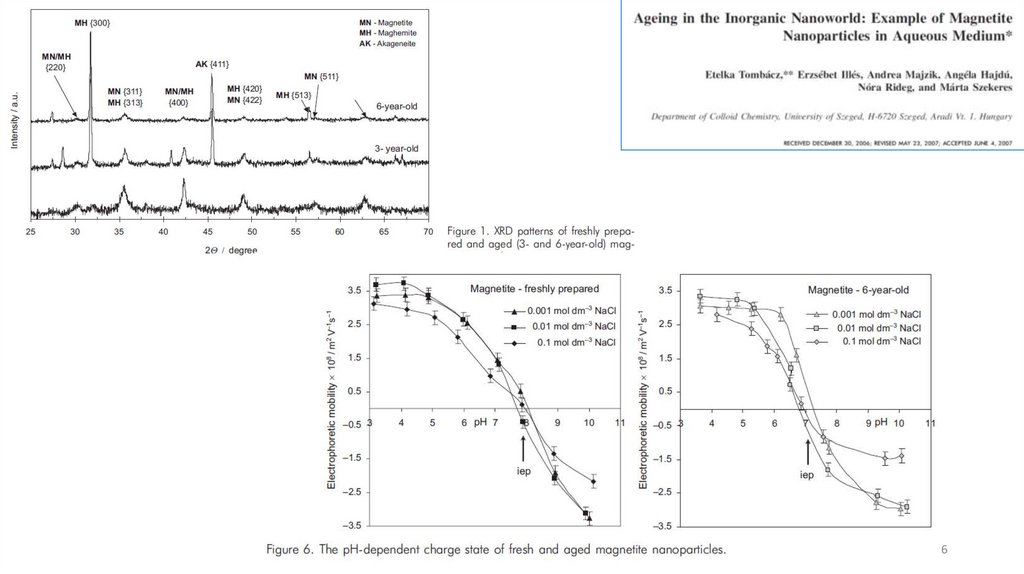
45.

Зачем нужна изоэлектрическая точка?
• Положение изоэлектрической точки позволяет идентифицировать
наночастицы. Например, из литературы известно положение
изоэлектрической точки для магнетита и маггемита.
• Позволяет оценить степень покрытия поверхности.
pH ИЭТ = 3.5
pH ИЭТ = 6.5
pH ИЭТ = 10.5
Gorbani, 2019
Wang, 2009
Bini, 2014
45

46.

46

47.

47

48.

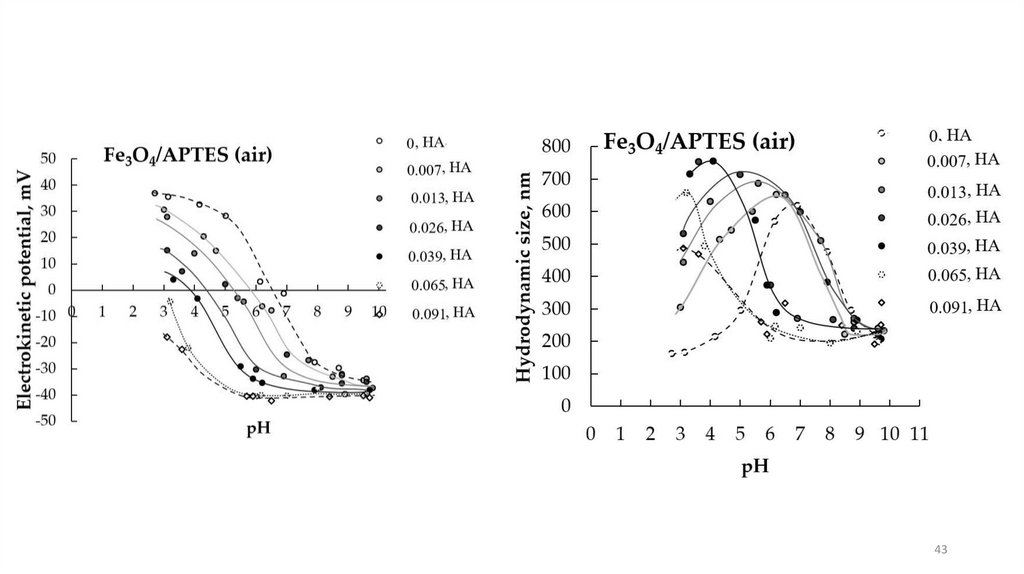
ВЛИЯНИЕ АДСОРБЦИИ ГК на дзета-потенциалы наночастиц
Fe3O4/АПТЭС при изменении рН
Fe3O4-АПТЭС (II)
Fe3O4
50
Дзета-потенциал, мВ
0,1
30
20
00mkL HA
0.0258
50
mkl HA
10
0
-10 1
3
5
7
9 pH
150
mkL HA
0.0387
-30
0.0645
250
mkL HA
-40
450
mkL HA
0.1161
-60
0,08
0,06
0.0283
110
mkL HA
-20
-50
Fe3O4-АПТЭС (I-D-Us)
ГК, г/г
Fe3O4/АПТЭС (I-D-M)
40
Fe3O4-АПТЭС (I-D-M)
Fe3O4-АПТЭС (I)
17
0,04
0,02
0
Fe3O4
Fe3O4
Fe3O4-APTES
Fe3O4-APTES
Fe3O4-APTES
Fe3O4-APTES
Fe3O4/
Fe3O4/
Fe3O4/
Fe3O4/
(I)
(I-D-US)
(II)
(I-D-M)
АПТЭС
(I-D-M)
АПТЭС (I)
АПТЭС (I-D-Us) АПТЭС (II)
Влияние адсорбции ГК (г/г) на поверхностный заряд НЧ при различных
рН (KCl = 0,01 М, Malvern Zetasizer NanoZS, Университет Сегеда)
Концентрация ГК, необходимая для полного покрытия 1 г НЧ (ξ ~ -20 мВ, pH=3)
Добавление ГК приводит к перезарядке поверхности наночастиц в кислой области с ~+40 на ~-40 мВ.
Дзета-потенциал наночастиц Fe3O4/АПТЭС позволяет оценить сорбционную емкость по отношению к ГК и выявить
корреляцию «поверхностный заряд- сорбционная емкость».

49.

АГРЕГАТИВНАЯ УСТОЙЧИВОСТЬ НАНОЧАСТИЦ Fe3O4/AПТЭС-ГК
40
Дзета-потенциал, мВ
30
Fe3O4-APTES
Fe3O4/АПТЭС(I-D-M)
(I-D-M)
20
ГК, г
10
0
-10 0
0,02
0,04
0,06
0,08
0,1
Fe3O4-APTES
Fe3O4/АПТЭС(I-D-Us)
(I-D-Us)
Fe3O4/АПТЭС (I)
Fe3O4-APTES
(I)
-20
-30
Fe3O4-APTES
(II)
Fe3O4/АПТЭС (II)
-40
Fe3O4
Fe3O4
-50
0
Fe3O4
Fe3O4
Fe3O4/АПТЭС (II)
Fe3O4-APTES(II)
Fe
Fe3O4-APTES(I-D-Us)
3O4/АПТЭС (I-D-Us)
Fe3O4/АПТЭС (I-D-M)
Fe3O4-APTES(I-D-M)
Fe3O4-APTES(I)
Fe3O4/АПТЭС (I)
Влияние ГК на заряд наночастиц и коллоидную стабильность
дисперсий (рН ~ 5, KCl = 0,01 М).
Концентрация ГК, необходимая для изменения ξ, г/г
СГК, г
Fe3O4
Fe3O4/
АПТЭС (II)
Fe3O4/
АПТЭС (I)
Fe3O4/АПТЭС
(I-D-Us)
Fe3O4/АПТЭС
(I-D-M)
ИЭТ
0.008
0.006
0.004
0.01
0.025
ξ=-20мВ
0.016
0.038
0.014
0.018
0.038
ξ=плато
0.04
0.056
0.04
0.028
0.072
0,005
0,01
0,015
0,02
0,025
0,03
0,035
0,04
ГК, г/г
Интервалы концентрации ГК (г/г), при которых система не стабильна
(pH∼5, КCl = 0.01 M, 20мВ≤ ξ ≤-20 мВ)
Концентрация адсорбированных ГК варьируется для каждого образца
Fe3O4/АПТЭС.
Адсорбционная емкость образцов НЧ по отношению к ГК значительно
превышает точку компенсации электростатического заряда (ξ=0 мВ), что
указывает на дополнительный вклад различных типов связыванеия ГК с
НЧ помимо NH2-групп.
Образец Fe3O4/АПТЭС (I-D-M) сохраняет стабильность даже при низких
концентрациях ГК вследствие исходного большего значения ξ-потенциала.

50.

Исследуемые параметры и приборы
Гидродинамический размер, нм
Дзета потенциал, мВ, ξ
Коэффициент полидисперсности
Шприцы для титрования HCL и KOH
pH 3-10
Электрод
УЗ-ванна
NanoZS apparatus (Malvern, UK)
Zetasizer software 711
750 измерений

51.

Distribution statistics
"There are three kinds of lies: lies, damned lies, and
statistics."
Twain/Disraeli
In order to simplify the interpretation of particle size distribution data, a range of statistical parameters can be calculated and
reported. The choice of the most appropriate statistical parameter for any given sample will depend upon how that data will
be used and with what it will be compared. For example, if you wanted to report the most common particle size in your
sample you could choose between the following parameters:
• mean - 'average' size of a population (средняя
арифметическая величина)
• median - size in the middle of a frequency distribution
(Это значение размера частиц, которое разделяет
популяцию распределения точно на две равные
части, т.е. точка на кривой где 50% распределения
находятся слева от этой точки, а 50% - справа. )
• mode - size with highest frequency (наивысшая
точка кривой
распределения.)
51
A basic guide to particle characterization, whitepaper, Malvern Instruments Worldwide

52.

Means
There are many different means that can be defined, depending upon how the distribution data are collected
and analyzed. The three most commonly used for particle sizing are described below.
1. Number length mean D[1,0] or Xnl
The number length mean, often referred to as the arithmetic mean, is most important when the number of
particles is of interest, e.g. in particle counting applications. It can only be calculated if we know the total
number of particles in the sample, and is therefore limited to particle counting applications.
2. Surface area moment mean D[3, 2] or Xsv
The surface area mean (Sauter Mean Diameter) is most relevant when the specific surface area is important
e.g. bioavailability, reactivity, dissolution. It is most sensitive to the presence of fine particulates in the size
distribution.
3. Volume moment mean D[4, 3] or Xvm
The volume moment mean (De Brouckere Mean Diameter) is relevant for many samples as it reflects the
size of those particles which constitute the bulk of the sample volume. It is most sensitive to the presence
of large particulates in the size distribution
52

53.

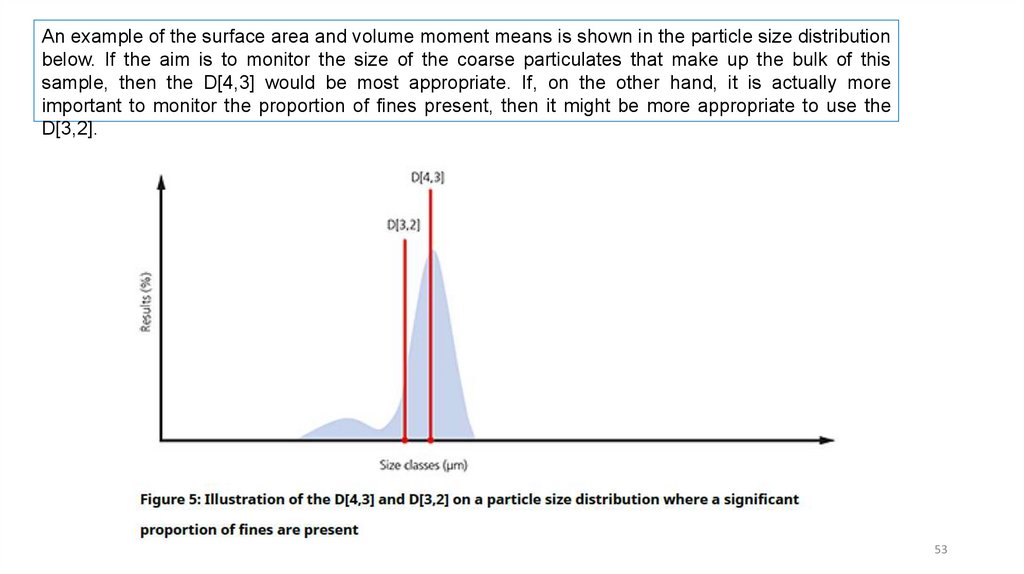
An example of the surface area and volume moment means is shown in the particle size distribution
below. If the aim is to monitor the size of the coarse particulates that make up the bulk of this
sample, then the D[4,3] would be most appropriate. If, on the other hand, it is actually more
important to monitor the proportion of fines present, then it might be more appropriate to use the
D[3,2].
53