Similar presentations:
Операции со множествами. Практическая работа №1
1.
Практическаяработа №1
ОПЕРАЦИИ СО
МНОЖЕСТВАМИ
2.
Фронтальный опросКем были заложены основы логики,
науки о законах и формах
человеческого мышления?
Что изучает математическая логика?
В чем суть формализация знаний и
рассуждений? (приведите пример)
Что изучает дискретная математика?
Что такое множество?
Какие операции над множествами вы
знаете и в чем их суть?
Что такое диаграммы Эйлера -Венна?
3.
Пушкин17 30 48
140 10 01
126 138
140 3 501
Маяковский
2 46 38 1
116 14 20!
15 14 21
14 0 17
4.
Есенин14 126 14
132 17 43.
16 42... 511
704 83.
170! 16 39
514 700 142
612 349
17 114 02
5.
Частушки117 117
19 9 5!
117 117
48 35!
6.
Объединением (суммой)множеств А и В называется
множество А ∪ В,
элементы которого
принадлежат хотя бы
одному из этих множеств.
Например, если
А={1,2,4}, B={3,4,5,6}, то
А ∪ B = {1,2,3,4,5,6}
7.
Пересечением(произведением) множеств А
и В называется множество А
∩ В, элементы которого
принадлежат как множеству
А, так и множеству В.
Например, если А={1,2,4},
B={3,4,5,2}, то А ∩ В = {2,4}
8.
Разностью множеств А и Вназывается множество АВ,
элементы которого
принадлежат множесву А,
но не принадлежат
множеству В.
Например, если
А={1,2,3,4}, B={3,4,5}, то
А\В = {1,2}
9.
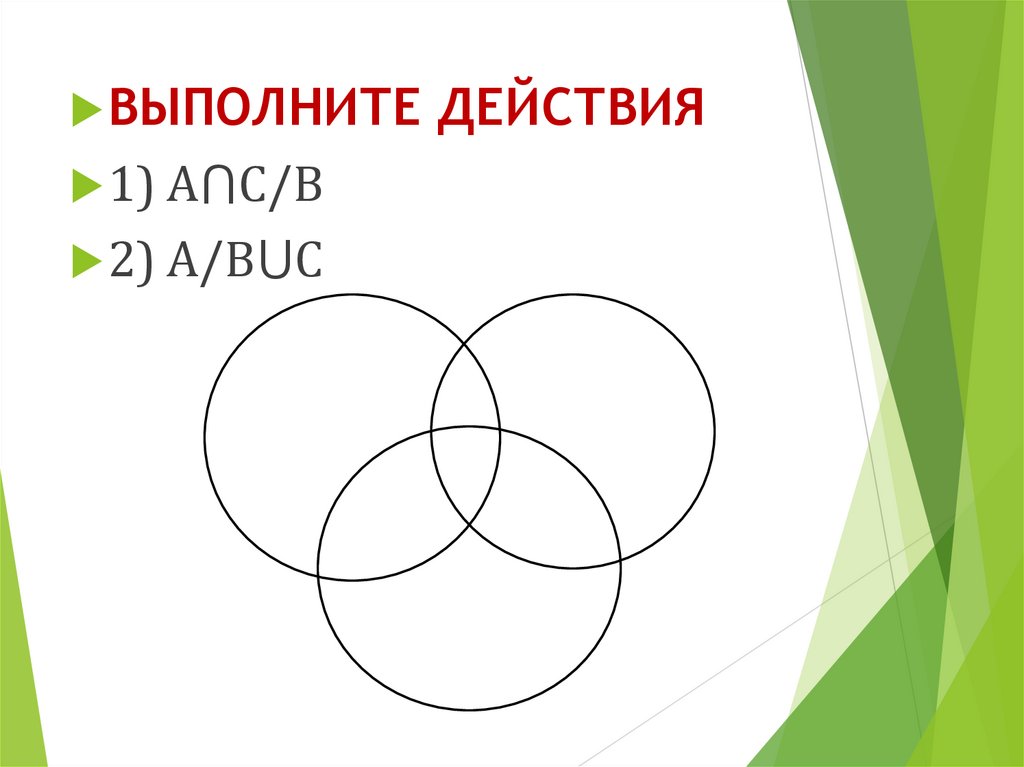
ВЫПОЛНИТЕ ДЕЙСТВИЯ1) А⋂С/В
2) А/В⋃С
10.
Найдите объединение,пересечение, разность и универсум
множеств
А={1,3,4,0,6,2,4},
B={2, 1,4,3,6,3}
11.
Решите задачу графическиДано:
а) A, B ⊆ Z,
A = {1;2;5;7;9;11}, B = {1;4;6;7}.
б) A, B ⊆ R, A = [4; 7), B = [3; 6].
Найти: A ∩ B, A ∪ B, A\B, B\A.
12.
Задача №1В группе 30 человек, каждый из которых поет или
танцует. Известно, что поют 17 человек, а танцевать
умеют 19 человек. Сколько человек поет и танцует
одновременно?
13.
Задача №2Каждая семья, живущая в нашем доме,
выписывает или газету, или журнал, или и
то и другое вместе. 75 семей выписывает
газету, а 27 семей выписывают журнал и
лишь 13 семей выписывают и журнал, и
газету. Сколько семей живет в нашем доме?
14.
Задача №3На занятии по литературе преподаватель решил узнать, кто из
40 студентов 2 –го курса читал книги А, В, С. Результаты
опроса выглядели так: книгу А прочитали 25 студентов, книгу
В – 22 студента, книгу С – 22 студента; одну из книг А или В
прочитали 33 человека, одну из книг А или С прочитали 32
человека, одну из книг В или С – 31 человек. Все три книги
прочитали 10 студентов. Сколько студентов: а) прочитали
только по одной книге; б) прочитали ровно две книги; в) не
прочли ни одной из указанных книг
15.
ВЫПОЛНЕНИЕПРАКТИЧЕСКОЙ
РАБОТЫ.
Задания для
самостоятельной работы














 mathematics
mathematics








