Осевая симметрия. 6 класс

1.

Урок – мастерская
в 6 классе
по теме Осевая симметрия
Автор: учитель математики высшей
квалификационной категории
Колесникова Татьяна Павловна

2.

Симметрия
Я в листочке, я в кристалле,
Я в живописи, архитектуре,
Я в геометрии, я в человеке.
Одним я нравлюсь, другие
Находят меня скучной.
Но все признают, что
Я – элемент красоты.
Симметрия! Я гимн тебе пою!
Тебя повсюду я в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза.

3.

Математика владеет не
только истиной, но и
высшей красотой –
красотой отточенной и
строгой, возвышенно
чистой и стремящейся к
подлинному совершенству,
которое свойственно лишь
величайшим образцам
искусства.
Бертран Рассел

4.

“Симметрия является той идеей,
посредством которой человек на
протяжении веков пытался постичь
и создать порядок, красоту и
совершенство”.
Г. Вейль

5.

Творчество людей во всех своих проявлениях
тяготеет к симметрии. Действительно,
симметричные объекты окружают нас со всех
сторон, мы имеем дело с симметрией везде.
Посредством симметрии человек пытался, по
словам немецкого математика Германа Вейля,
«постичь и создать порядок, красоту и
совершенство».
Герман Вейль

6.

Это же имел в виду и французский
архитектор Ле Карбюзье, когда
писал, что «человеку необходим
порядок; без него все действия
теряют согласованность,
логическую взаимосвязь…».
Получается, что симметрия – это
уравновешенность,
упорядоченность, красота,
совершенство.
Ле Карбюзье

7.

Симметрия
Симметрия в переводе с греческого«summetria» соразмерность,
пропорциональность, наличие
определенного порядка в
расположении частей.

8.

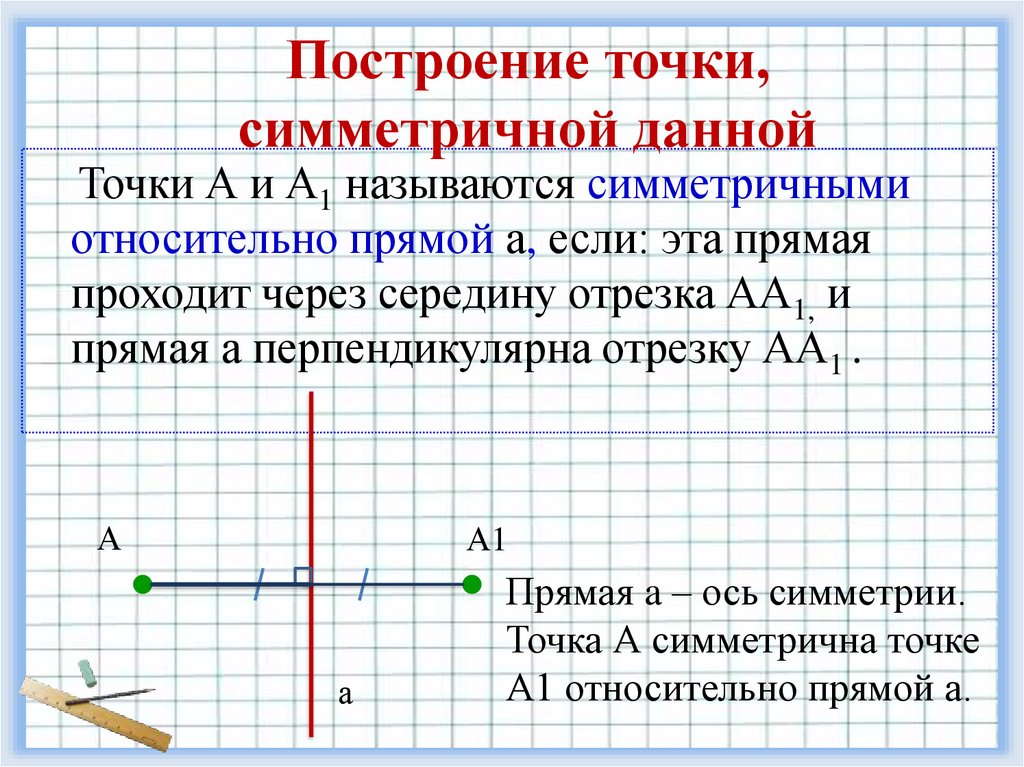
Построение точки,
симметричной данной
Точки А и А1 называются симметричными
относительно прямой а, если: эта прямая
проходит через середину отрезка АА1, и
прямая а перпендикулярна отрезку АА1 .
А
А1
а
Прямая a – ось симметрии.
Точка А симметрична точке
А1 относительно прямой а.

9.

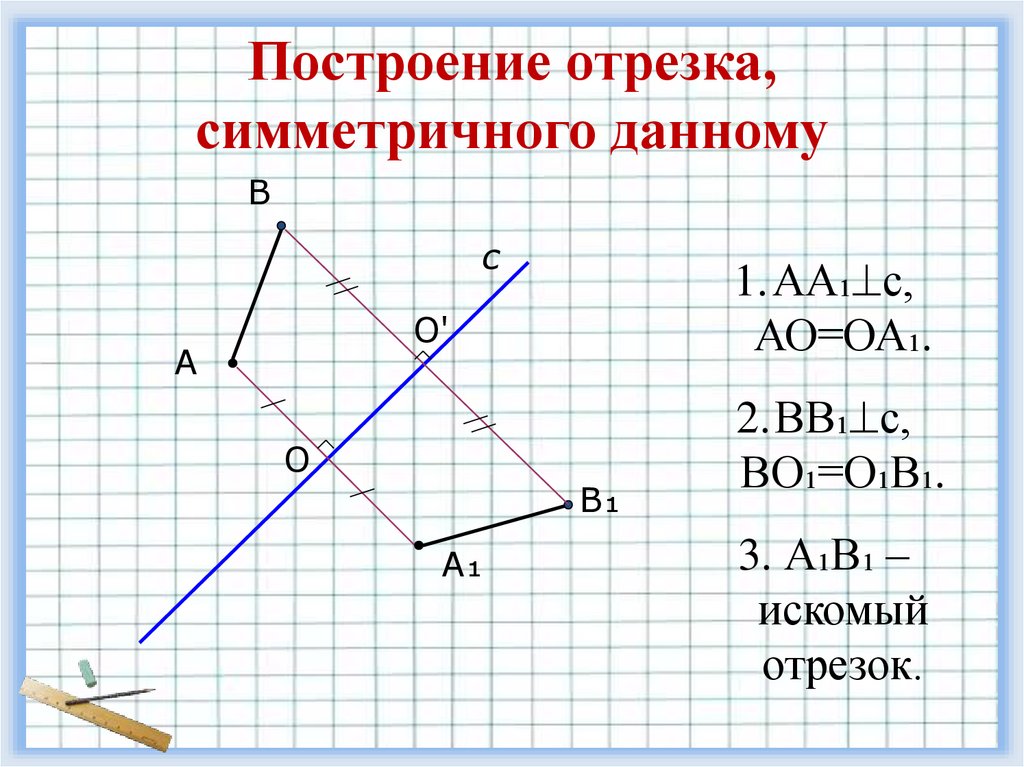
Построение отрезка,
симметричного данному
В
с
1.АА₁ с,
АО=ОА₁.
O'
А
O
В₁
А₁
2.ВВ₁ с,
ВО₁=О₁В₁.
3. А₁В₁ –
искомый
отрезок.

10.

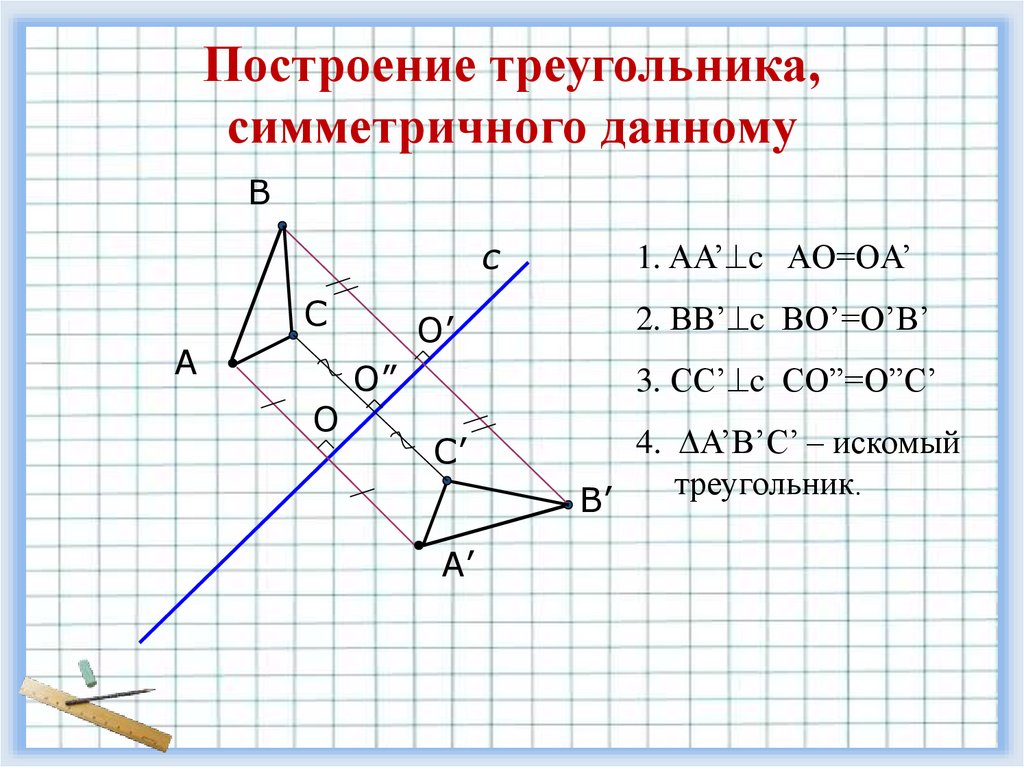
Построение треугольника,
симметричного данному
В
с
С
А
O
1. AA’ c AO=OA’
2. BB’ c BO’=O’B’
O’
O”
3. СС’ c СO”=O”С’
С’
В’
А’
4. A’B’С’ – искомый
треугольник.

11.

12.

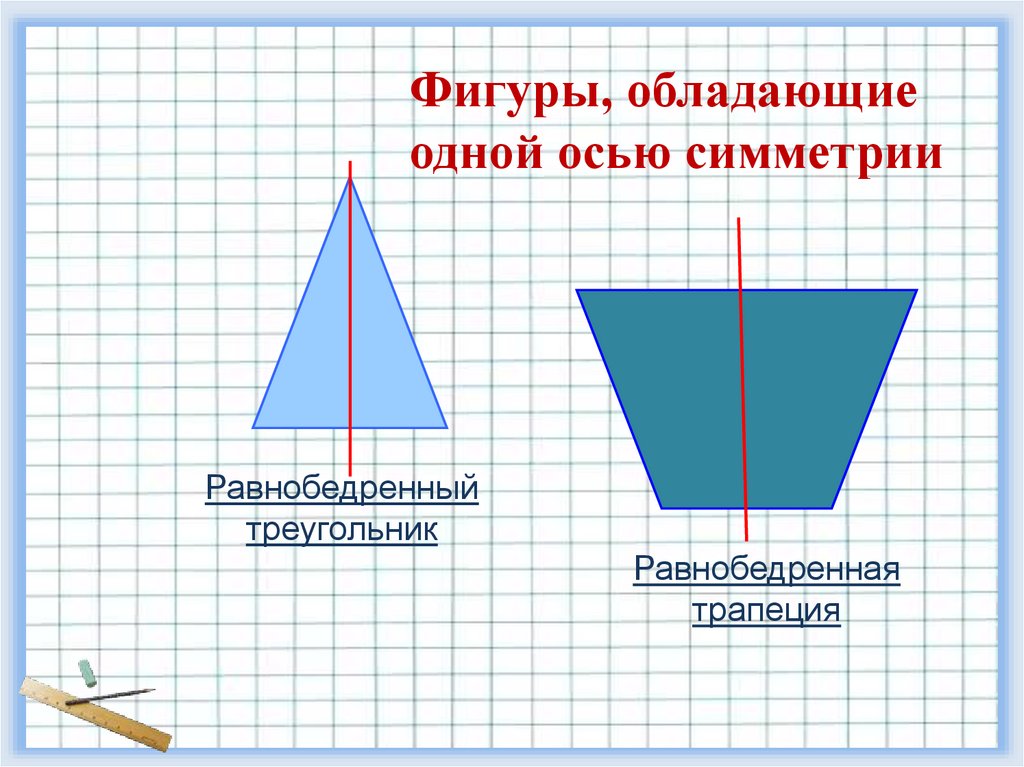
Фигуры, обладающие
одной осью симметрии
Равнобедренный
треугольник
Равнобедренная
трапеция

13.

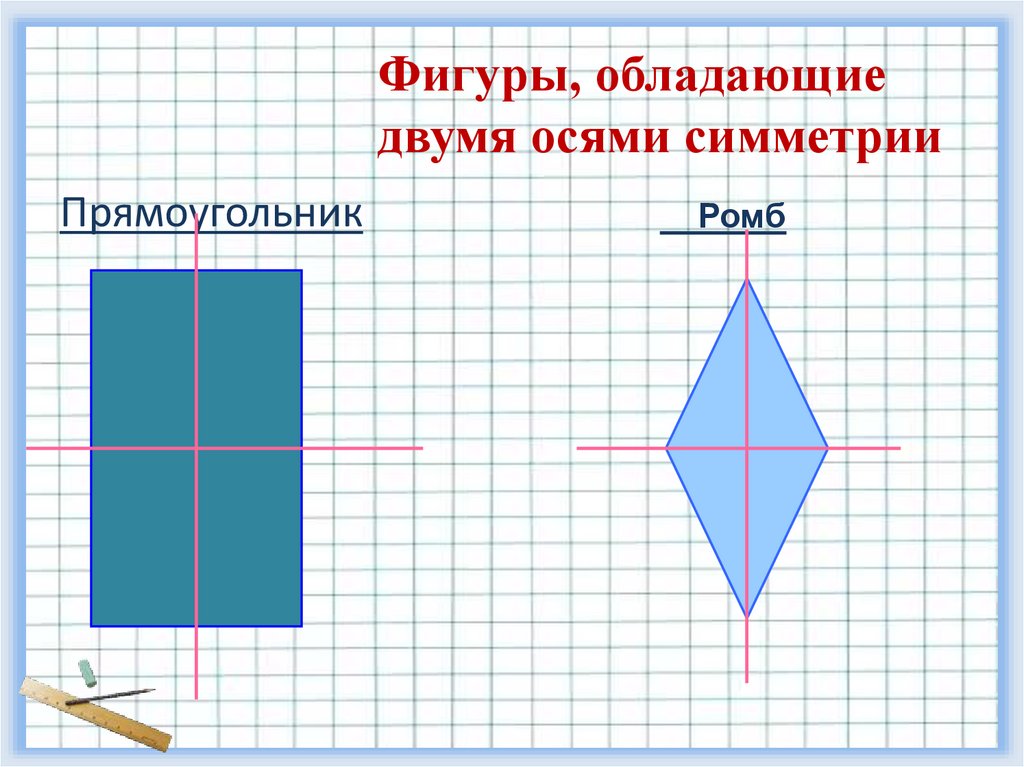
Фигуры, обладающие
двумя осями симметрии
Прямоугольник
Ромб

14.

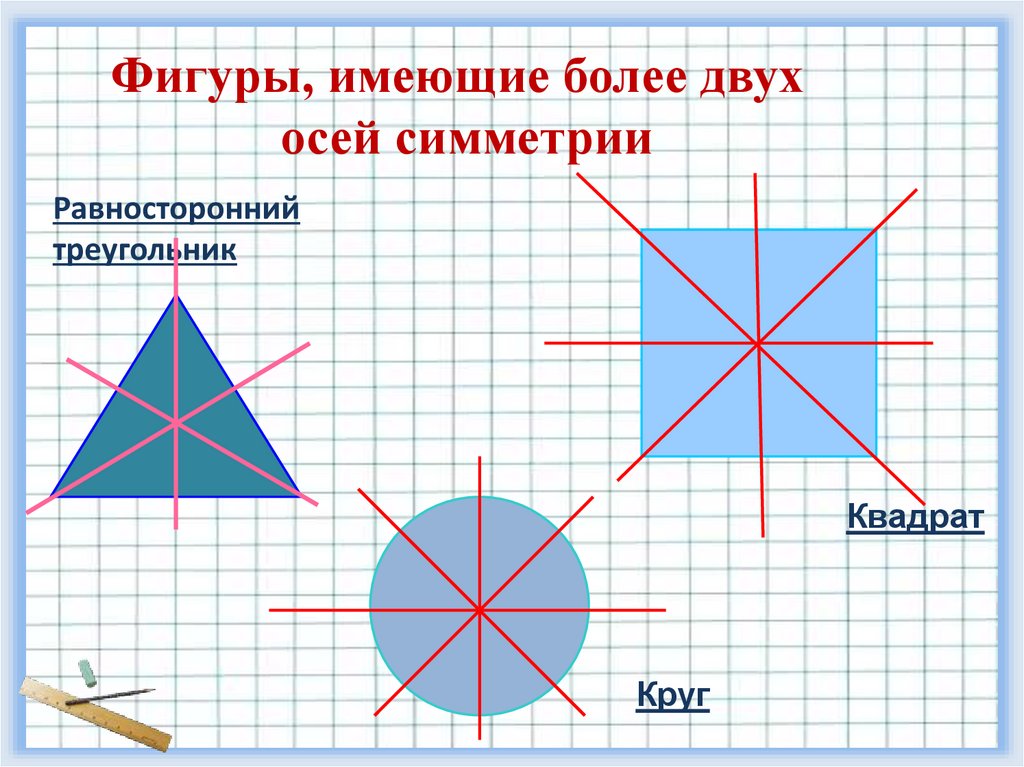
Фигуры, имеющие более двух
осей симметрии
Равносторонний
треугольник
Квадрат
Круг

15.

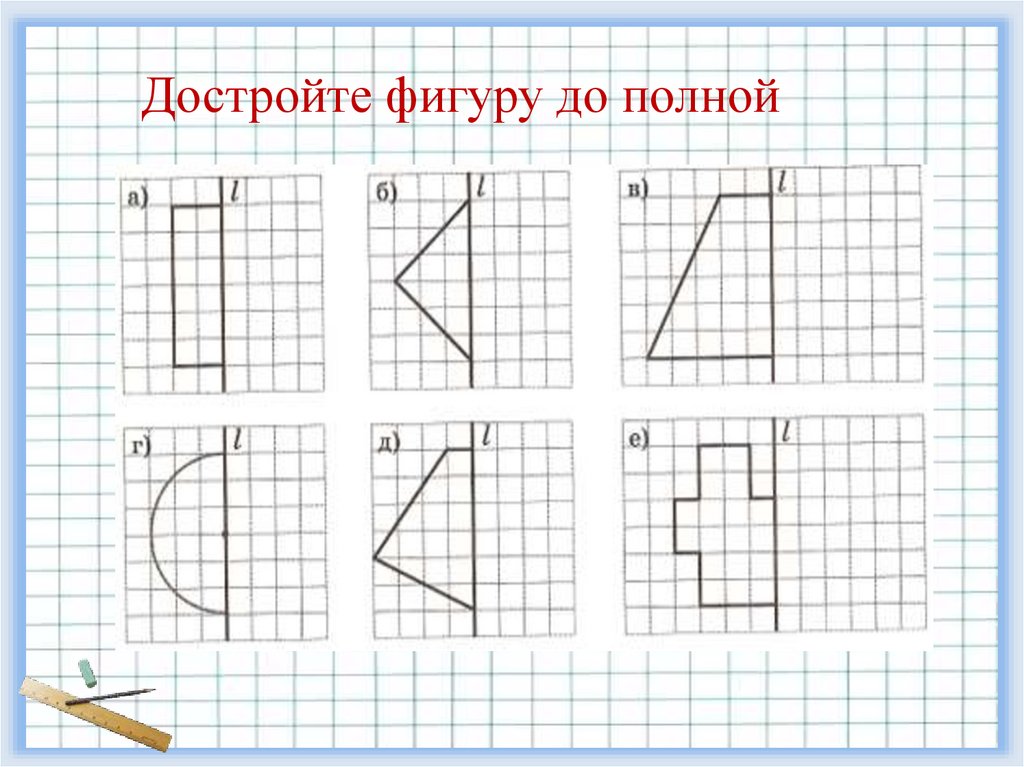
Достройте фигуру до полной

16.

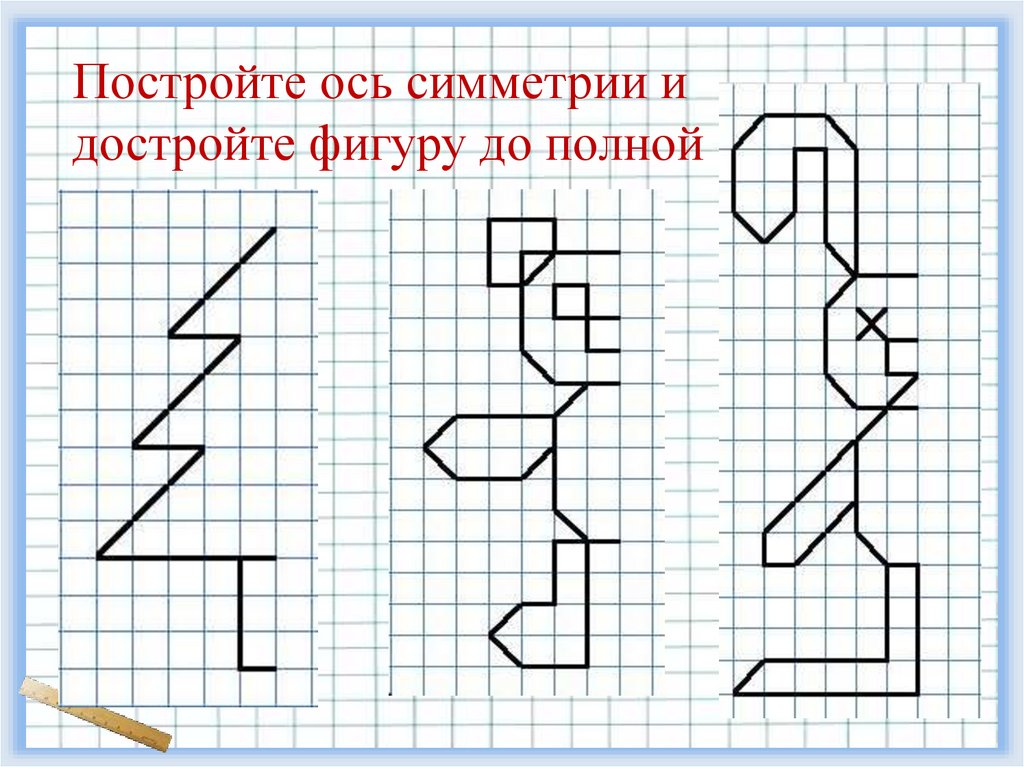
Постройте ось симметрии и
достройте фигуру до полной

17.

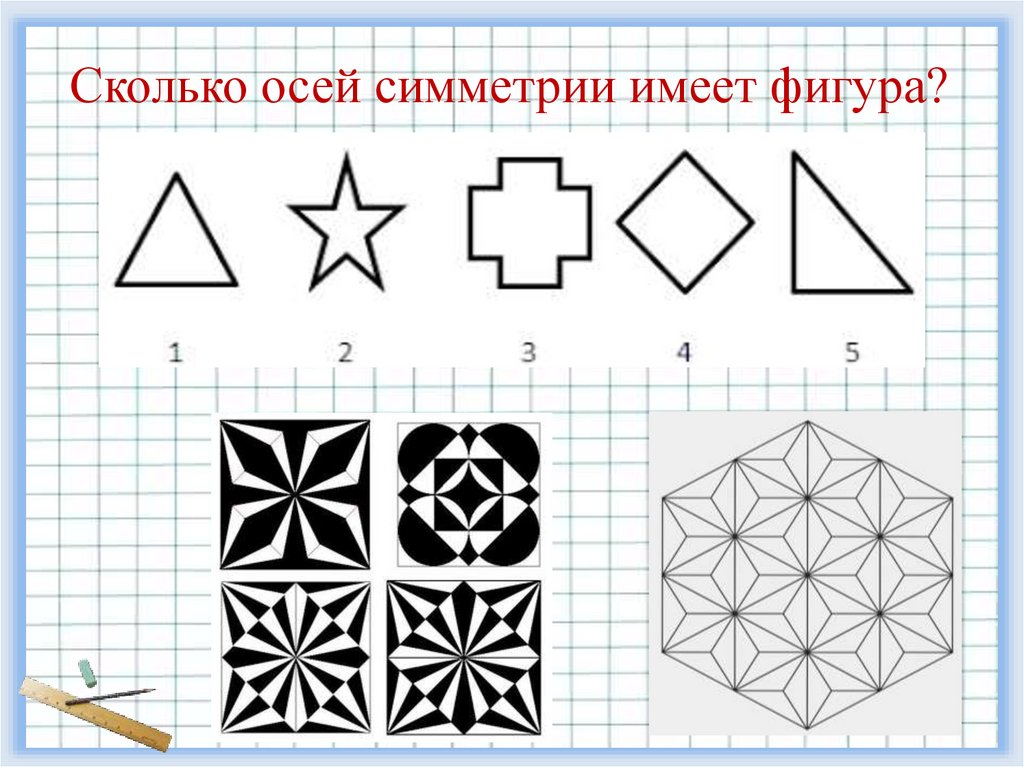
Сколько осей симметрии имеет фигура?

18.

Имеют ли буквы русского алфавита
ось симметрии?
Одна ось симметрии
А
В
Х
ЭО
ГЗТЕЮ
Р
Н
М
К
Б
И
Ж
Ф
Л
С
Д
УП
Две оси симметрии

19.

Домашнее задание
П. 7.1, стр. 144-148.
№№ 563,570,578, 586, 587

20.

Использованные материалы
https://images.app.goo.gl/1mQfy1Etao77QYdY7
https://images.app.goo.gl/W3dmkovZjqXMireX8
https://images.app.goo.gl/hNevdCZ3VjZwK1Ad7
https://images.app.goo.gl/L1fWrawJZ77oE2Xb9
https://images.app.goo.gl/Wk7cv8eaexZdiU959
https://images.app.goo.gl/MMerpaV6sgC8VfE59
https://images.app.goo.gl/kvoyeapYVn59apf39
https://images.app.goo.gl/b4rSFu5BDFr8DC1Q7
https://images.app.goo.gl/EnNkR6Ze8zy25CWX6
https://images.app.goo.gl/D5iJ91ag8LHAmW3V8
https://images.app.goo.gl/8hf9tkzty1Bq163p6