Similar presentations:
Формулы приведения
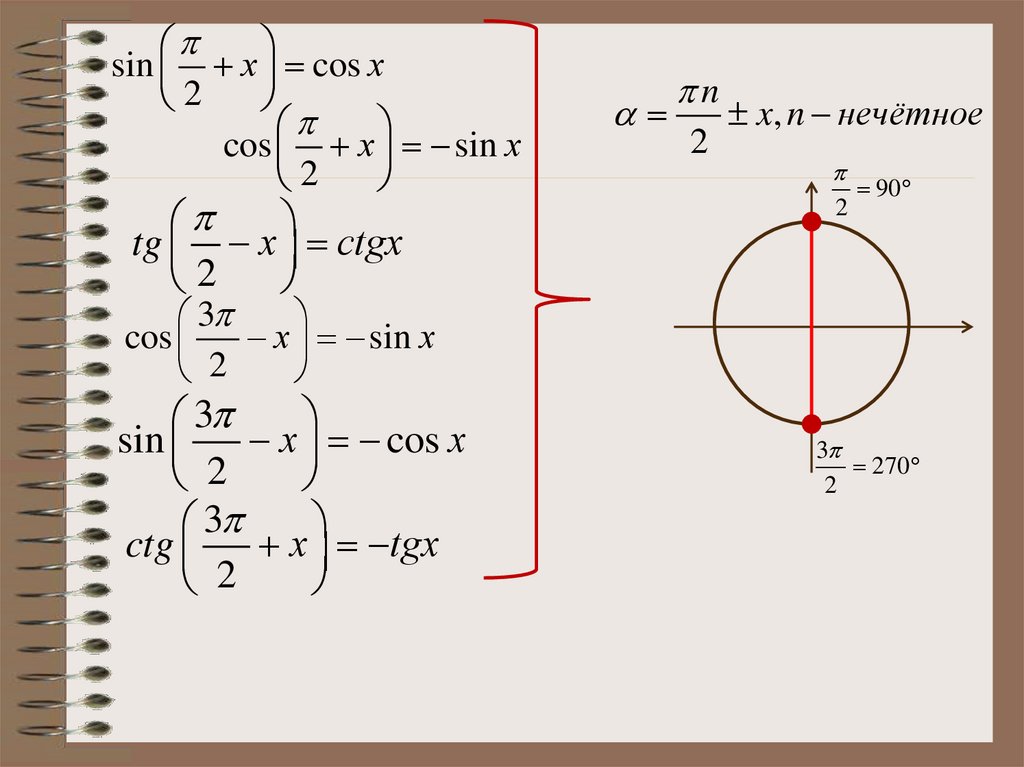
1. ФОРМУЛЫ ПРИВЕДЕНИЯ
12. знаки тригонометрических функций по четвертям
sin+ +
- - tg ; ctg
-+
+-
cos
-+
-+
2
3.
sin х sin хcos х cos х
ctg х ctgх
ctg х ctgх
tg 2 х tgх
tg 2 х tgх
sin 3 х sin х
cos 3 х cos х
n x
180
0
4.
sin х cos х2
cos х sin х
2
tg х ctgх
2
3
n
2
x, n нечётное
2
90
cos
х sin х
2
3
sin
х cos х
2
3
ctg
х tgх
2
3
270
2
5. ФОРМУЛЫ ПРИВЕДЕНИЯ ПРАВИЛО
• 1) Если под тригонометрической функцией0 2
аргумент равен x; 2 x , то название
функции не меняется.
2
3
2
• 2) Если под тригонометрической функцией
3
x;
x , то название
аргумент равен
2
2
функции меняется (на родственное).
• 3) Перед полученной функцией ставят знак, который
имела бы в данной четверти исходная функция при
условии, что х - угол 1 четверти.
5
6.
67.
78. Упростить выражение. Пример 1
3sin х cos х tg
x ctg 2 x
2
2
=
cos x sin 3 x
2
cos x cos x ctgx ctgx
=
0
sin x sin x
2
2
3
2
8
9.
Пример 2:3
2 sin 7 cos
2
Упростите :
sin
=
2sin sin
sin
1
9
10.
Пример 3:5cos 29
Вычислите :
sin 61
5cos 29
5cos 29
5
Решение :
sin 90 29 cos 29
5cos 90 61 5sin 61
Решение :
5
sin 61
sin 61
10
11.
Пример 4:3cos 54
Вычислите :
cos126
3cos 54
3cos54
3
Решение :
cos 180 54 cos 54
11
12.
Пример 5: Вычислите :12
sin 2 37 sin 2 127
12
Решение : 2
2
sin 37 sin 90 37
12
12
2
2
sin 37 cos 37
12











 mathematics
mathematics








