Логика - наука о мышлении

1.

Выполнила: ученица 6 класса
МБОУ СОШ №13 им.К.Хетагурова
Цаболова Дзерасса

2.

Логика – наука о
мышлении.

3. Введение

Увлечение математикой часто начинается с
размышлений над какой-то особенно
понравившейся задачей. Она может встретиться
и на школьном уроке, и на занятии
математического кружка, и в журнале или
книжке. А меня очень заинтересовали
логические задачи, с которыми я столкнулись на
уроке математики. И я решила узнать о них
больше.

4. Цель:

Знакомство с разными видами логических задач,
алгоритмами и методами их решения.

5.

Задачи исследования
Изучить
литературу с целью ознакомления с
разными видами логических задач, методами их
решения.
Научиться применять данные методы к решению
разного вида логических задач.
Подобрать логические задачи, решаемые
определёнными методами

6.

Предмет исследования
–
разнообразие методов решения логических задач.
Объект
исследования
– логические
задачи.
Методы
теоретический
анализ
синтез
сравнение
исследования:

7.

Методы решения логических задач:
Метод рассуждений
Метод таблиц
Метод графов
Метод кругов Эйлера
Комбинированный метод

8. Метод рассуждений

Примеры
Лена, Оля, Таня участвовали в беге на 100 м. Лена
прибежала на 2 с раньше Оли, Оля прибежала на
1 с позже Тани. Кто прибежал раньше: Таня или
Лена и на сколько секунд?

9.

Решение
Составим схему:
Лена
__________
Оля
__________ __ __
1с 1с
Таня
__________ __
1с
Ответ: раньше на 1с пришла Лена.

10. Метод таблиц Примеры В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. « Замечательно, что один

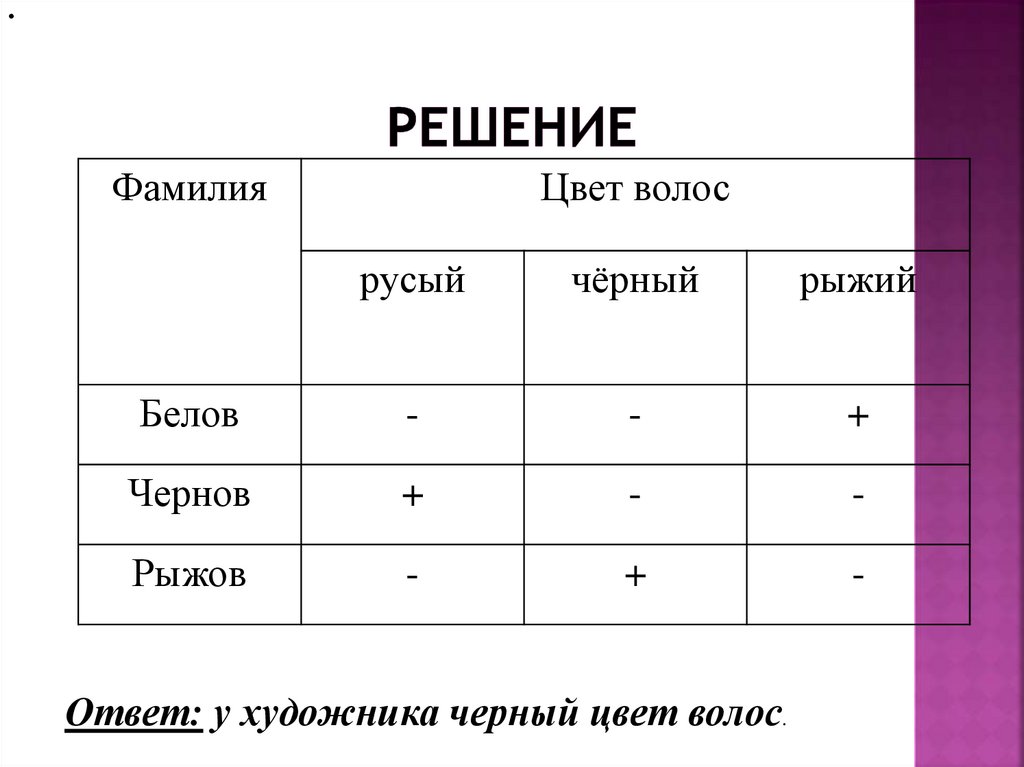
11. Решение

Фамилия
Цвет волос
русый
чёрный
рыжий
Белов
-
-
+
Чернов
+
-
-
Рыжов
-
+
-
Ответ: у художника черный цвет волос.

12. Метод графов

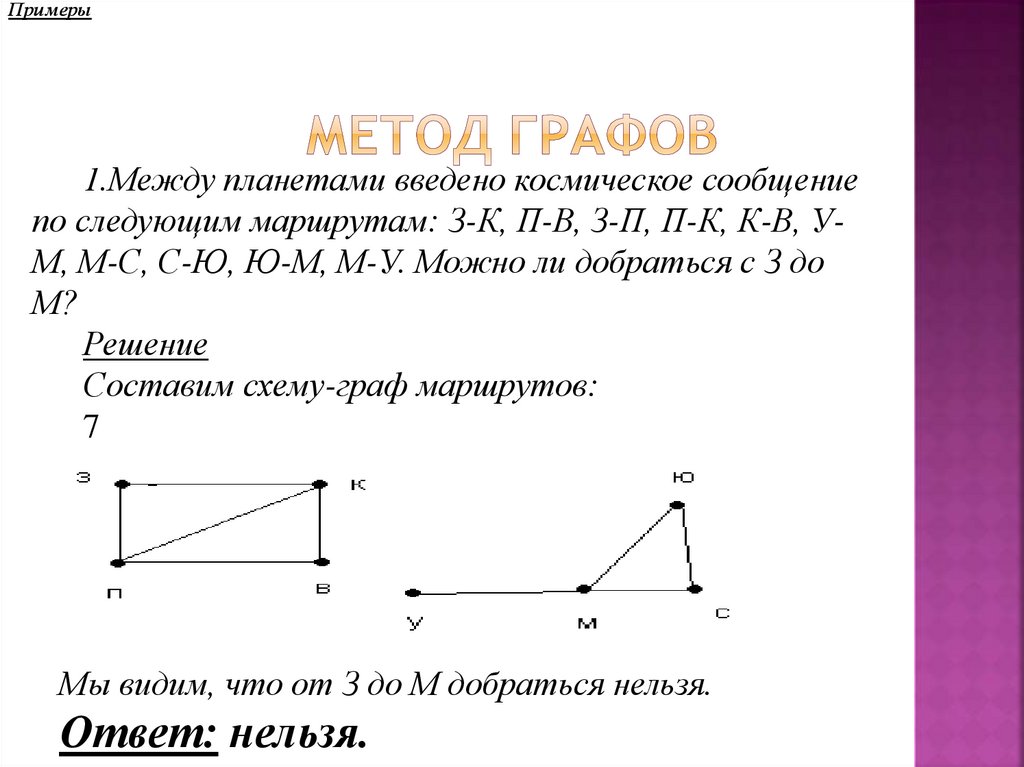
Примеры
1.Между планетами введено космическое сообщение
по следующим маршрутам: З-К, П-В, З-П, П-К, К-В, УМ, М-С, С-Ю, Ю-М, М-У. Можно ли добраться с З до
М?
Решение
Составим схему-граф маршрутов:
7
Мы видим, что от З до М добраться нельзя.
Ответ: нельзя.

13.

2. Аркадий, Борис. Владимир, Григорий и Дмитрий при
встрече обменялись рукопожатиями (каждый пожал руку
каждому по одному разу). Сколько всего рукопожатий было
сделано?
Решение
Пусть каждому из пяти молодых людей
соответствует
определенная
точка
на
плоскости, названная первой буквой его имени, а
производимому рукопожатию — отрезок или
часть кривой, соединяющая конкретные точки —
имена.

14. Решение

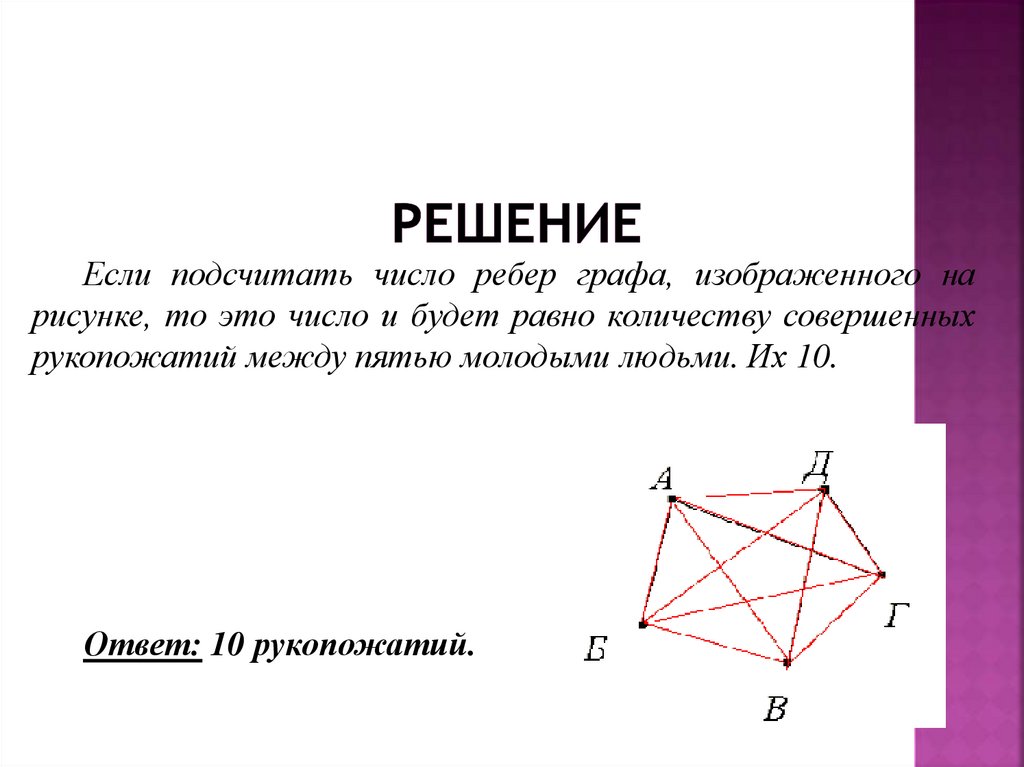
Если подсчитать число ребер графа, изображенного на
рисунке, то это число и будет равно количеству совершенных
рукопожатий между пятью молодыми людьми. Их 10.
Ответ: 10 рукопожатий.

15. Метод кругов Эйлера

Примеры
•Некоторые ребята из нашего класса любят ходить в кино.
Известно, что 15 ребят смотрели фильм «Обитаемый
остров», 11 человек – фильм «Стиляги», из них 6 смотрели и
«Обитаемый остров», и «Стиляги». Сколько человек
смотрели только фильм «Стиляги»?

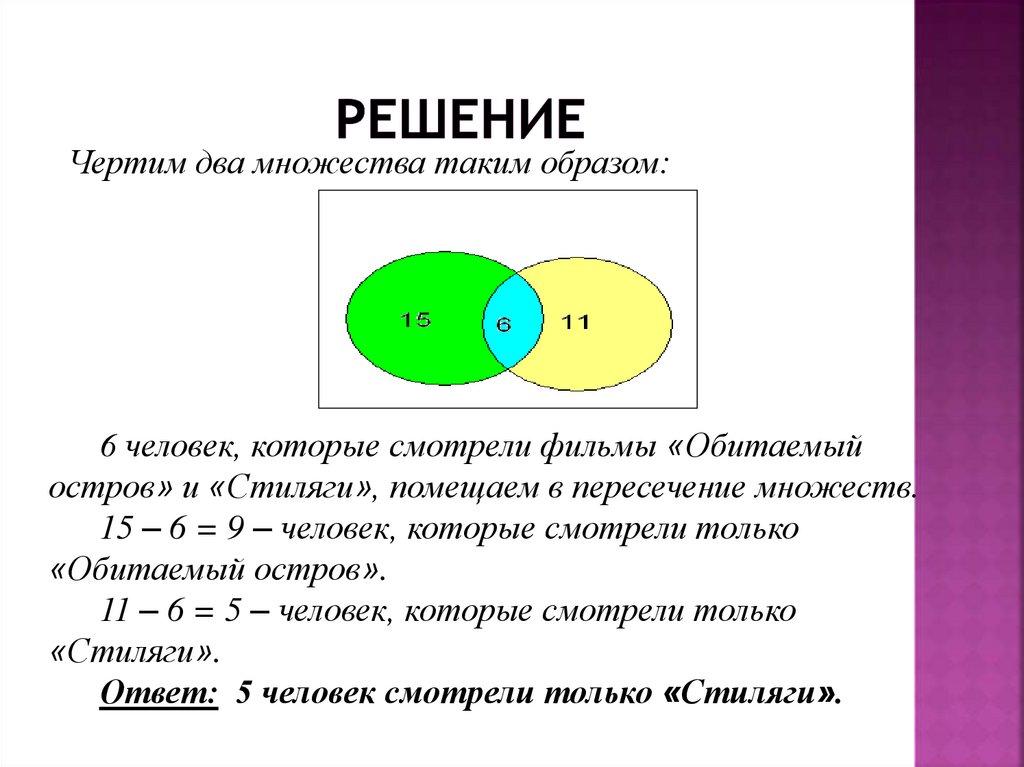
16. Решение

Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый
остров» и «Стиляги», помещаем в пересечение множеств.
15 – 6 = 9 – человек, которые смотрели только
«Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели только
«Стиляги».
Ответ: 5 человек смотрели только «Стиляги».

17.   Комбинированный метод

Пример
1.У Буратино есть 27 золотых монет. Но известно, что
Кот Базилио заменил одну монету на фальшивую, а она по весу
тяжелее настоящих. Как за три взвешивания на чашечных
весах без гирь Буратино определить фальшивую монету?
1652

18. Решение

Разделим монеты на 3 кучки по 9 монет. Положим на чаши
весов первую и вторую кучки; по результату этого
взвешивания мы точно узнаем, в какой из кучек находится
фальшивка (если весы покажут равенство, то она - в третьей
кучке). Теперь, аналогично, разделим выбранную кучку на три
части по три монеты, положим на весы две из этих частей и
определим, в какой из частей находится фальшивая монета.
Наконец, остается из трех монет определить более тяжелую:
кладем на чаши весов по 1 монете - фальшивкой является более
тяжелая; если же на весах равенство, то фальшивой является
третья монета из части. Задача решена.
Ответ: фальшивой является третья монета

19. 2.Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить

20. Решение

Как в результате можно получить 4 л? Нужно из
5-литрового сосуда отлить 1 л. А как это сделать?
Нужно в 3-литровом сосуде иметь ровно 2 л. Как их
получить?
Надо из 5-литрового сосуда отлить 3 литра.
Решение лучше и удобнее оформить в виде
таблицы:
Ходы 1
2
3
4
5
6
5л
5
2
2
-
5
4
3л
-
3
-
2
2
3

21. Задачи, решаемые с конца

Пример
Трое мальчиков имеют по некоторому количеству яблок.
Первый мальчик дает другим столько яблок, сколько каждый
из них имеет. Затем второй мальчик дает двум другим
столько яблок, сколько каждый из них теперь имеет; в свою
очередь и третий дает каждому из двух других столько,
сколько есть у каждого в этот момент. После этого у
каждого из мальчиков оказывается по 8 яблок. Сколько яблок
было у каждого мальчика вначале?

22. Решение

Решаем задачу с конца с помощью таблицы.
Таким образом, первоначально яблок у первого, второго и
третьего мальчиков было соответственно 13, 7, и 4.
Ответ: 13 яблок, 7 яблок, 4 яблока.
Номер мальчика
Число яблок в
конце
Число яблок до
передачи их
третьим
мальчиком
Число яблок до
передачи их
вторым мальчиком
Число яблок
первоначально
1
2
3
8
8
8
8: 2 = 4
8: 2 = 4
8 + 8 + 4 = 16
4: 2 = 2
4 + 2 + 8 = 14
16: 2 = 8
2 + 4 + 7 = 13
14: 2 = 7
8: 2 = 4

23. Выводы

Практикой доказано, что ребята, имеющие
хорошие математические навыки,
математическую логику, математический и
языковый интеллект успешны и по другим
предметам. Мы в этом убедились сами. И
достоверно доказано, что старение мозга
человека происходит медленнее, если он
занимается умственным трудом. Надеемся, что
эта работа будет увлекательной и полезной не
только для учащихся, но и для тех, кто уже давно
перешагнул этот порог.

24.

25.

26.

27.

28. Спасибо за внимание

29. Список литературы и web-ресурсов

Баврин И.И., Фрибис Е.А. Старинные задачи: Кн. Для учащихся. –
М.: Просвещение, 1994.- 128 с.: ил. – ISBN 5-09-005128-3.
Гарднер М. Математические головоломки и развлечения. – М.:
Мир, 1971. – 510 с.
Климченко Д.В. Задачи по математике для любознательных.
Чебоксары: Чувашгосиздат, 1963. – 43 с.
Лебедева И.В. Занимательные игры для детей. – Москва: ИКЦ
«МарТ»; Ростов н/Д: Издательский центр «МарТ», 2004. – 128 с.
Мерлин А.В., Мерлина Н.И. Задачи для внеклассной работы по
математике (5-11 классы): Учебное пособие. 2-е изд., испр. И доп.
Чебоксары: Изд-во Чуваш. Ун-та, 2002. 218 с.
365 задач на смекалку. – М.: АСТ-ПРЕСС КНИГА. -272 С. – (Умникам
и умницам)
http://golovolomka.hobby.ru/
http://golovolomka.narod.ru/
http://www.origami.ru/
http://www.izvilina.com/pd.html