Similar presentations:
Трудности, с которыми сталкивается обучающиеся при решении дробных рациональных уравнений
1.
Еловик Екатерина Петровна,учитель математики МОУ
«СОШ№17»
2.
Если люди отказываютсяверить в простоту
математики, то это только
потому, что они не понимают
всю сложность жизни.
Джон фон Нейман
:
3.
Уважаемые коллеги, трудности, с которымисталкивается обучающиеся при решении дробных
рациональных уравнений – это:
определить наименьший общий знаменатель
найти дополнительный множитель для каждой дроби
входящей в уравнение;
4. я приглашаю на мастер-класс для работы творческую группу в составе:
Я ПРИГЛАШАЮ НА МАСТЕР-КЛАСС ДЛЯ РАБОТЫТВОРЧЕСКУЮ ГРУППУ В СОСТАВЕ:
самого мотивированного члена группы (учитель
математики);
есть базовые знания, они помогут (учитель начальных
классов);
вселять веру в свои силы, убеждать, что всё получится
(психолог);
сидеть в постоянном напряжении, необходима
хорошая физическая подготовка (учитель физической
культуры).
5.
Найдем наименьший общий знаменательдробей, входящих в уравнение.
+
=
6. Как это правильно сделать?
7. Чтобы ошибки, свести к минимуму, при нахождении общего знаменателя при решении дробных рациональных уравнений предлагаю
ЧТОБЫ ОШИБКИ, СВЕСТИ К МИНИМУМУ, ПРИ НАХОЖДЕНИИОБЩЕГО ЗНАМЕНАТЕЛЯ ПРИ РЕШЕНИИ ДРОБНЫХ
РАЦИОНАЛЬНЫХ УРАВНЕНИЙ ПРЕДЛАГАЮ СЛЕДУЮЩИЙ
АЛГОРИТМ РЕШЕНИЯ ЭТОЙ ПРОБЛЕМЫ.
•Выписать знаменатели всех дробей в столбик;
• разложить на простые множители те знаменатели,
которые раскладываются;
Записать общий знаменатель так:
•из первого знаменателя выписываем все множители;
•из второго знаменателя выписываем множители,
которых еще нет, в общем знаменателе;
•из третьего знаменателя выписываем так же множители,
которых еще нет, в общем знаменателе;
Получили наименьший общий знаменатель
8. Чтобы ошибки, свести к минимуму, при нахождении общего знаменателя при решении дробных рациональных уравнений предлагаю
ЧТОБЫ ОШИБКИ, СВЕСТИ К МИНИМУМУ, ПРИ НАХОЖДЕНИИОБЩЕГО ЗНАМЕНАТЕЛЯ ПРИ РЕШЕНИИ ДРОБНЫХ
РАЦИОНАЛЬНЫХ УРАВНЕНИЙ ПРЕДЛАГАЮ СЛЕДУЮЩИЙ
АЛГОРИТМ РЕШЕНИЯ ЭТОЙ ПРОБЛЕМЫ.
Выписать знаменатели всех
дробей в столбик:
1 знаменатель: х-2
2 знаменатель: (х-2) (х-5)
3 знаменатель: х-5
Общий знаменатель: (х-2) (х-5)
9.
Затемсравниваем знаменатель первый дроби с
общим знаменателем (которые в столбике). Если
множители знаменателя первой дроби
совпадают с множителями общего знаменателя,
то дополнительных множителей не будет. Затем
сравниваем знаменатель второй дроби с общем
знаменателем. Не достающиеся множители
общего знаменателя, будут являться
дополнительными множителями для второй
дроби. И так находим для всех дробей
дополнительные множители.
10.
После нахождения дополнительных множителей мызаписываем все числители под общим знаменателем,
который у нас найден и записан в столбике как общий
знаменатель. А далее решаем как обычно, раскрываем
скобки в числителе, приводим подобные. Получаем
дробь равную нулю. Дробь равна нулю в том случае,
если числитель равен нулю, а знаменатель нет. Таким
образом, переходим к системе. Находим корни
уравнения, проверяем с ОДЗ и пишем ответ.
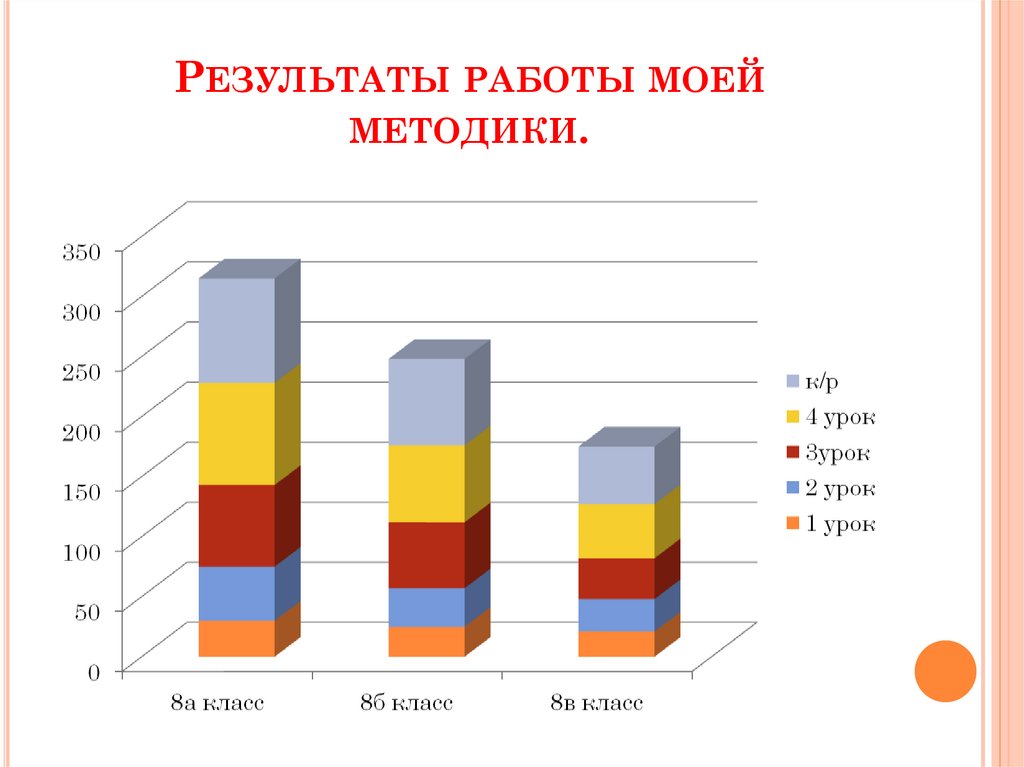
11. Результаты работы моей методики.
РЕЗУЛЬТАТЫ РАБОТЫ МОЕЙМЕТОДИКИ.
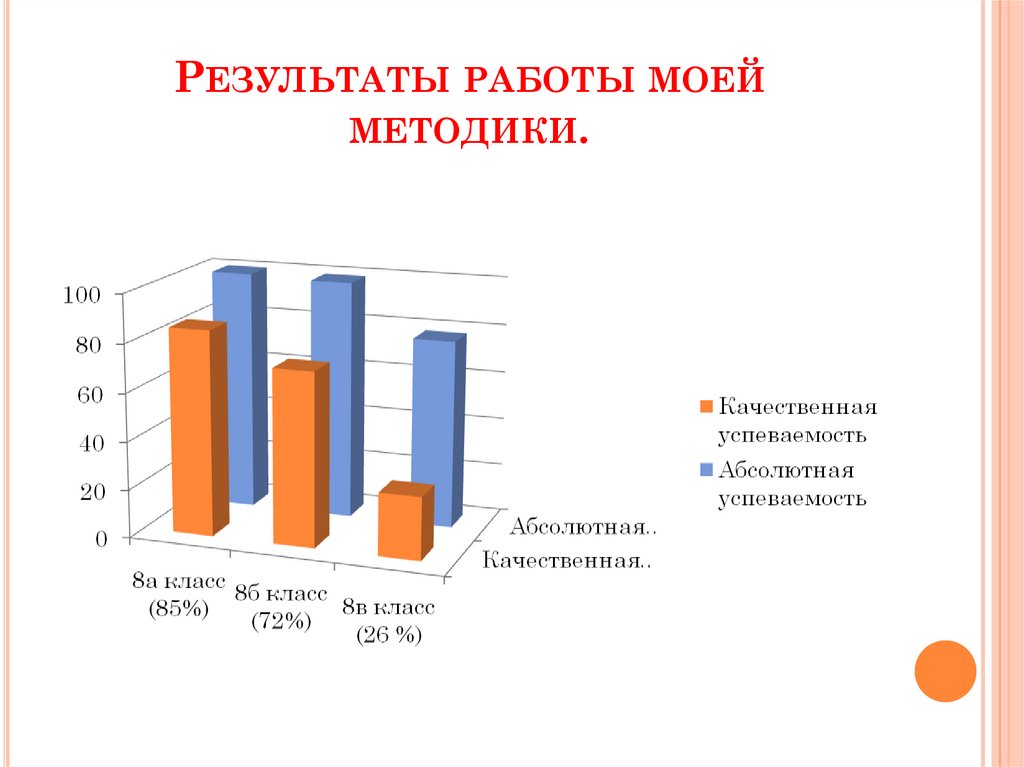
12. Результаты работы моей методики.
РЕЗУЛЬТАТЫ РАБОТЫ МОЕЙМЕТОДИКИ.
13. Пример №2
ПРИМЕР №2+
=
14. Проверяем работу творческой группы
ПРОВЕРЯЕМ РАБОТУ ТВОРЧЕСКОЙГРУППЫ
15. Рефлексия
РЕФЛЕКСИЯЧто
я делаю ?
С какой целью ?
Каковы результаты моей
деятельности ?
Как этого достичь ?
Можно ли сделать лучше ?
Что я буду делать дальше ?










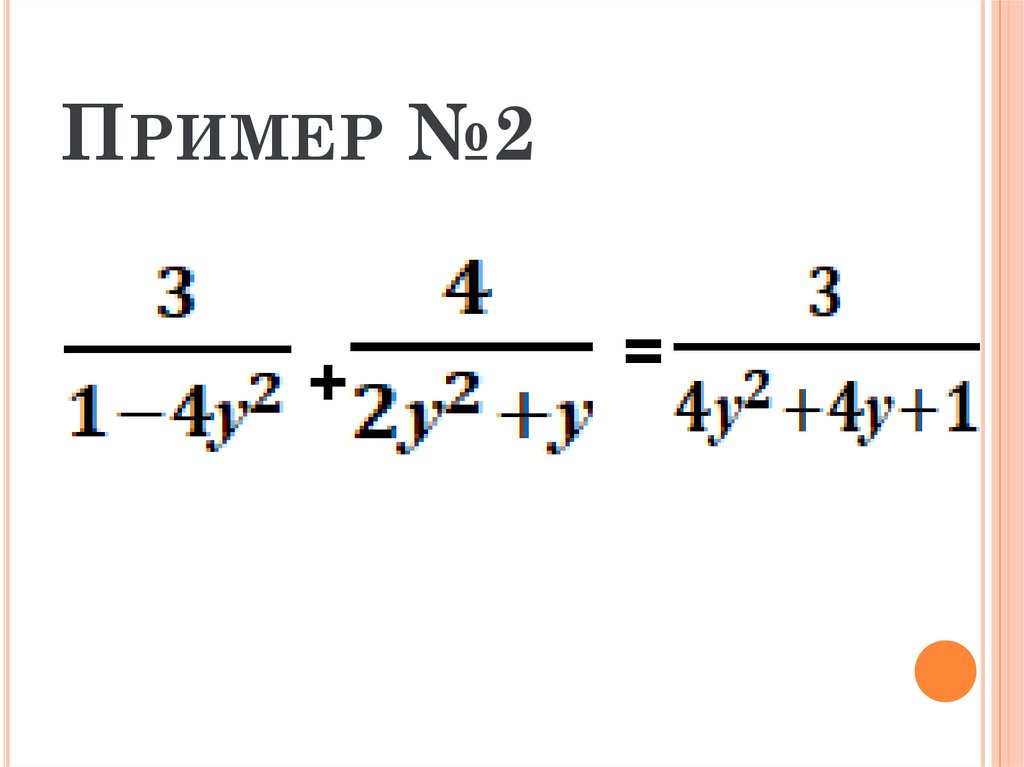


 mathematics
mathematics








