Similar presentations:
Производные процентные расчеты. Средние ставки
1.
Производные процентные расчетыСредние ставки
Замена всех усредняемых значений ставок на
среднюю процентную ставку не изменяет
результатов операции.
2.
Простые проценты. Пусть за последовательныепериоды n1, n2, …, nk начисляются простые
проценты по ставкам i1, i2, …, ik.
Имеет место равенство
3.
Сложные переменные во времени ставкипроцентов:
(1 iср ) (1 i1 ) (1 i2 ) (1 ik )
n1
N
n2
nk
iср (1 i1 ) (1 i2 ) (1 ik ) 1
N
n1
n2
nk
4.
Усреднение ставок при однородных операциях,различающихся суммами ссуд и процентными
ставками.
Если сроки операций одинаковы (n), то
k
P (1 ni
t 1
t
iср
cр
k
Pi
t 1
k
k
) Pt (1 nit ),
t 1
t t
P
t 1
k
t
Для сложных ставок:
iср n
n
P
(
1
i
)
t t
t 1
k
P
t 1
t
1
5.
Эквивалентность процентных ставок.Динамика процессов наращения и
дисконтирования определяется только
временнóй зависимостью множителя
наращения и дисконтного множителя и
не зависит от величины первоначальной и
конечной сумм.
Замена одного типа ставки на другой не
изменит отношения сторон в рамках
конкретного контракта, если от такой замены
соответствующие множители не изменятся.
Такие ставки называют эквивалентными.
6.
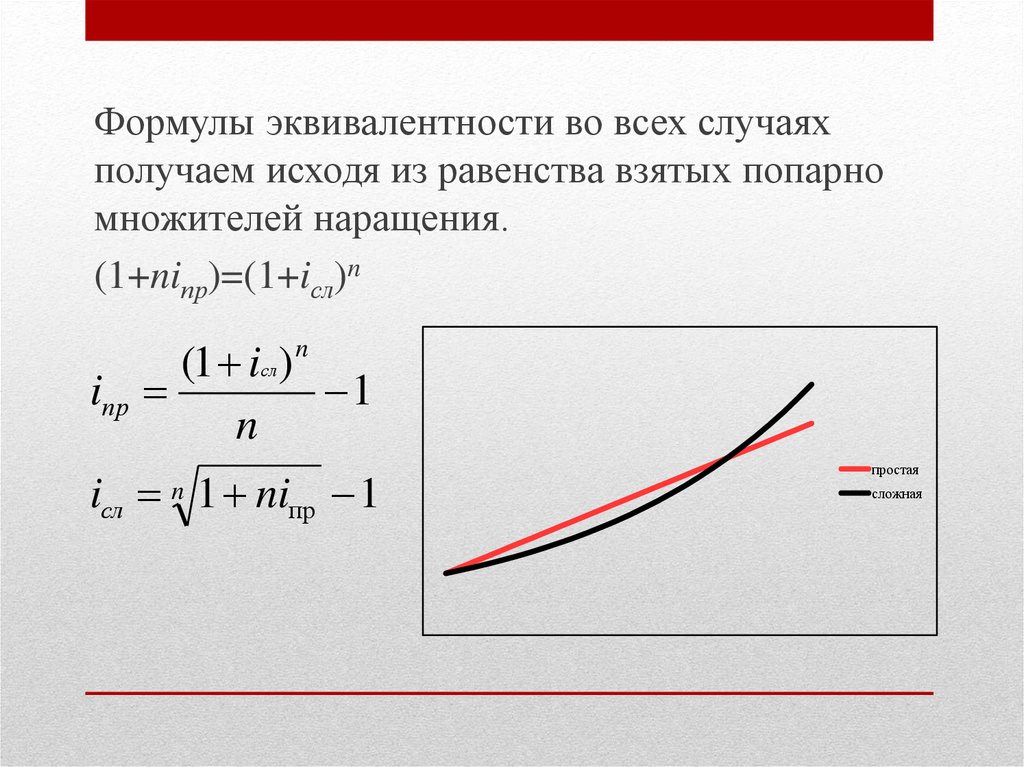
Формулы эквивалентности во всех случаяхполучаем исходя из равенства взятых попарно
множителей наращения.
(1+niпр)=(1+iсл)n
(1 iсл)
iпр
1
n
n
iсл n 1 niпр 1
простая
сложная
7.
Соотношения между численными значениямидвух эквивалентных друг другу различных
типов ставок зависят от срока контракта:
ставки, эквивалентные при одном сроке
контракта, как правило, неэквивалентны при
другом его значении.
8.
Необходимо найти величину простой учетнойставки (К=360), эквивалентной годовой простой
процентной ставке 40% (К=365) при условии,
что срок учета равен 255 дням.
Решение. Исходные формулы:
S = P(1+ni) и P = S(1–nd), т.е. S = P/(1–nd).
Приравняем множители наращения (n=t/K):
(1+(t/365)i)=1/(1–(t/360)d),
откуда получаем формулу эквивалентного
перехода
360i
360 0,4
d
0,3084 (30,84%).
365 ti 365 255 0,4
9.
Финансовая эквивалентность обязательств.Эквивалентными считаются платежи, которые
оказываются равными при приведении их
к одному моменту времени.
Пример. Имеются 2 обязательства. Условия
первого: выплатить 80 тыс. руб. через 1 квартал.
Условия второго: выплатить 100 тыс. руб. через
год. Ставка сравнения – 15% годовых.
S1
80
80
P1
77,108 тыс. руб.
1 n1i 1 3 0,15 1,0375
12
S2
100
P2
86,957 тыс. руб.
1 n2i 1 0,15
10.
PS1
S2
i
11.
Барьерная ставкаS1
S2
1 n1i0 1 n2i0
S 2 S1
i0
S1n2 S2 n1
Для примера:
i0
100 80
3
80 1 100
12
0,3636 (36,36%)
12.
При использовании сложных процентов:S1 (1 i0 ) n1 S 2 (1 i0 ) n2
(1 i0 )
i0
n 2 n1
n2 n1
S2
S 2 / S1
S1
1
13.
Консолидирование задолженности.Платежи S1, S2, …, Sm со сроками n1, n2, …, nm
заменяются одним в сумме S0 и сроком n0.
Определение размера платежа.
n1< n2< …< nm
S0 S j (1 (n0 n j )i ) Sk (1 (nk n0 )i ) 1
j
k
S0 S j (1 i)
j
(n1< n0< nm)
( n0 n j )
Sk (1 i) 1( nk n0 )
k
14.
Платежи в 1000 и 2000 руб. и сроками уплатычерез 2 и 3 года объединяются в один со сроком
2,5 года. Стороны согласились на применение
при конверсии сложной ставки 20% годовых.
Каков новый платеж?
S0=1000*(1+0,2)0,5+2000*(1+0,2)-0,5=2921,19 руб.
15.
Определение срока платежа.Уравнение эквивалентности при начислении
простых процентов:
S0 (1 n0i) 1 S j (1 n j i ) 1
j
1
S0
n0
1
1
i S j (1 n j i )
j
16.
Суммы в размере 10, 20 и 15 млн. руб. должныбыть выплачены через 60, 80 и 120 дней
соответственно. Стороны согласились заменить
их одним платежом в 50 млн. руб. при условии
12% годовых (К=360). Определить срок
консолидированного платежа.
P =10/(1+60/360*0,12) + 20/(1+80/360*0,12) +
+15/(1+120/360*0,12) = 43,708 млн.руб.
n0= 1/0,12*(50/43,708-1)=1,2 года (432 дня).
17.
Уравнение эквивалентности при начислениисложных процентов:
S0 (1 i)
n0
S j (1 i)
j
Q S j (1 i)
j
S0
ln
Q
n0
ln( 1 i )
n j
n j
18.
В общем случае решение задач измененияусловий выплат основывается на принципе
эквивалентности платежей. Метод решения
заключается в разработке соответствующего
уравнения эквивалентности.

















 finance
finance








