Similar presentations:
Half-Life and Activity
1.
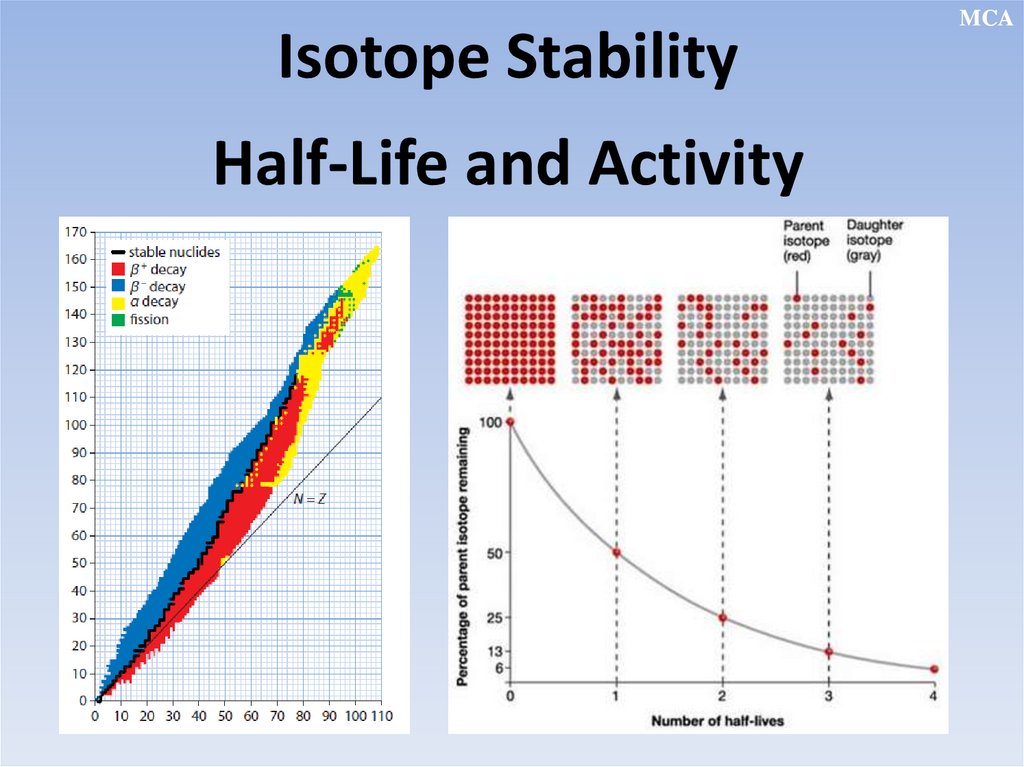
Isotope StabilityHalf-Life and Activity
MCA
2.
Topics / Key WordsIsotope stability
Neutron number against proton number graph
Radioactive decay as a random and spontaneous process
Decay curve
Half-life
Activity and law of radioactive decay
Decay constant
MCA
3.
Isotope StabilityMCA
Isotopes of the same element have similar chemical properties but
have very different nuclear properties (stability)
An unstable nucleus is one that randomly and spontaneously emits particles
and/or EM radiation in order to become more stable
Unstable isotopes are radioactive
Many elements have one or more stable isotopes and several
unstable isotopes
• Of the first 83 elements in the periodic table, 80 have stable isotopes
• All the elements with an atomic number over 82 (lead) are unstable
• Lead (82Pb) is considered the heaviest stable element
4.
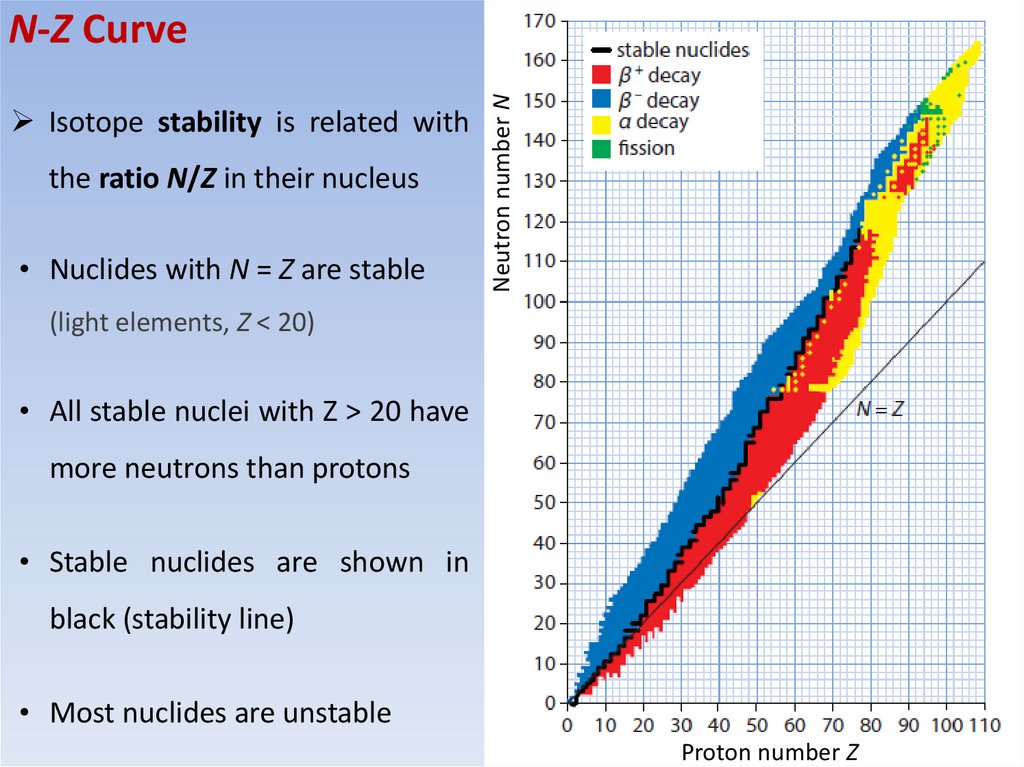
MCAIsotope stability is related with
the ratio N/Z in their nucleus
• Nuclides with N = Z are stable
Neutron number N
N-Z Curve
(light elements, Z < 20)
• All stable nuclei with Z > 20 have
more neutrons than protons
• Stable nuclides are shown in
black (stability line)
• Most nuclides are unstable
Proton number Z
5.
Randomness of Radioactive DecaysMCA
Rolling dice or flipping coins can help us to understand the
randomness of radioactive decays
Each die or coin represents an unstable nucleus
Dice Roller
Coin Flipper
• Roll 1000 dice at the same time
• It’s impossible to predict which dice will land on ‘3’
• It’s impossible to predict how many rolls we need for a particular dice to
land on ‘3’
6.
Radioactive Decay is Random and SpontaneousMCA
Radioactive decay is a
• spontaneous process because the rate of decay is not affected by any
external factors (such as pressure or temperature)
• random process because it is impossible to predict which nucleus will
decay next and it is impossible to predict when a particular nucleus will
decay
7.
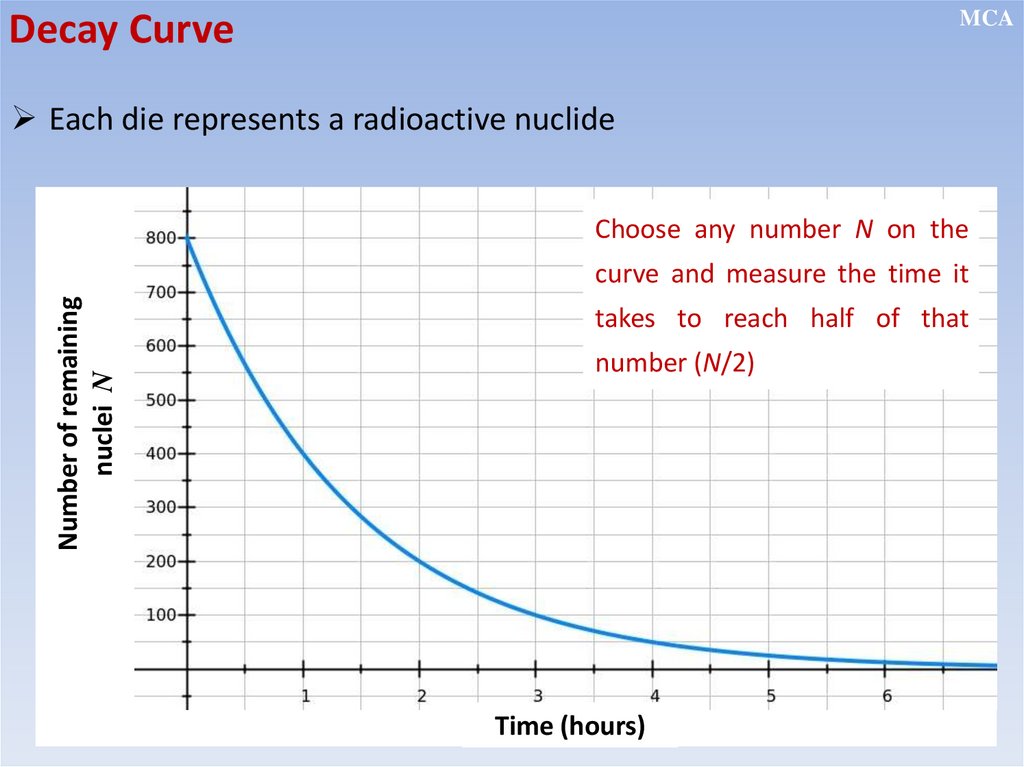
MCADecay Curve
Each die represents a radioactive nuclide
Choose any number N on the
Number of remaining
nuclei N
curve and measure the time it
takes to reach half of that
number (N/2)
Time (hours)
8.
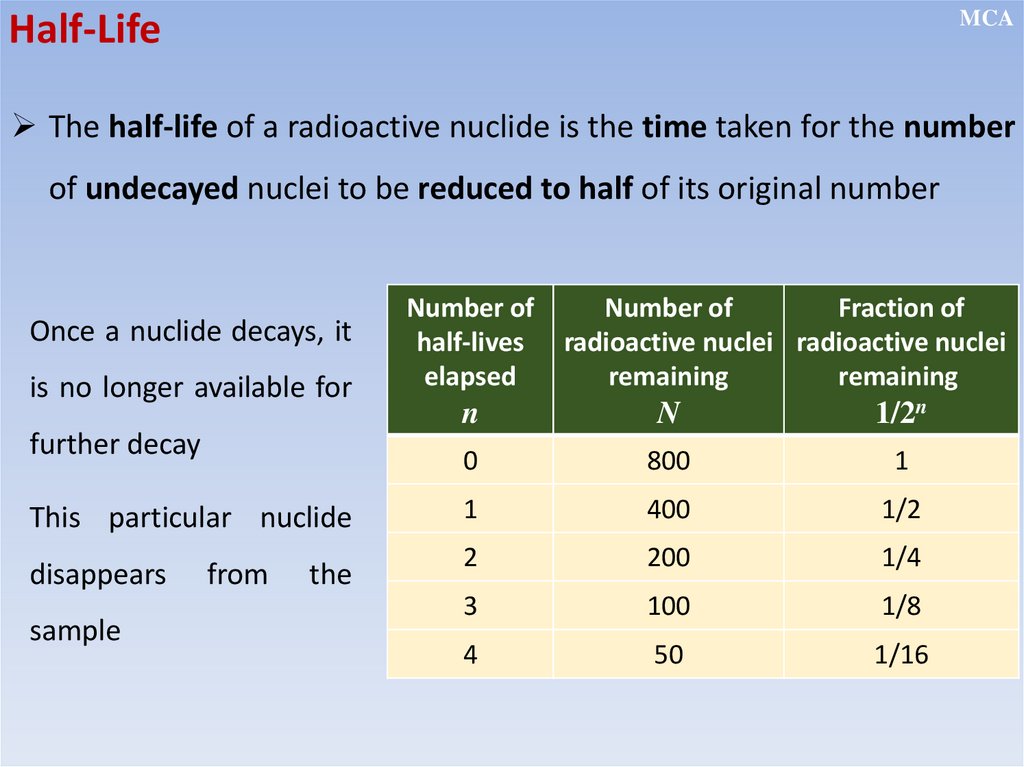
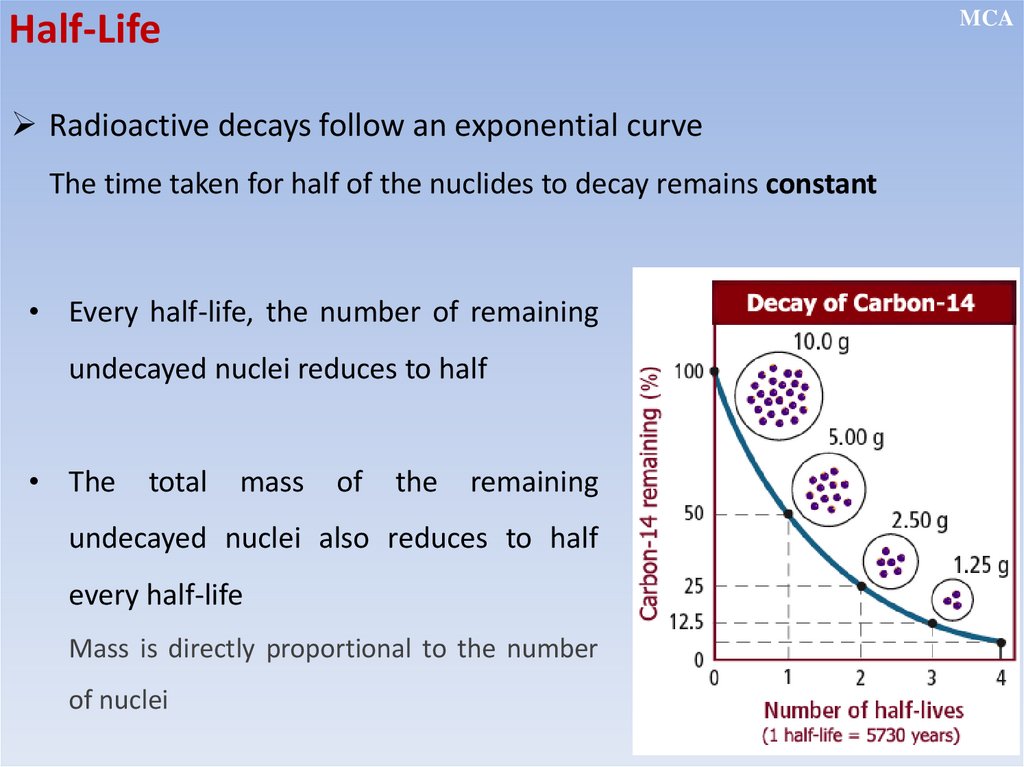
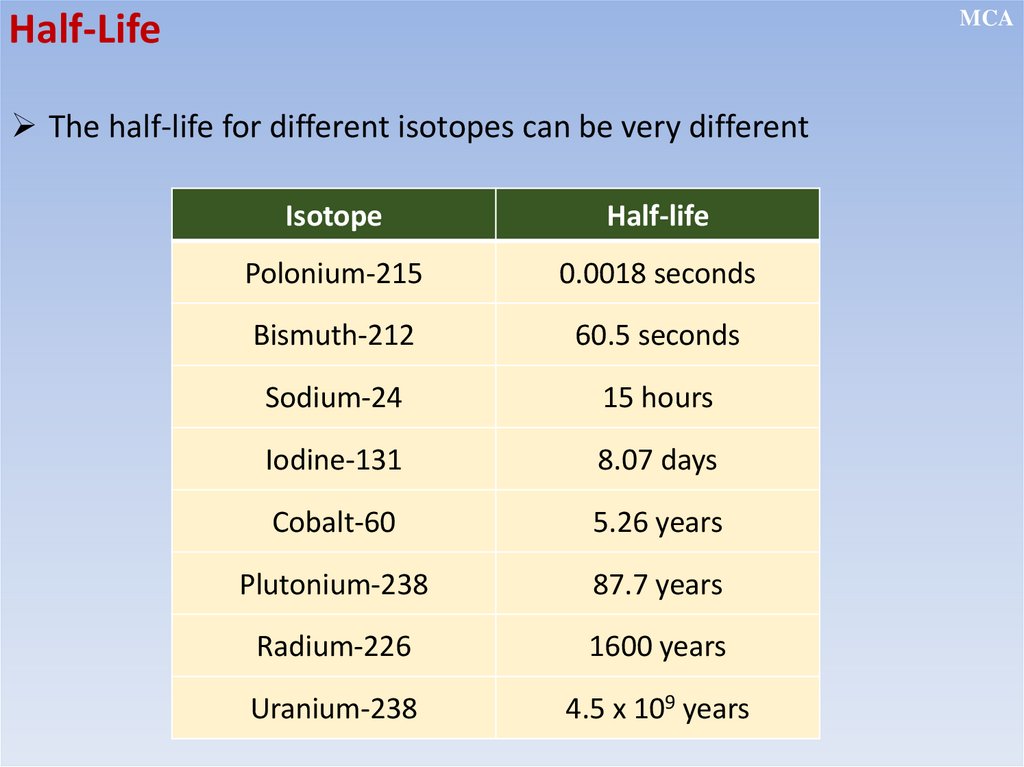
MCAHalf-Life
The half-life of a radioactive nuclide is the time taken for the number
of undecayed nuclei to be reduced to half of its original number
Once a nuclide decays, it
is no longer available for
further decay
This particular nuclide
disappears
sample
from
the
Number of
half-lives
elapsed
Number of
Fraction of
radioactive nuclei radioactive nuclei
remaining
remaining
n
N
1/2n
0
800
1
1
400
1/2
2
200
1/4
3
100
1/8
4
50
1/16
9.
MCAHalf-Life
Number of undecayed nuclei remaining after a time t has passed
Tip: the following formulas translate the definition of half-life and, thus, the
numbers found on the previous table; Usually, it is easier and faster to solve halflife problems by logical reasoning rather than by applying these formulas











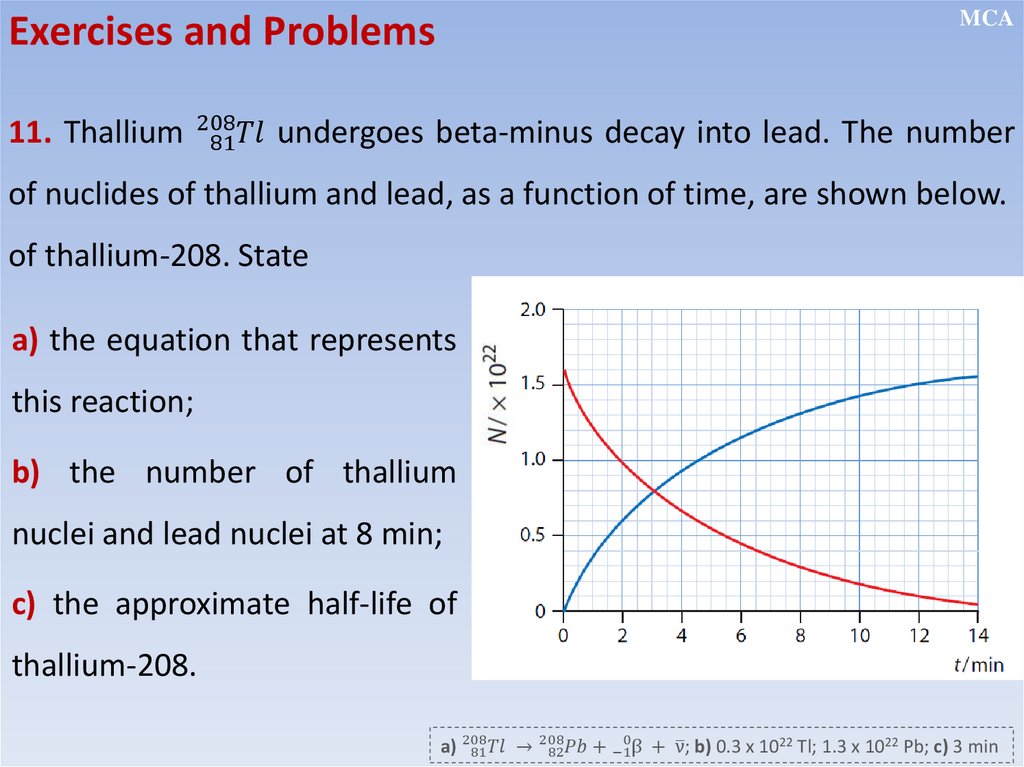

 chemistry
chemistry








