Системы счисления. Позиционные и непозиционные системы счисления. Представление чисел в позиционных системах счисления

1.

Тема урока
«Системы счисления.
Позиционные и
непозиционные системы
счисления. Представление
чисел в позиционных системах
счисления»
Преподаватель информатики:
Теплякова Анна Валерьевна

2.

Интеллектуальная программа учебного занятия:
1. Различие позиционных и непозиционных систем счисления
2. Развернутая и свернутая формы представления числа
3. Разновидности систем счисления, необходимость их
использования и область применения
4. Правила перевода чисел в различных позиционных системах
счисления
Ожидаемый результат:
1. знать назначение систем счисления, их виды, способы
представления чисел в десятичной и недесятичной системах
счисления
2. уметь пользоваться правилами перевода чисел в различных
позиционных системах счисления
3. Знать схему Горнера

3.

История появления чисел
1.
2.
3.
4.
5.
6.
7.
8.
Счет https://resh.edu.ru/subject/lesson/5620/start/15124/
Потребность в записи чисел
Единичная (унарная) система записи чисел
Вавилонская система
Египетская система
Славянская система
Римская система
Системы счисления
Система счисления – это математическая модель или знаковая
система, в которой числа записываются по определенным правилам с
помощью цифр.
Алфавит системы счисления – это используемый набор символов.
Основание системы счисления (q) – это количество символов в
алфавите.
Системы счисления
позиционные
непозиционные

4.

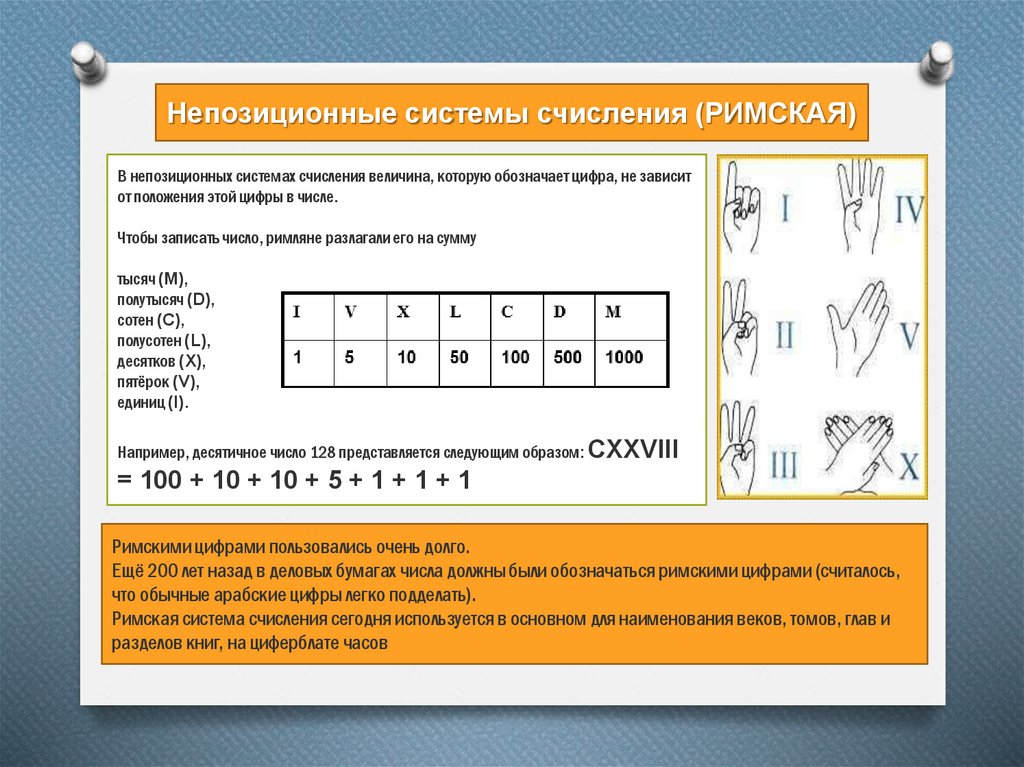
Непозиционные системы счисления (РИМСКАЯ)
В непозиционных системах счисления величина, которую обозначает цифра, не зависит
от положения этой цифры в числе.
Чтобы записать число, римляне разлагали его на сумму
тысяч (М),
полутысяч (D),
сотен (С),
полусотен (L),
десятков (X),
пятёрок (V),
единиц (I).
Например, десятичное число 128 представляется следующим образом: CXXVIII
= 100 + 10 + 10 + 5 + 1 + 1 + 1
Римскими цифрами пользовались очень долго.
Ещё 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось,
что обычные арабские цифры легко подделать).
Римская система счисления сегодня используется в основном для наименования веков, томов, глав и
разделов книг, на циферблате часов

5.

Непозиционные системы счисления
имеют ряд существенных недостатков:
• постоянная потребность введения новых знаков для записи больших
чисел;
• невозможно представлять дробные и отрицательные числа;
• сложно выполнять арифметические операции, т. к. не существует
алгоритмов их выполнения;
не применимы для компьютерной обработки информации по
причине отсутствия четких весовых закономерностей

6.

Позиционные системы счисления
Основное достоинство любой позиционной системы счисления – это
возможность записи произвольного числа ограниченным количеством
цифр.
Для записи чисел в позиционной системе счисления с основанием q
нужен алфавит, состоящий из q цифр.
(ДЕСЯТИЧНАЯ алфавит 0,1,2,3,4,5,6,7,8,9)
55510=5×100+5×10+5×1
В позиционных
системах счисления вес
цифры
(количественный
эквивалент)
зависит от ее позиции в
числе
Последовательность чисел, каждое из
которых задает «вес» соответствующего
разряда, называется базисом
позиционной системы счисления.
Представление числа в виде суммы разрядных слагаемых называется
развернутой формой записи числа в системе счисления с
основанием q. (5×100+5×10+5×1)
Сверная форма представления числа 55510

7.

Позиционные системы счисления
Система счисления
Основание (q)
Алфавит
2
0,1
8
0,1,2,3,4,5,6,7
10
0,1,2,3,4,5,6,7,8,9
Двоичная
используется для организации
машинных операций по
преобразованию информации
Восьмеричная
используется для составления
программ на языке машинных кодов
для более короткой и удобной записи
двоичных кодов (триады)
Десятичная
используется для ввода и вывода
информации
Шестнадцатиричная
используется для составления
программ на языке машинных кодов
для более короткой и удобной записи
двоичных кодов (тетрады)
0,1,2,3,4,5,6,7,8,9
16
A,B,C,D,E,F
двоичная
восьмеричная
десятичная
шестнадцатиричная
101,112
256,778
989,9910
10,ADF16

8.

Правила перевода чисел в
позиционных системах счисления
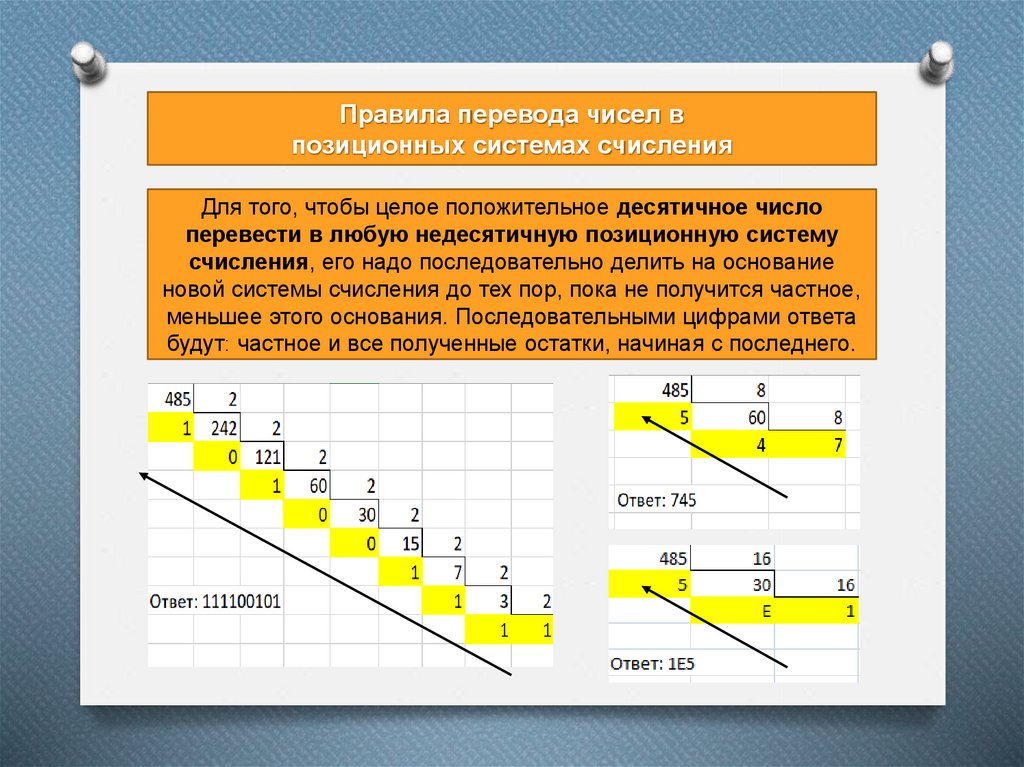
Для того, чтобы целое положительное десятичное число
перевести в любую недесятичную позиционную систему
счисления, его надо последовательно делить на основание
новой системы счисления до тех пор, пока не получится частное,
меньшее этого основания. Последовательными цифрами ответа
будут: частное и все полученные остатки, начиная с последнего.

9.

Правила перевода чисел в
позиционных системах счисления
Перевод произвольного положительного числа из
недесятичной системы счисления в десятичную
выполняется с помощью поразрядного представителя, т.е.
представления в виде суммы произведений цифр числа на
соответствующее степени основание.
1011012=1*25+0*24+1*23+1*22+0*21+1*20=32+0+8+4+0+1=4510
1011,12=1*23+0*22+1*21+1*20+1*2-1=8+0+2+1+0,5=11,510
658=6*81+5*80=48+5=5310
110,58=1*82+1*81+0*80+5*8-1=64+8+0+0,625=72,62510
F1416=15*162+1*161+4*160=3840+16+4=386010
AA,F16=10*161+10*160+15*16-1=160+10+0,9375=170,937510

10.

Правила перевода чисел в
позиционных системах счисления
Иногда бывает полезно преобразовывать развернутую форму
записи числа так, чтобы избежать возведения основания в степень.
Такую формулу представления числа называют схемой Горнера.

11.

Правила перевода чисел в
позиционных системах счисления
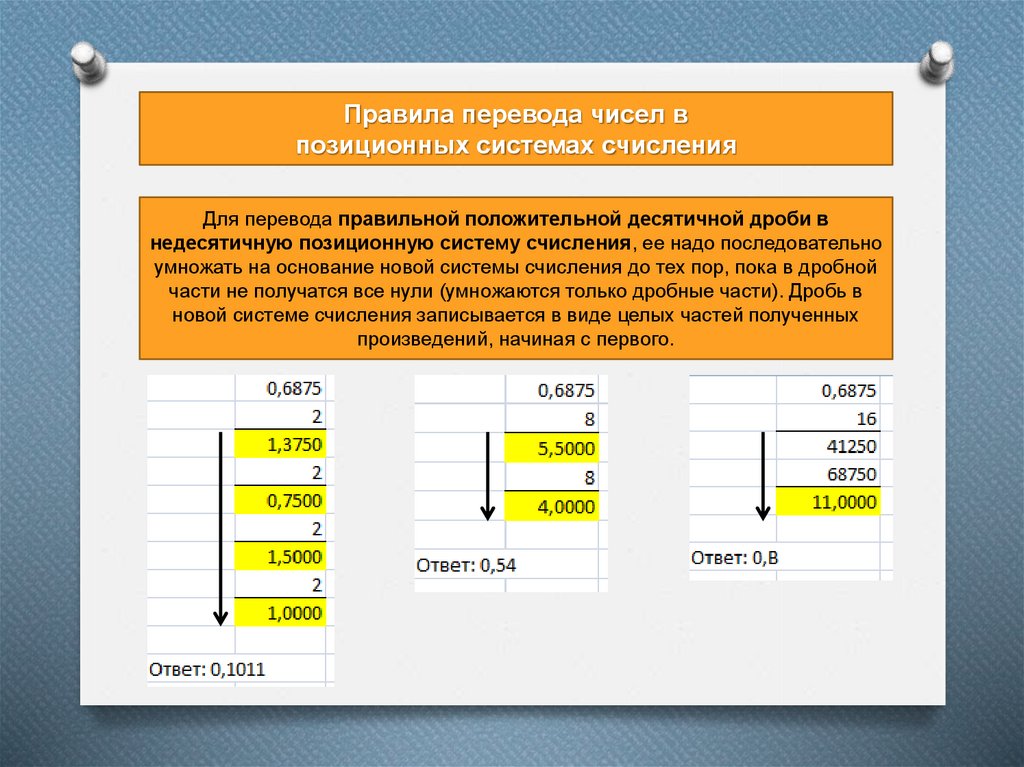
Для перевода правильной положительной десятичной дроби в
недесятичную позиционную систему счисления, ее надо последовательно
умножать на основание новой системы счисления до тех пор, пока в дробной
части не получатся все нули (умножаются только дробные части). Дробь в
новой системе счисления записывается в виде целых частей полученных
произведений, начиная с первого.

12.

Нахождение основания системы счисления
Десятичное число 57 в некоторой системе счисления записывается
как 212. Определите основание этой системы счисления.
Решение:
Представим число 212q в развёрнутой форме и приравняем к 57.
Пусть q – основание системы счисления, тогда в q-й системе счисления,
число 212 имеет следующее представление:
2*q2+1* q 1+2* q 0=5710
Решим квадратное уравнение:
2q2+1q -55=0
Д=1+440=441 (21)
q1=-5,5
q2=5
Так как основание системы счисления должно быть натуральным числом, то
q=5

13.

СИНКВЕЙН
первая строка – название темы
вторая строка – два прилагательных, описывающих тему в двух словах
третья строка – описание действия в рамках этой темы тремя словами
четвертая строка – фраза из четырех строк, показывающая отношение к
теме
последняя строка – синоним, который повторяет суть темы
Спасибо за внимание!
Творческих успехов!!!