Similar presentations:
Математика. Электронный курс
1.
Электронный курс по дисциплинеМатематика
УрФУ
2018
1
2.
Теория вероятностей и элементыматематической статистики
УрФУ
2018
2
3.
Лекция 14РАСЧЕТНАЯ РАБОТА 1: «МОНЕТКА»
3
4.
Задание к лабораторной работе1. Возьмите 10 монет одинакового достоинства, хорошо
перемешайте и выложите на стол. Сосчитайте количество
гербов. Запишите результат.
2.Повторите пункт 1 сто раз. Результаты оформите в виде
таблицы экспериментальных данных:
№ броска
1
…
100
Число
выпавших
гербов
7
…
3
4
5.
3. Сосчитайте, сколько раз выпало 0 гербов, 1 герб, 2 герба, 3герба,…, результаты оформите в виде статистического ряда:
Случайная величина X - число
выпадений гербов
xi 0 1 2 3 4 5 6 7 8 9 10
Часто 2 6 10 ………… … … … …
та ni
5
6.
4. Постройте полигон частот, гистограмму.5. Вычислите математическое ожидание случайной величины
X, ее дисперсию D и среднее квадратичное отклонение
.
6. На графике, показывающем полигон относительных частот
экспериментальных значений величины X, постройте кривую
нормального распределения с вычисленными выше
значениями математического ожидания и дисперсии.
6
7.
7.Сравните экспериментальный и теоретический графикивизуально.
8. Вычислите вероятности попадания случайной величины X
в интервалы a , a , a 2 , a 2 , a 3 , a 3 . и
сравните с экспериментальными данными.
7
8.
29. Вычислите критерий Пирсона и проверьте гипотезу о
нормальным характере распределения, приняв доверительную
вероятность 0,05 .
10. Постройте доверительный интервал для математического
ожидания величины X.
8
9.
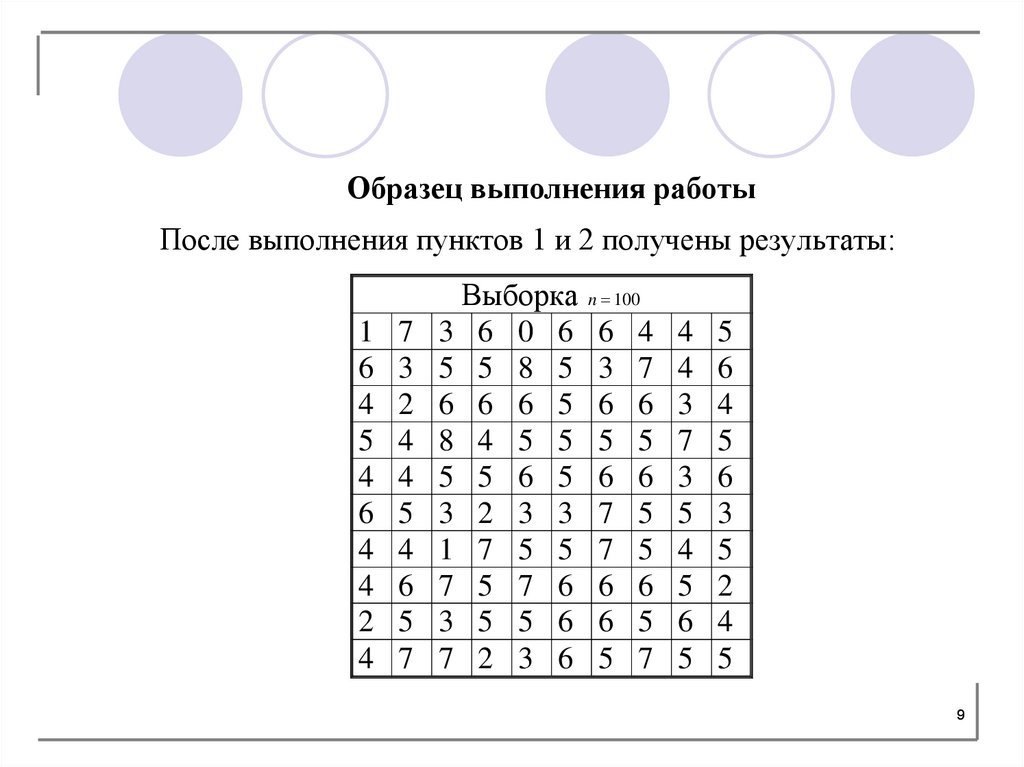
Образец выполнения работыПосле выполнения пунктов 1 и 2 получены результаты:
1
6
4
5
4
6
4
4
2
4
7
3
2
4
4
5
4
6
5
7
Выборка n 100
3 6 0 6 6 4
5 5 8 5 3 7
6 6 6 5 6 6
8 4 5 5 5 5
5 5 6 5 6 6
3 2 3 3 7 5
1 7 5 5 7 5
7 5 7 6 6 6
3 5 5 6 6 5
7 2 3 6 5 7
4
4
3
7
3
5
4
5
6
5
5
6
4
5
6
3
5
2
4
5
9
10.
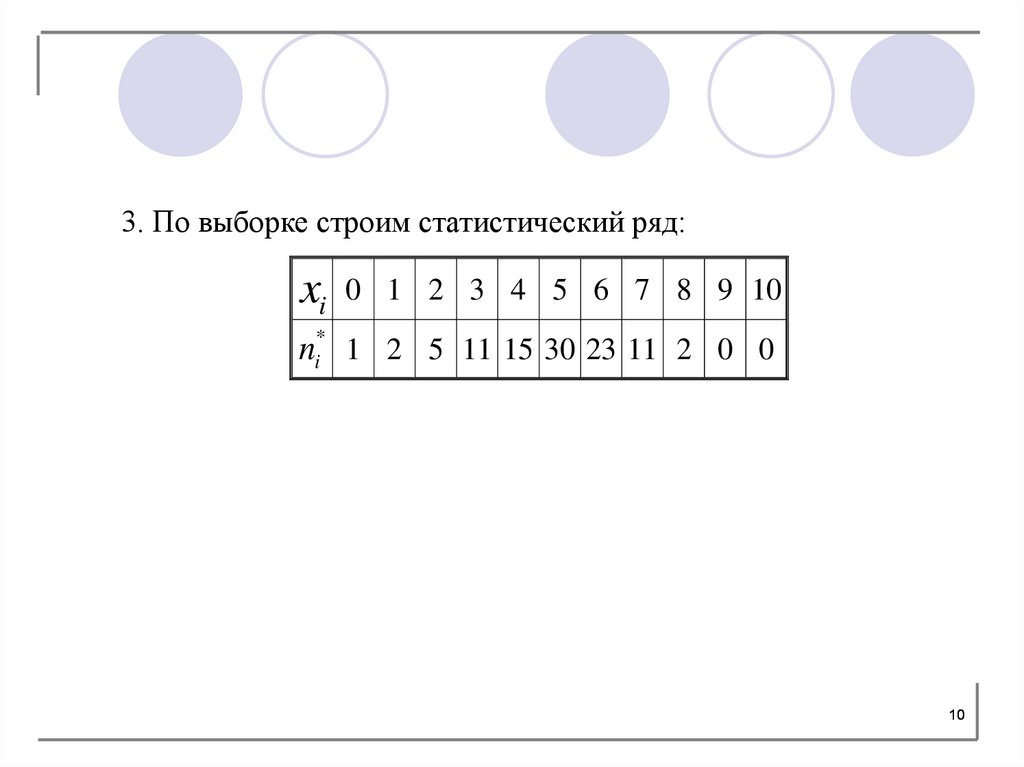
3. По выборке строим статистический ряд:xi 0 1 2 3 4 5 6 7 8 9 10
ni* 1 2 5 11 15 30 23 11 2 0 0
10
11.
*n
4. Полигон и гистограмма частот i i 0,1,...,10 ,
число значений xi равно 11.
Полигон
Гистограмма
35
35
30
30
25
25
20
20
15
15
10
10
5
5
0
0
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
11
12.
5. Числовые характеристики выборочного распределения.Выборочное среднее:
1 10 *
2 1 5 2 11 3 15 4 30 5 23 6 11 7 2 8
xB ni xi
4,860
n i 0
100
12
13.
Выборочная дисперсия:1 10 *
1 10 * 2
2
2
DB ni xi xB ni xi xB
n i 0
n i 0
2 12 5 22 11 32 15 42 30 52 23 62 11 7 2 2 82
4,8602
100
26,060 4,8602 2, 440.
Выборочное среднее квадратическое отклонение:
B DB 1,562 .
13
14.
В качестве точечных оценок параметров распределенияберем найденные выборочные средние:
a xB 4,860 , B 1,562 .
14
15.
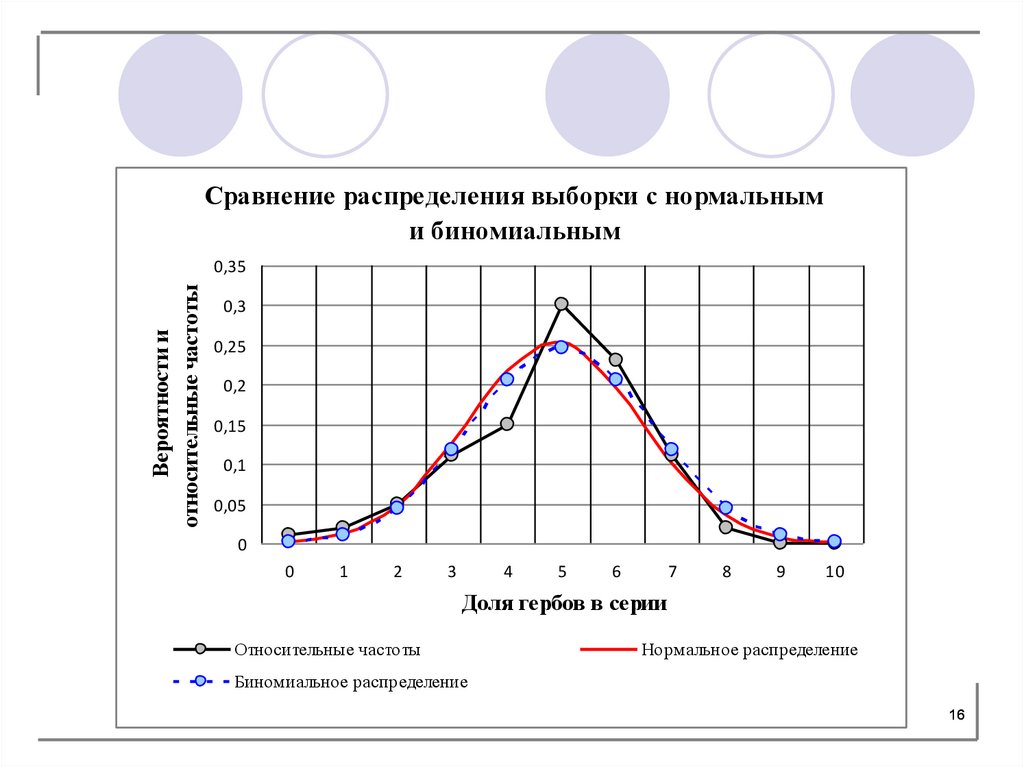
6,7. Построение кривых нормального и биномиальногораспределений, их сравнение с экспериментальным
распределением.
2
x a
1
2 2
e
Кривая нормального распределения
2
строится при полученных экспериментальных значениях
f x
параметров a 4 ,860 и 1,562 :
15
16.
Сравнение распределения выборки с нормальными биномиальным
Вероятности и
относительные частоты
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5
6
7
8
9
10
Доля гербов в серии
Относительные частоты
Нормальное распределение
Биномиальное распределение
16
17.
8. Теоретические вероятности попадания в интервалы.a
a
P{ X } Ф
Ф
Ф( x) - функция Лапласа,
, где
x
Ф( x )
t2
2
1
e dt ,
2 0
Ф x Ф x .
Значения функции Лапласа берутся из таблиц.
17
18.
a aa a
P{a X a } Ф
Ф
Ф 1 Ф 1 2Ф 1 0,6827 .
Аналогично
P{a 2 X a 2 } 2Ф 2 0,9545 ,
P{a 3 X a 3 } 2Ф 3 0,9973 .
18
19.
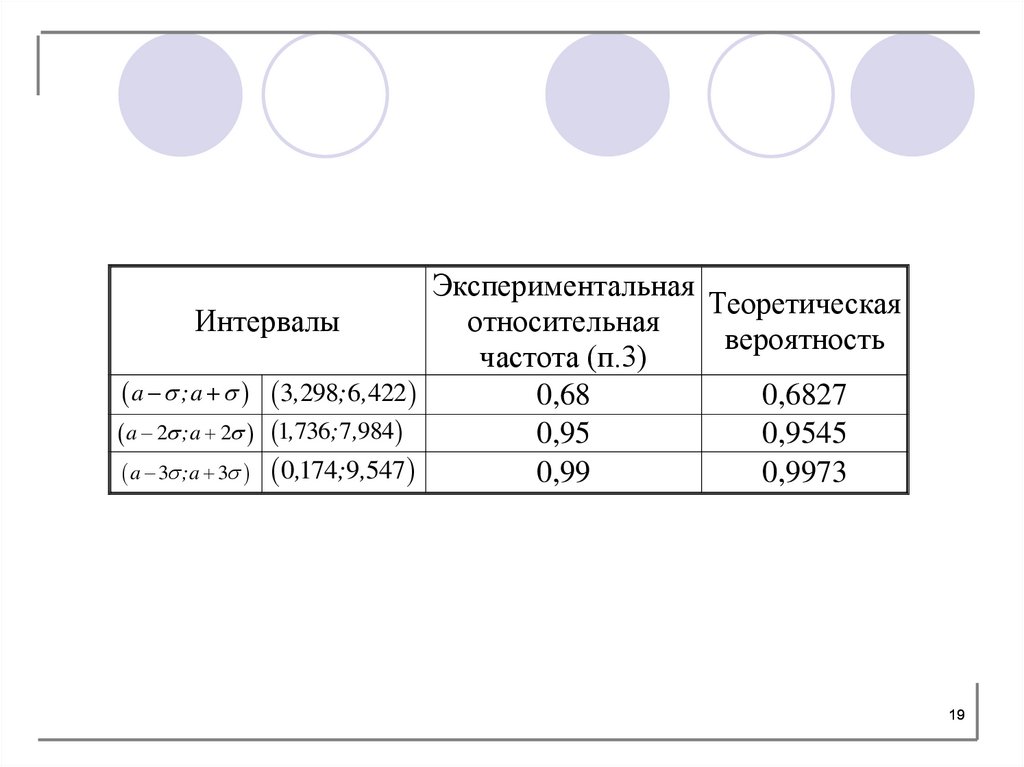
ЭкспериментальнаяТеоретическая
Интервалы
относительная
вероятность
частота (п.3)
a ;a 3,298;6,422
0,68
0,6827
a 2 ;a 2 1,736;7,984
0,95
0,9545
a 3 ;a 3 0,174;9,547
0,99
0,9973
19
20.
29. Вычисление критерия Пирсона и проверка гипотез о
нормальном (или биномиальном) распределении выборки.
Критерий Пирсона :
2
2
набл
10
n np
i 0
npi
*
i
2
i
,
*
n
где i – экспериментальные частоты, а pi – теоретические
вероятности (найденные с помощью функции нормального
распределения или по формуле Бернулли), соответствующие
значениям случайной величины X (количества гербов при
выкладывании 10 монет).
20
21.
Для биномиального распределения вероятности вычисляются поm m
n m
P
(
m
)
C
p
(1
p
)
n
формуле Бернулли n
( p 0,5 ):
xi
10 xi
1 1
pi binom C 1
2 2
xi
10
10
1
C
2
xi
10
,
для нормального распределения берутся значения плотности
вероятности нормального распределения,
xi a 2
1
2 2
pi norm f xi
e
,
2
где среднее значение и СКО взяты из оценок по выборке:
sB 1,570 , a xB 4,860 .
21
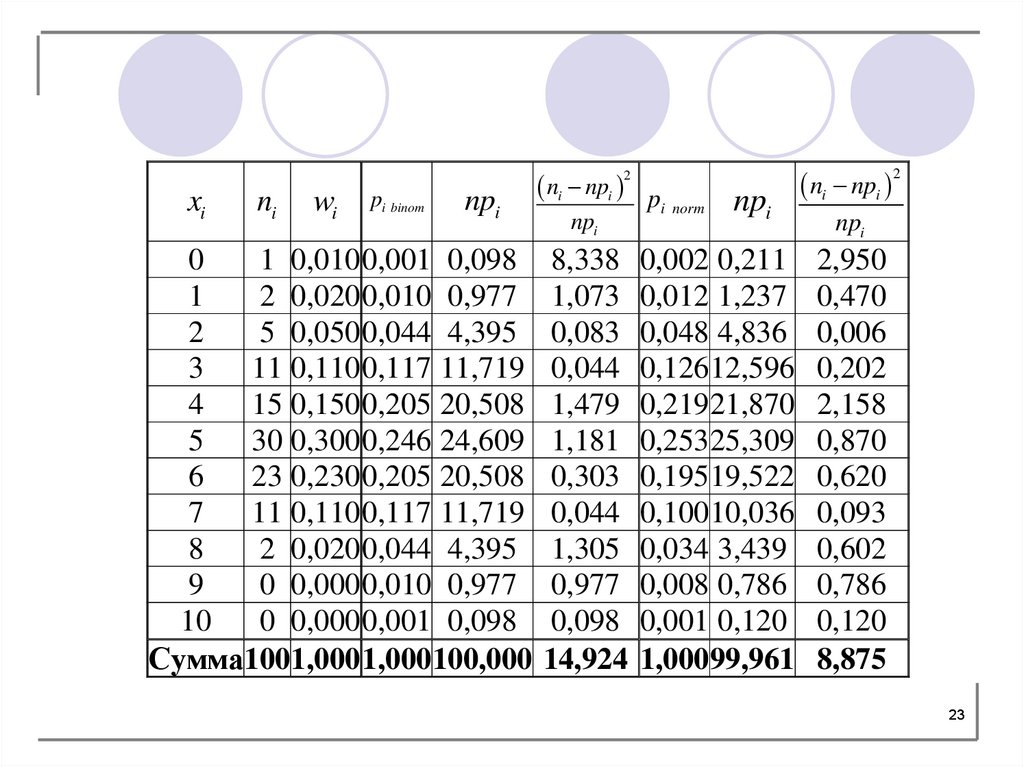
22.
В таблице на следующем слайде в четвертом столбце приведенывероятности, вычисленные по формуле Бернулли, в седьмом
столбце – значения плотности вероятности нормального
распределения, далее вычисляются слагаемые набл .
2
23.
n npini npi p
npi i
i norm
2
xi
ni
wi
pi binom
npi
npi
0
1 0,010 0,001 0,098 8,338 0,002 0,211
1
2 0,020 0,010 0,977 1,073 0,012 1,237
2
5 0,050 0,044 4,395 0,083 0,048 4,836
3
11 0,110 0,117 11,719 0,044 0,12612,596
4
15 0,150 0,205 20,508 1,479 0,21921,870
5
30 0,300 0,246 24,609 1,181 0,25325,309
6
23 0,230 0,205 20,508 0,303 0,19519,522
7
11 0,110 0,117 11,719 0,044 0,10010,036
8
2 0,020 0,044 4,395 1,305 0,034 3,439
9
0 0,000 0,010 0,977 0,977 0,008 0,786
10
0 0,000 0,001 0,098 0,098 0,001 0,120
Сумма1001,000 1,000100,000 14,924 1,00099,961
2
npi
2,950
0,470
0,006
0,202
2,158
0,870
0,620
0,093
0,602
0,786
0,120
8,875
23
24.
В последней строке шестого и девятого столбцов приведены2
экспериментальные значения критерия
набл : при сравнении с
2
нормальным распределением
набл 8,875 , при сравнении с
2
биномиальным распределением набл 14,924 .
При n распределение этой случайной величины, независимо
от того, каков закон распределения генеральной совокупности,
2
стремится к распределению Пирсона
с числом степеней свободы
q 1 k , где k – число параметров генерального распределения,
оцениваемых на основании наблюденных данных.
25.
а) Сравнение с нормальным распределением.Так как оба параметра распределения генеральной совокупности
оцениваются по данным выборки, число степеней свободы
11 3 8 .
2
По таблице распределения для 8 и 0,05 находим
2
критическую точку кр 0,05;8 15,507 .
2
набл
8,875 кр2 15,507 , гипотеза о нормальным
Так как
характере распределения случайной величины X не отвергается.
26.
б) Сравнение с биномиальным распределением.Так как единственный параметр распределения генеральной
совокупности, p 0,5 , не оценивается по данным выборки, число
степеней свободы 11 1 10 .
2
По таблице распределения
для 10 и 0,05 находим
2
критическую точку кр 0,05;10 18,307 .
2
2
14
,
924
кр 18,307 , гипотеза о биномиальном
Так как набл
характере распределения случайной величины X не отвергается.
27.
Таким образом, на принятом уровне значимости 0,05можно считать, что данные выборки распределены по
биномиальному закону с p 0,5 , n 100 ; с тем же основанием
можно считать, что данные выборки распределены по
нормальному закону с a xB 4,860 , sB 1,570 .
27
28.
10. Доверительный интервал для математического ожиданиявеличины X .
Считая, что величина X распределена по нормальному
закону с найденными ранее a xB 4,860 , B 1,562 и
принимая, что доверительная вероятность 0,05 , найдем
доверительный интервал I 0 ,95 для математического ожидания
величины X :
t sB
I1 xB , xB ,
n
,
28
29.
где sB – исправленное среднеквадратичное отклонение,sB
n
100
DB
2, 440 1, 570 ,
n 1
99
t – критическая точка (квантиль) распределения Стьюдента,
из таблиц t0 ,05 2, 306 .
t sB
n
2, 306 1, 570
0, 362
,
10
I 0 ,95 4,860 0,362; 4,860 0,362 4,498; 5,222
29
30.
Таким образом, на основании данного опыта можноутверждать, что с вероятностью 0,95 среднее количество
гербов в серии из 10 выбрасываний лежит в интервале
I 0 ,95 4, 498; 5, 222 .
30

























 mathematics
mathematics








