Similar presentations:
Случайные погрешности
1.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФФГБОУ ВО «ЮГОРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Высшая нефтяная школа
Метрологические основы химического анализа
«СЛУЧАЙНЫЕ ПОГРЕШНОСТИ»
старший преподаватель Смородинова Т.Н.
t_smorodinova@ugrasu.ru
2.
Случайные величины и их свойстваСлучайная
величина
- переменная величина, которая с
определенной вероятностью принимает различные значения.
дискретные и непрерывные
Примеры:
Непрерывные – температура, объем, результаты гравиметрического
анализа
Дискретные – число радиоактивных распадов, число квантов в
рентгеноспектральном анализе
2
3.
Случайные величины и их свойстваФункция распределения случайной величины Х – это функция F(x),
определяющая для каждого значения x вероятность того, что случайная
величина X примет значение меньшее, чем x.
интегральная и дифференциальная
3
4.
Случайные величины и их свойстваЭто вероятность того, что случайная величина х принимает значения,
меньшие некоторой заданной величины x0:
неубывающая
диапазон от 0 до 1
Вероятность того, что случайная величина находится в диапазоне от
x1 до x2 равна:
Вид интегральной функции
распределения случайной величины
4
5.
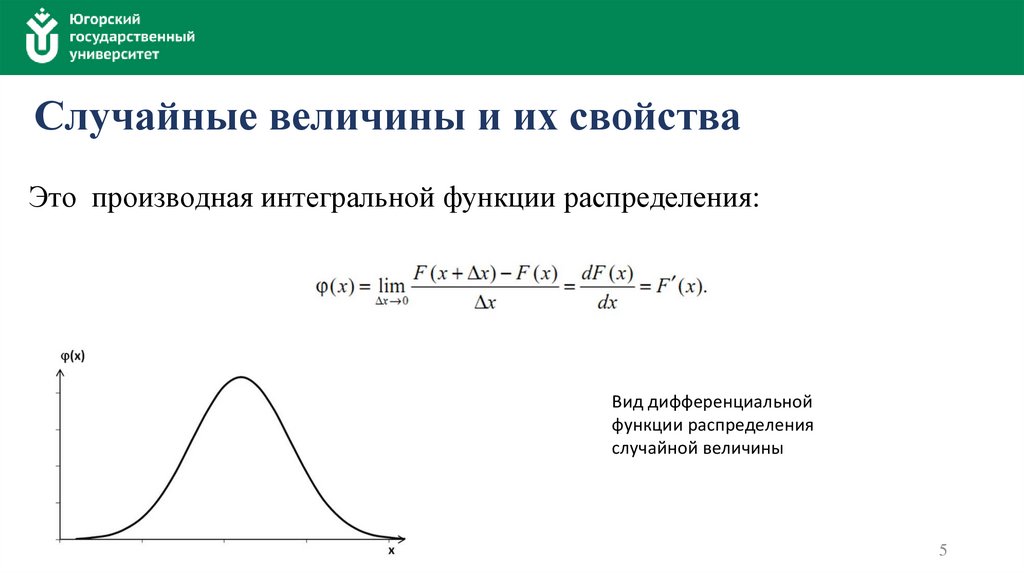
Случайные величины и их свойстваЭто производная интегральной функции распределения:
Вид дифференциальной
функции распределения
случайной величины
5
6.
Математическоеожидание
среднеарифметическое значение
и
Математическое ожидание — это то численное значение, к которому в обычных
условиях стремится среднее арифметическое результатов измерений, если
эксперимент повторять бесконечное число раз.
Генеральная совокупность - это бесконечно большой массив значений
аргумента, для которого определено распределение вероятности.
Выборка – это конечный и сравнительно небольшом массив значений
Среднее значение
аргумента.
Среднее арифметическое
Среднее геометрическое
Медиана
это число, которое
находится в середине
этого набора, если
его упорядочить по
6
возрастанию
7.
Математическоеожидание
среднеарифметическое значение
и
Чтобы найти медиану результаты измерений всегда располагают в ранжированный ряд
в порядке возрастания их значений
Если n - нечетное число, то медиана равна среднему значению
Если n - четное число, то медиана равна полусумме двух средних значений
Мода – наиболее часто встречающееся значение случайной величины при большой
серии измерений.
Пример 1: Рассчитайте арифметическое и геометрическое среднее значение для
выборок:
2,5 2,6 2,7 2,7 2,8
2,5 2,6 2,7 2,7 3,2
Пример 2: Рассчитайте медиану и моду для серии значений:
25 25 26 27 30
7
25 25 26 27 29 30
8.
Свойства математическогоожидания
среднего
значения
Математическое ожидание константы равно самой константе:
и
Математическое
ожидание произведения
константы на выборку равно
произведению константы на математическое ожидание выборки:
Математическое ожидание суммы равно сумме математических ожиданий:
Если существует некая функция
, то математическое
ожидание этой функции будет равно функции от математических ожиданий её
аргументов:
8
9.
Генеральная и выборочная дисперсияКритерии воспроизводимости:
Отклонение от среднего значения
Среднее отклонение от среднего
Среднее отклонение от медианы
Размах варьирования
Стандартное отклонение
Дисперсия
Генеральная дисперсия – описывает разброс функции распределения относительно
математического ожидания.
9
10.
Генеральная и выборочная дисперсияДисперсия – это среднее арифметическое квадратное отклонение от среднего значения
(для малых выборок n<30).
Число степеней свободы (f или n-1) – это число независимых переменных в выборочной
совокупности за вычетом числа связей между ними.
10
11.
Закон сложения и свойства дисперсий.Дисперсия, как и любая математическая функция, обладает рядом свойств:
1. Дисперсия константы равна нулю:
2. Если из каждого члена выборки можно вынести константу, то из дисперсии также можно вынести
квадрат этой константы:
3. Если одна выборка представляет из себя сумму выборок, то её дисперсия равна сумме дисперсий этих
выборок:
4. Если существует некая функция y, зависящая от выборок Xi, то дисперсия этой функции равна сумме
произведений квадратов частных производных данной функции на дисперсии этих выборок:
5. При увеличении числа измерений дисперсия среднего уменьшается.
11
12.
Стандартные отклонения и расчет погрешностиСтандартное отклонение – это оценка средней погрешности отклонений каждого
результата в серии от центра выборки, т.е. от среднего.
Относительно стандартное отклонение (коэффициент вариации) – это характеризует
относительную погрешность в долях или в процентах.
Примеры:
Sr(x) = n 10-3 - титриметрия, гравиметрия (высокая воспроизводимость)
Sr(x) от 0,005 до 0,10 – тест-методы (низкая воспроизводимость)
12
13.
Распределения случайных величинОсновные виды распределения случайных величин:
Нормальное (распределение Гаусса);
Распределение Стьюдента;
Усеченное нормальное;
Логнормальное;
Равномерное;
Треугольное.
13
14.
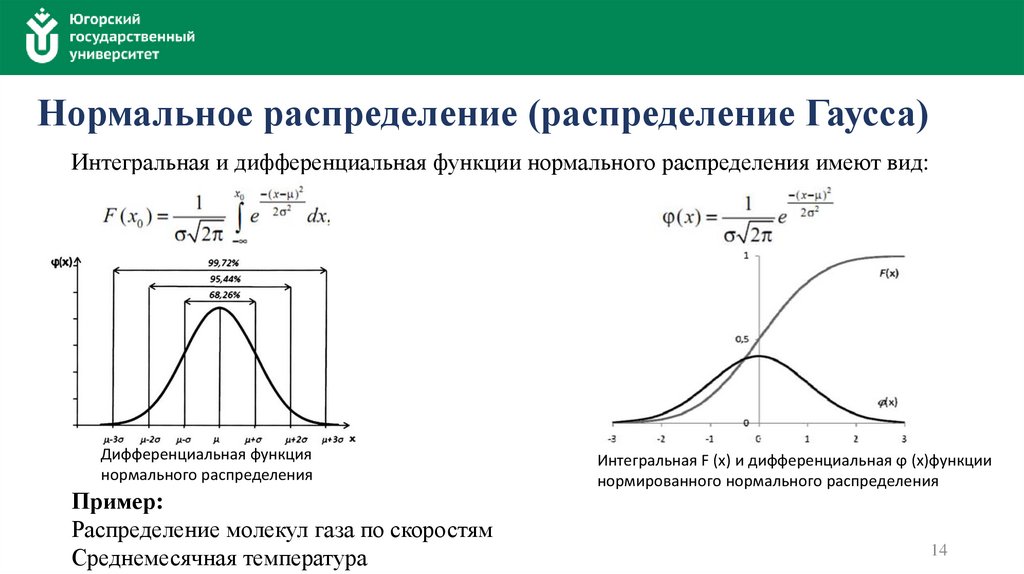
Нормальное распределение (распределение Гаусса)Интегральная и дифференциальная функции нормального распределения имеют вид:
Дифференциальная функция
нормального распределения
Пример:
Распределение молекул газа по скоростям
Среднемесячная температура
Интегральная F (x) и дифференциальная ϕ (x)функции
нормированного нормального распределения
14
15.
Характеристики нормального распределенияФункция нормального распределения имеет максимум
Функция симметрична относительно математического ожидания и, следовательно,
положительные и отрицательные отклонения равновероятны.
Функция имеет две симметричные точки перегиба
и
отвечающие условию
Дифференциальная функция резко падает за точками перегиба, и 95 % всех значений
случайной величины находятся в интервале от
15
16.
Распределение Стьюдента (t - распределение)На практике распределение Стьюдента используется в диапазоне (2≤n≤20).
График дифференциальной функции распределения Стьюдента при различных значениях
n
В соответствии с распределением Стьюдента результат анализа с заданной вероятностью
находится в интервале:
16
17.
Доверительный интервал идоверительная вероятность
Доверительный интервал – это интервал, в котором с определенной вероятностью
находится значение случайной величины.
где t – коэффициент Стьюдента для доверительной вероятности Р и числа степеней
свободы f;
S – абсолютное стандартное отклонение измеряемой величины, рассчитанное для
выборки из n данных.
Доверительная вероятность (Р) – показывает сколько результатов измерений попадает в
данный интервал.
17
18.
Доверительныйвероятность
интервал
и
доверительная
Доверительные границы
Представление результата:
где А - результат измерения; ∆ - погрешность анализа; Р - доверительная вероятность.
- нижняя доверительная граница
- верхняя доверительная граница
18
19.
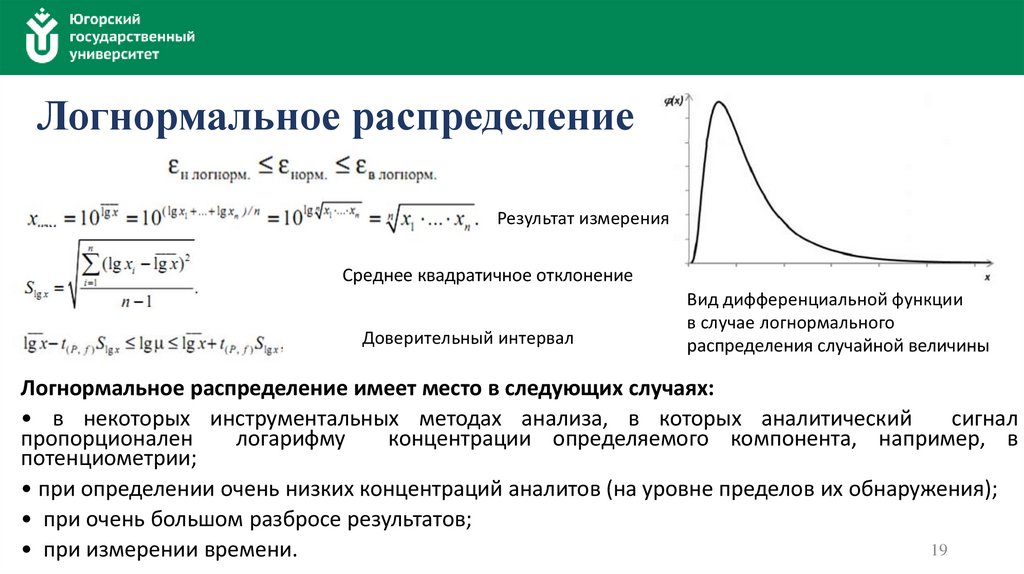
Логнормальное распределениеРезультат измерения
Среднее квадратичное отклонение
Доверительный интервал
Вид дифференциальной функции
в случае логнормального
распределения случайной величины
Логнормальное распределение имеет место в следующих случаях:
• в некоторых инструментальных методах анализа, в которых аналитический
сигнал
пропорционален
логарифму
концентрации определяемого компонента, например, в
потенциометрии;
• при определении очень низких концентраций аналитов (на уровне пределов их обнаружения);
• при очень большом разбросе результатов;
19
• при измерении времени.
20.
Равномерное распределениеГрафик дифференциальной
функции равномерного
распределения
Все значения случайной величины равновероятны и находятся в интервале:
Результаты измерений и квадратичное отклонение:
20
21.
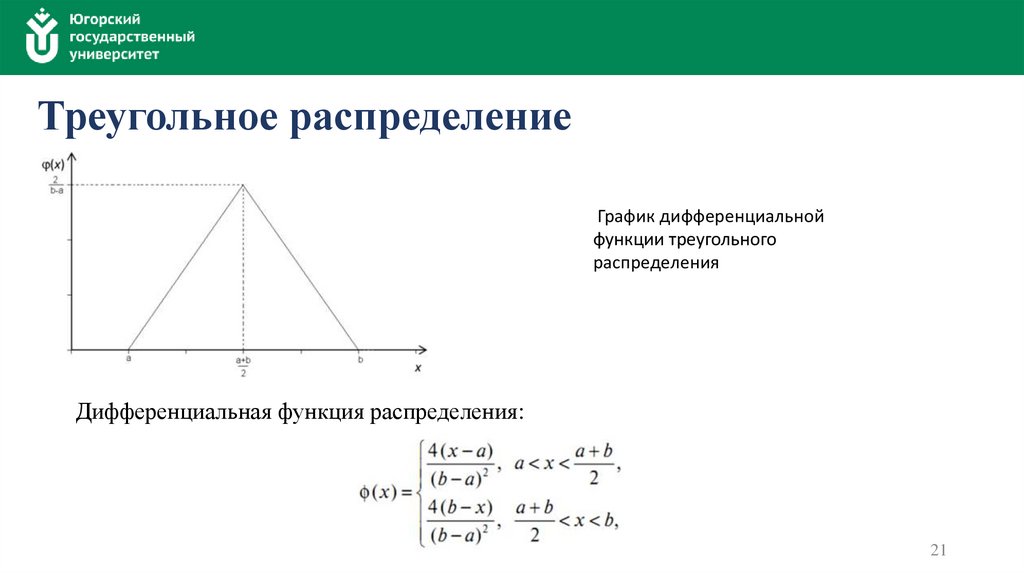
Треугольное распределениеГрафик дифференциальной
функции треугольного
распределения
Дифференциальная функция распределения:
21
22.
Определение вида распределения случайныхвеличин
Проверим, выполняется ли нормальный закон распределения для следующих данных:
Гистограммы экспериментального
(ряд 1) и теоретического (ряд 2)
распределения данных
22
23.
Расчеты:Рассчитываем критерий Пирсона:
значит, распределение экспериментальных данных не противоречит нормальному закону.
Проверка гипотезы:
Критерий I
На основании полученных результатов измерений вычисляют величину dx:
Если
, то вид распределения не противоречит нормальному.
Критерий II
Подсчитывают число результатов m, удовлетворяющих условию:
Если
, то с вероятностью
P2 ≤ 0,98 вид распределения не противоречит нормальному.
23




















 mathematics
mathematics chemistry
chemistry








