Квадратное неравенство

1.

2.

Квадратное неравенство
неравенство вида
ах2 + bх + с > 0
(ах2 + bх + с < 0),
где а, b, с – числа, а ≠ 0.

3.

1) Найти корни квадратного
трехчлена ах2 + bх + с
2) Отметить полученные корни на
оси х
3) Определить направление ветвей
параболы у = ах2 + bх + с
4) Сделать набросок параболы
5) Определить, на каких
промежутках оси х у>0 ( у<0 )
6) Включить эти промежутки в ответ

4.

х2 – 2х – 3 ≥ 0
х2 – 2х – 3 = 0
Находим корни:
х1 = 3; х2 = - 1
-1
Т.к. а = 1, а > 0, то ветви
параболы направлены
вверх.
Ответ: (- ∞; -1] U [ 3; + ∞)
3
х

5.

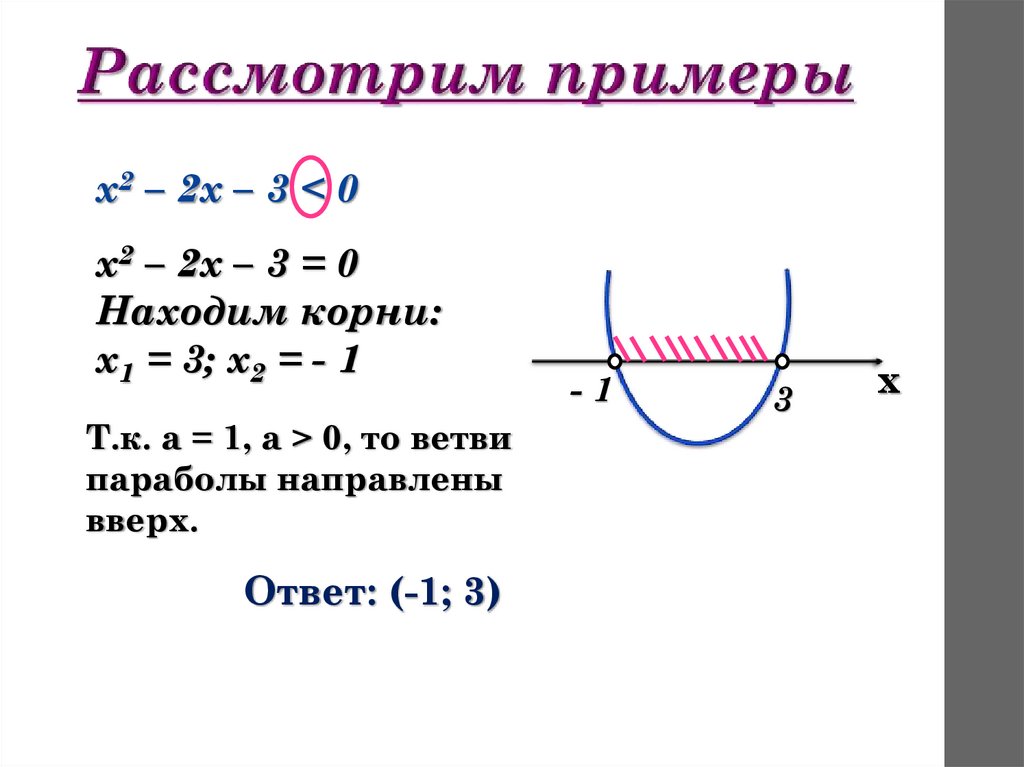
х2 – 2х – 3 < 0
х2 – 2х – 3 = 0
Находим корни:
х1 = 3; х2 = - 1
Т.к. а = 1, а > 0, то ветви
параболы направлены
вверх.
Ответ: (-1; 3)
-1
3
х

6.

-2х2 + 3х + 9 < 0
-2х2 + 3х + 9 = 0
Находим корни:
х1 = 3; х2 = - 1,5
- 1,5
Т.к. а = - 2, а < 0, то ветви
параболы направлены
вниз.
Ответ: (- ∞; -1,5) U (3; + ∞)
3
х

7.

-2х2 + 3х + 9 < 0
Это неравенство можно переписать в виде:
2х2 - 3х - 9 > 0
2х2 - 3х - 9 = 0
Находим корни:
х1 = 3; х2 = - 1,5
- 1,5
3
х
Т.к. а = 2, а > 0, то ветви
параболы направлены
вверх.
Ответ: (- ∞; -1,5) U (3; + ∞)

8.

4х2 – 4х + 1 ≥ 0
4х2 – 4х + 1 = 0
(2х – 1)2 = 0
Находим корни:
х = 0,5
0,5
Т.к. а = 4, а > 0, то ветви
параболы направлены
вверх.
Ответ: (- ∞; + ∞)
х

9.

4х2 – 4х + 1 ≤ 0
4х2 – 4х + 1 = 0
(2х – 1)2 = 0
Находим корни:
х = 0,5
Т.к. а = 4, а > 0, то ветви
параболы направлены
вверх.
Ответ: 0,5
0,5
х

10.

Если квадратный трехчлен ах2 + bх + с не
имеет корней ( D < 0 ) и если при этом
а > 0, то при всех значениях х
выполняется неравенство ах2 + bх + с > 0.
Пример:
2х2 – х + 4 > 0
D = 1 – 32 < 0, а = 2 > 0,
Значит, 2х2 – х + 4 > 0
при любом значении х.
2х2 – х + 4 < 0
D = 1 – 32 < 0, а = 2 > 0,
Значит, нет таких
значений х, при
которых 2х2 – х + 4 < 0
ОТВЕТ: ( - ∞; + ∞)
ОТВЕТ: нет решений

11.

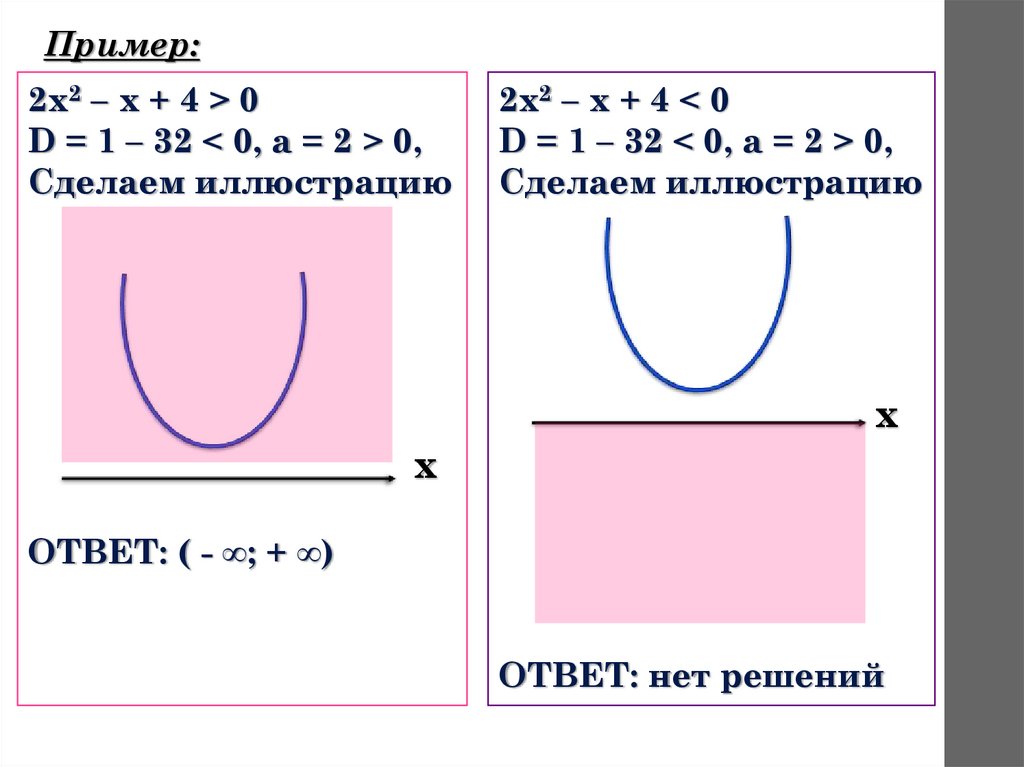
Пример:
2х2 – х + 4 > 0
D = 1 – 32 < 0, а = 2 > 0,
Сделаем иллюстрацию
2х2 – х + 4 < 0
D = 1 – 32 < 0, а = 2 > 0,
Сделаем иллюстрацию
х
х
ОТВЕТ: ( - ∞; + ∞)
ОТВЕТ: нет решений

12.

Если квадратный трехчлен ах2 + bх + с не
имеет корней ( D < 0 ) и если при этом
а < 0, то при всех значениях х
выполняется неравенство ах2 + bх + с < 0.
Пример:
- х2 + 3х – 8 ≤ 0
D = 9 – 32 < 0, а = - 1 < 0,
Значит, - х2 + 3х – 8 ≤ 0
при любом значении х.
- х2 + 3х – 8 ≥ 0
D = 9 – 32 < 0, а = - 1 < 0,
Значит, нет таких
значений х, при
которых - х2 + 3х – 8 ≥ 0
ОТВЕТ: ( - ∞; + ∞)
ОТВЕТ: нет решений

13.

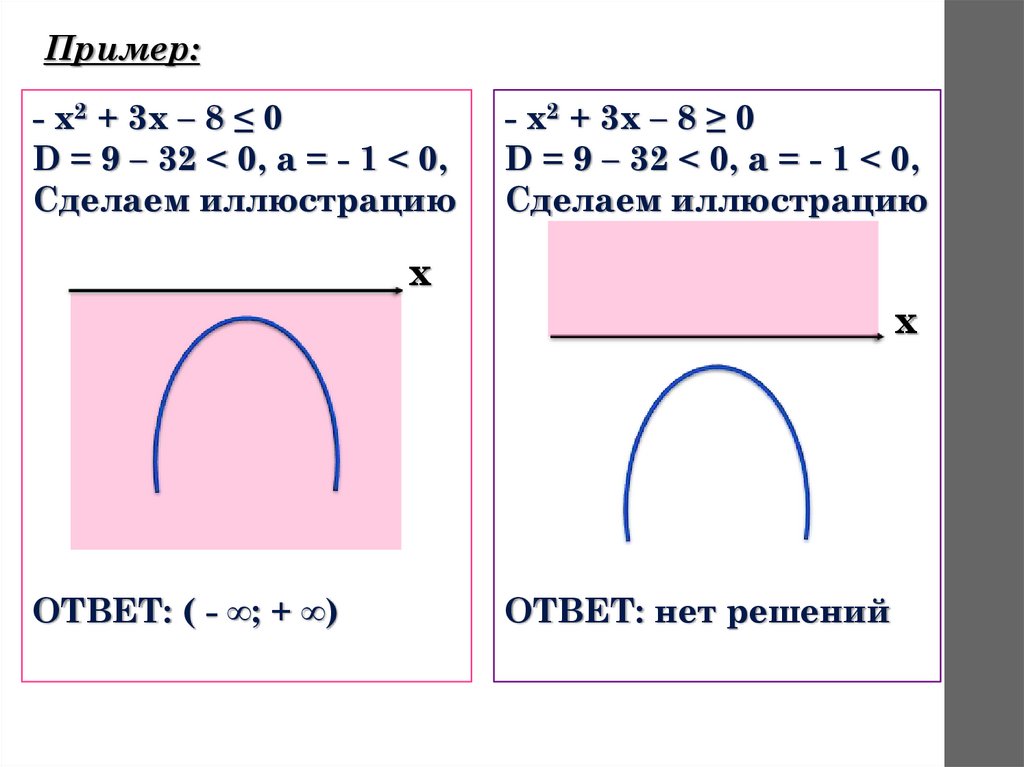
Пример:
- х2 + 3х – 8 ≤ 0
D = 9 – 32 < 0, а = - 1 < 0,
Сделаем иллюстрацию
- х2 + 3х – 8 ≥ 0
D = 9 – 32 < 0, а = - 1 < 0,
Сделаем иллюстрацию
х
х
ОТВЕТ: ( - ∞; + ∞)
ОТВЕТ: нет решений

14.

https://youtu.be/jq7G19g_5q0
https://youtu.be/GNOhXGEJBos
https://youtu.be/dWoe3uPhqtw
https://youtu.be/WsYfFRCgrPw

15.

37.5, 37.7, 37.9, 37.10