Методика изучения геометрических величин. Лекция №6

1. Лекция №6

МЕТОДИКА ИЗУЧЕНИЯ
ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН

2. План

1. Роль изучения величин в школьном курсе
математики. Общее понятие величины.
2. Понятие геометрической величины.
3. Требования программы.
4. Проблема измерения величин.
5. Виды величин. Аксиоматика.
6. Этапы изучения.

3. Роль изучения величин в школьном курсе математики

Математика позволяет изучать и описывать
явления окружающего мира.
Количественные модели того или иного
процесса являются наиболее адекватными.
Характерным общим понятием всех таких
моделей является понятие «величина».
Проблема изучения величин в школе
выделена в одну из основных содержательнометодических линий курса геометрии
основной школы.

4. Понятие величины

Понятие величины - одно из
общенаучных понятий.
важнейших
В физике величины – скорость, сопротивление,
в математике – длина, площадь, объем;
в информатике – объем информации;
в экономике
себестоимость;
–
затраты,
выручка,
прибыль,
в технике – производительность, расход топлива;
в географии – объем осадков, атмосферное давление;
в химии – молярная масса, молярный объем;
в психологии – коэффициент интеллекта и др.

5. Понятие величины

В словаре С.И. Ожегова: «Величина то
(предмет, явление и т.п.), что можно
измерить, исчислить».
А.Н. Крылов писал: «Надо помнить, что
есть множество «величин», то есть того, к
чему приложены понятия «больше» и
«меньше», но величин точно не
измеряемых, например ум и глупость;
красота и безобразие; храбрость и трусость;
находчивость и тупость и т.д.; для
измерения этих величин нет единиц, эти
величины не могут быть числами».

6. Понятие величины

Общее понятие величины – непосредственное
обобщение конкретных величин.
Интуитивно: величина может быть больше или
меньше, две однородные величины могут
складываться, величину можно делить на
произвольное натуральное число, ее можно
измерить (сравнить с другой величиной того же
рода, принятой за единицу измерения).
Однако сформулировать ответ на вопрос, что такое
величина в математических терминах непросто и в
рамках обязательной программы школьное
обучение не должно давать ответ на это вопрос.
В обучении имеют дело с конкретными величинами.

7. Замечание

Позже описательно будут перечислены
аксиомы – свойства общего понятия
величины и отдельно представлены
четыре аксиомы меры величины,
которые возникают в связи с
измерением величин.

8. Величина в геометрии

Понятие величины устанавливает
взаимосвязи между важнейшими
математическими понятиями - числом и
фигурой. При этом:
Величина позволяет перейти от
качественного описательного к
количественному изучению свойств объектов,
то есть математизировать знания об
изучаемом объекте;
Количественное описание – величина –
представляется не только числом, но и
обязательно единицей измерения.

9. Величины в геометрии основной школы

В курсе геометрии основной школы
изучаются
следующие
геометрические
величины:
длина отрезка,
величина угла,
длина окружности,
длина дуги,
площади многоугольника и его частных
видов
(прямоугольника,
треугольника,
параллелограмма, трапеции),
площадь круга.

10. Замечание

В большинстве школьных учебников не
делается различия между понятием
конкретной величины (например, «длина»)
и ее числовым значением, полученным после
измерения.
Поэтому каждое из понятий «длина»,
«площадь», «объем» определяется как
вещественное число, удовлетворяющее
аксиомам меры.

11. Требования программы

Требования к подготовке учащихся,
касающейся изучения и измерения величин в
основной школе:
Ученик должен владеть практическими
навыками использования геометрических
инструментов для изображения фигур, а также
для нахождения длин отрезков и величин
углов;
Решать задачи на вычисление
геометрических величин (длин, углов,
площадей), применяя изученные свойства
фигур и формулы, приводя аргументацию в
ходе решения задачи.

12. Проблема измерения величин

Два основных вопроса:
1) что такое величина (длина, площадь и др.)
- формально-логическая сторона проблемы;
2) с помощью каких инструментов
измеряется величина; по какому закону,
правилу, формуле вычисляется числовое
значение этой величины - прикладная
сторона проблемы.
В школе основной упор делается на прикладную
сторону; ученики имеют дело с конкретными
величинами, иллюстрирующими общее понятие
величины. Для профильных специализированных
классов важен и формально-логический аспект
проблемы.

13. Виды величин. Аксиоматика

Определенные классы величин (класс
скалярных величин, класс векторных
величин и др.) имеют чаще всего
аксиоматическое определение.
Система скалярных величин задается
аксиоматически следующими свойствами:
сравнимостью, аддитивностью,
упорядоченностью, коммутативностью и
ассоциативностью относительно сложения,
монотонностью, существованием разности,
возможностью измерения.

14. Замечание

Эти свойства в явном виде не
формулируются в школе, но выявляются в
ходе решения практических задач
непосредственно при работе с моделями либо
с числовыми значениями величин.

15. Аксиомы меры

Свойства величин, которые проявляются в процессе
измерения, описываются с помощью аксиом меры:
- нормируемости: существование фигуры с мерой,
равной единице;
- неотрицательности: каждой фигуре ставится в
соответствие неотрицательное число;
- инвариантности: равные фигуры имеют равные
меры;
- аддитивности: мера фигуры, составленной из
конечного числа непересекающихся фигур, равна
сумме мер этих фигур.
В курсе геометрии основной школы свойства,
выражающие математическую сущность аксиом
меры, должны быть известны учащимся. Они в
явном или неявном виде находят применение при
изучении конкретных геометрических величин.

16. Замечание

В обучении допускается для упрощения
языка отождествление меры величины с
самой величиной (меры длины с длиной,
меры площади с площадью, меры объема с
объемом).
Поэтому говорят «длина отрезка –
действительное число» вместо «мера длины
отрезка…»
В качестве основных этапов изучения
величин можно выделить пропедевтический
и систематический этапы.

17. Этапы изучения

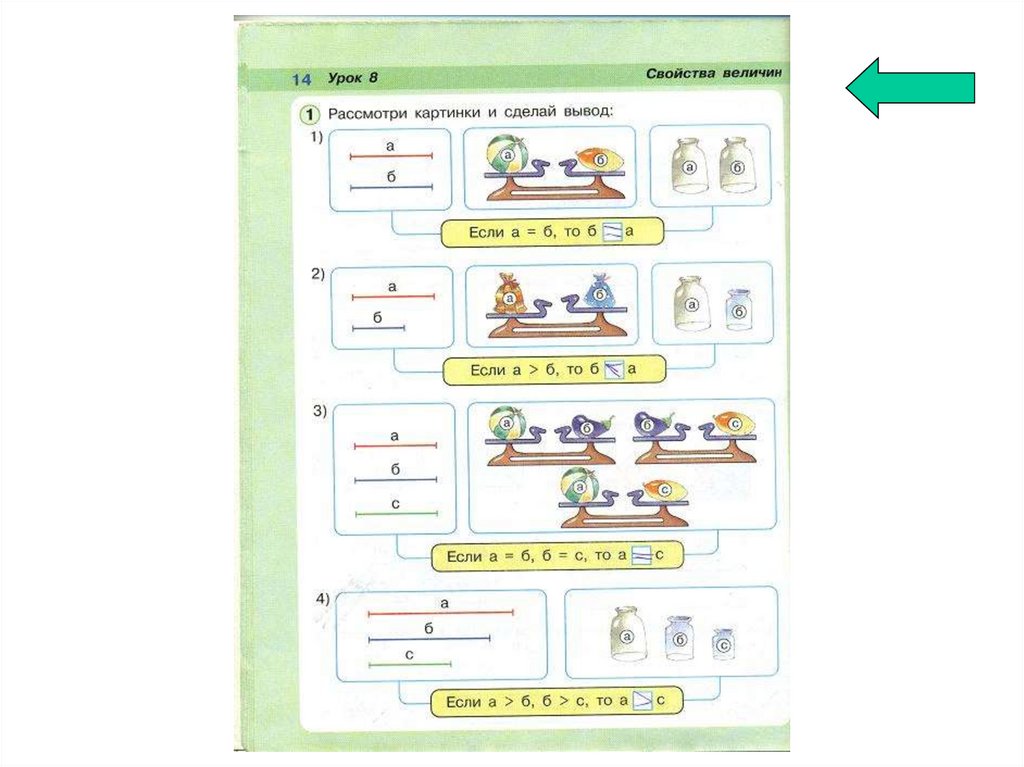
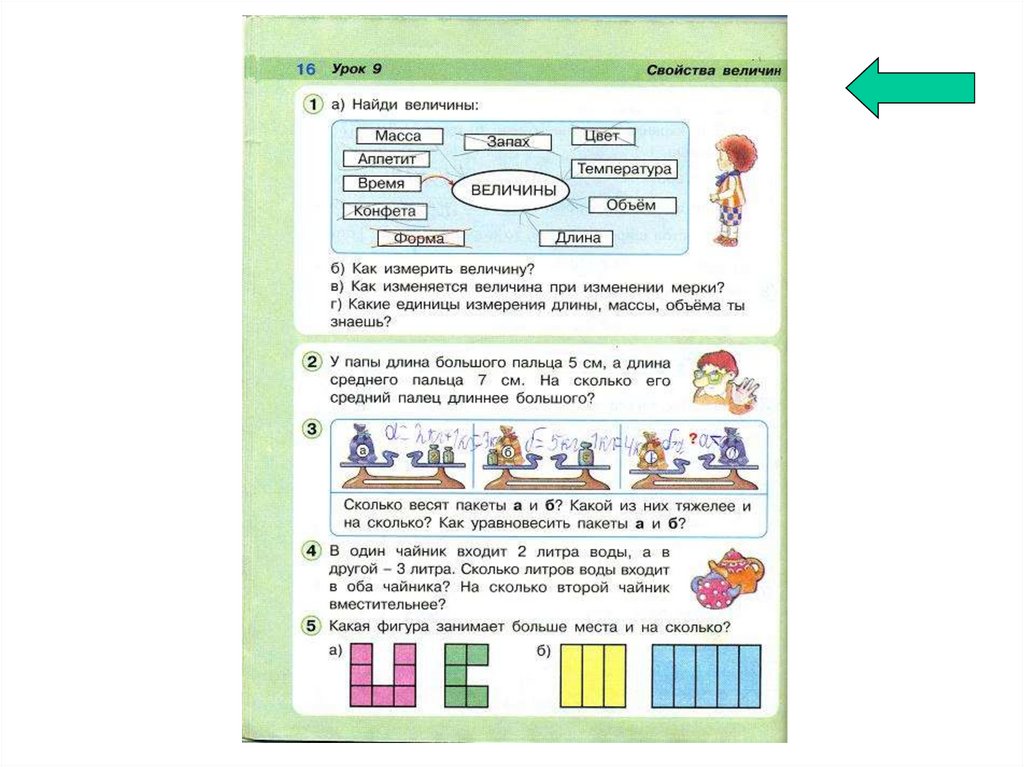
Пропедевтический этап - курс математики 1-6-х
классов.
Развитие интуитивных представлений о
величинах и их практическом измерении:
непосредственное измерение длин отрезков,
взвешивание, определение объема переливанием,
температуры, измерение величин углов с
помощью транспортира и др.
Таким образом, учащиеся усваивают, что для
величин существуют отношения равенства и
неравенства, их можно складывать, делить на
доли, измерять. То есть на интуитивном уровне
отрабатываются свойства величины.

18. Пропедевтический этап

Шаги формирования представлений
учащихся о величинах:
1. Выяснение и уточнение представлений
школьника о данной величине (обращение
к опыту ребенка).
2. Сравнение однородных величин
(визуально, наложением, приложением,
путем использования различных мерок).
3. Знакомство с единицей измерения
данной величины и с измерительным
прибором.
4. Формирование измерительных умений и
навыков.

19. Пропедевтический этап

5. Сложение и вычитание однородных
величин, выраженных в единицах одного
наименования.
6. Знакомство с новыми единицами
измерения величин, перевод однородных
величин в другие, выраженные в других
единицах измерения.
7. Сложение и вычитание величин,
выраженных в единицах двух наименований.
8.
Умножение и деление величин на число.

20. Пропедевтический этап

Расширение объема геометрических знаний
учащихся связано с понятием угла и с
задачей измерения величин углов.
Введение понятия угла: его необходимо
мыслить сразу неограниченным, величина
угла не зависит от «длины сторон» угла.
Учащиеся приходят к мысли о величине
угла и специальном инструменте для ее
измерения (транспортире).
Терминологическая трудность:
специального термина для обозначения
величины угла не существует.

21. Систематический этап

Систематический этап изучения величин
относится к курсу геометрии основной
школы.
Этап изучения методов косвенного
измерения величин.
Требования к учащемуся:
достаточно отчетливое представление о
сущности процесса измерения, о тесной
связи понятия величины с понятием числа.
Знание факта, что числа в своем
историческом развитии возникли в
результате двух основных операций: счета
предметов и измерения величин.

22. Сущность процесса измерения

Измерить величину – это значит, сравнить ее
с другой, однородной величиной, принятой за
единицу измерения.
Этапы процесса измерения величин:
- Из данного рода величин выбирается
некоторая величина, которую называют
единицей измерения
- Осуществляется процесс измерения –
сравнение данной величины с выбранной
единицей измерения.
В результате измерения величины находят
некоторое число – числовое значение данной
величины при выбранной единице
измерения.

23. Отличия

Следует четко различать геометрическую фигуру,
величину, относящуюся к фигуре и числовое
значение этой величины.
Геометрическая
фигура
Величина
Значение
величины
1. Отрезок АВ
Длина отрезка АВ
Числовое значение
длины отрезка АВ
Обозначение:
[АВ]
Обозначение:
|AB|=4см
4
2. Угол АВС
Величина
АВС
Обозначение:
АВС
Обозначение:
АВС=60
угла
Числовое значение
величины
угла
АВС
60

24. Систематический этап

Развиваются знания и навыки, связанные с
прикладной стороной вопроса:
изучаются факты, позволяющие от
измерений перейти к вычислению величин с
помощью формул;
основное внимание здесь уделяется
вычислению по формулам площадей фигур.
Отражение получает и формальнологическая сторона вопроса: изучаются
основные свойства длин и площадей аналоги аксиом меры.

25. История

Первые единицы длины, как на Руси, так и у других
народов древности, были связаны с различными
частями тела человека: ширина ладони – 1 ладонь, 7
ладоней – 1 локоть, длина первой фаланги большого
пальца руки – 1 дюйм, расстояние между концами
пальцев разведенных в стороны рук – маховая
сажень, расстояние от пальцев левой ноги до конца
пальцев поднятой правой руки - косая сажень.
- «Локоть» – мера длины, которой купцы
пользовались для измерения ткани, египтяне
измеряли локтями подъем Нила;
- «ладонями» английские крестьяне измеряли
высоту лошадей;
- «дюйм» - голландское название. Эта мера
использовалась для измерения небольших предметов
(вспомнить сказку Г.Х.Андерсена «Дюймовочка»).

26. История

Также известны другие единицы измерения: ярд
(этой мере длины 900 лет. Она была равна
расстоянию от конца носа короля Генриха I до
конца пальцев его вытянутой руки). Один ярд равен
трем футам, фут – «ступня», равен 12 дюймам и
др.
Измерения давали разные результаты, потому что
у всех людей разные по размеру руки. Это заметил
английский король Эдуард II, который установил
«законный дюйм, равный длине трех ячменных
зерен, выложенных в ряд». В Россию дюйм пришел в
царствование Петра I. Он равен 2см 5мм.

27. История

У нас сейчас принята система измерений длины, в
основе которой лежит метр и его доли –
метрическая система. Ее создали французы. В
1792г. Академия наук измеряла длину земного
меридиана, проходящего через Париж. В результате
огромной работы была найдена длина парижского
меридиана в «туазах». Парижская Академия наук
предложила принять за единую меру длины новую
единицу измерения – «метр», равную одной
десятимиллионной доле четверти парижского
меридиана. В России первым применил метр как
единицу длины Н.И. Лобачевский. Инициаторами
введения метрической системы мер как
международной были русские ученые и, главным
образом, Б.С. Якоби. Обязательной в нашей стране
эта система стала после 1918г.

28. История

В основной школе, после ознакомления с
иррациональными числами, рассказ о проблеме
соизмеримости величин.
Подобно тому, как единица была общей мерой
целых чисел, величины должны иметь общую
единицу измерения – быть соизмеримыми, каждая
величина отождествлялась с целым числом
составляющих ее единиц. Эта попытка
отождествить целые числа с непрерывными
величинами ни к чему не привела. Решающую роль
в этом сыграло открытие пифагорейцами
иррационального числа. В квадрате со стороной 1
отношение диагонали к стороне равно 2; оно не
выражалось в виде отношения целых чисел.
Сторона и диагональ не имеют общей единицы
измерения и называются несоизмеримыми. В связи
с открытием несоизмеримых величин в греческую
математику проникло понятие бесконечности.