Similar presentations:
Построение таблиц истинности для сложных высказываний
1.
Построение таблиц истинностидля сложных высказываний
2.
Порядок логических операций1.
2.
3.
4.
Инверсия
Конъюнкция
Дизъюнкция
Импликация и эквивалентность
3.
Пример 1В классе оказалось разбито стекло. Учитель
объясняет директору: Это сделал Коля или
Саша. Но Саша этого не делал, так как в
это время сдавал мне зачет.
Следовательно, это сделал Коля.
Прав ли учитель?
К = Это сделал Коля
С = Это сделал Саша
4.
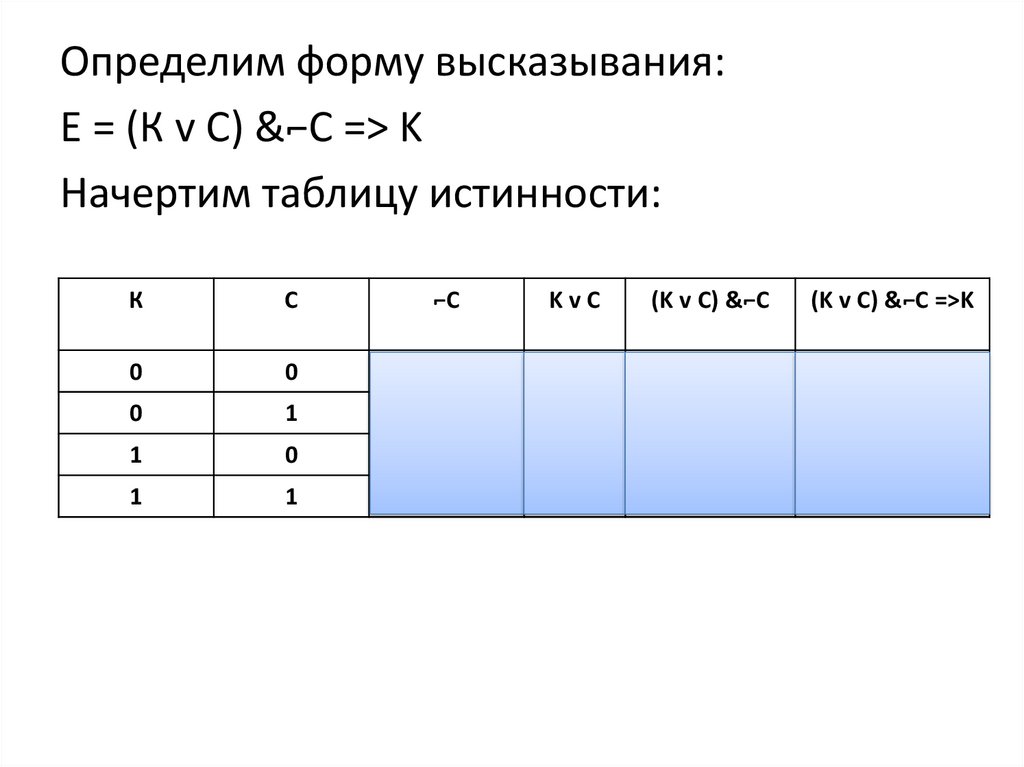
Определим форму высказывания:Е = (К v C) &⌐C => K
Начертим таблицу истинности:
К
С
⌐С
KvC
(K v C) &⌐C
(K v C) &⌐C =>K
0
0
1
0
0
1
0
1
0
1
0
1
1
0
1
1
1
1
1
1
0
1
0
1
5.
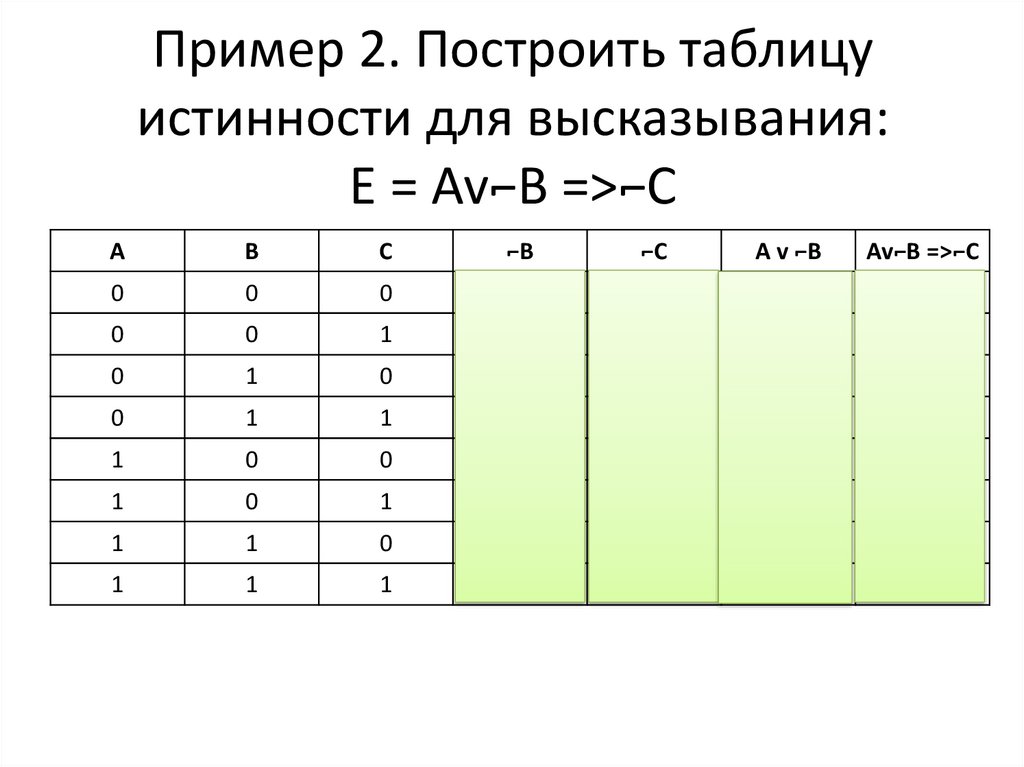
Пример 2. Построить таблицуистинности для высказывания:
Е = Av⌐B =>⌐C
A
B
C
⌐B
⌐C
A v ⌐B
Av⌐B =>⌐C
0
0
0
1
1
1
1
0
0
1
1
0
1
0
0
1
0
0
1
0
1
0
1
1
0
0
0
1
1
0
0
1
1
1
1
1
0
1
1
0
1
0
1
1
0
0
1
1
1
1
1
1
0
0
1
0
6.
Если высказывание истинно при всех значениях входящих внего переменных, то такое высказывание называется
тождественно истинным или тавтологией.
Пример: Дождь будет или дождя не будет.
Av⌐A
7.
Если высказывание ложно при всех значениях входящих в негопеременных, то такое высказывание называется
тождественно ложным.
Пример: Сегодня среда, а это второй день недели.
A&⌐A
8.
Если значения сложных высказываний совпадают на всехвозможных наборах значений входящих в них переменных, то
такие высказывания называют равносильными, или
тождественными, или эквивалентными.
Пример:
X = Не может быть, что Матроскин выиграл приз и отказался
от него.
X = ⌐ (A & B)
Y = Или Матроскин не отказался от приза, или не выиграл его.
Y = ⌐A v ⌐B
9.
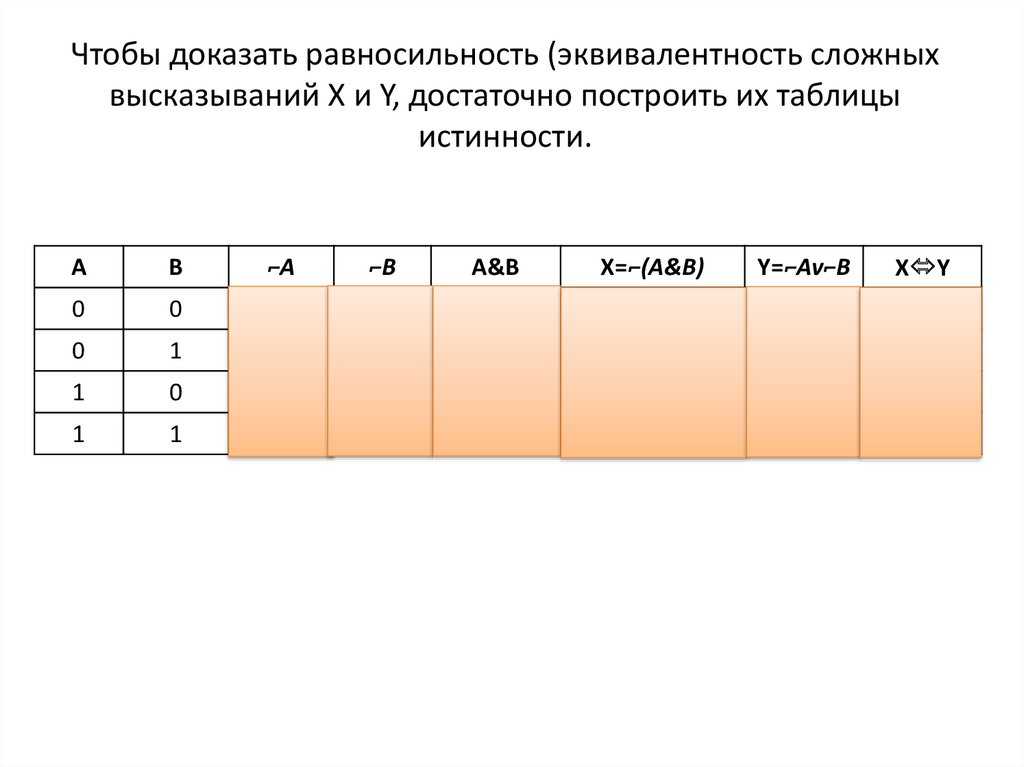
Чтобы доказать равносильность (эквивалентность сложныхвысказываний X и Y, достаточно построить их таблицы
истинности.
A
B
⌐A
⌐B
A&B
X=⌐(A&B)
Y=⌐Av⌐B
X Y
0
0
1
1
0
1
1
1
0
1
1
0
0
1
1
1
1
0
0
1
0
1
1
1
1
1
0
0
1
0
0
1






 informatics
informatics








