Построение таблиц истинности для логических выражений

1.

Построение таблиц
истинности для
логических выражений

2. повторить

ПОВТОРИТЬ
Что такое высказывание? Приведите примеры.
2. Какие логические операции вы знаете?
3. Что такое конъюнкция и с помощью каких
знаков она записывается?
4. Что такое дизъюнкция и как она записывается?
5. Какая
логическая
операция
называется
инверсией и какие знаки используются для ее
обозначения?
6. Каков
приоритет выполнения логических
операций?
1.

3.

Что такое таблицы
истинности и для чего они
необходимы?

4. Записать в тетрадь

ЗАПИСАТЬ В ТЕТРАДЬ
Таблица истинности - это такая
таблица, в которой показываются все
выходные состояния элемента для
любых комбинации входных сигналов.
Иными словами, с помощью таблиц
истинности
можно
определять
истинностное
значение
любого
высказывания для всех возможных
случаев
значений
истинности
составляющих его высказываний.

5.

Построить
таблицу
истинности,
описывающую
работу
логических
элементов, несложно при небольшом
количестве входных переменных. Если же
число переменных больше трех, то таблица
получается слишком большой. Так, при
наличии 4 переменных, количество наборов
в таблице будет равно 16, а уже при 6
переменных - 64! А еще нужно учитывать
скобки, приоритет и количество операций!
Очень легко совершить ошибку!

6.

Записать в тетрадь
Алгоритм построения таблиц истинности
1. Подсчитать n — число переменных в логическом выражении.
2. Подсчитать общее количество логических операций в выражении.
3. Установить последовательность выполнения логических операций
с учётом скобок и приоритетов.
4. Определить число столбцов в таблице: число переменных + число
операций.
5. Заполнить шапку таблицы, включив в неё переменные и операции
в соответствии с последовательностью, установленной в пункте 3.
6. Определить число строк в таблице (не считая шапки таблицы) по
формуле
m = 2n, где n — количество переменных.
7. Выписать наборы входных переменных с учётом того, что они
представляют собой целый ряд n-разрядных двоичных чисел от 0 до
2n–1.
8. Провести заполнение таблицы истинности по столбцам, выполняя
логические
операции
в
соответствии
с
установленной
последовательностью.

7.

Записать в тетрадь
Пример построения таблицы истинности
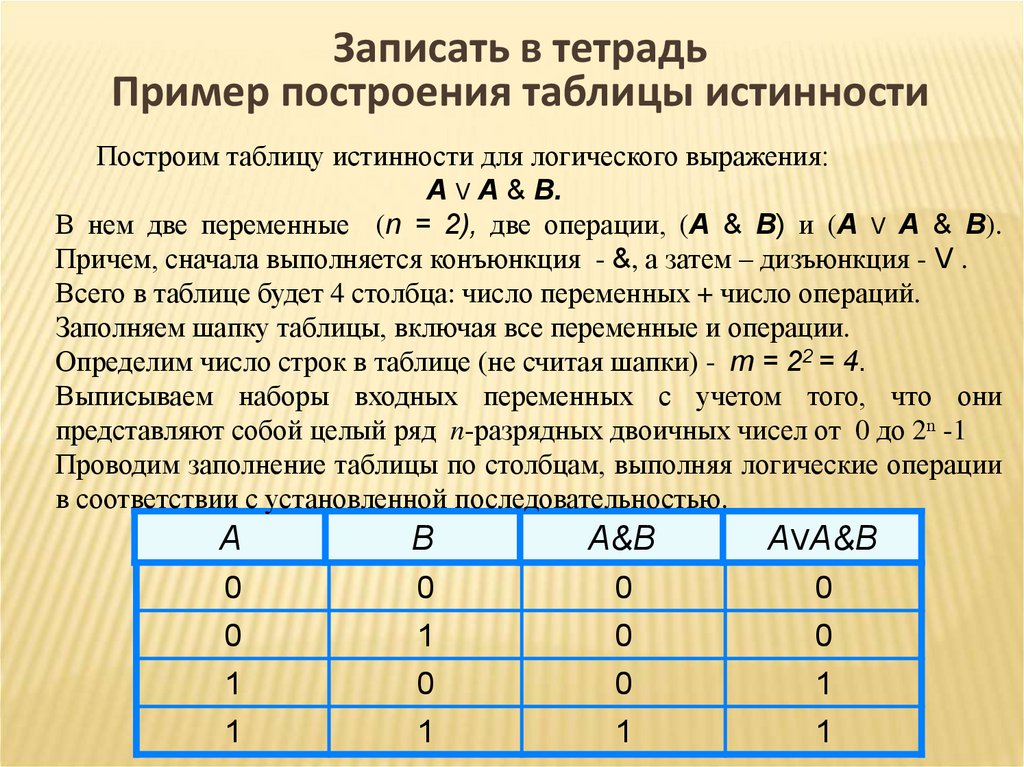
Построим таблицу истинности для логического выражения:
А V A & B.
В нем две переменные (n = 2), две операции, (A & B) и (А V A & B).
Причем, сначала выполняется конъюнкция - &, а затем – дизъюнкция - V .
Всего в таблице будет 4 столбца: число переменных + число операций.
Заполняем шапку таблицы, включая все переменные и операции.
Определим число строк в таблице (не считая шапки) - m = 22 = 4.
Выписываем наборы входных переменных с учетом того, что они
представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2ⁿ -1
Проводим заполнение таблицы по столбцам, выполняя логические операции
в соответствии с установленной последовательностью.
A
B
A&B
AVA&B
0
0
0
0
0
1
0
0
1
0
0
1
1
1
1
1

8.

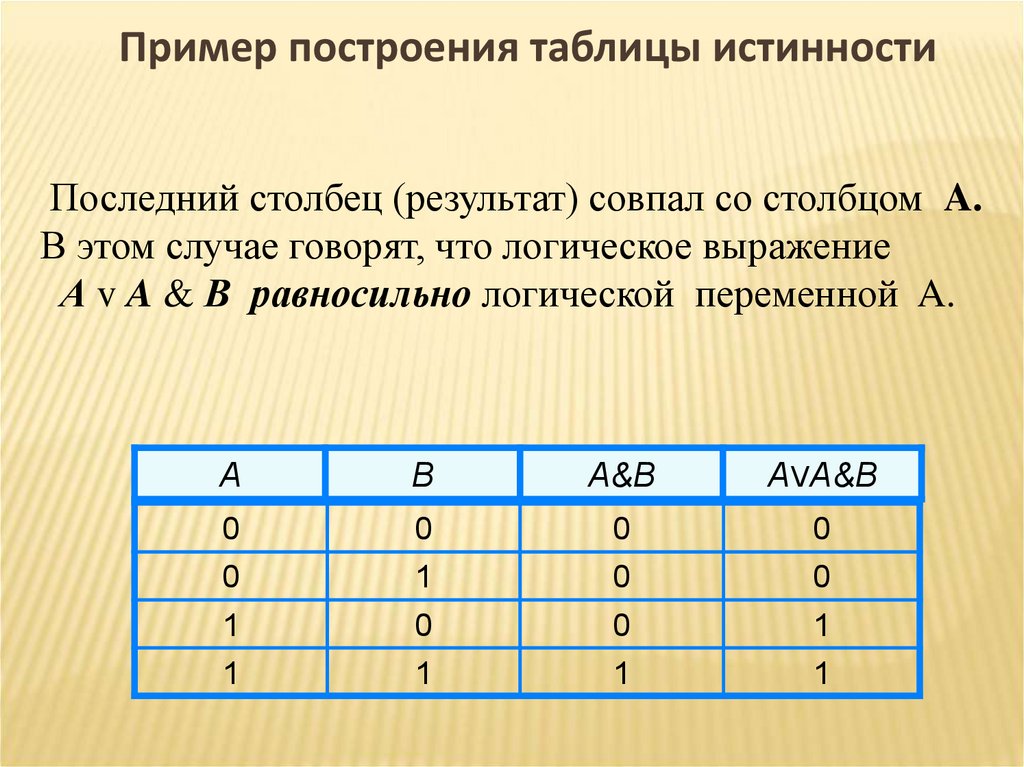
Пример построения таблицы истинности
Последний столбец (результат) совпал со столбцом A.
В этом случае говорят, что логическое выражение
А v A & B равносильно логической переменной A.
A
B
A&B
AVA&B
0
0
0
0
0
1
0
0
1
0
0
1
1
1
1
1

9.

Для формулы A /\ (B v ¬ B /\ ¬ C)
постройте таблицу истинности
1.
2.
A
B
A /\ (B v ¬ B /\ ¬ C)
5
3.
C
4
1
3
Количество логических операций в формуле: 5.
2
A /\ (B v ¬ B /\ ¬ C)
4. Количество столбцов: 3+5=8
5. Количество строк: 8+1 = 9

10.

Для формулы A /\ (B v ¬ B /\ ¬ C) постройте таблицу истинности

11.

Построить таблицу истинности
F= (А \/ В) /\ (¬А \/¬В)
А
В
А\/ В
¬А
¬В
¬А\/¬В
(А\/
В)/\(¬А\/¬В)
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0