Понятие об алгебре высказываний

1.

Понятие об алгебре
высказываний

2.

Идею о возможности математизации логики
высказал еще в XVII веке немецкий
математик Готфрид Лейбниц. Он пытался
создать универсальный язык, с помощью
которого каждому понятию и суждению
можно было бы дать числовую
характеристику и установить правила
оперирования этими числами, которые
позволили бы сразу определить, истинно
данное высказывание или ложно.
То есть он предполагал, что споры между
людьми можно будет разрешать
посредством вычислений.

3.

Прогресс науки, называемой
математической логикой, был достигнут в
середине XIXвека благодаря труду
английского ученого Джорджа Буля.
В трудах Дж. Буля и О. де Моргана
математическая логика представлена как
своеобразная алгебра – алгебра
высказываний.

4.

Алгебра логики (алгебра высказываний) –
раздел математической логики, изучающий
строение (форму, структуру) сложных
логических высказываний и способы
установления их истинности с помощью
алгебраических методов.

5.

Под высказыванием будем понимать
повествовательное
предложение,
относительно которого можно сказать,
истинно оно или ложно.
Обозначать высказывания будем прописными
буквами. Например: Х = Число 12345 кратно 3.
Если высказывание А истинное, то будем писать «А=1».
Если высказывание А ложно, то будем писать «А=0».

6.

Примеры:
А = Солнце светит для всех = 1
В = Все ученики любят информатику = 0
С = Некоторые ученики любят информатику = 1
Д = А ты любишь информатику?
Е = Посмотри в окно
Ж = (х*х<0)
З = 2*х-5>0
не является высказыванием
не является высказыванием
=0
не является высказыванием
И = Крокодилы летают очень низко
высказывание

7.

Последний пример показывает, что
истинность или ложность высказывания
необязательно должна определяться
здравым смыслом. Вопрос о том, летают или
не летают крокодилы, может волновать
зоологов, но никак не логиков, так как им этот
потрясающий факт безразличен.

8.

Логические операции
Логическая операция – способ построения
сложного высказывания из данных
высказываний, при котором значение
истинности сложного высказывания
полностью определяется значениями
истинности исходных выражений.

9.

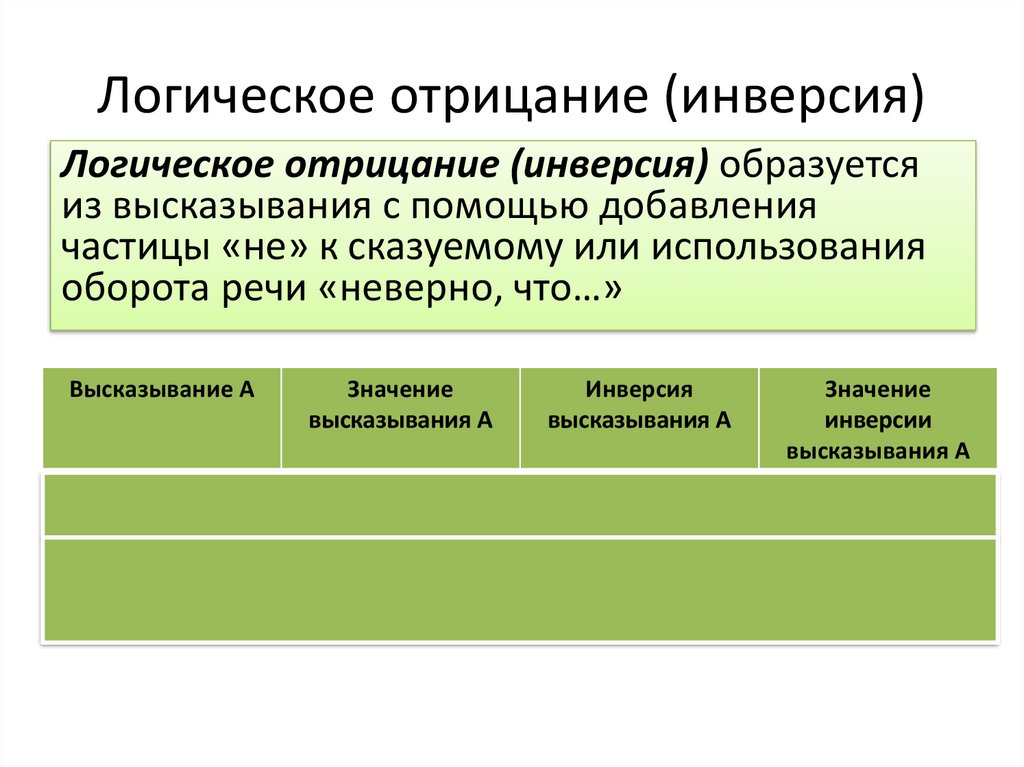
Логическое отрицание (инверсия)
Логическое отрицание (инверсия) образуется
из высказывания с помощью добавления
частицы «не» к сказуемому или использования
оборота речи «неверно, что…»
Высказывание А
Значение
высказывания А
Инверсия
высказывания А
Значение
инверсии
высказывания А
У меня есть
приставка Dendy
0
У меня нет
приставки Dendy
1
Я не знаю
китайского языка
1
Неверно, что я не
знаю китайского
языка
0

10.

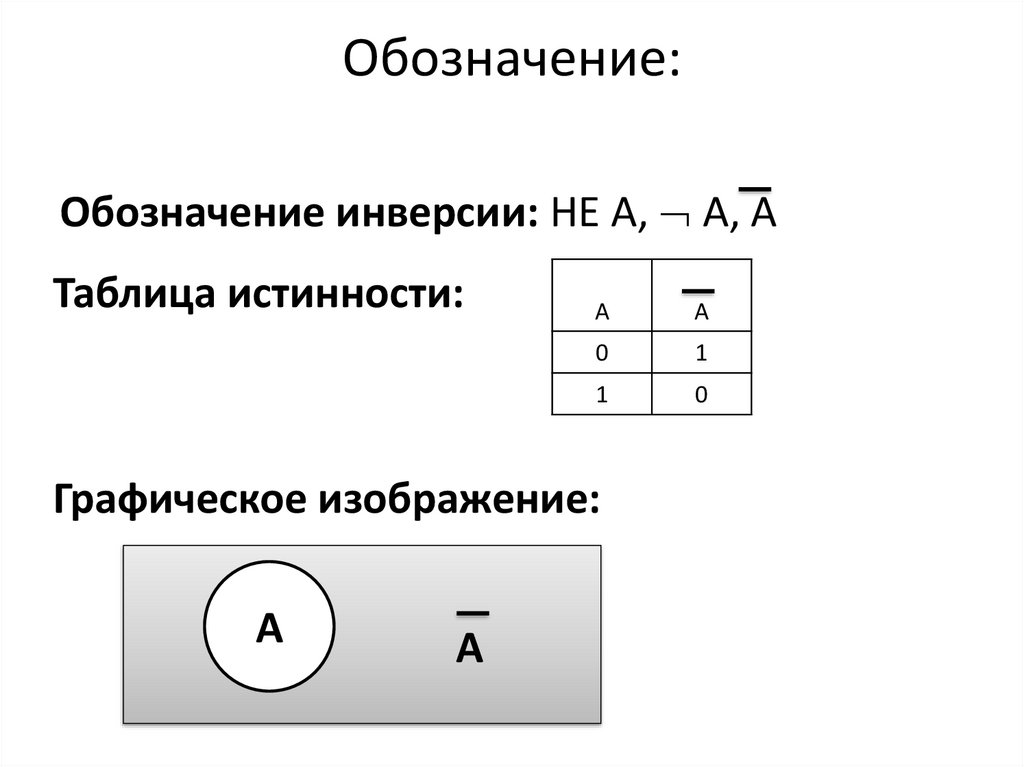
Обозначение:
Обозначение инверсии: НЕ А, А, А
Таблица истинности:
А
А
0
1
1
0
Графическое изображение:
А
А

11.

Примечание
Дважды или четырежды отрицающееся
высказывание имеет то же самое значение
истинности, что и исходное высказывание,
трижды отрицающееся – что и отрицающееся
один раз.
Высказывание
А = Неверно, что математика не царица наук
имеет то же значение истинности, что и высказывание
В = Математика – царица наук.

12.

Инверсия высказывания истинна, когда
высказывание ложно, и ложна, когда
высказывание истинно.

13.

Логическое умножение (конъюнкция)
Логическое умножение (конъюнкция)
образуется соединением двух высказываний
в одно с помощью союза «и».
Пример.
Допустим, из вашего окна видна автостоянка, на которой обычно стоят две
машины: «Мерседес» и «Жигули», но может находиться и одна из них или не быть
ни одной.
Обозначим высказывания:
А = На автостоянке стоит «Мерседес»
В = На автостоянке стоят «Жигули»
(А конъюнкция В) = На автостоянке стоят «Мерседес» и «Жигули».

14.

Обозначение:
А И В;
А^В;
А & В;
А*В;
А and В.
Таблица истинности:
А
В
А&В
0
0
0
0
1
0
1
0
0
1
1
1
Графическое обозначение:
А – множество отличников в
классе
В – множество спортсменов
в классе
А&В – множество
отличников, занимающихся
спортом

15.

Конъюнкция двух высказываний истинна
тогда и только тогда, когда оба
высказывания истинны, и ложна, когда хотя
бы одно высказывание ложно.

16.

Логическое сложение (дизъюнкция)
Логическое сложение (дизъюнкция)
образуется соединением двух высказываний
в одно с помощью союза «или».
Пример.
Допустим, из вашего окна видна автостоянка, на которой обычно стоят две
машины: «Мерседес» и «Жигули», но может находиться и одна из них или не быть
ни одной.
Обозначим высказывания:
А = На автостоянке стоит «Мерседес»
В = На автостоянке стоят «Жигули»
(А дизъюнкция В) = На автостоянке стоят «Мерседес» или «Жигули».

17.

Обозначение:
А или В;
А or В;
А V В;
А I В;
А + В.
Таблица истинности:
А
В
АVВ
0
0
0
0
1
1
1
0
1
1
1
1
Графическое обозначение:
А – множество отличников в
классе
В – множество спортсменов
в классе
АVВ – множество учеников
класса, которые являются
отличниками или
спортсменами

18.

Дизъюнкция двух высказываний ложна
тогда и только тогда, когда оба
высказывания ложны, и истинна, когда хотя
бы одно высказывание истинно.

19.

Логическое следование (импликация)
Логическое следование (импликация)
образуется соединением двух высказываний в
одно с помощью оборота речи «если…, то…».
Примеры.
Е = Если клятва дана, то она должна выполняться.
Р = Если число делится на 9, то оно делится на 3.
В логике допустимо рассматривать и бессмысленные с житейской точки
зрения высказывания.
С = Если коровы летают, то 2 + 2 = 5
Х = Если я - Наполеон, то у кошки четыре ноги.

20.

Обозначение: А => В; А В.
А = На улице дождь.
В = Асфальт мокрый.
Таблица
истинности:
Смысл высказываний А и В
Значение
высказывания
А=>В
А
В
А=>В
0
0
1
Дождя нет
Асфальт сухой
Истина
0
1
1
Дождя нет
Асфальт мокрый
Истина
1
0
0
Дождь идет
Асфальт сухой
Ложь
1
1
1
Дождь идет
Асфальт мокрый
Истина

21.

Дано высказывание:
Если коровы летают, то 2 +2 =5
Форма высказывания:
Если А, то В.
Где
А = Коровы летают = 0
В = (2+2=5) = 0
На основании таблицы истинности
определим значение высказывания:
0=>0 = 1, т.е. высказывание истинно.

22.

Импликация двух высказываний ложна
тогда и только тогда, когда из истинного
высказывания следует ложное.

23.

Логическое равенство (эквивалентность)
Логическое равенство (эквивалентность)
образуется соединением двух высказываний в одно с
помощью оборота речи «…тогда и только тогда,
когда…».
Примеры эквивалентностей:
Угол называется прямым тогда и только тогда, когда он
равен 900
Две прямы параллельны тогда и только тогда, когда они не
пересекаются.
Любая материальная точка сохраняет состояние покоя или
равномерного прямолинейного движения тогда и только
тогда, когда нет внешнего воздействия. (Первый закон
Ньютона)
Голова умеет думать тогда и только тогда, когда язык
отдыхает.

24.

Обозначение: А <=> В; А В, А В.
А = Число делится на 3 без остатка.
В = Сумма цифр числа делится нацело на 3.
(А эквивалентно В) = Число кратно 3 тогда и только тогда, когда
сумма его цифр делится нацело на 3.
Таблица
истинности:
А В
Смысл высказываний А и В
Значение
высказывани
я А <=> В
А<=>В
0
0
1
Число не кратно 3
Сумма цифр не кратна 3
Истина
0
1
0
Число не кратно 3
Сумма цифр кратна 3
Ложь
1
0
0
Число кратно 3
Сумма цифр не кратна 3
Ложь
1
1
1
Число кратно 3
Сумма цифр кратна 3
Истина

25.

Эквивалентность двух высказываний
истинна тогда и только тогда, когда оба
высказывания истинны или оба ложны.