Similar presentations:
Равносильные уравнения
1. Равносильные уравнения
2.
1)Чтоназывается
уравнением?
2)Что такое корень
уравнение?
3) Что значит решить
уравнение?
4)Что называют ОДЗ
уравнения?
3. Найдите ОДЗ следующих уравнений.
1)2)
3)
4)
x2 9 x2 4 6
x 1 x 2 2
( x 1) x 2 2
5 3x
x2 1
5)
6)
5 x
x2 1
5 x
5 x x 17 5 x
10
5 x
x
10
.
5 x
x
4.
12
3
2 x 13 x 1 12 x ,
2
2
x 2 2 x 12 2 x 13 x 2 ,
x 2 2 x 1 13 x 2 2 x 13 x 2 x 2 ,
4 x 1 13 x x ,
5 x 1 13 x 2 x ,
6 2 x 1 13 x 2 ,
2
7 2 x 1 13 x 2 ,
2
x 2,
2
6
x
5
2
5. Цель урока
Выявитьпреобразования над
уравнениями, которые сохраняют
корни, приводят к потере корней
или приобретению посторонних
корней. Знать, какими
преобразованиями их можно
заменить, чтобы потери или
приобретения корней не было
6. Определение
Уравненияf1 x g1 xи f x g x
2
называются
равносильными, если
множества их корней
совпадают.
2
7. Сохраняют равносильность
Раскрытиескобок;
перенос слагаемых из одной
части уравнения в другую,
изменяя знак на
противоположный;
прибавление к обеим частям
уравнения выражения,
содержащее неизвестную
8. Определение равносильного уравнения
Уравнение f 2 x g 2 xназывают
следствием уравнения ,f1 x g1 x
если каждый корень уравнения
f1 x g1 x является корнем
fуравнения
2 x g 2 x
9. Задание 1
а)x2 9 x2 4 6
1
ОДЗ : x R
x 0
x
2
9 x 2 4 6 2
ОДЗ : x R
x 0
б)
x 1 x 2 2
3
ОДЗ : x 2
x 3
x 1 x 2 2 4
x 3, x 2
ОДЗ : x 1; x 2
10. Теорема 1
f x g x1.
а) ОДЗ f x g x не изменяется
Теорема
f x g x f1 x g x
б) ОДЗ f x g x расширяется
f x g x
f1 x g x
11. Задание 2
5 3x x 171
ОДЗ : x R
x 6
5 3x x 2 1 x 17 x 2 1
2
ОДЗ : x R
x 6
5 3x
5 x x 17 5 x
нет корней
3
ОДЗ : x 5
12. Теорема 2
f x g xx
f x g x
на ОДЗ
определена уравнения
f x g x
f x x g x x
13. Задание 3
x2 11
10
5 x
5 x
x 3, x 3
2
x 2 1 10
ОДЗ : x 5
ОДЗ : x R
x 3, x 3
x2 1
x
10
5 x
5 x
x 3, x 3, x 0.
x
3
ОДЗ : x 0
14. Теорема 3
f x g xx
x 0
- определена на всей ОДЗ f x g x
для любого
x
и ОДЗ f x g x
f x g x f x x g x x
15. Решить уравнение
36 x x
1
3
x x 12
4
2
16. Домашнее задание
знать определения равносильныхуравнений, уравнения-следствия;
знать формулировки теорем 1-4;
провести по аналогии с
доказательством теоремы 3
доказательство теорем 1 и 2;
№№ 139(4,6), 141(2) – выяснить,
являются ли уравнения
равносильными



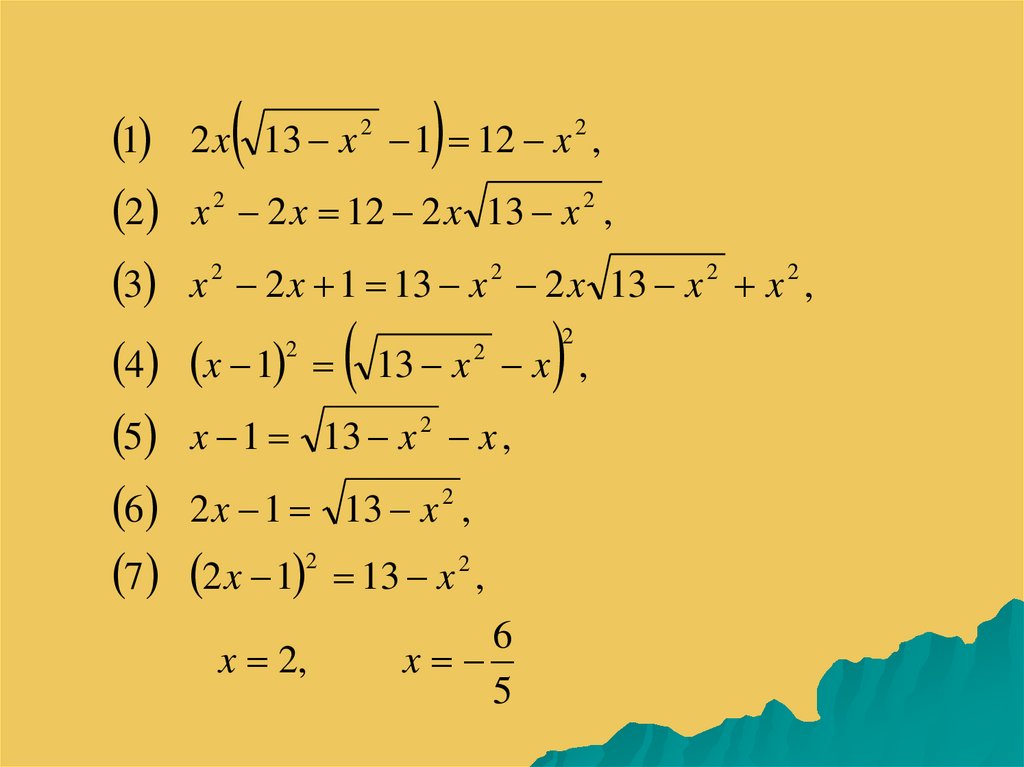













 mathematics
mathematics








