Similar presentations:
Иррациональные уравнения
1.
ИРРАЦИОНАЛЬНЫЕУРАВНЕНИЯ
2. Цель:
познакомиться с понятиемиррационального уравнения и
некоторыми методами их решений
3.
Определение:Уравнения, в которых под знаком
корня содержится переменная,
называются иррациональными.
Например:
2x 3 x 1
3
x 5 12 x 4 5
4.
Основные методы решенияиррациональных уравнений:
возведение в степень обеих частей
уравнения;
введение новой переменной;
разложение на множители.
5.
Метод возведения в степеньобеих частей уравнения:
1) Если иррациональное уравнение
только один радикал,
то нужно
2) содержит
Если в иррациональном
уравнении
записать так,
чтобы
в одной
части знака
содержится
два или
более
радикала,
то
равенства оказался только этот радикал.
сначала изолируется один из радикалов,
Затем
обе части
части уравнения
уравнения возводят
возводят вв одну
одну
затем обе
и ту же степень, чтобы получилась
и ту же степень, и повторяют операцию
рациональное уравнение
возведения в степень до тех пор, пока не
получится рациональное уравнение.
6. Пример 1.
7. Пример 2.
8.
Пример 3.9.
Проверка.10.
Пример 4.11.
Проверка.12.
Пример 5.13.
f ( x) g ( x)f ( x) g ( x)
g ( x) 0
f ( x) g ( x)
f ( x) g ( x)
f ( x ) 0 ( g ( x ) 0)
2
14.
Пример 6.Ответ: 11
15.
Пример 7.16.
Итоги занятияУравнения, в которых переменная содержится под
знаком корня, называются иррациональными.
При возведении обеих частей уравнения
• в четную степень (показатель корня – четное число)
– возможно появление постороннего корня (проверка
необходима).
• в нечетную степень (показатель корня – нечетное
число) – получается уравнение, равносильное
исходному (проверка не нужна).
Решая иррациональные уравнения с помощью
равносильных преобразований – проверка не нужна.












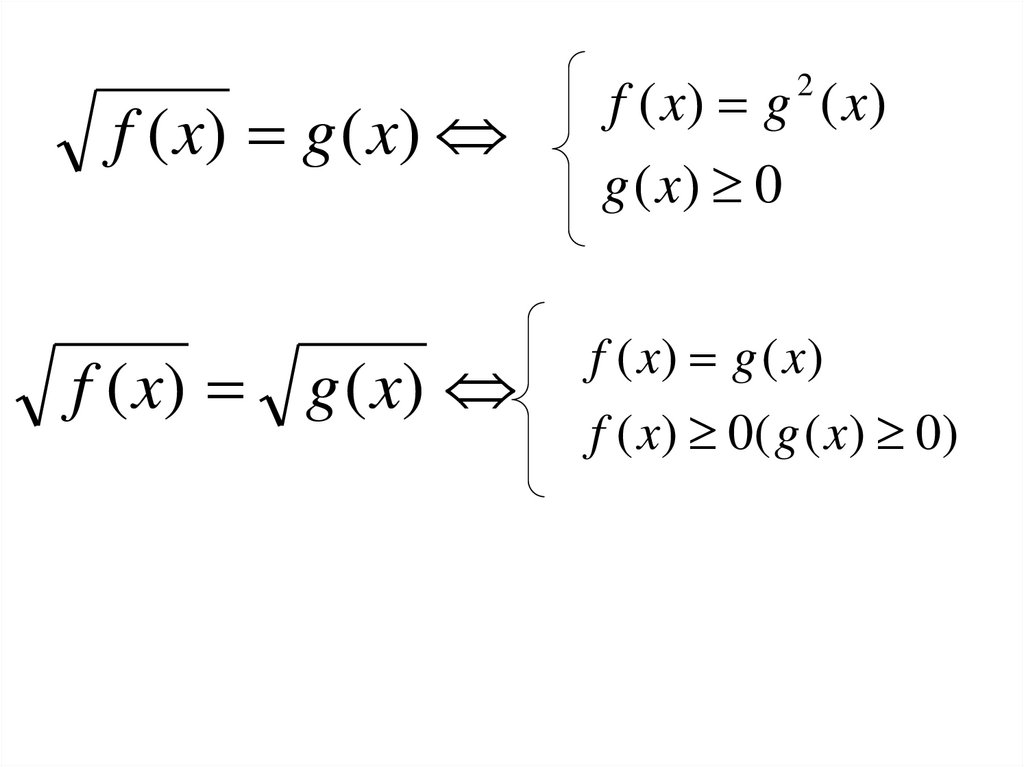



 mathematics
mathematics








