Similar presentations:
DS программирование. Множества
1.
DSпрограммирование
Множества
2.
ВведениеПлан
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
3.
ВведениеПлан
Узнаем что такое множества и как добавлять и удалять данных из
множества
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
4.
ВведениеПлан
Узнаем что такое множества и как добавлять и удалять данных из
множества
Изучим ограничения, связанные с множествами
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
5.
ВведениеПлан
Узнаем что такое множества и как добавлять и удалять данных из
множества
Изучим ограничения, связанные с множествами
Узнаем об операциях: пересечение, объединение и вычитание
множеств
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
6.
ВведениеПлан
Узнаем что такое множества и как добавлять и удалять данных из
множества
Изучим ограничения, связанные с множествами
Узнаем об операциях: пересечение, объединение и вычитание
множеств
Посмотрим на реальные кейсы применения множеств
Поехали!
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
7.
ТеорияЧто такое множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
8.
ТеорияЧто такое множество
Что такое множество в математике?
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
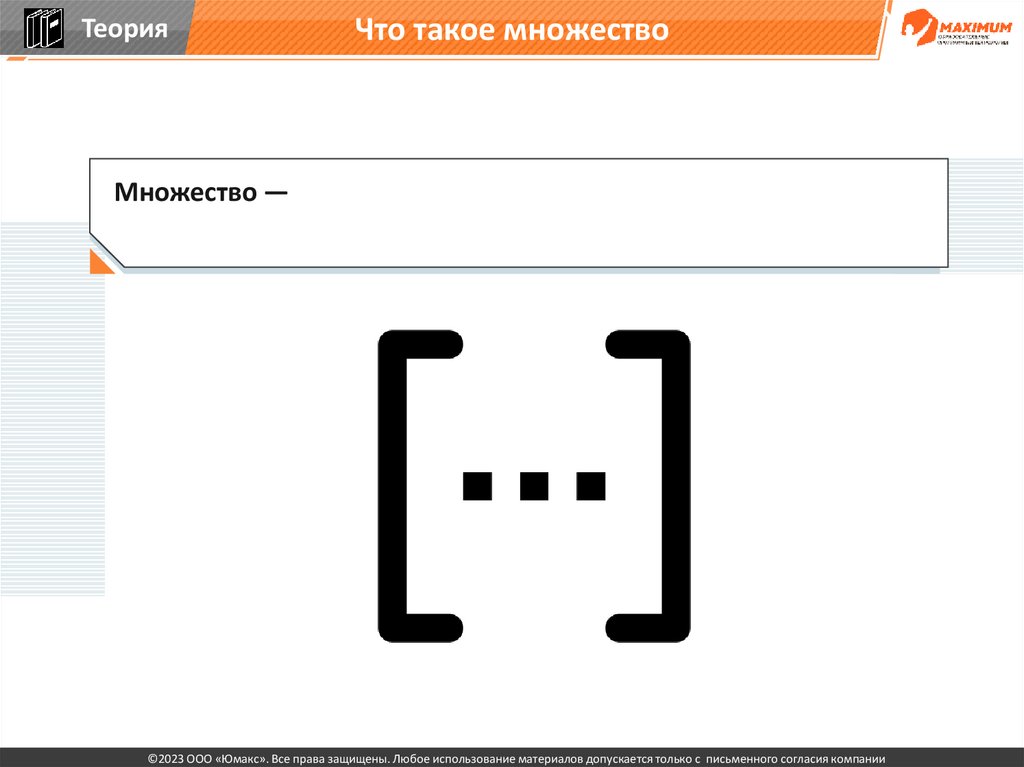
9.
ТеорияЧто такое множество
Множество —
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
10.
ТеорияЧто такое множество
Множество — одно из ключевых понятий математики,
представляющее собой набор, совокупность каких-либо объектов
— элементов этого множества.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
11.
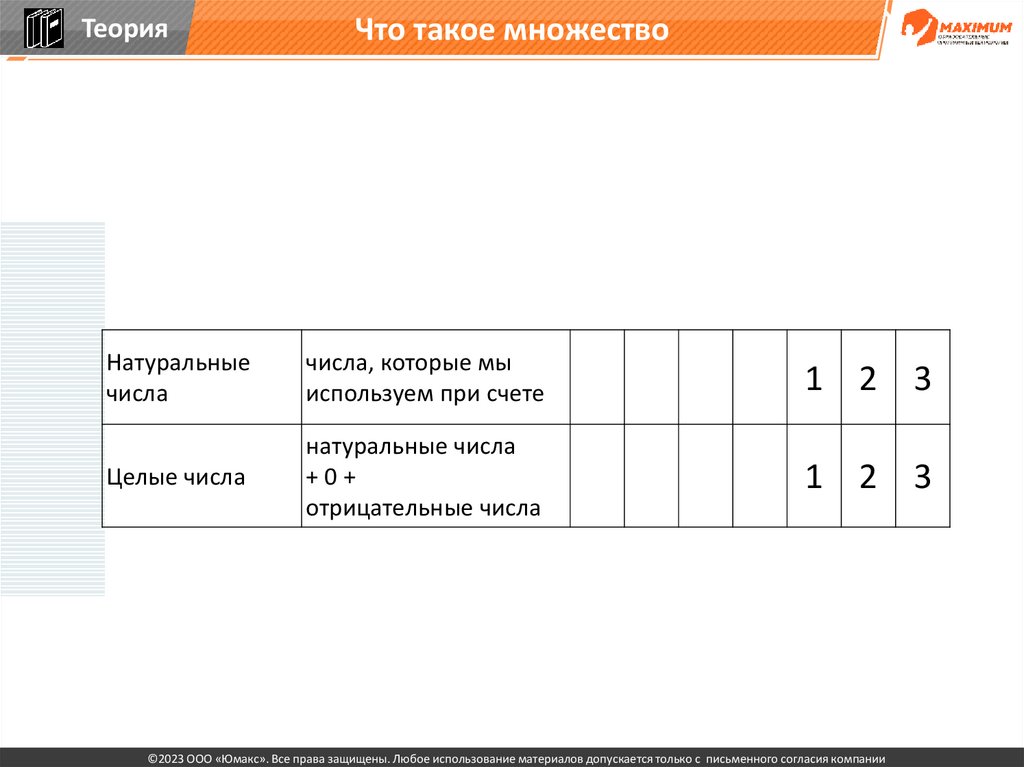
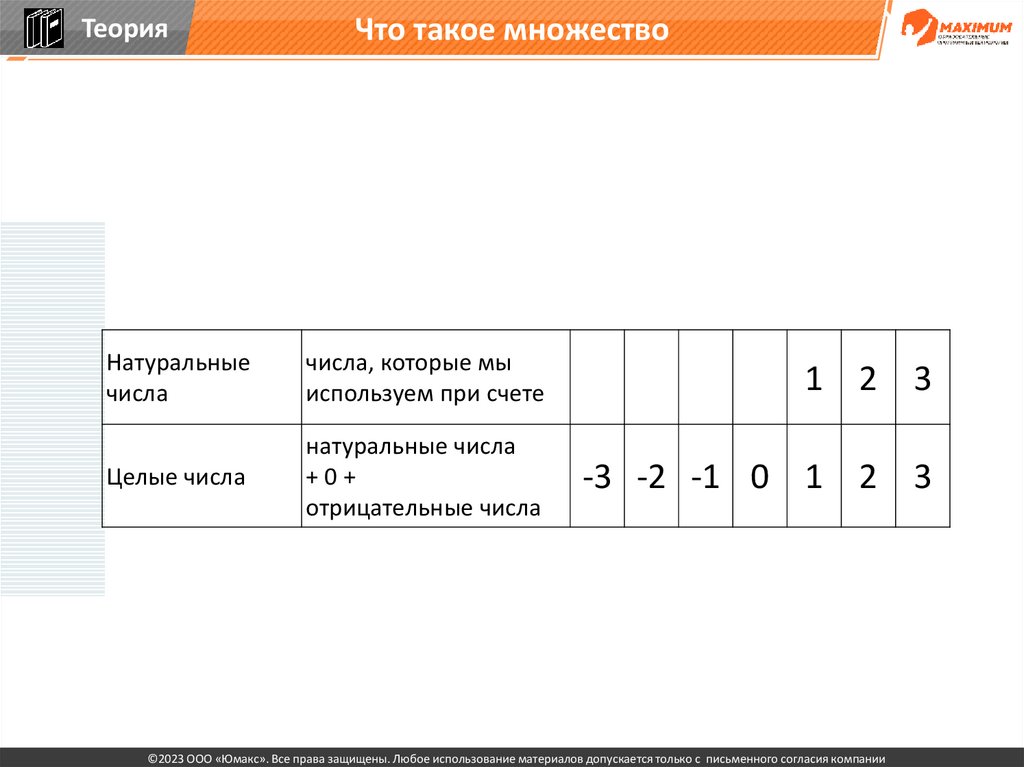
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
Целые числа
натуральные числа
+0+
отрицательные числа
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
12.
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
Целые числа
натуральные числа
+0+
отрицательные числа
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
13.
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
Целые числа
натуральные числа
+0+
отрицательные числа
1
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
14.
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
Целые числа
натуральные числа
+0+
отрицательные числа
1 2
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
15.
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
Целые числа
натуральные числа
+0+
отрицательные числа
1 2 3
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
16.
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
Целые числа
натуральные числа
+0+
отрицательные числа
1 2 3
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
17.
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
1 2 3
Целые числа
натуральные числа
+0+
отрицательные числа
1 2 3
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
18.
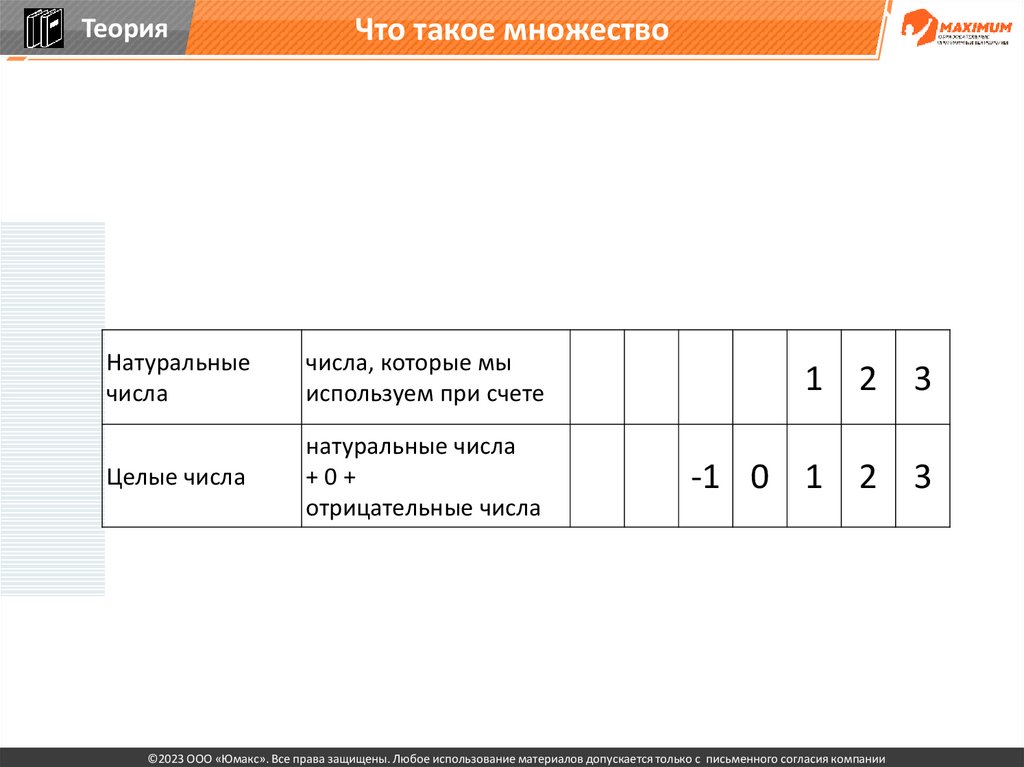
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
1 2 3
Целые числа
натуральные числа
+0+
отрицательные числа
-1 0 1 2 3
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
19.
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
1 2 3
Целые числа
натуральные числа
+0+
отрицательные числа
-2 -1 0 1 2 3
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
20.
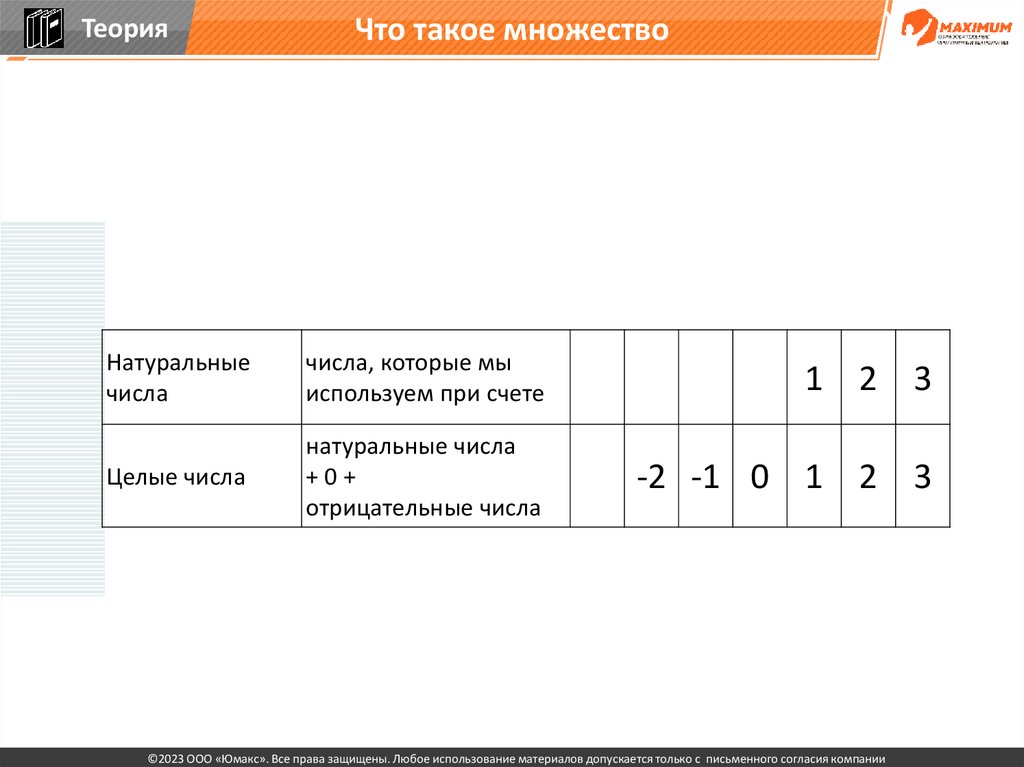
ТеорияЧто такое множество
Натуральные
числа
числа, которые мы
используем при счете
1 2 3
Целые числа
натуральные числа
+0+
отрицательные числа
-3 -2 -1 0 1 2 3
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
21.
Что такое множествоТеория
Натуральные
числа
числа, которые мы
используем при счете
1 2 3
Целые числа
натуральные числа
+0+
отрицательные числа
-3 -2 -1 0 1 2 3
Множество – это просто набор каких-то элементов!
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
22.
ТеорияЧто такое множество
Элементы в множестве представлены один раз,
то есть не повторяются
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
23.
ТеорияЧто такое множество
Какие операции можно производить с
множествами?
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
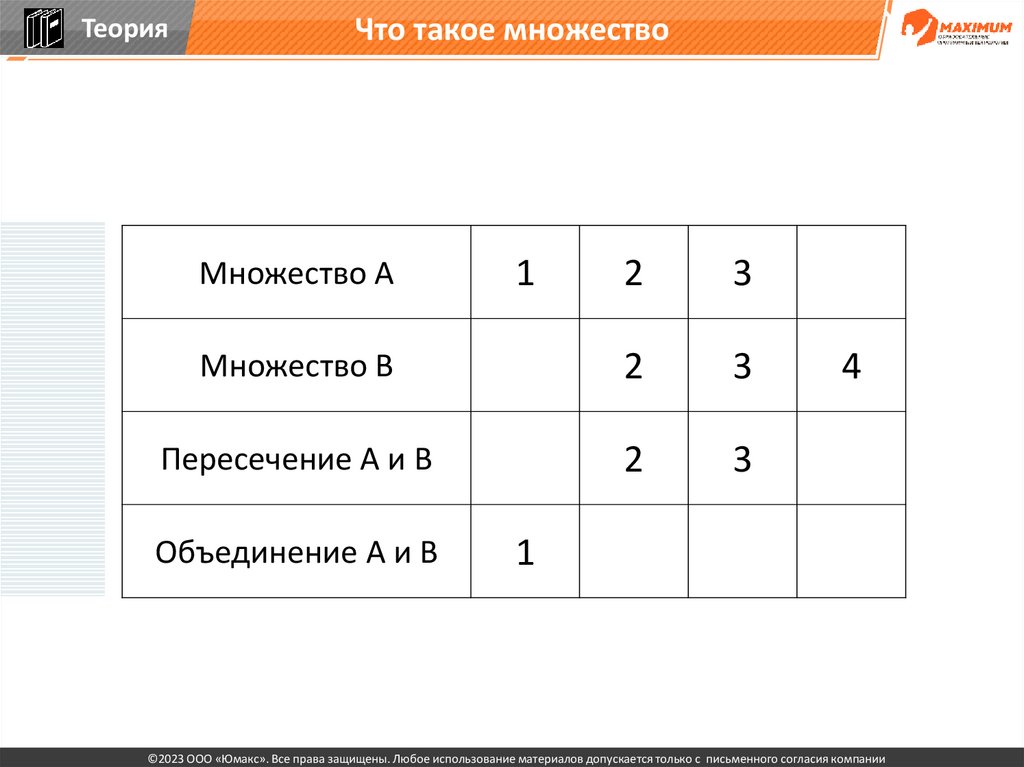
24.
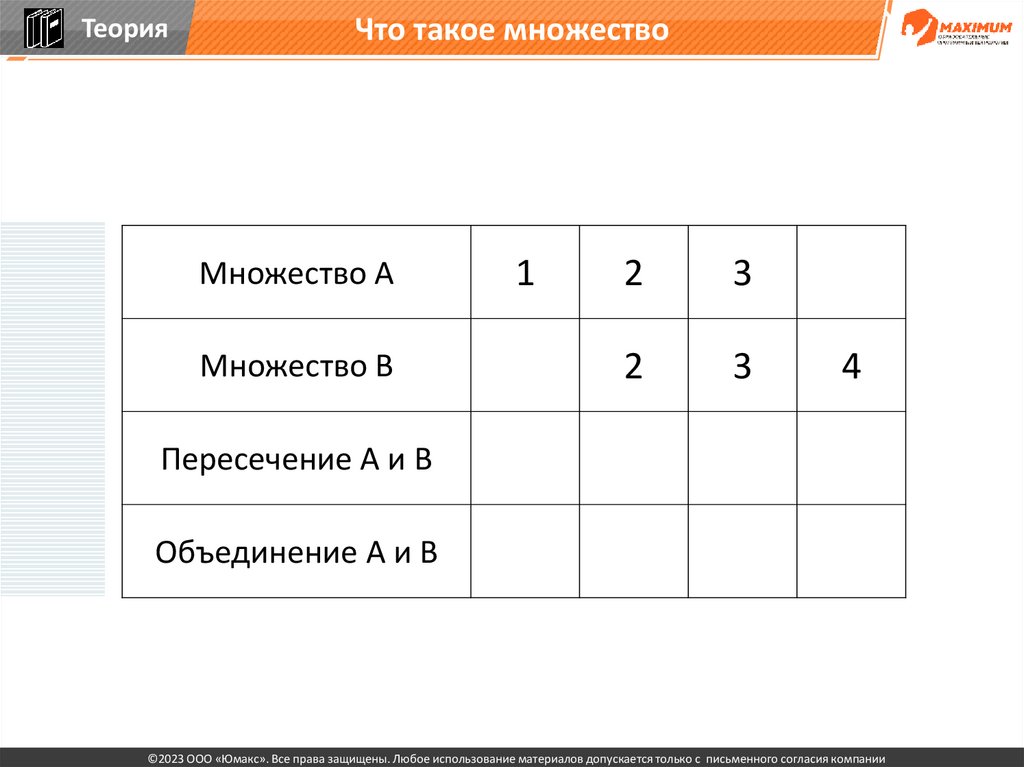
ТеорияЧто такое множество
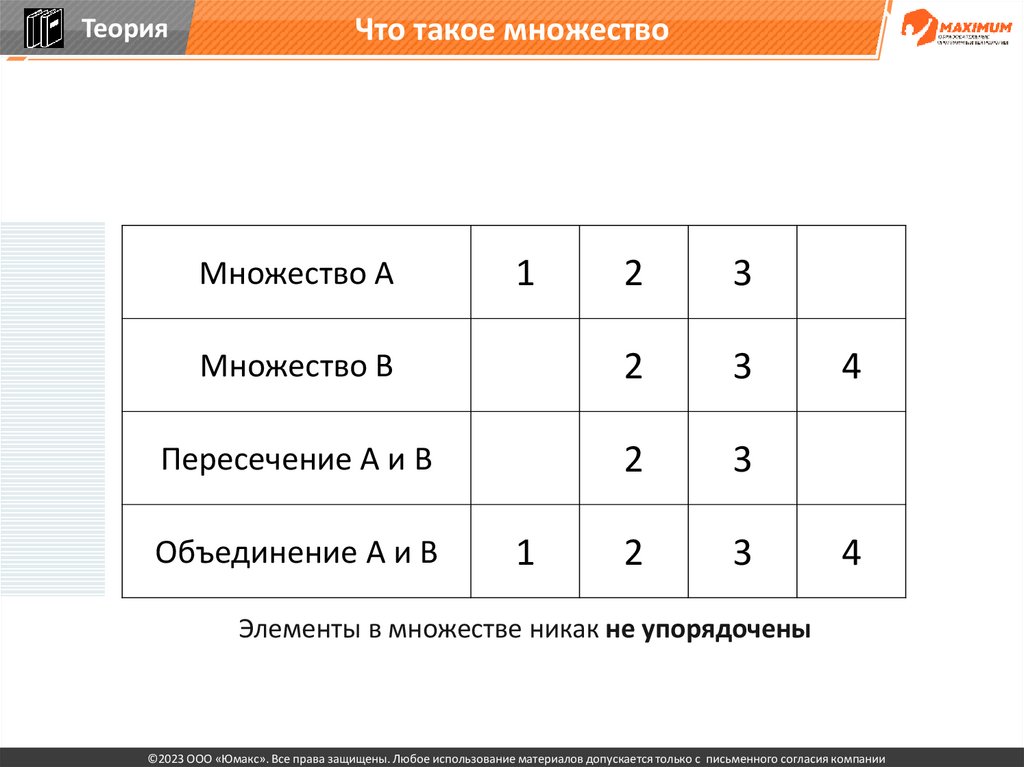
Множество А
Множество В
1
2
3
2
3
4
Пересечение А и В
Объединение А и В
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
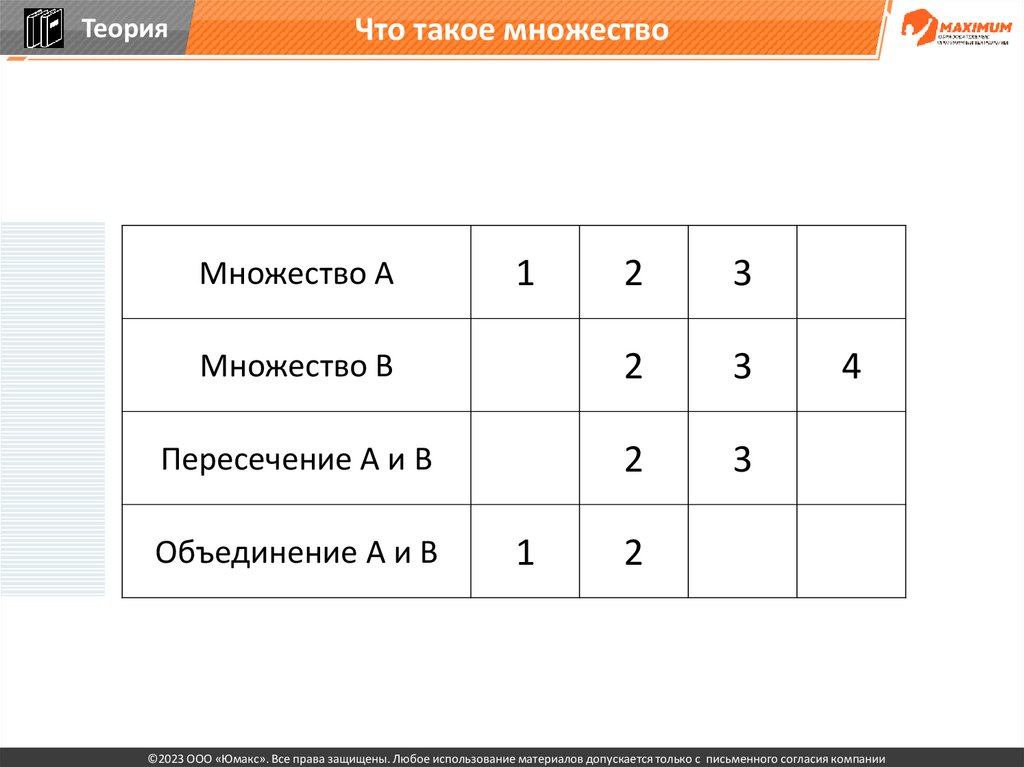
25.
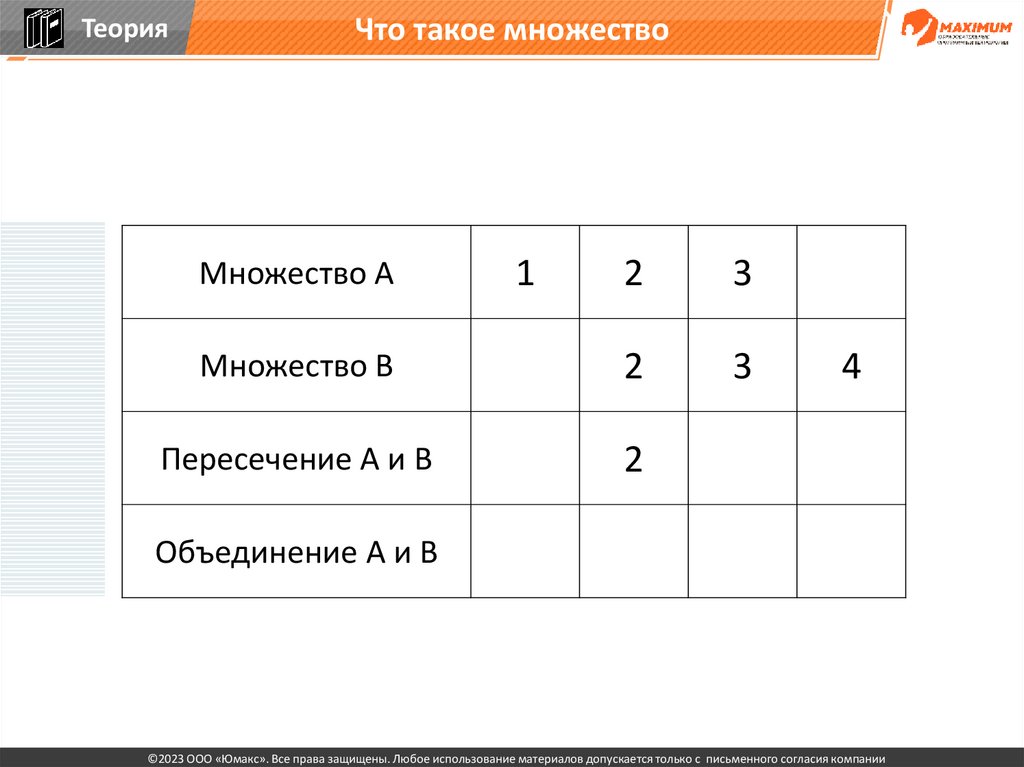
ТеорияЧто такое множество
2
3
Множество В
2
3
Пересечение А и В
2
Множество А
1
4
Объединение А и В
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
26.
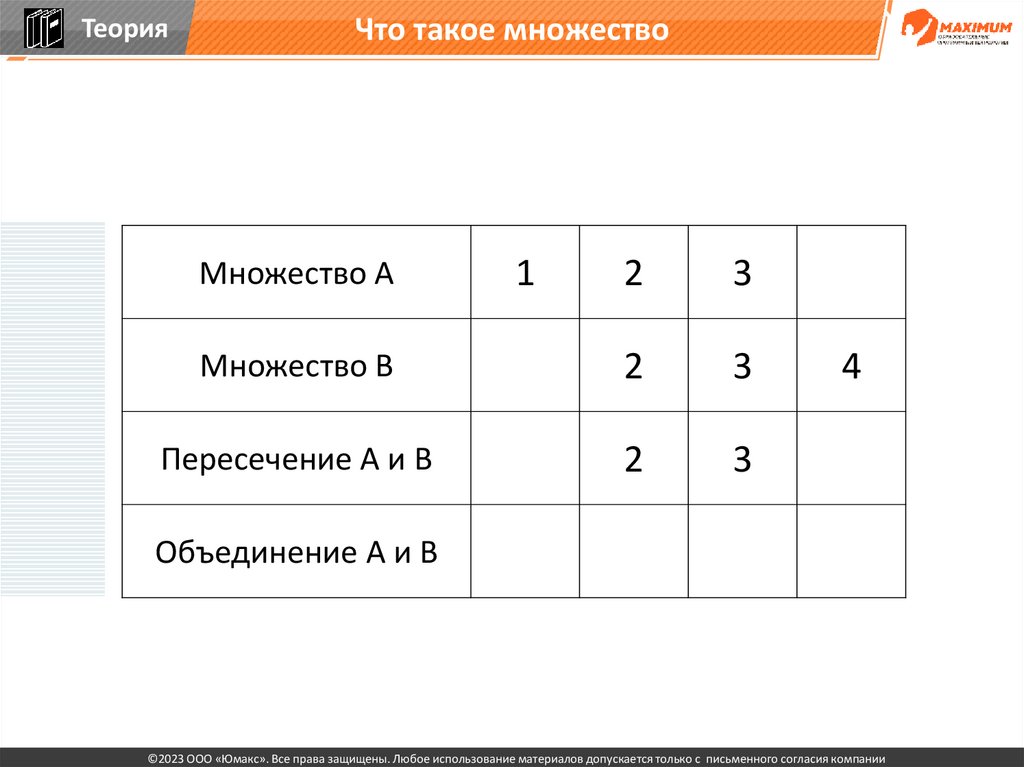
ТеорияЧто такое множество
2
3
Множество В
2
3
Пересечение А и В
2
3
Множество А
1
4
Объединение А и В
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
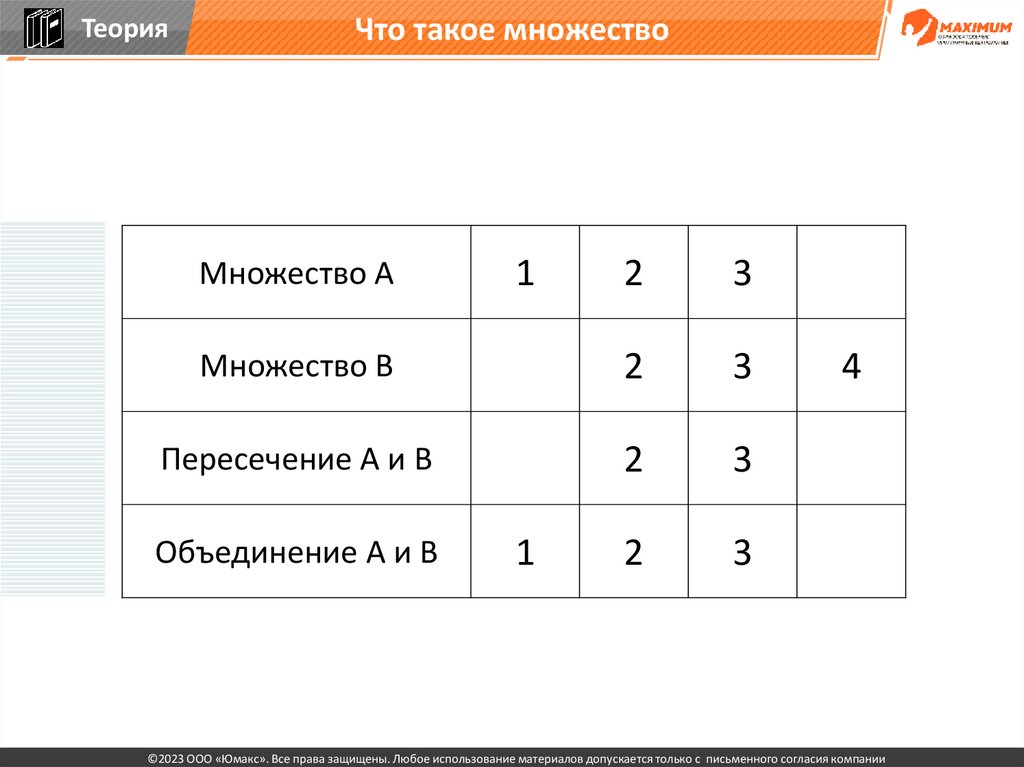
27.
ТеорияЧто такое множество
2
3
Множество В
2
3
Пересечение А и В
2
3
Множество А
Объединение А и В
1
4
1
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
28.
ТеорияЧто такое множество
2
3
Множество В
2
3
Пересечение А и В
2
3
Множество А
Объединение А и В
1
1
4
2
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
29.
ТеорияЧто такое множество
2
3
Множество В
2
3
Пересечение А и В
2
3
2
3
Множество А
Объединение А и В
1
1
4
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
30.
ТеорияЧто такое множество
2
3
Множество В
2
3
Пересечение А и В
2
3
2
3
Множество А
Объединение А и В
1
1
4
4
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
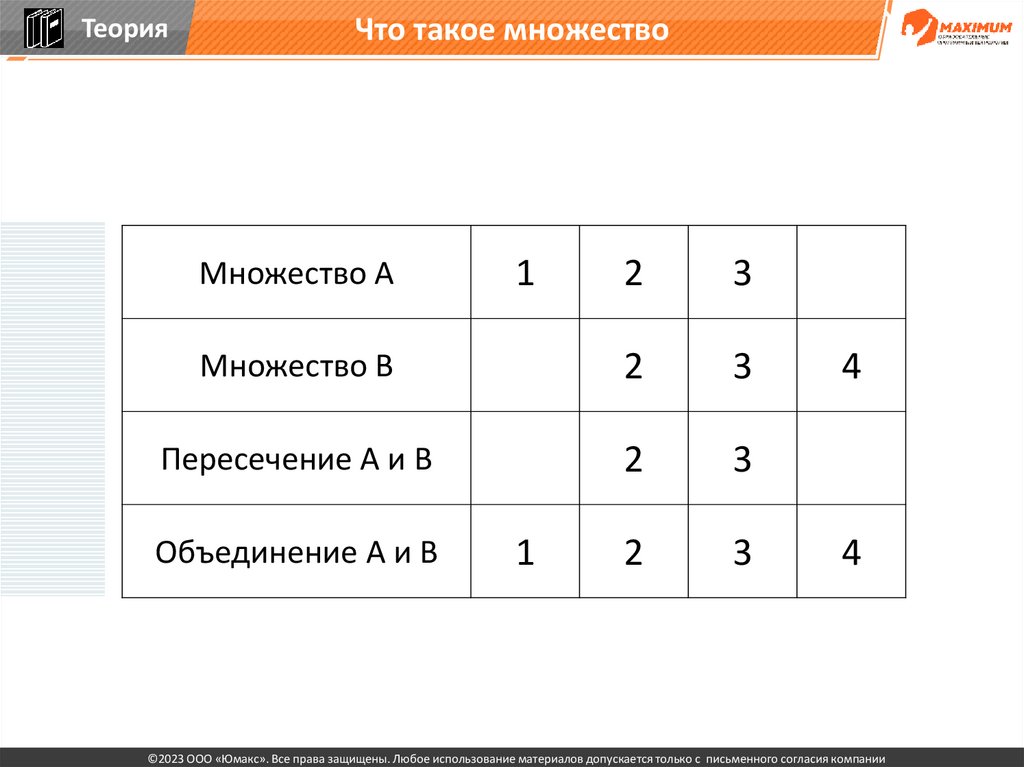
31.
ТеорияЧто такое множество
2
3
Множество В
2
3
Пересечение А и В
2
3
2
3
Множество А
Объединение А и В
1
1
4
4
Элементы в множестве никак не упорядочены
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
32.
ТеорияСтруктура данных set
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
33.
ТеорияСтруктура данных set
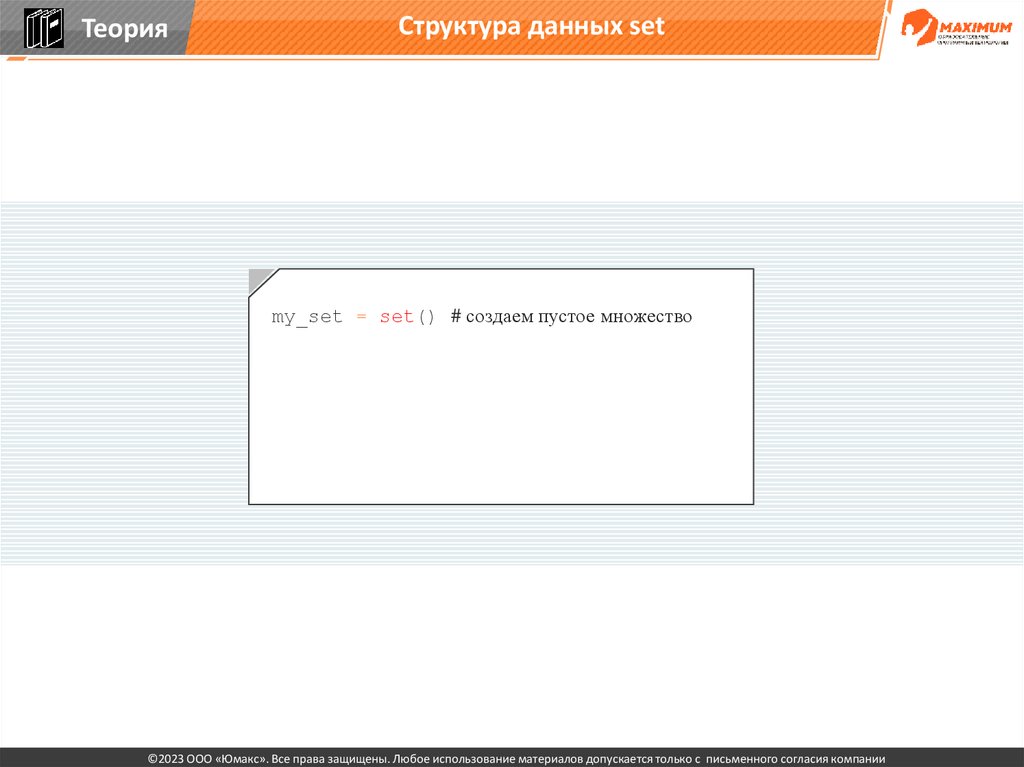
my_set = set() # создаем пустое множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
34.
ТеорияСтруктура данных set
my_set = set() # создаем пустое множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
35.
ТеорияСтруктура данных set
my_set = set() # создаем пустое множество
set()
«набор|множество»
Функция создает
пустое множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
36.
ТеорияСтруктура данных set
my_set = set() # создаем пустое множество
my_set_2 = {1, 2, 3} # заполненное множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
37.
ТеорияСтруктура данных set
my_set = set() # создаем пустое множество
my_set_2 = {1, 2, 3} # заполненное множество
Обязательно
перечисляем
элементы множества.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
38.
ТеорияСтруктура данных set
my_set = set() # создаем пустое множество
my_set_2 = {1, 2, 3} # заполненное множество
Обязательно
перечисляем
элементы множества.
Если оставим пустые
фигурные скобки –
получим словарь
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
39.
ТеорияСтруктура данных set
my_set = set() # создаем пустое множество
my_set_2 = {1, 2, 3} # заполненное множество
как мы можем
проверить тип
данных?
Обязательно
перечисляем
элементы множества.
Если оставим пустые
фигурные скобки –
получим словарь
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
40.
Теорияиспользовать
функцию type()
как мы можем
проверить тип
данных?
Структура данных set
my_set = set() # создаем пустое множество
my_set_2 = {1, 2, 3} # заполненное множество
Обязательно
перечисляем
элементы множества.
Если оставим пустые
фигурные скобки –
получим словарь
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
41.
Теорияиспользовать
функцию type()
как мы можем
проверить тип
данных?
Структура данных set
my_set = set() # создаем пустое множество
my_set_2 = {1, 2, 3} # заполненное множество
print(type(my_set_2))
Обязательно
перечисляем
элементы множества.
Если оставим пустые
фигурные скобки –
получим словарь
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
42.
Теорияиспользовать
функцию type()
Структура данных set
my_set = set() # создаем пустое множество
my_set_2 = {1, 2, 3} # заполненное множество
print(type(my_set_2))
>>> <class 'set'>
как мы можем
проверить тип
данных?
Обязательно
перечисляем
элементы множества.
Если оставим пустые
фигурные скобки –
получим словарь
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
43.
ТеорияДобавление и удаление данных
из множества
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
44.
Добавление и удалениеТеория
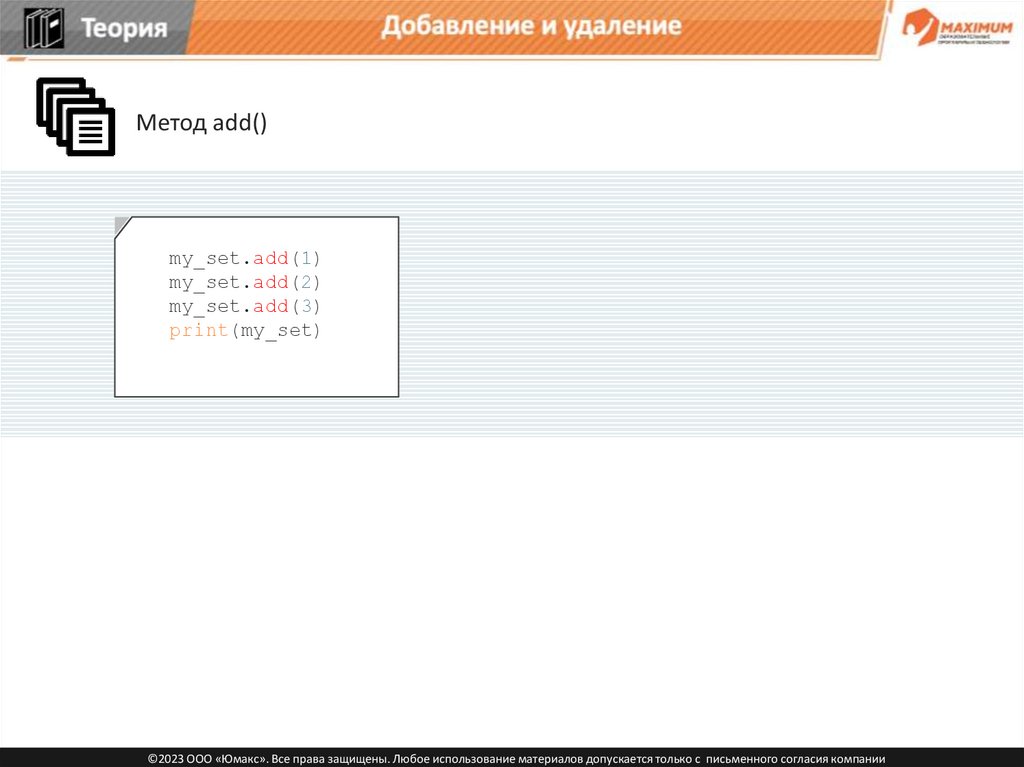
Метод add()
my_set.add(1)
my_set.add(2)
my_set.add(3)
print(my_set)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
45.
Добавление и удалениеТеория
Метод add()
my_set.add(1)
my_set.add(2)
my_set.add(3)
print(my_set)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
46.
Добавление и удалениеТеория
Метод add()
my_set.add(1)
my_set.add(2)
my_set.add(3)
print(my_set)
{1, 2, 3}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
47.
Добавление и удалениеТеория
Метод add()
my_set.add(1)
my_set.add(2)
my_set.add(3)
print(my_set)
{1, 2, 3}
как переводится слово
add?
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
48.
Добавление и удалениеТеория
Метод add()
my_set.add(1)
my_set.add(2)
my_set.add(3)
print(my_set)
{1, 2, 3}
как переводится слово
add?
Добавить!
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
49.
Добавление и удалениеТеория
Метод add()
my_set.add(1)
my_set.add(2)
my_set.add(3)
print(my_set)
add()
{1, 2, 3}
метод, позволяющий
добавить в множество
новый элемент
как переводится слово
add?
Добавить!
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
50.
ТеорияДобавление и удаление
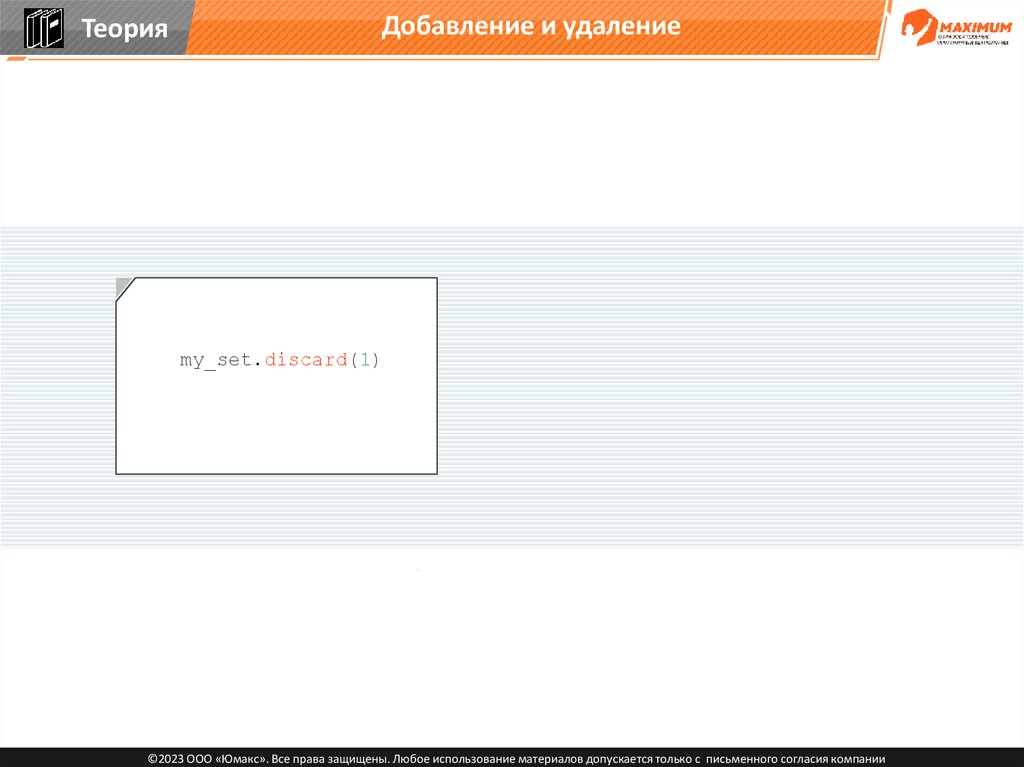
my_set.discard(1)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
51.
ТеорияДобавление и удаление
my_set.discard(1)
discard()
метод, позволяющий удалить из
множества указанный элемент
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
52.
ТеорияДобавление и удаление
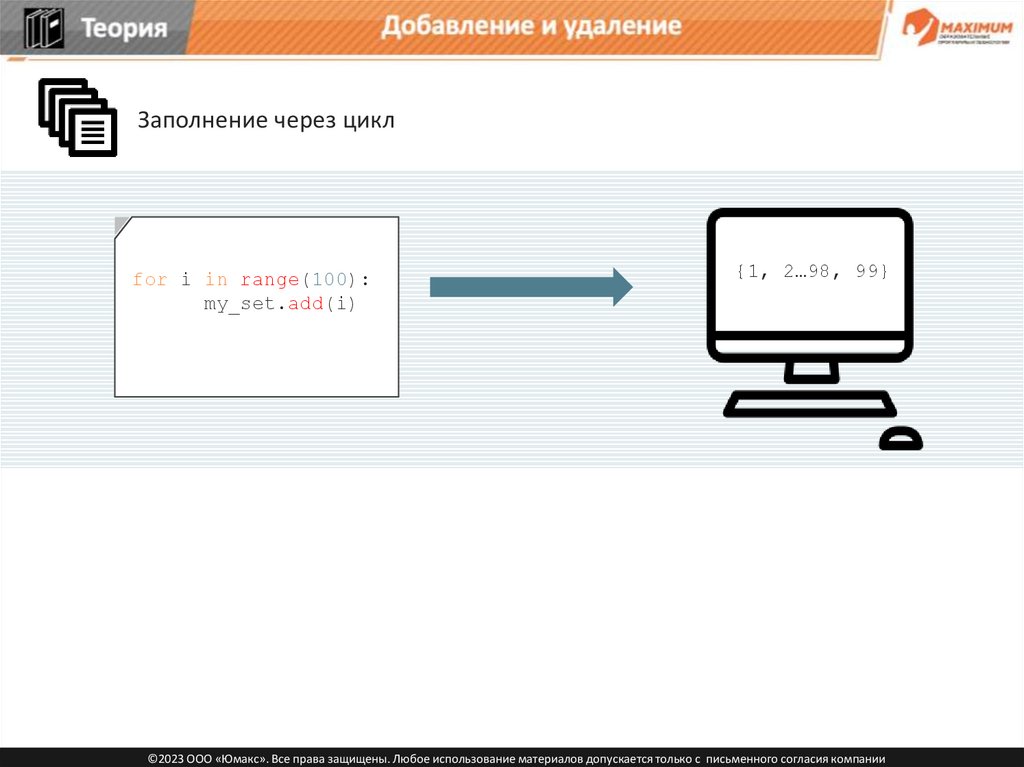
Заполнение через цикл
for i in range(100):
my_set.add(i)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
53.
ТеорияДобавление и удаление
Заполнение через цикл
for i in range(100):
my_set.add(i)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
54.
ТеорияДобавление и удаление
Заполнение через цикл
for i in range(100):
my_set.add(i)
{1, 2…98, ?}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
55.
ТеорияДобавление и удаление
Заполнение через цикл
for i in range(100):
my_set.add(i)
{1, 2…98, 99}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
56.
Добавление и удалениеТеория
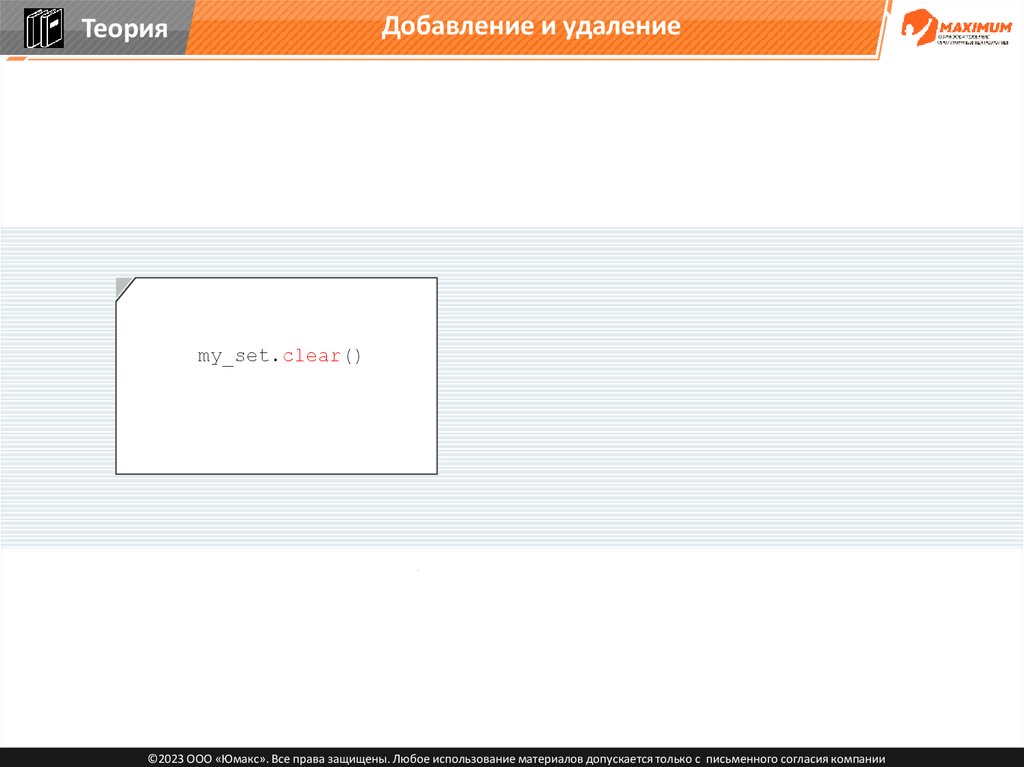
my_set.clear()
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
57.
Добавление и удалениеТеория
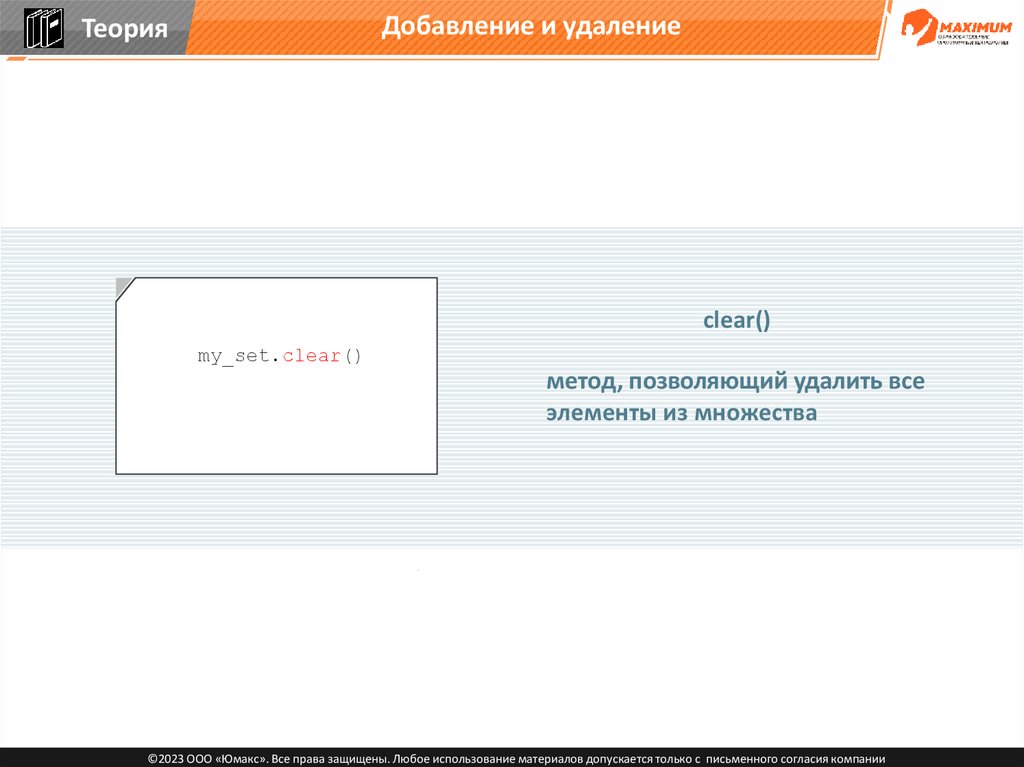
clear()
my_set.clear()
метод, позволяющий удалить все
элементы из множества
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
58.
ТеорияОграничения, связанные
с множествами
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
59.
ТеорияОграничения
Что мы не можем делать с множествами
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
60.
ТеорияОграничения
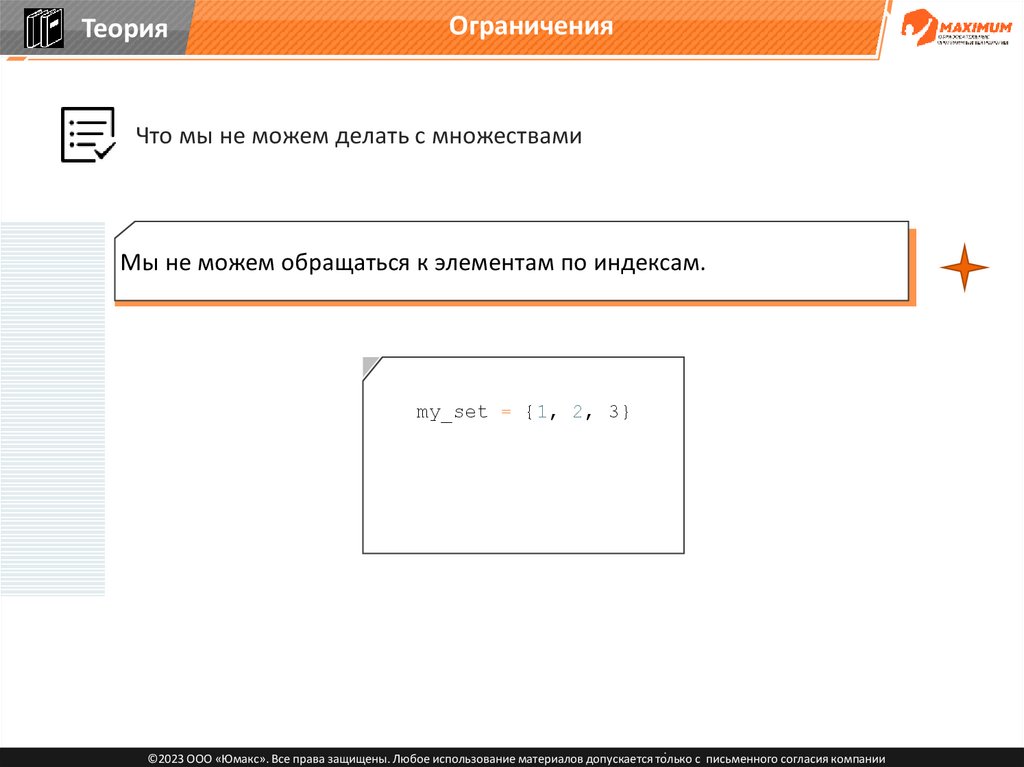
Что мы не можем делать с множествами
Мы не можем обращаться к элементам по индексам.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
61.
ТеорияОграничения
Что мы не можем делать с множествами
Мы не можем обращаться к элементам по индексам.
my_set = {1, 2, 3}
print(my_set[0])
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
62.
ТеорияОграничения
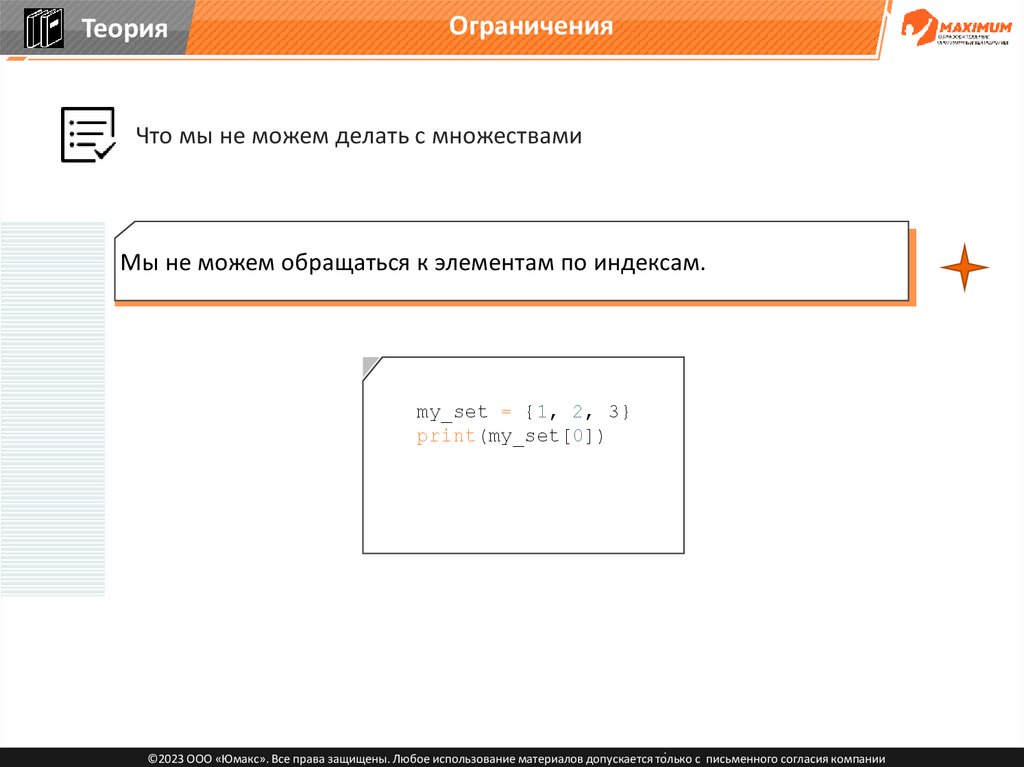
Что мы не можем делать с множествами
Мы не можем обращаться к элементам по индексам.
my_set = {1, 2, 3}
print(my_set[0])
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
63.
ТеорияОграничения
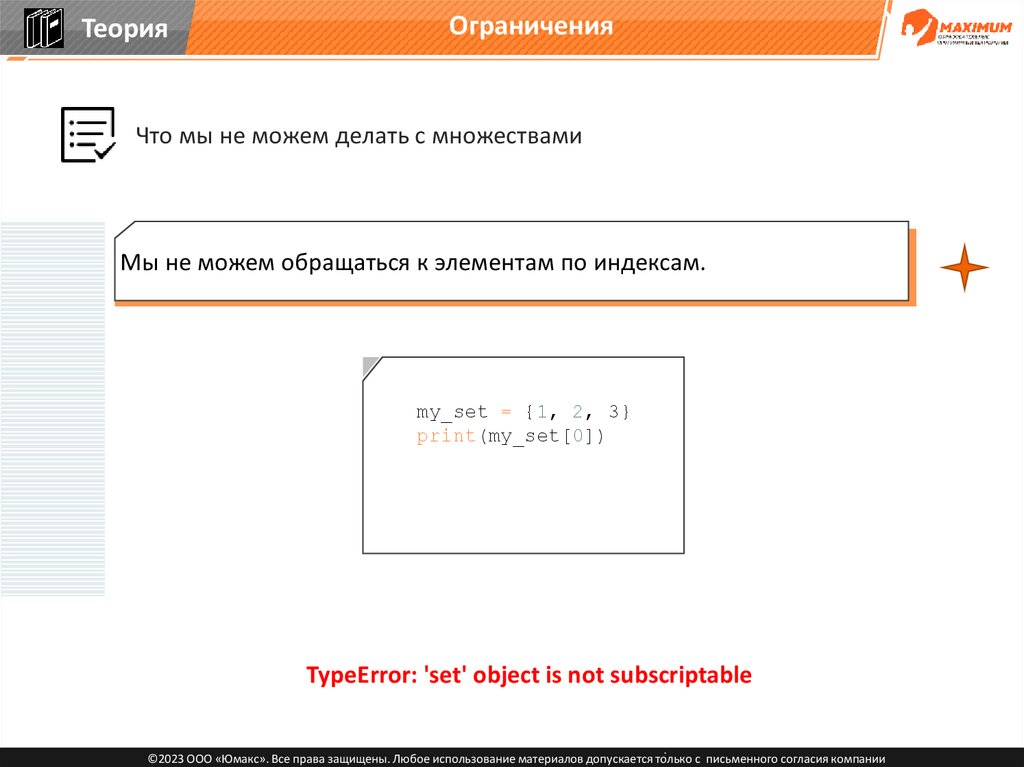
Что мы не можем делать с множествами
Мы не можем обращаться к элементам по индексам.
my_set = {1, 2, 3}
print(my_set[0])
TypeError: 'set' object is not subscriptable
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
64.
ТеорияОграничения
Что мы не можем делать с множествами
Мы не можем обращаться к элементам по индексам.
В множестве могут храниться только неизменяемые типы данных
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
65.
ТеорияОграничения
Что мы не можем делать с множествами
Мы не можем обращаться к элементам по индексам.
В множестве могут храниться только неизменяемые типы данных
my_set = {1, 2, 3}
my_set.add([4, 5])
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
66.
ТеорияОграничения
Что мы не можем делать с множествами
Мы не можем обращаться к элементам по индексам.
В множестве могут храниться только неизменяемые типы данных
my_set = {1, 2, 3}
my_set.add([4, 5])
TypeError: unhashable type: 'list'
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
67.
ТеорияОграничения
Что мы не можем делать с множествами
Мы не можем обращаться к элементам по индексам.
В множестве могут храниться только неизменяемые типы данных
В множестве не могут храниться списки
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
68.
ТеорияПересечение, объединение и
вычитание множеств
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
69.
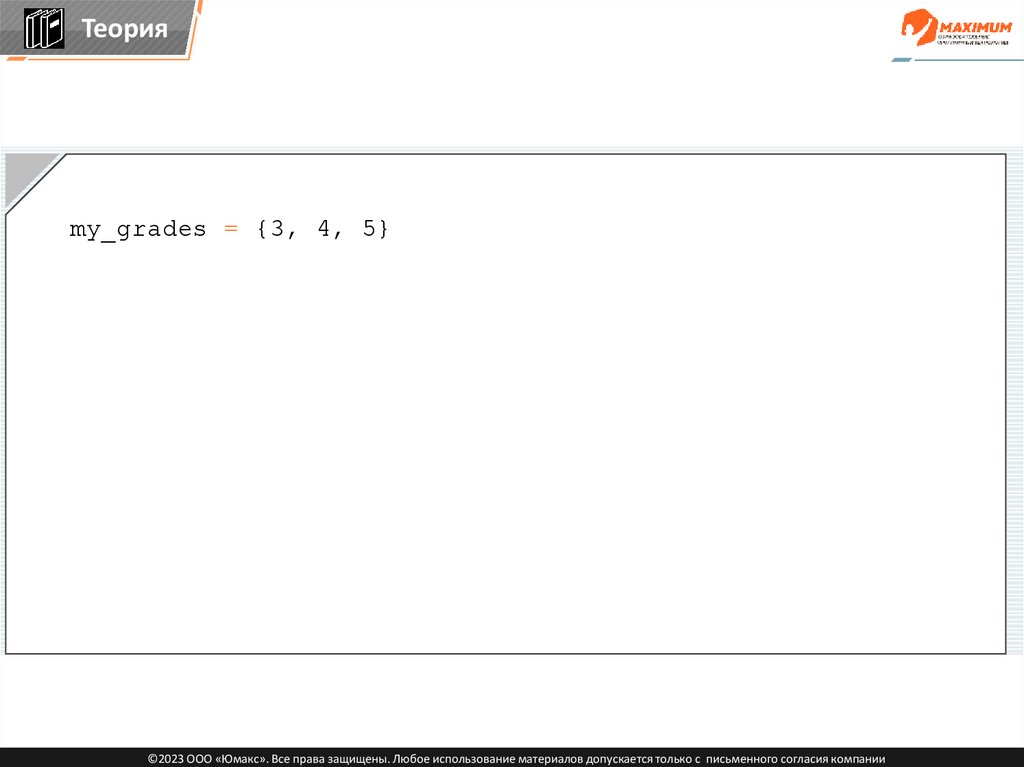
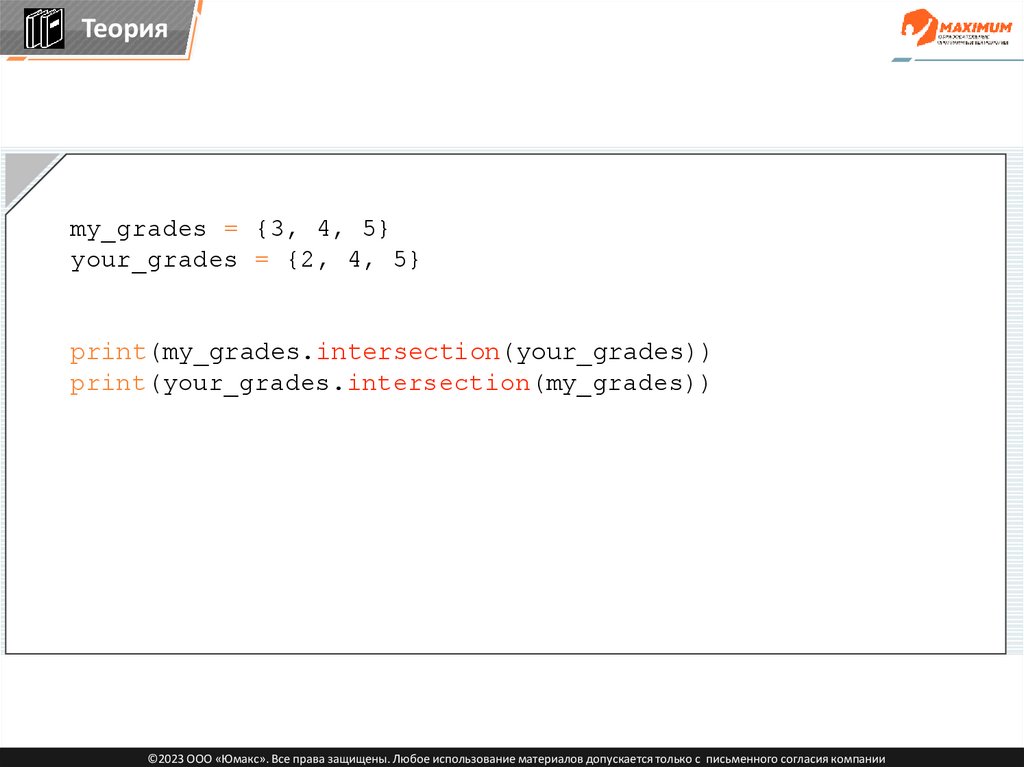
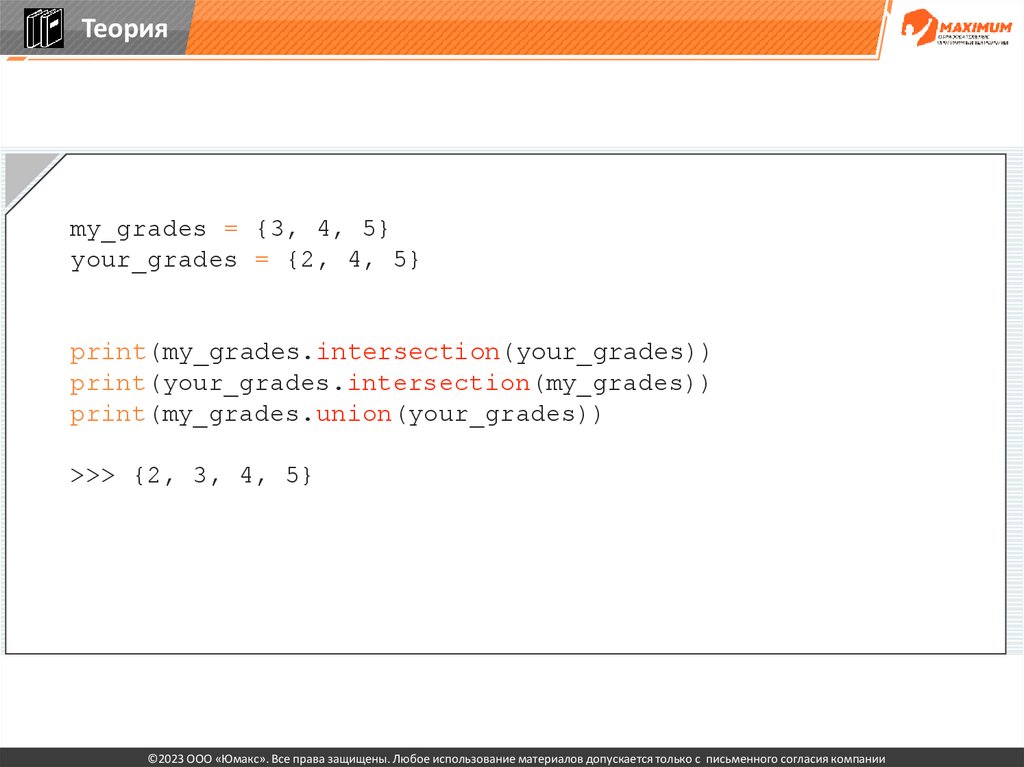
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
70.
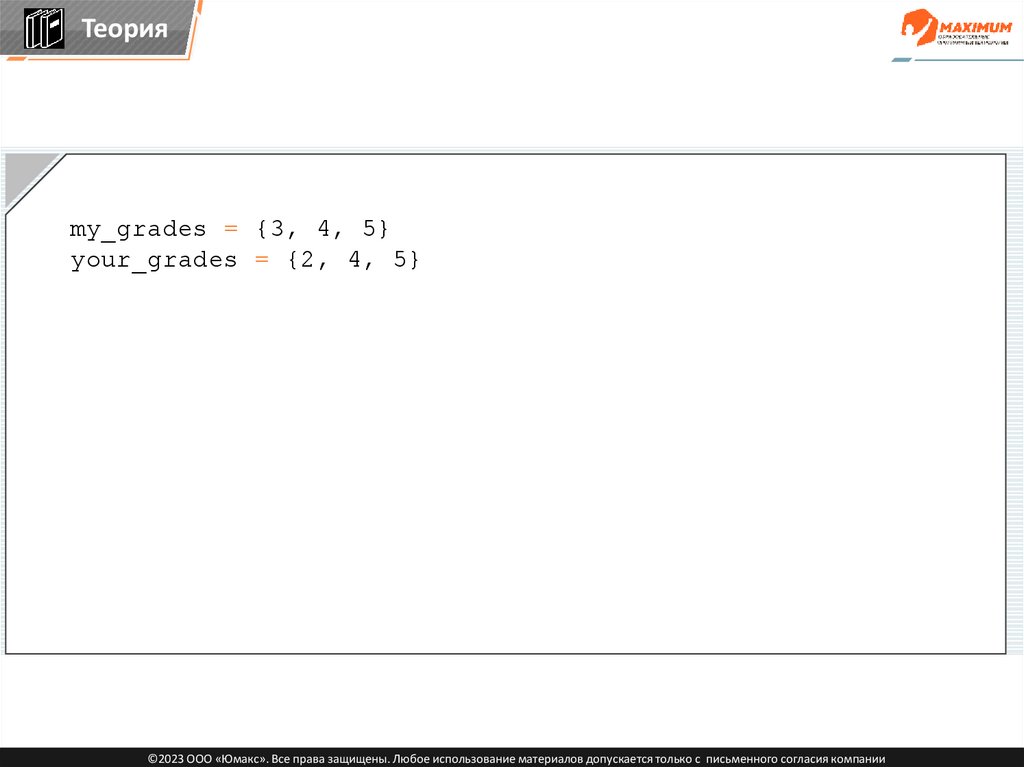
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
71.
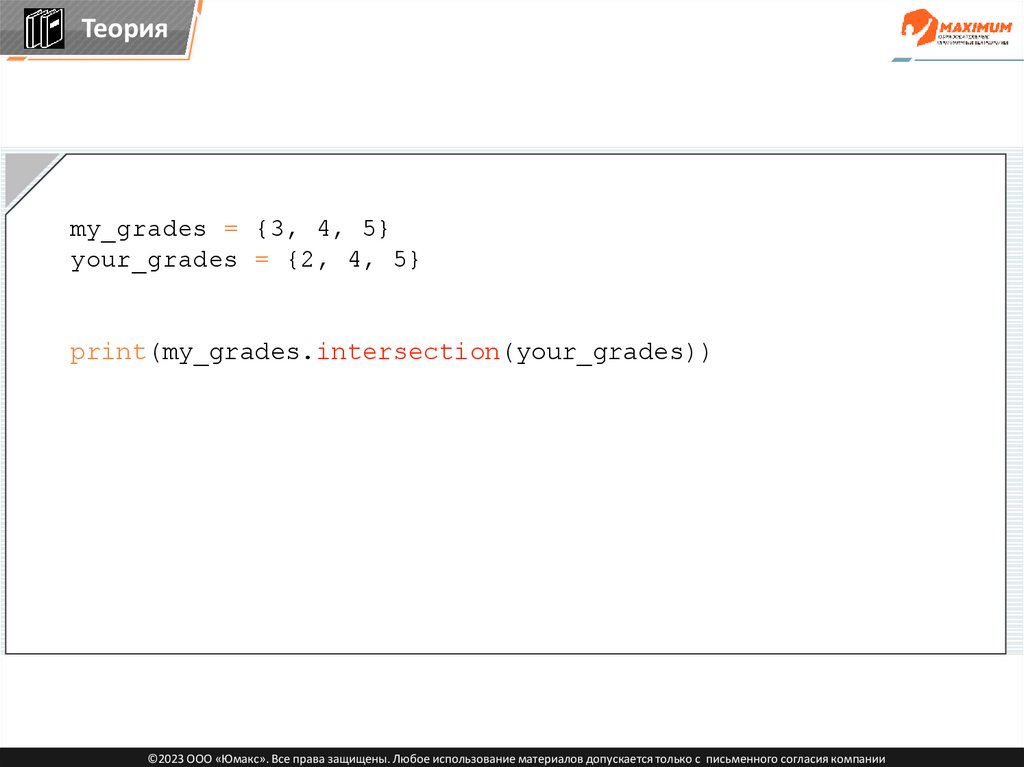
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
72.
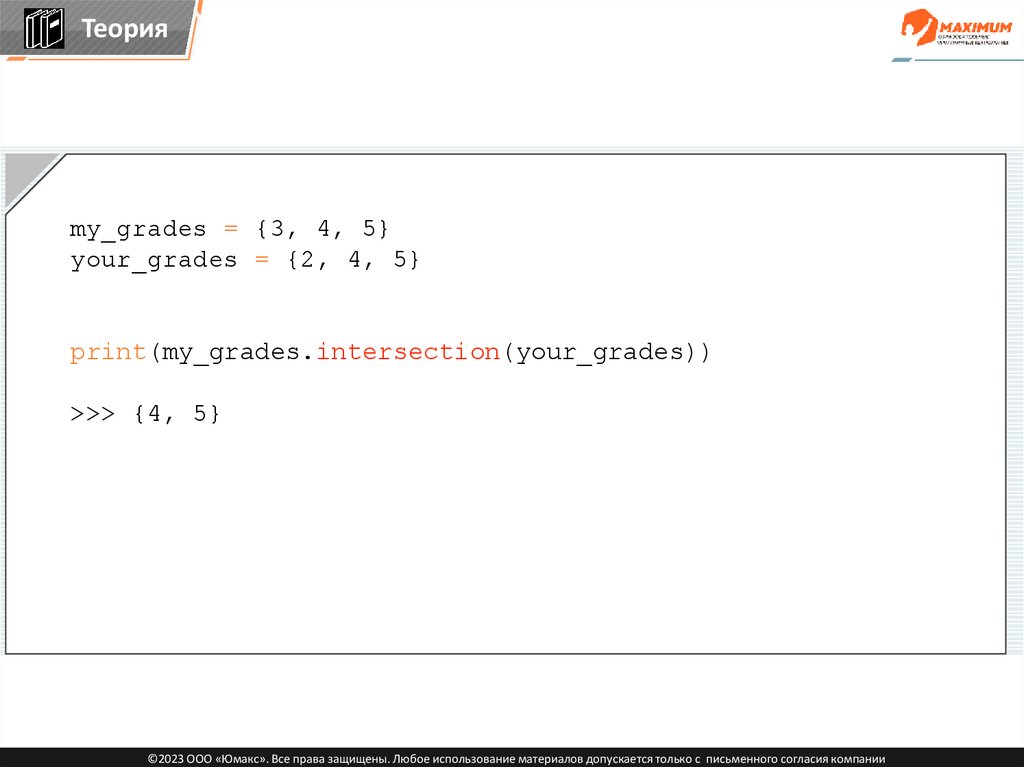
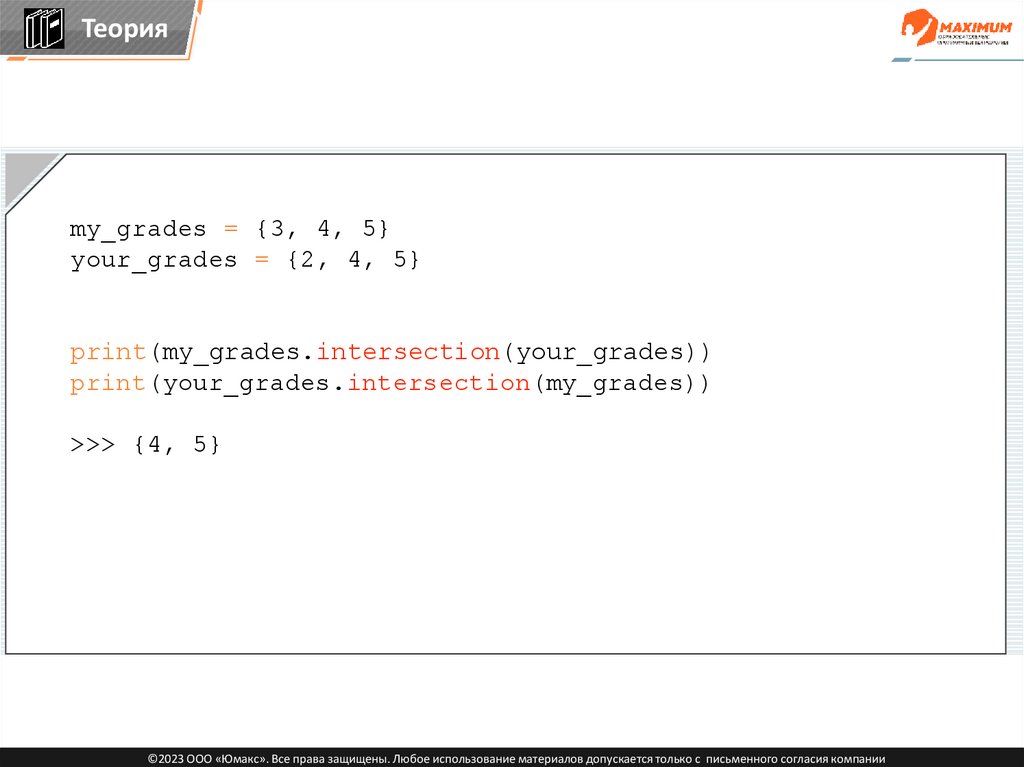
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
>>> {4, 5}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
73.
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
74.
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
>>> {4, 5}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
75.
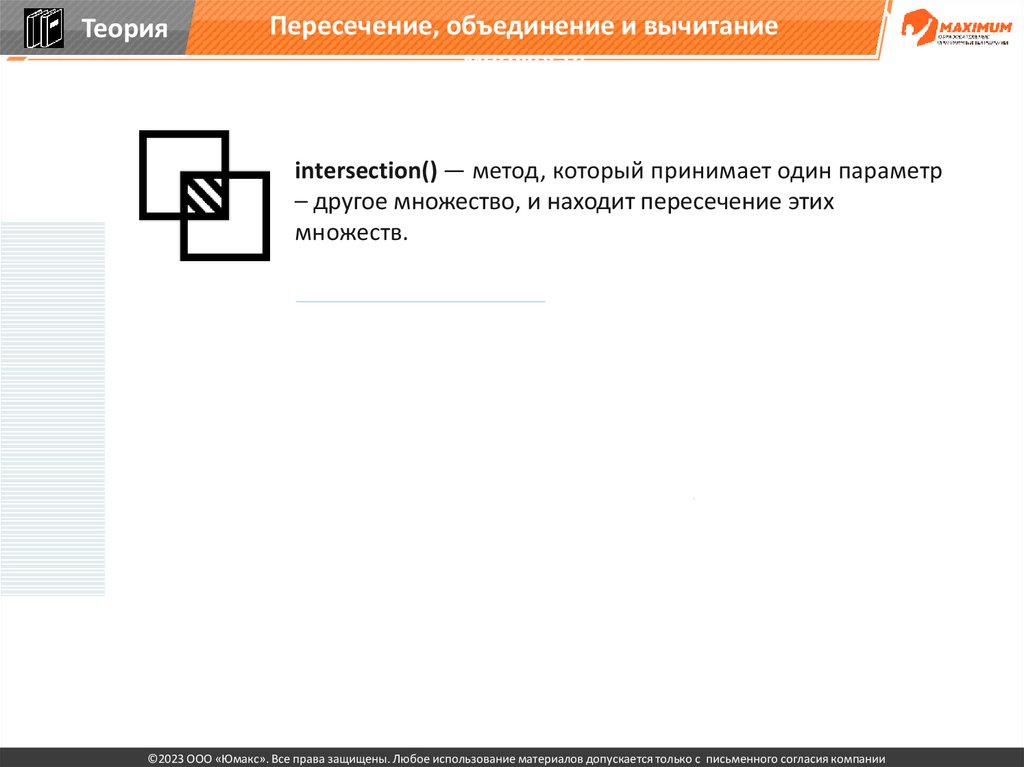
ТеорияПересечение, объединение и вычитание
множеств
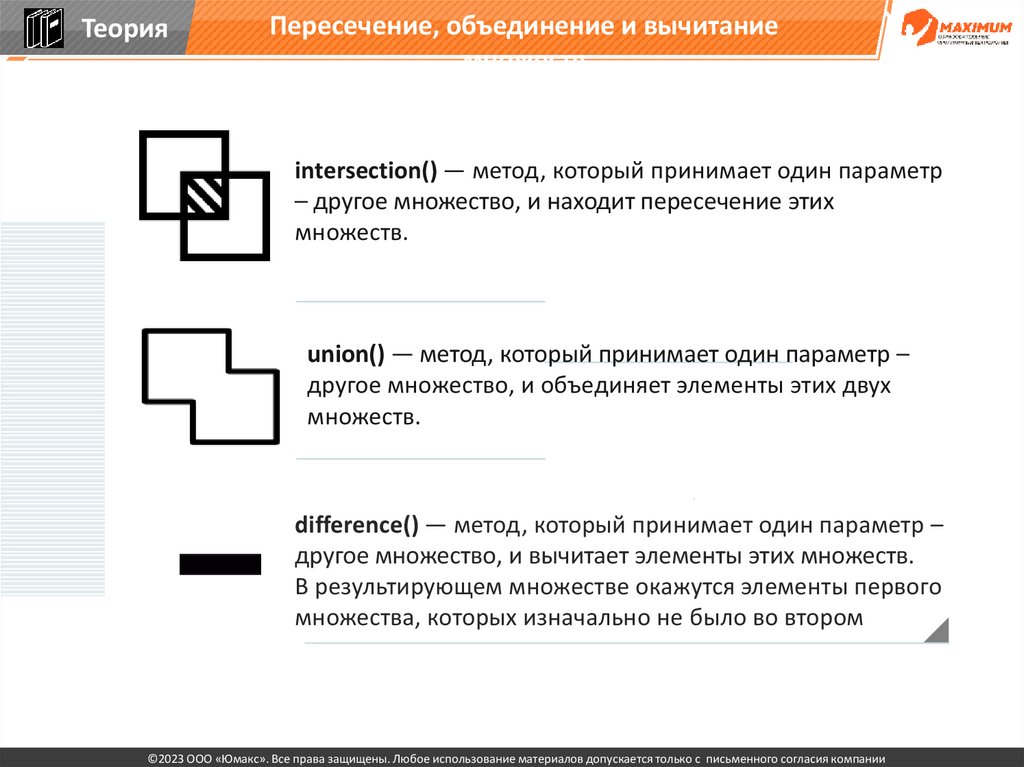
intersection() — метод, который принимает один параметр
– другое множество, и находит пересечение этих
множеств.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
76.
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
print(my_grades.union(your_grades))
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
77.
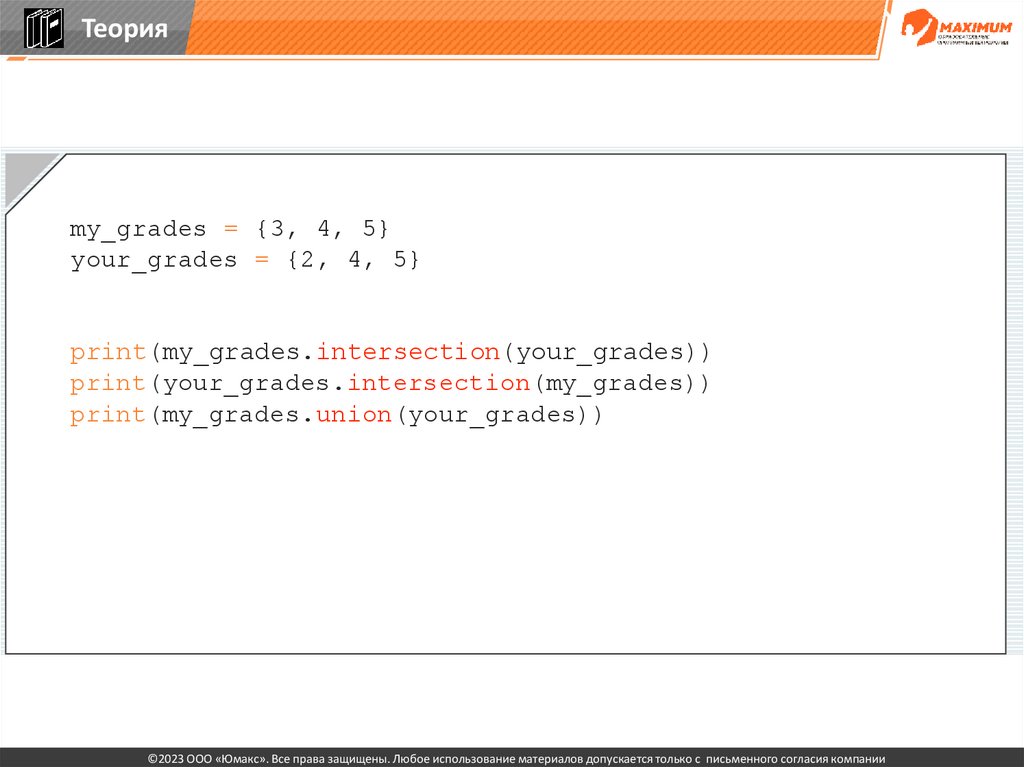
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
print(my_grades.union(your_grades))
>>> {2, 3, 4, 5}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
78.
ТеорияПересечение, объединение и вычитание
множеств
intersection() — метод, который принимает один параметр
– другое множество, и находит пересечение этих
множеств.
union() — метод, который принимает один параметр –
другое множество, и объединяет элементы этих двух
множеств.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
79.
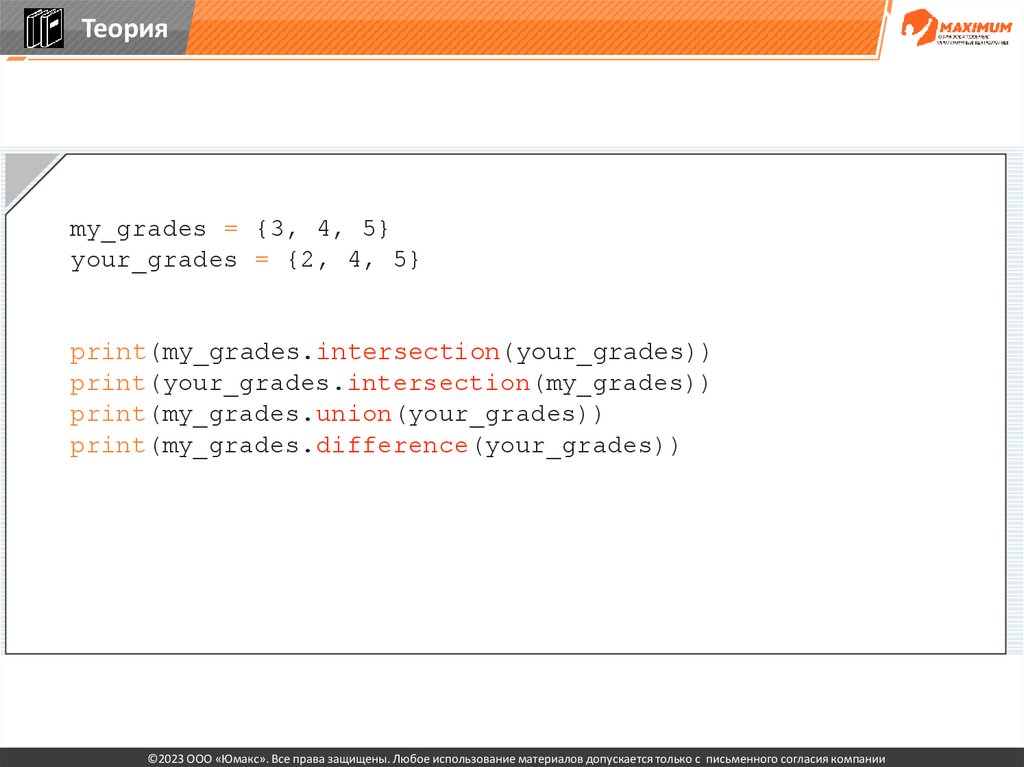
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
print(my_grades.union(your_grades))
print(my_grades.difference(your_grades))
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
80.
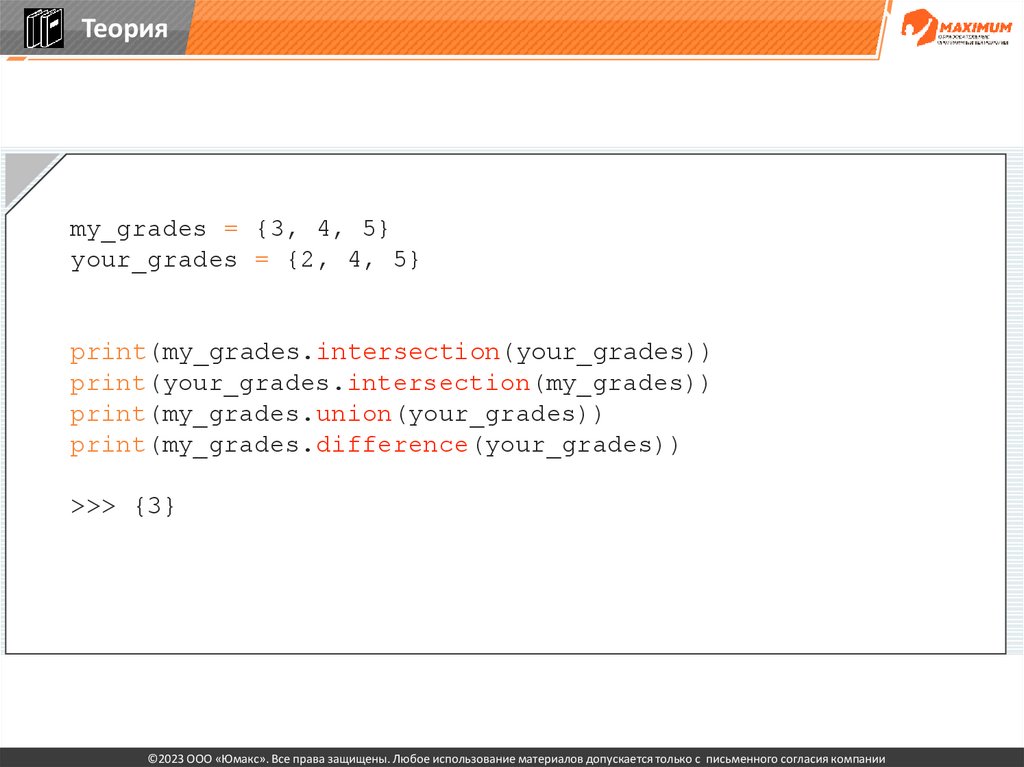
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
print(my_grades.intersection(your_grades))
print(your_grades.intersection(my_grades))
print(my_grades.union(your_grades))
print(my_grades.difference(your_grades))
>>> {3}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
81.
ТеорияПересечение, объединение и вычитание
множеств
intersection() — метод, который принимает один параметр
– другое множество, и находит пересечение этих
множеств.
union() — метод, который принимает один параметр –
другое множество, и объединяет элементы этих двух
множеств.
difference() — метод, который принимает один параметр –
другое множество, и вычитает элементы этих множеств.
В результирующем множестве окажутся элементы первого
множества, которых изначально не было во втором
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
82.
ТеорияПересечение, объединение и вычитание
множеств
Эти операции не обновляют текущее множество, а создают новое.
Если нам нужно именно обновить текущее множество, то для этого
следует использовать те же методы, но с дополнением в конце
«_update»
update() – метод, работающий как union(), только обновляет
исходное множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
83.
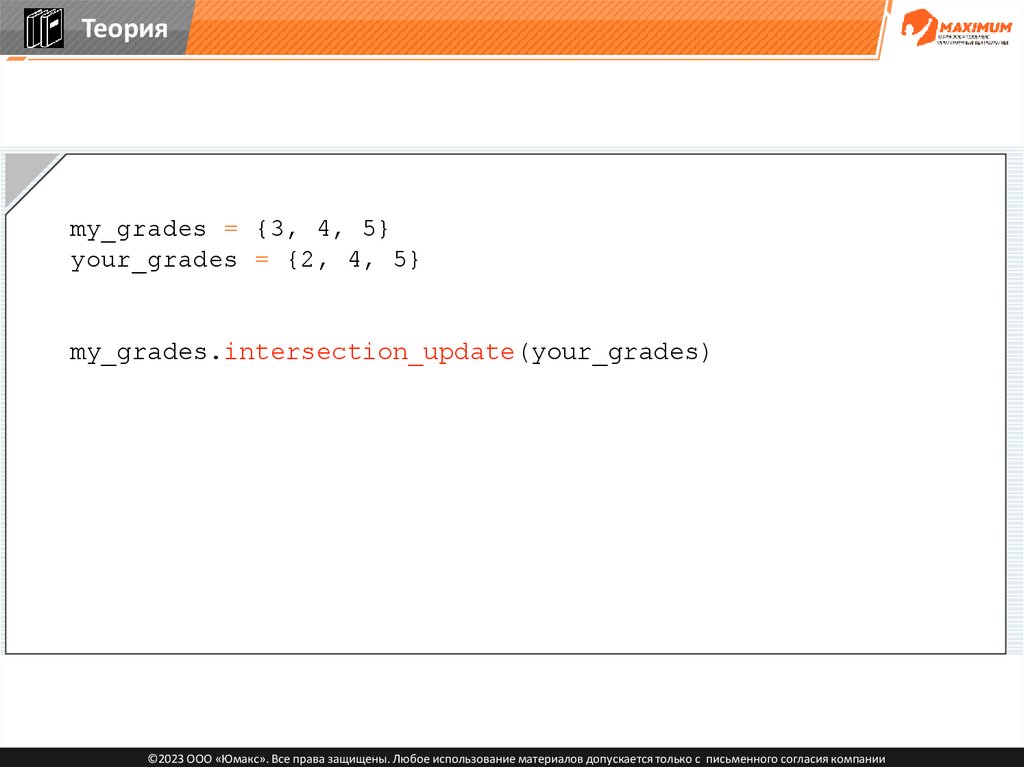
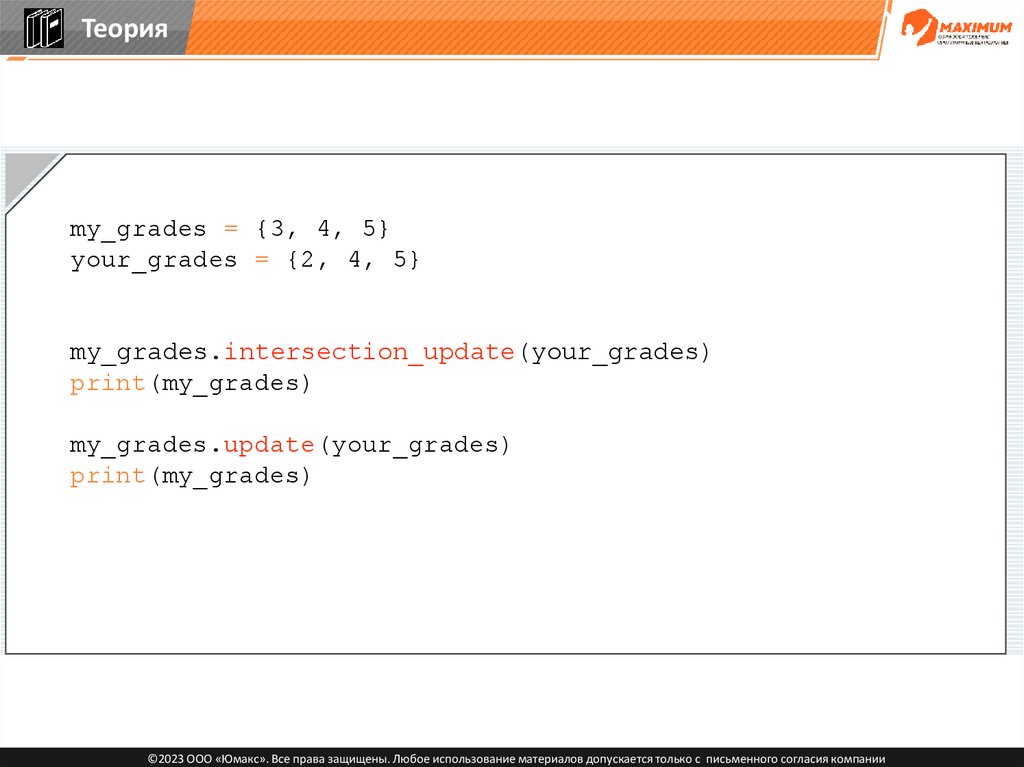
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
84.
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
print(my_grades)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
85.
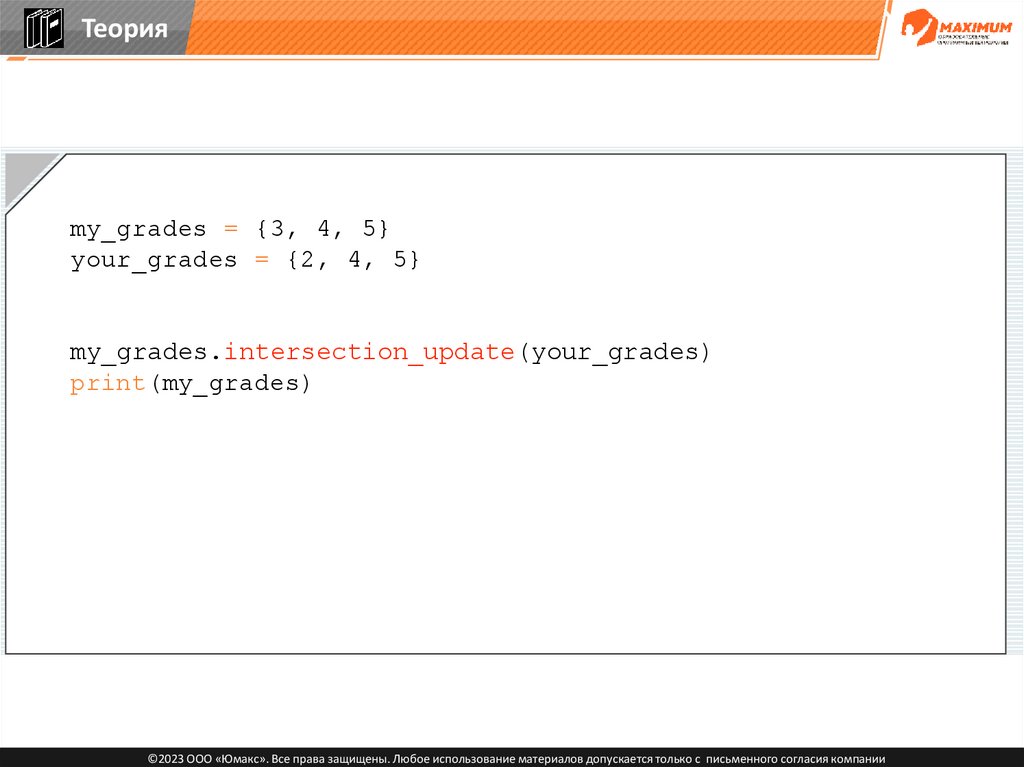
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
print(my_grades)
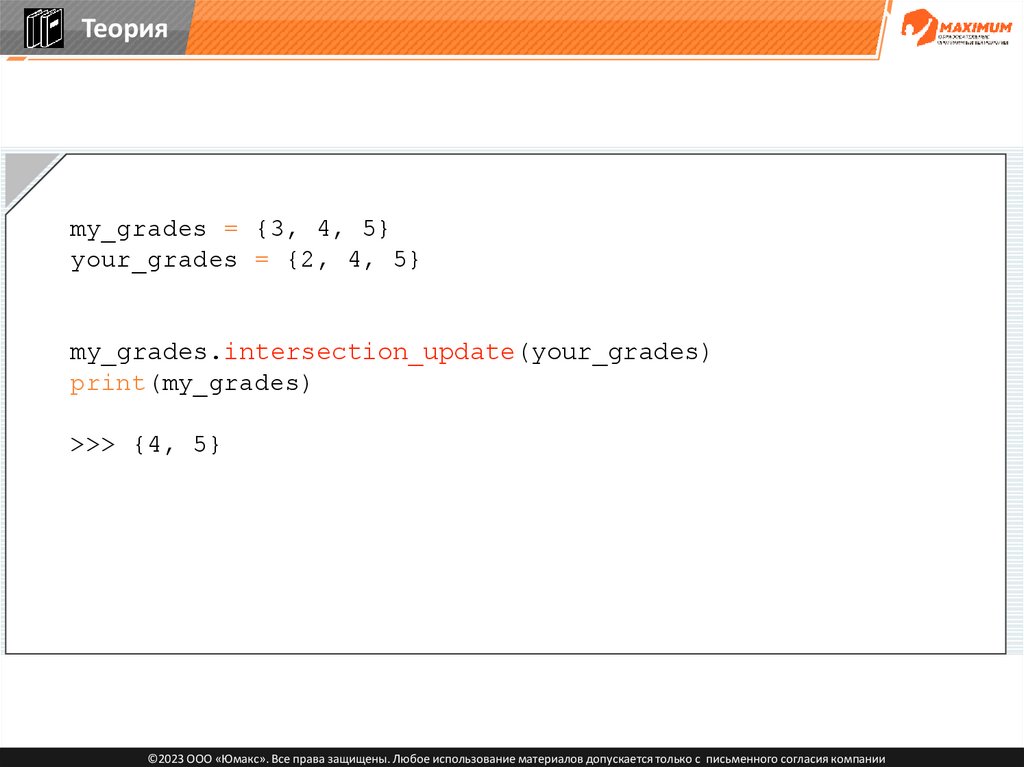
>>> {4, 5}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
86.
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
print(my_grades)
my_grades.update(your_grades)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
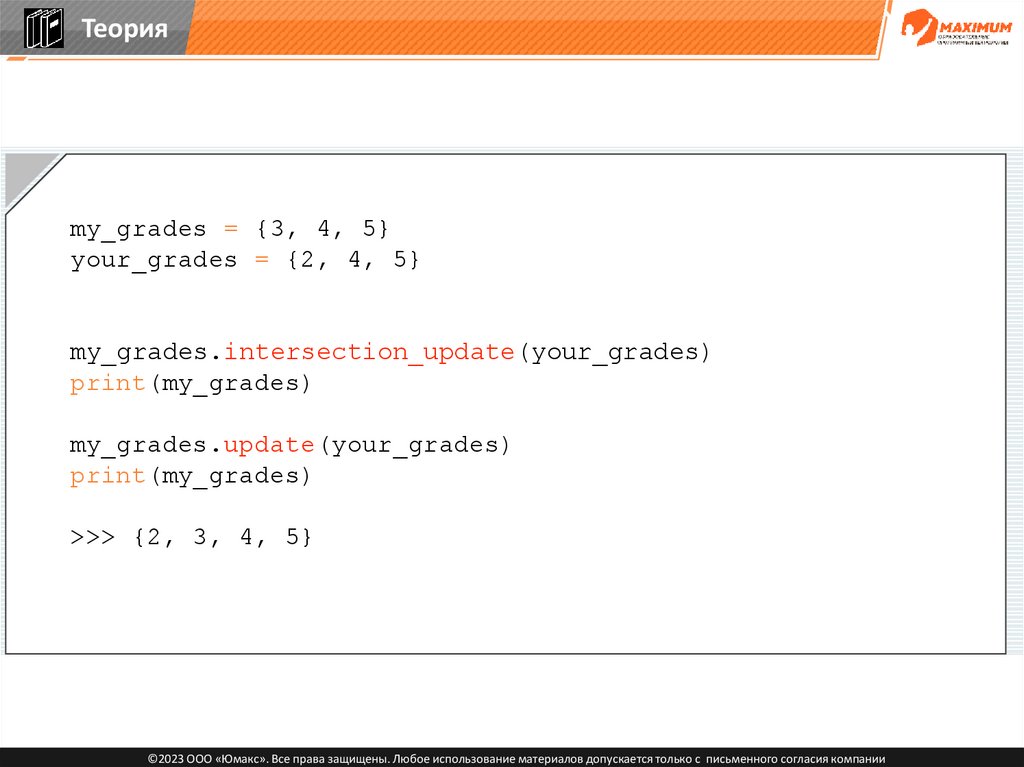
87.
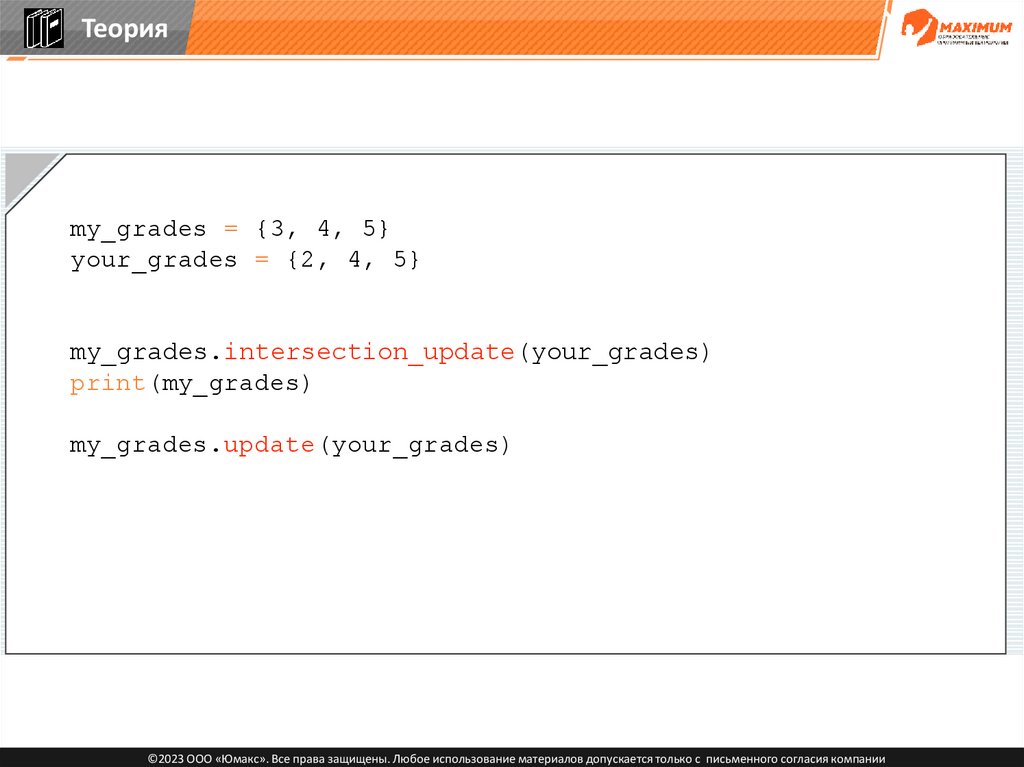
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
print(my_grades)
my_grades.update(your_grades)
print(my_grades)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
88.
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
print(my_grades)
my_grades.update(your_grades)
print(my_grades)
>>> {2, 3, 4, 5}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
89.
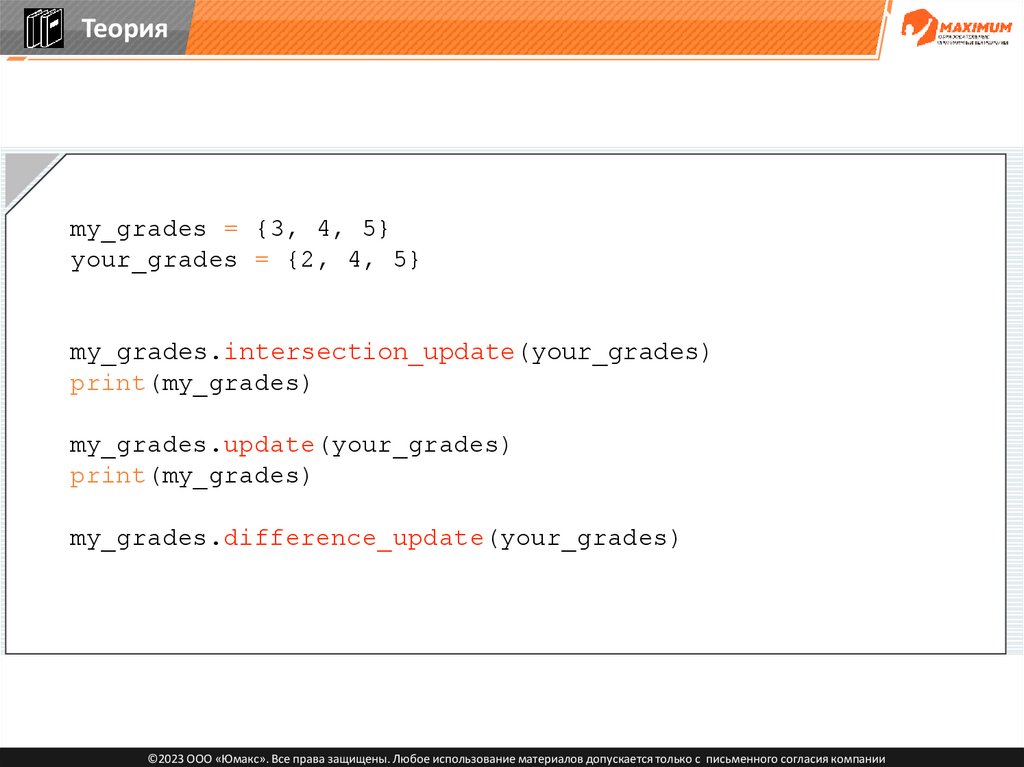
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
print(my_grades)
my_grades.update(your_grades)
print(my_grades)
my_grades.difference_update(your_grades)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
90.
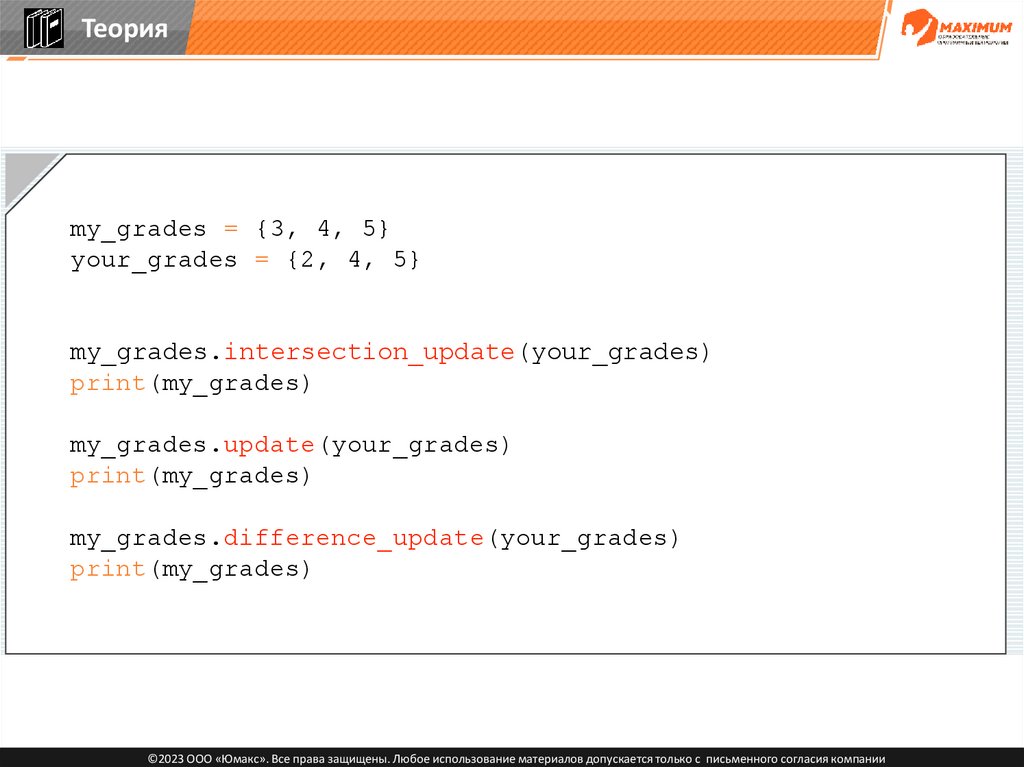
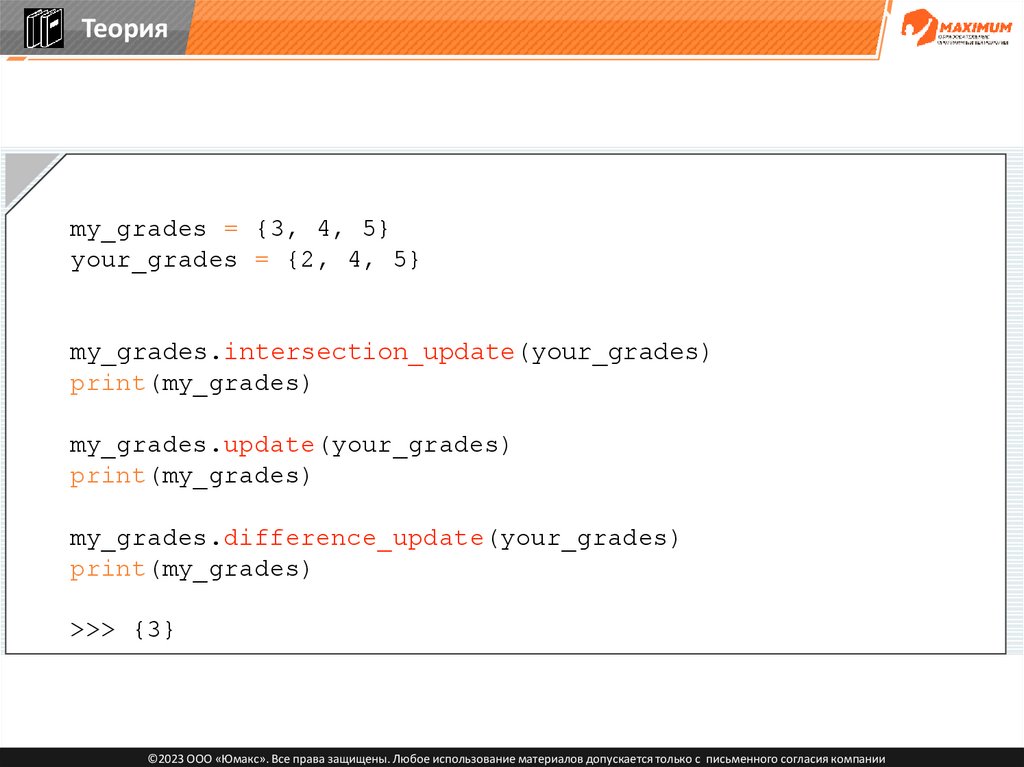
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
print(my_grades)
my_grades.update(your_grades)
print(my_grades)
my_grades.difference_update(your_grades)
print(my_grades)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
91.
Теорияmy_grades = {3, 4, 5}
your_grades = {2, 4, 5}
my_grades.intersection_update(your_grades)
print(my_grades)
my_grades.update(your_grades)
print(my_grades)
my_grades.difference_update(your_grades)
print(my_grades)
>>> {3}
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
92.
ТеорияКейсы применения множеств
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
93.
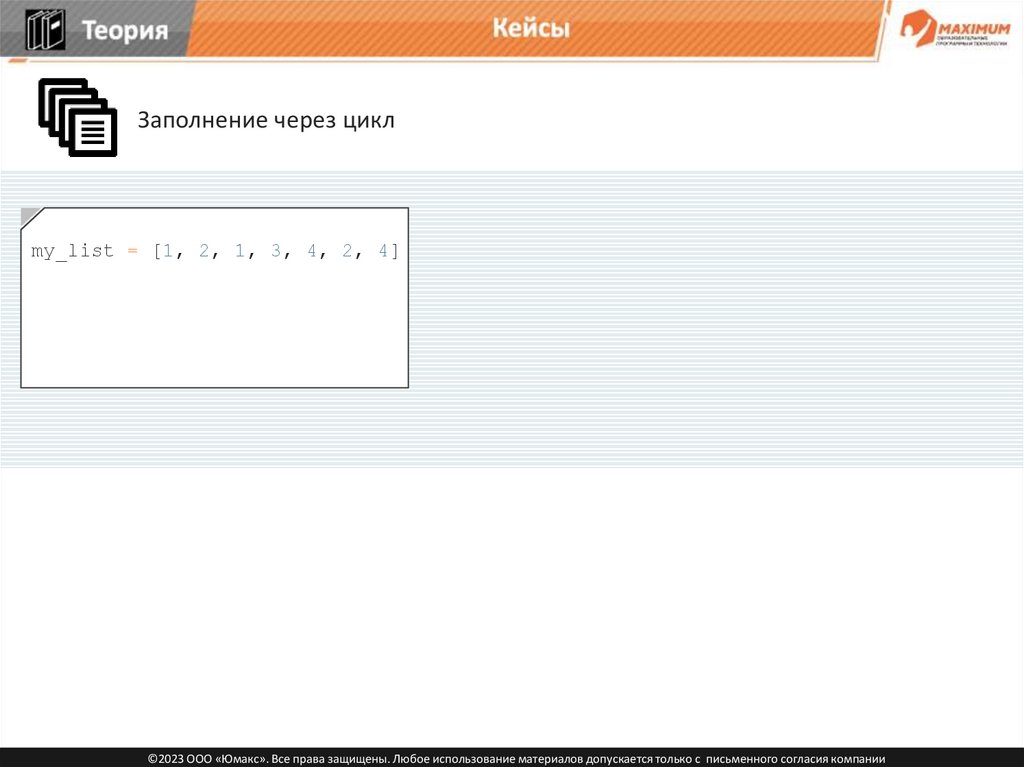
ТеорияКейсы
Заполнение через цикл
my_list = [1, 2, 1, 3, 4, 2, 4]
for i in set(my_list):
print(i)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
94.
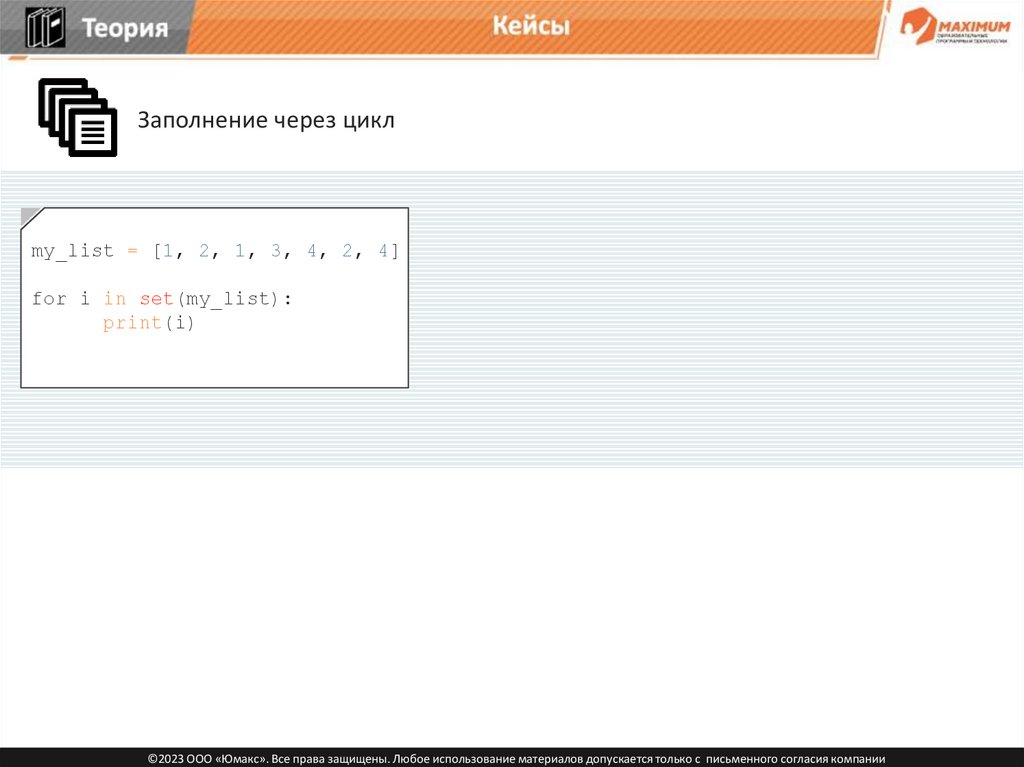
ТеорияКейсы
Заполнение через цикл
my_list = [1, 2, 1, 3, 4, 2, 4]
for i in set(my_list):
print(i)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
95.
ТеорияКейсы
Заполнение через цикл
my_list = [1, 2, 1, 3, 4, 2, 4]
for i in set(my_list):
print(i)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
96.
ТеорияКейсы
Заполнение через цикл
my_list = [1, 2, 1, 3, 4, 2, 4]
for i in set(my_list):
print(i)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
97.
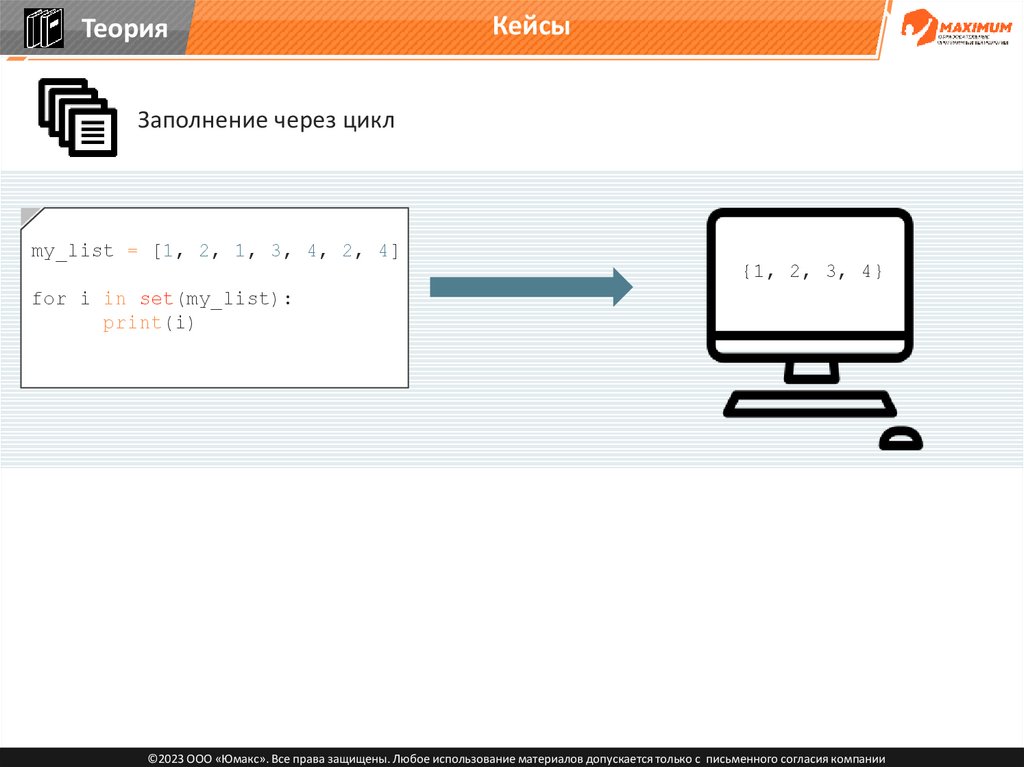
ТеорияКейсы
Заполнение через цикл
my_list = [1, 2, 1, 3, 4, 2, 4]
{1, 2, 3, 4}
for i in set(my_list):
print(i)
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
98.
ТеорияКейсы
Является ли строка 'c a t s' подстрокой
для 'I love cats'?
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
99.
ТеорияКейсы
str1 = 'I love cats'
str2 = 'c a t s'
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
100.
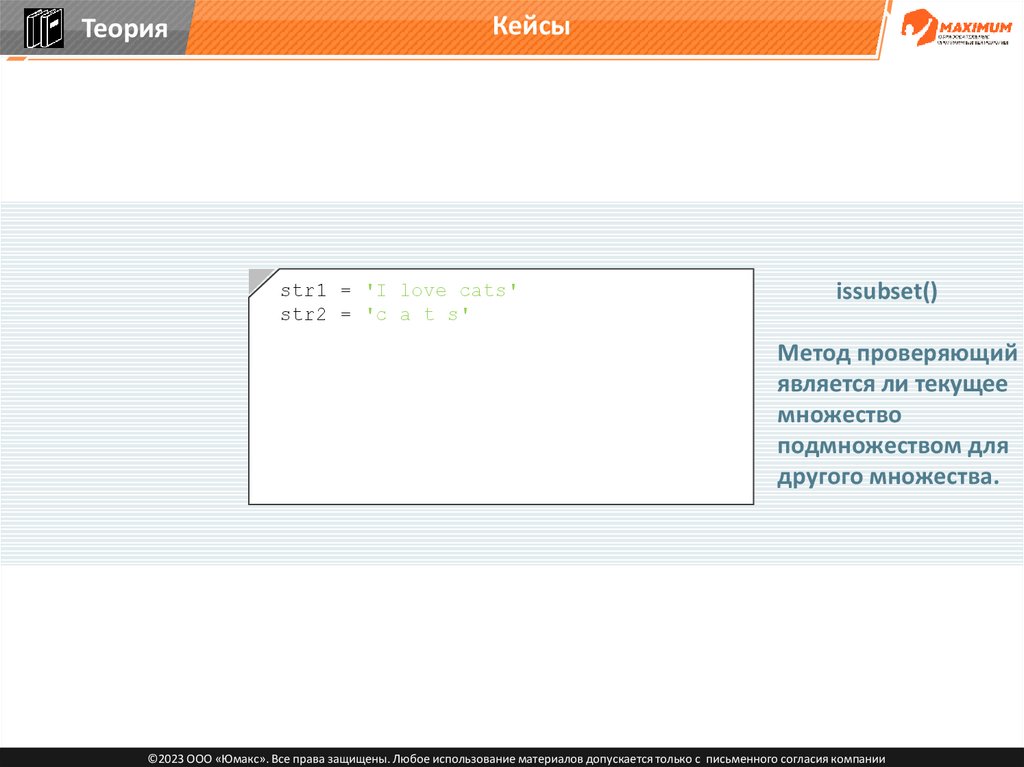
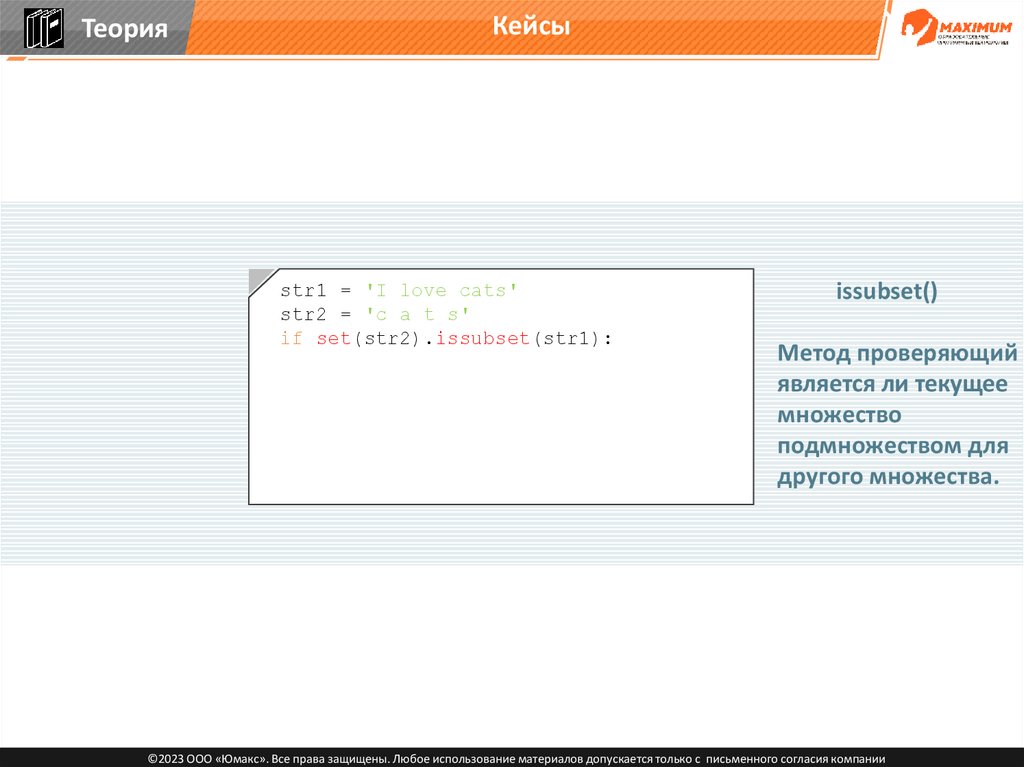
ТеорияКейсы
str1 = 'I love cats'
str2 = 'c a t s'
issubset()
Метод проверяющий
является ли текущее
множество
подмножеством для
другого множества.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
101.
ТеорияКейсы
str1 = 'I love cats'
str2 = 'c a t s'
if set(str2).issubset(str1):
issubset()
Метод проверяющий
является ли текущее
множество
подмножеством для
другого множества.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
102.
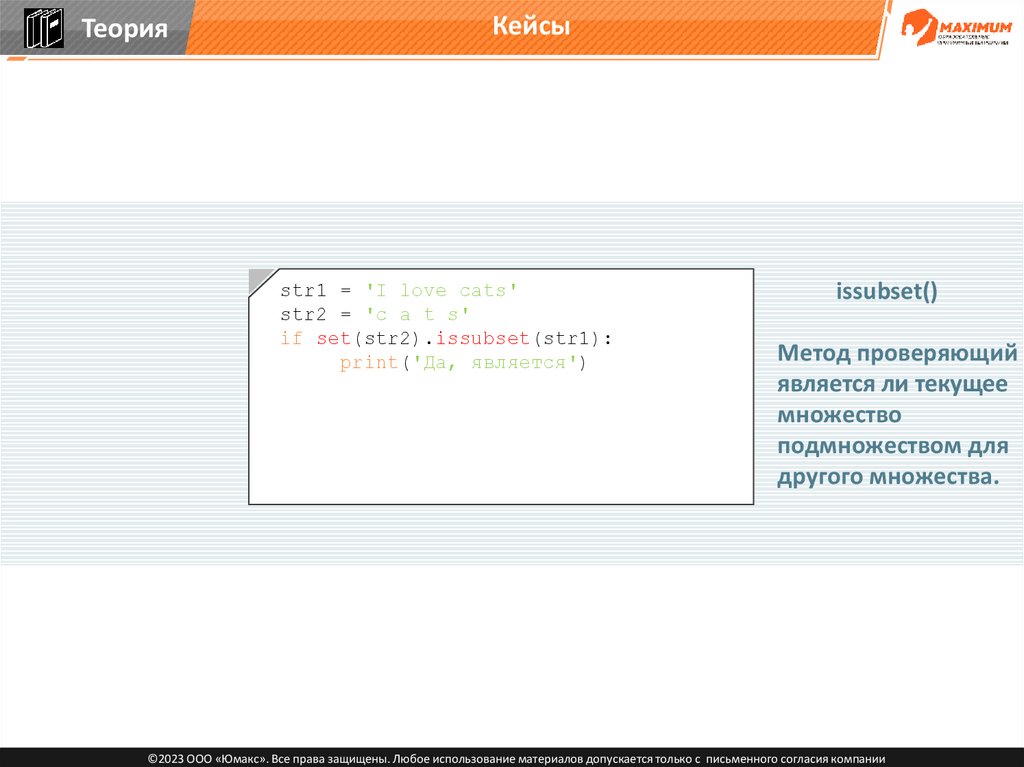
ТеорияКейсы
str1 = 'I love cats'
str2 = 'c a t s'
if set(str2).issubset(str1):
print('Да, является')
issubset()
Метод проверяющий
является ли текущее
множество
подмножеством для
другого множества.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
103.
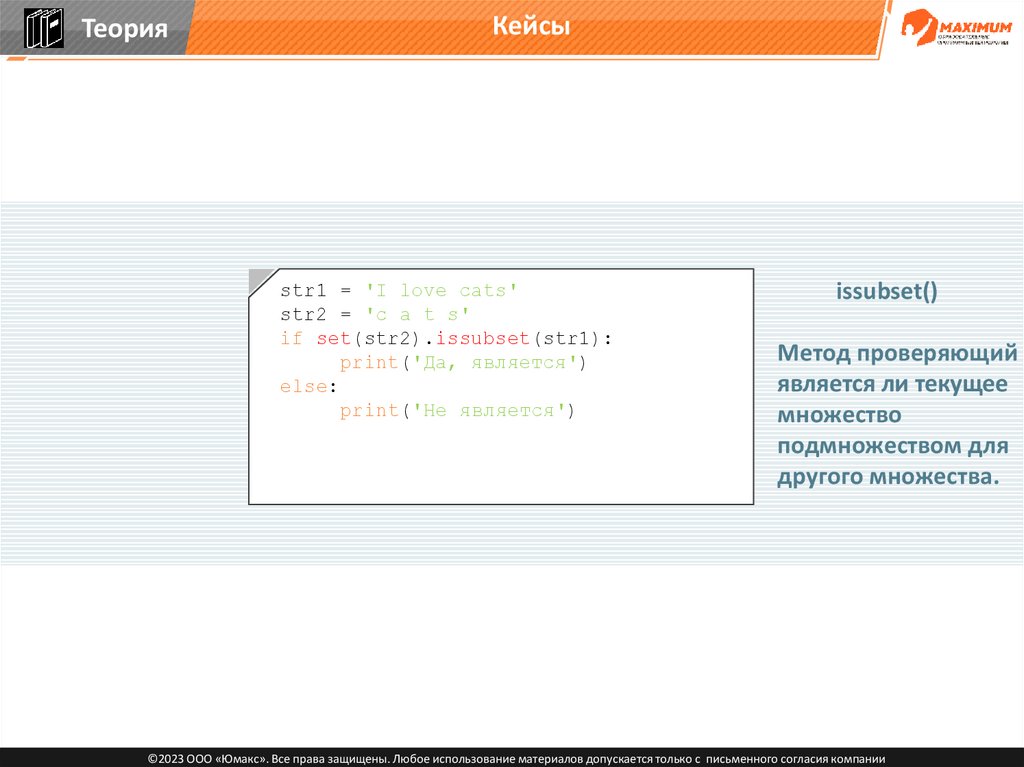
ТеорияКейсы
str1 = 'I love cats'
str2 = 'c a t s'
if set(str2).issubset(str1):
print('Да, является')
else:
print('Не является')
issubset()
Метод проверяющий
является ли текущее
множество
подмножеством для
другого множества.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
104.
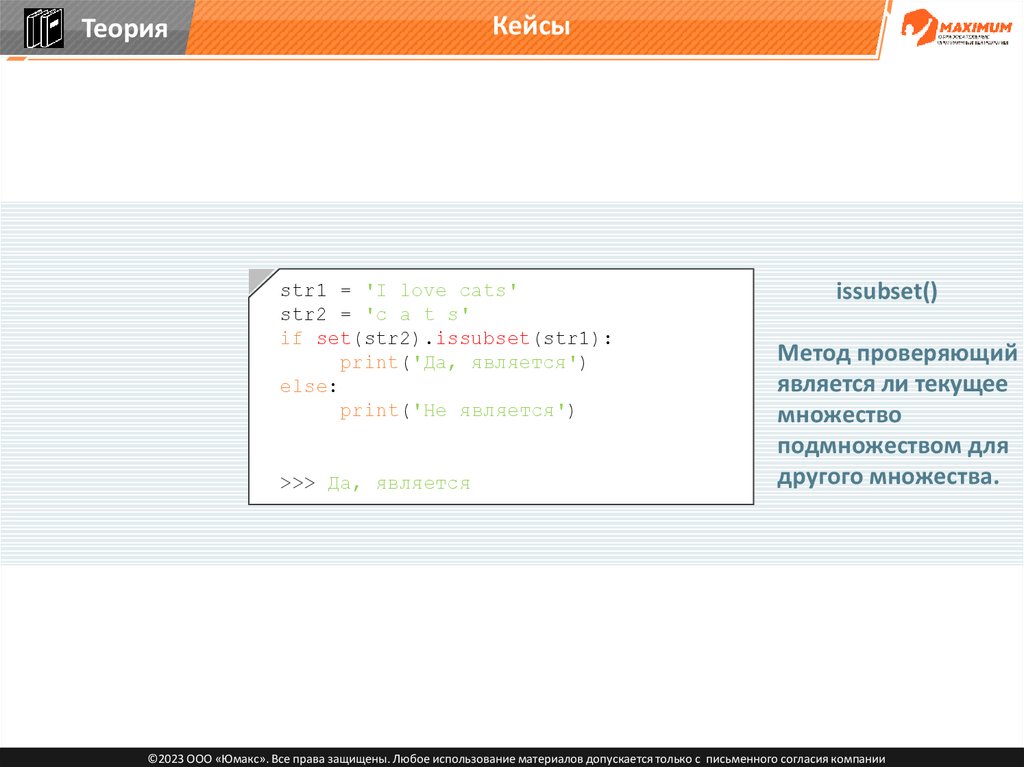
КейсыТеория
str1 = 'I love cats'
str2 = 'c a t s'
if set(str2).issubset(str1):
print('Да, является')
else:
print('Не является')
>>> Да, является
issubset()
Метод проверяющий
является ли текущее
множество
подмножеством для
другого множества.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
105.
ТеорияПетя и Ваня играют в игру. Петя загадал натуральное число в
диапазоне от 1 до n включительно. Ваня пытается угадать это число,
для этого он называет некоторые множества натуральных чисел.
Петя отвечает Ване YES, если среди названных чисел есть задуманное
или NO в противном случае.
После нескольких заданных вопросов Ваня запутался в том, какие
вопросы он задавал и какие ответы получил, в связи с чем просит вас
помочь ему определить, какие числа мог загадать Петя.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
106.
ТеорияФормат входных данных
Первая строка входных данных содержит число натуральное n —
наибольшее число, которое мог загадать Петя. Далее идут строки,
которые являются вариантами ответа Вани. Каждая строка
представляет собой набор натуральных чисел, разделенных
пробелами. После каждой строки с вопросом вводится с клавиатуры
ответ Пети: YES или NO. Наконец, последняя строка входных данных
содержит одно слово HELP.
Формат выходных данных
Вы должны вывести все числа, которые мог бы загадать Петя, исходя
из указанных входных данных.
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
107.
ТеорияПример входных данных:
10
12345
YES
24
NO
HELP
Пример выходных данных:
135
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
108.
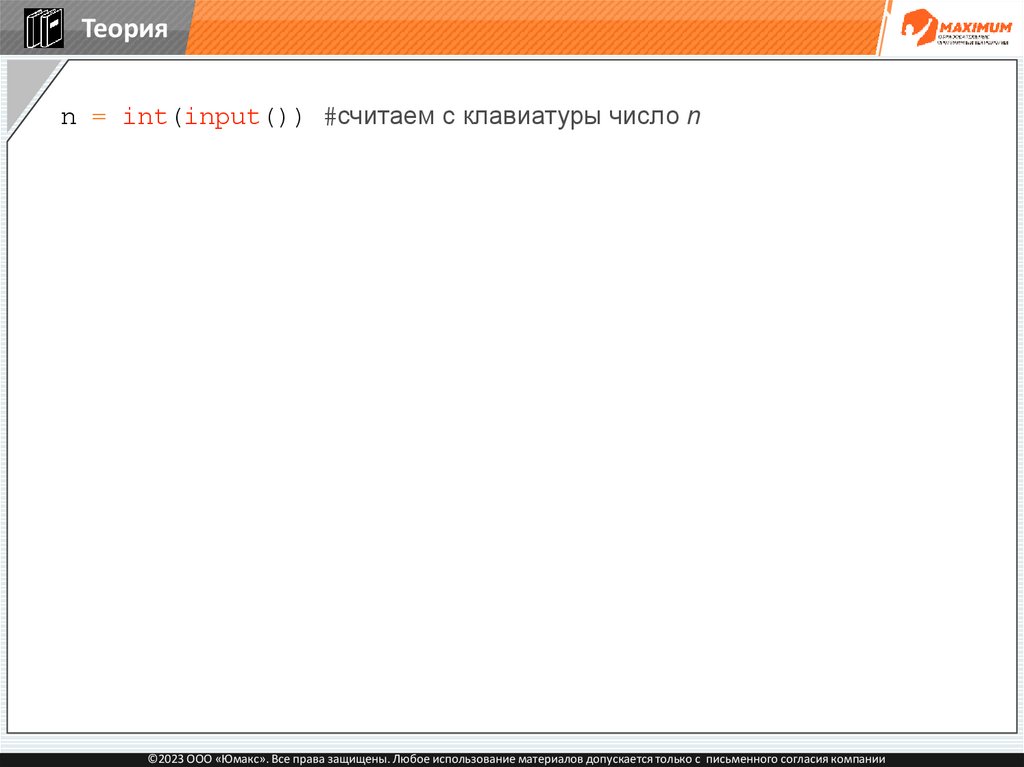
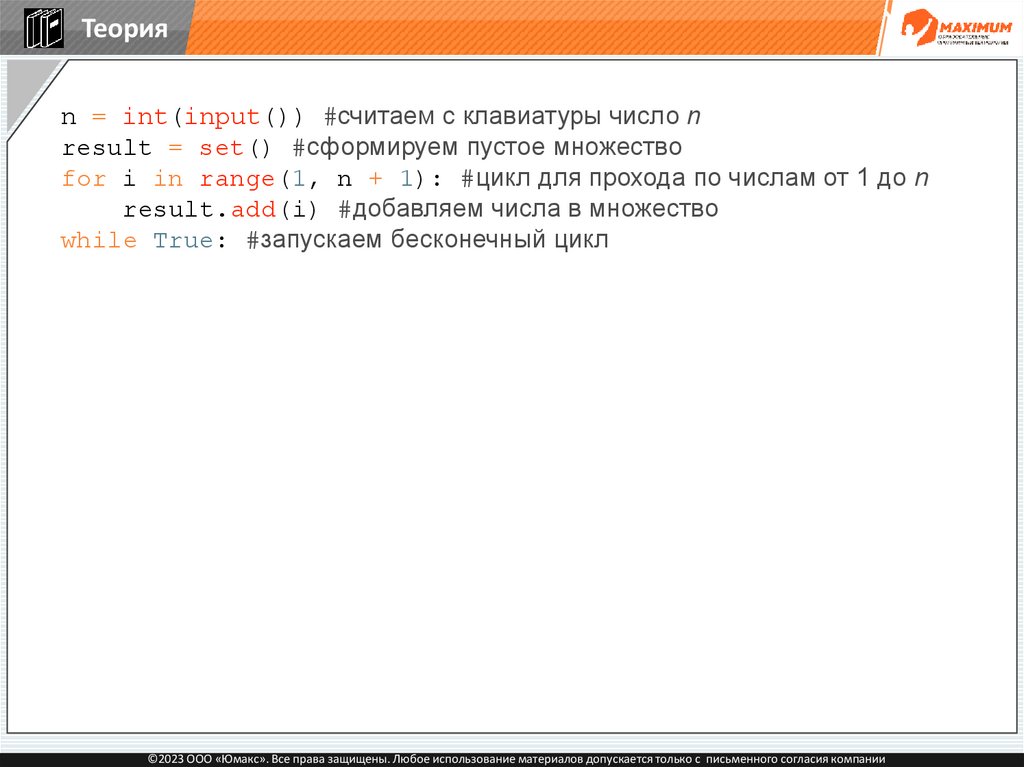
Теорияn = int(input()) #считаем с клавиатуры число n
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
109.
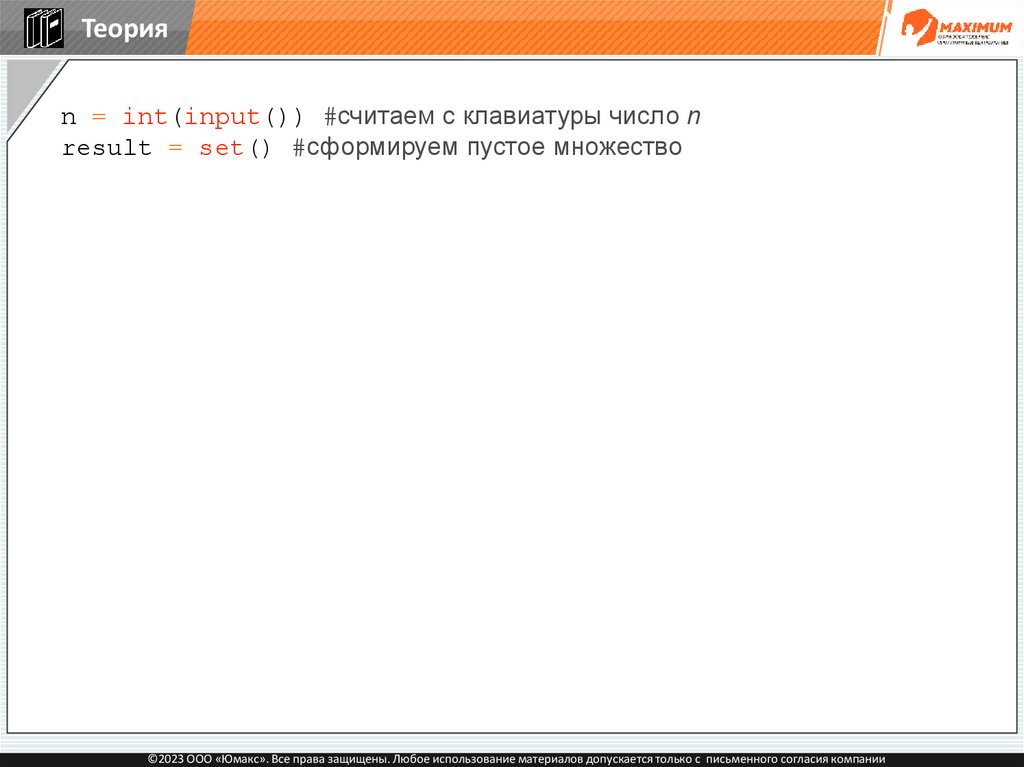
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
110.
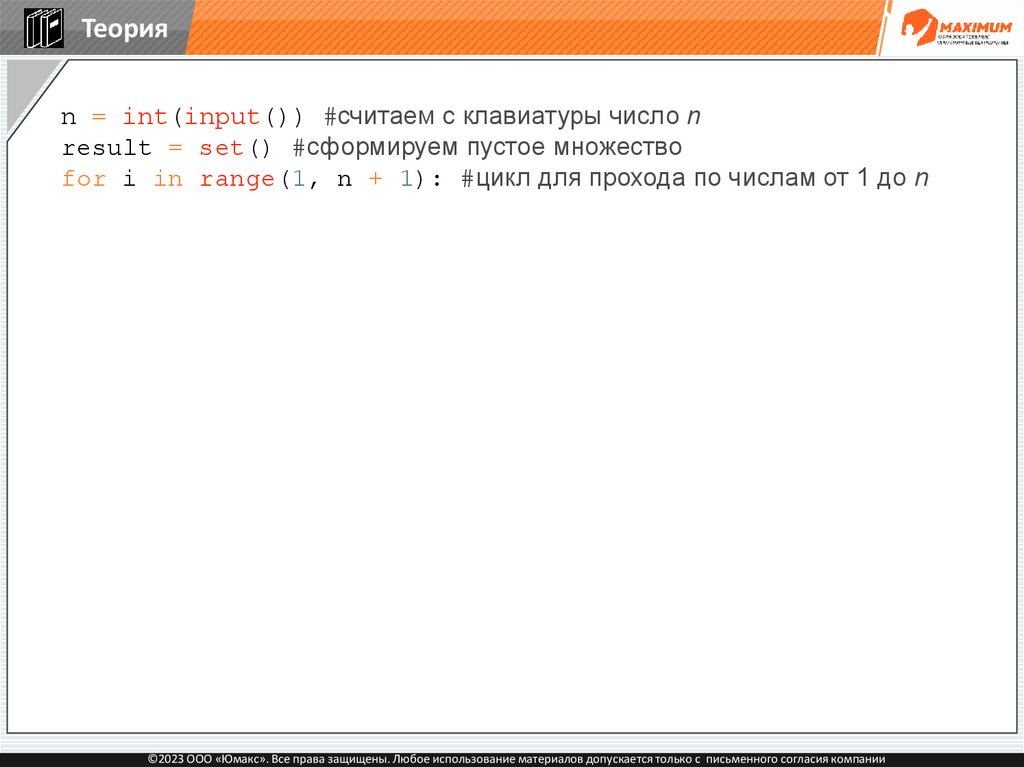
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
111.
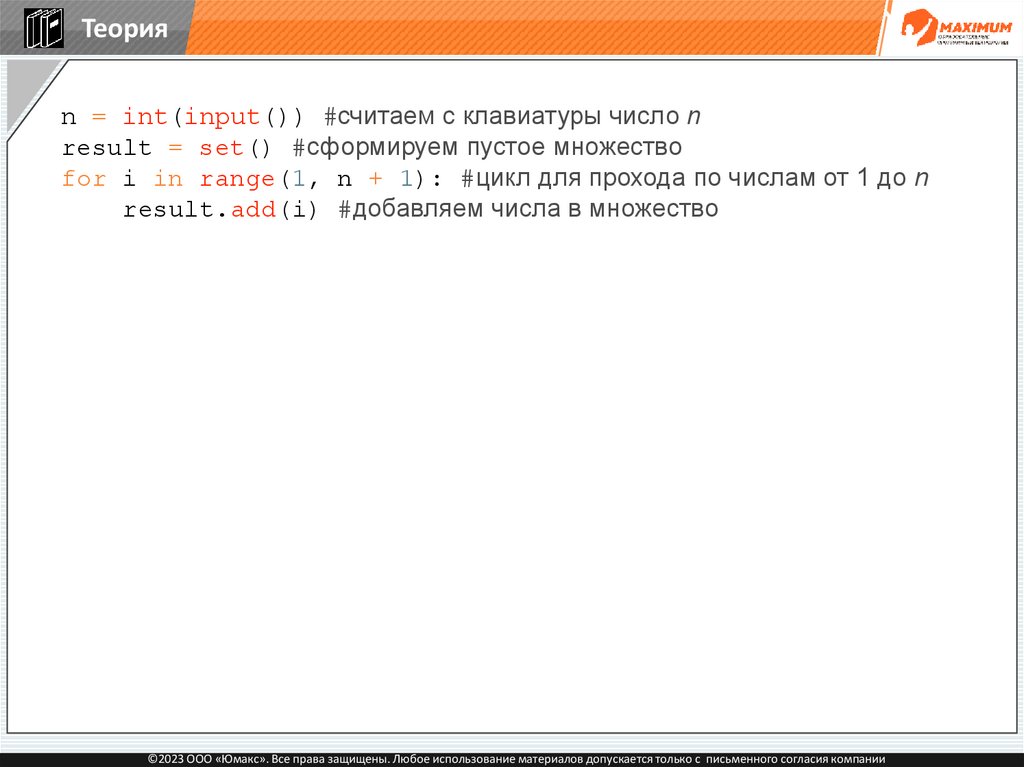
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
112.
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
113.
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
114.
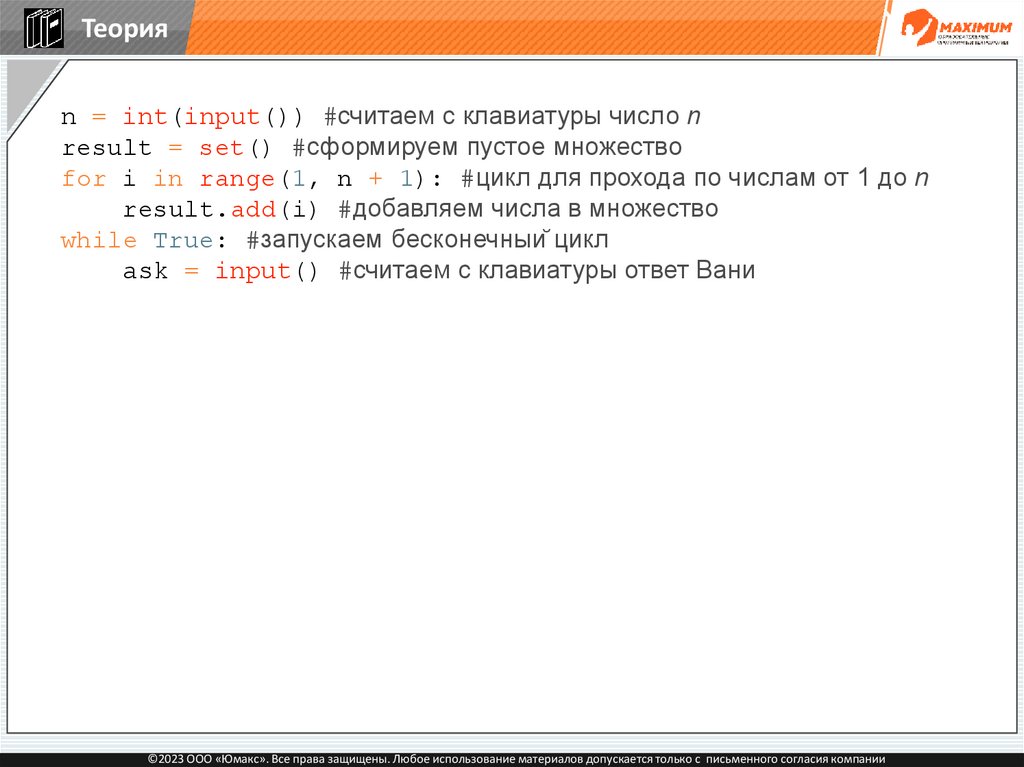
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
115.
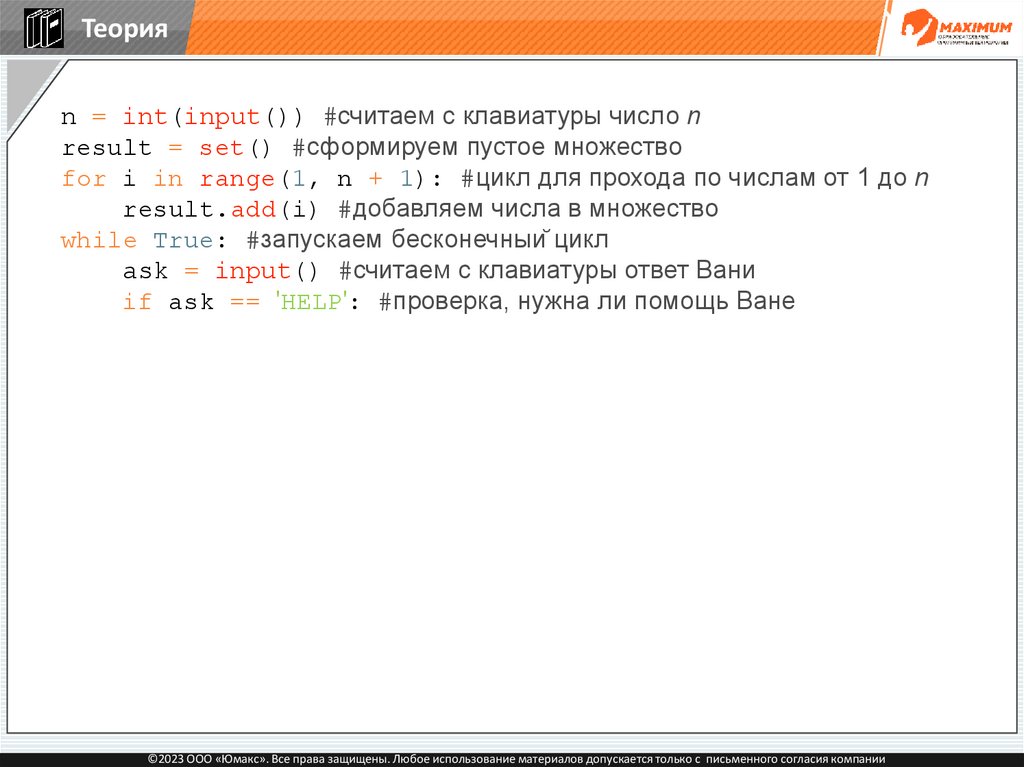
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
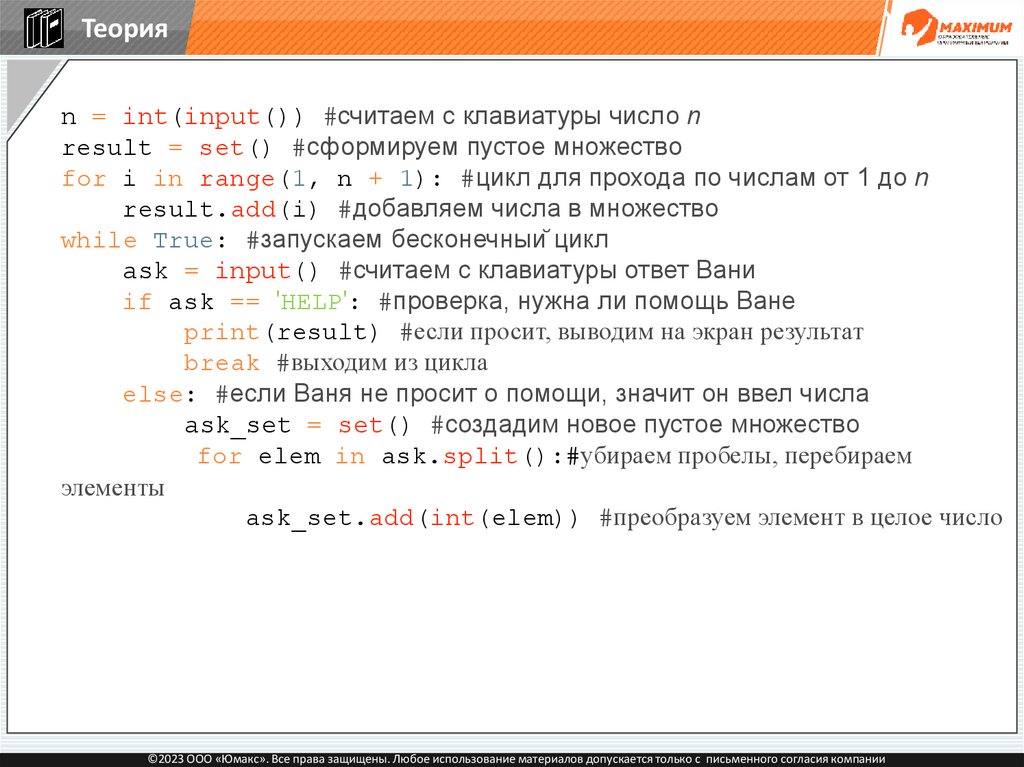
116.
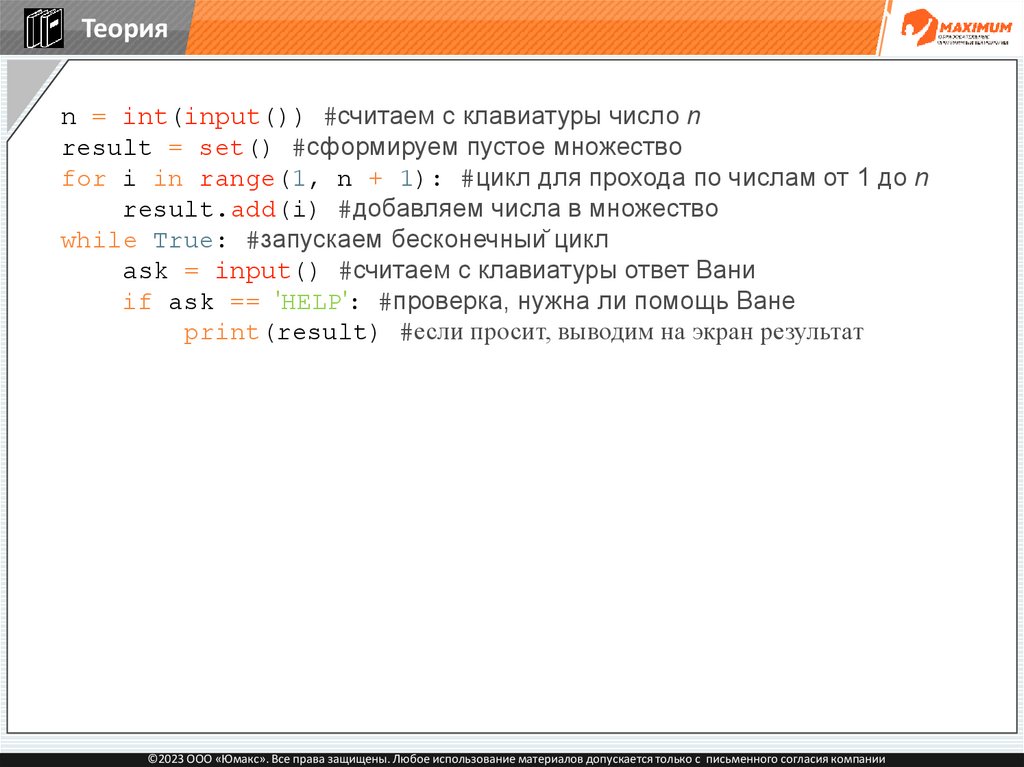
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
117.
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
118.
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
ask_set = set() #создадим новое пустое множество
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
119.
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
ask_set = set() #создадим новое пустое множество
for elem in ask.split():#убираем пробелы, перебираем
элементы
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
120.
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
ask_set = set() #создадим новое пустое множество
for elem in ask.split():#убираем пробелы, перебираем
элементы
ask_set.add(int(elem)) #преобразуем элемент в целое число
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
121.
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
ask_set = set() #создадим новое пустое множество
for elem in ask.split():#убираем пробелы, перебираем
элементы
ask_set.add(int(elem)) #преобразуем элемент в целое число
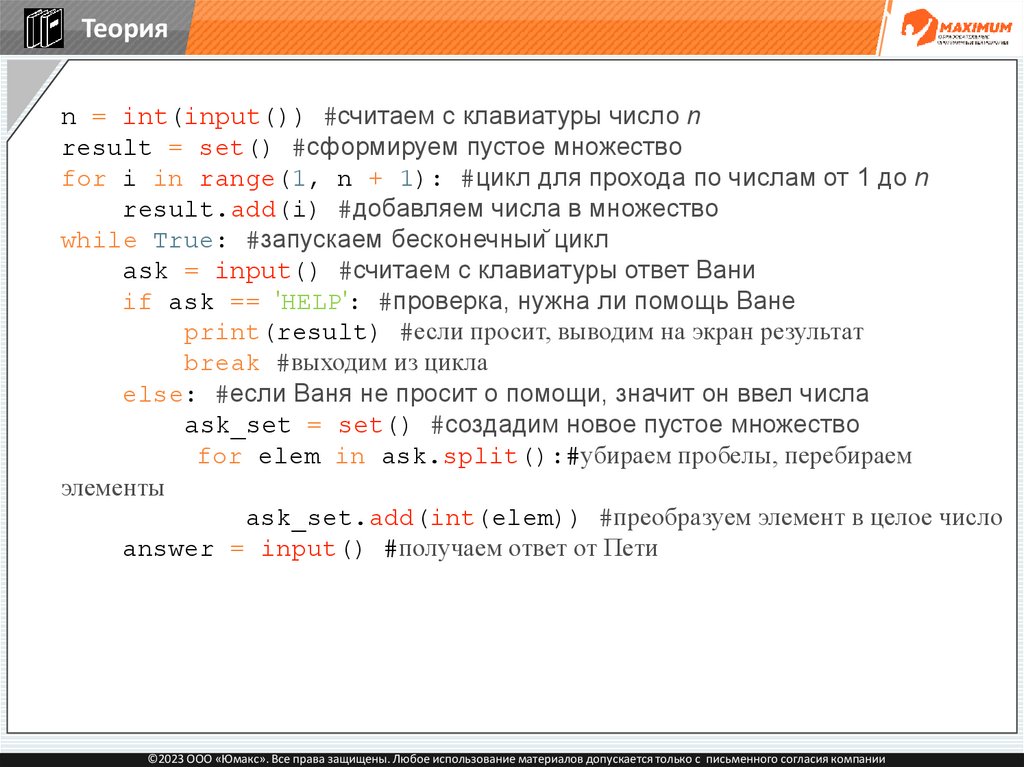
answer = input() #получаем ответ от Пети
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
122.
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
ask_set = set() #создадим новое пустое множество
for elem in ask.split():#убираем пробелы, перебираем
элементы
ask_set.add(int(elem)) #преобразуем элемент в целое число
answer = input() #получаем ответ от Пети
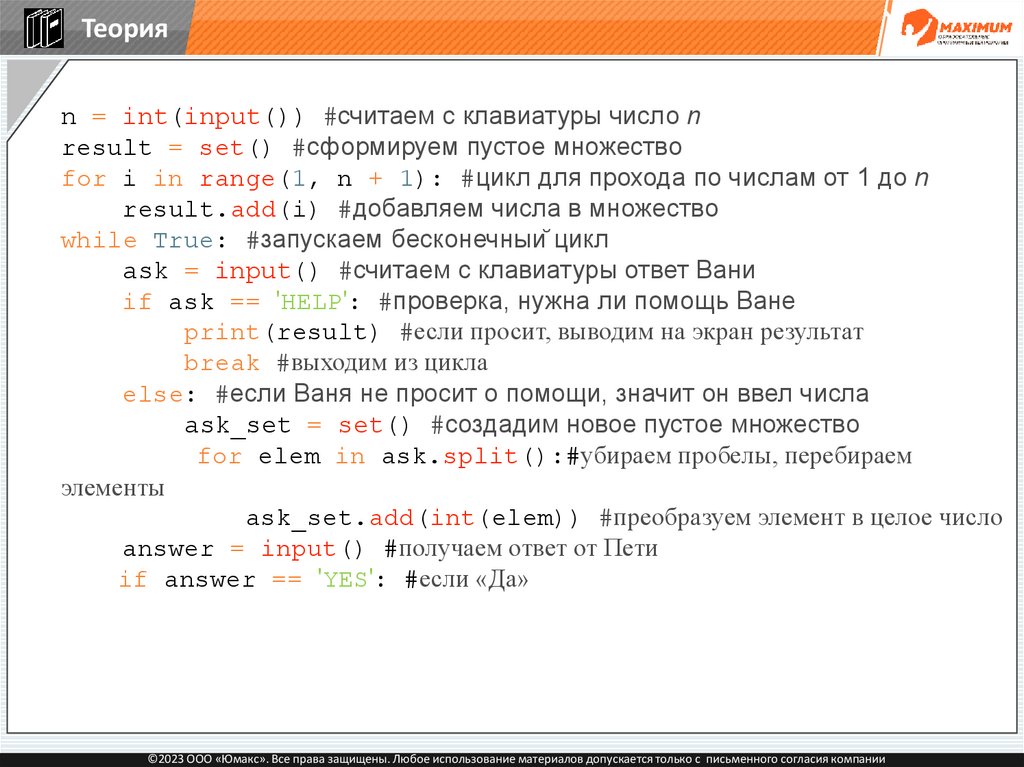
if answer == 'YES': #если «Да»
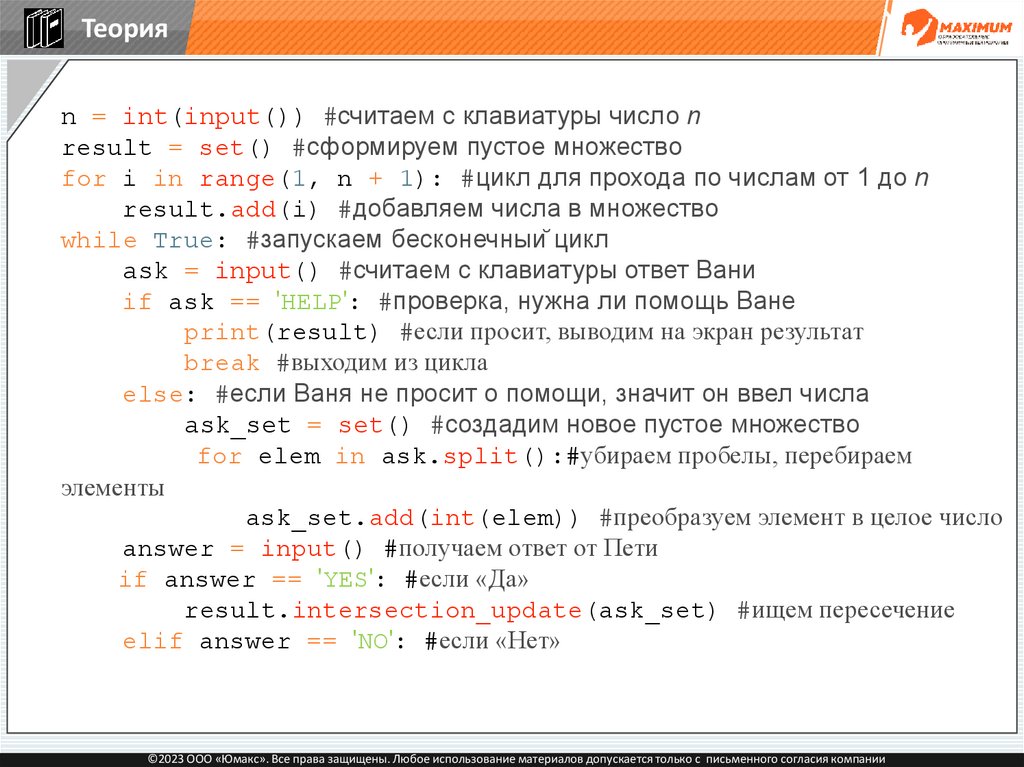
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
123.
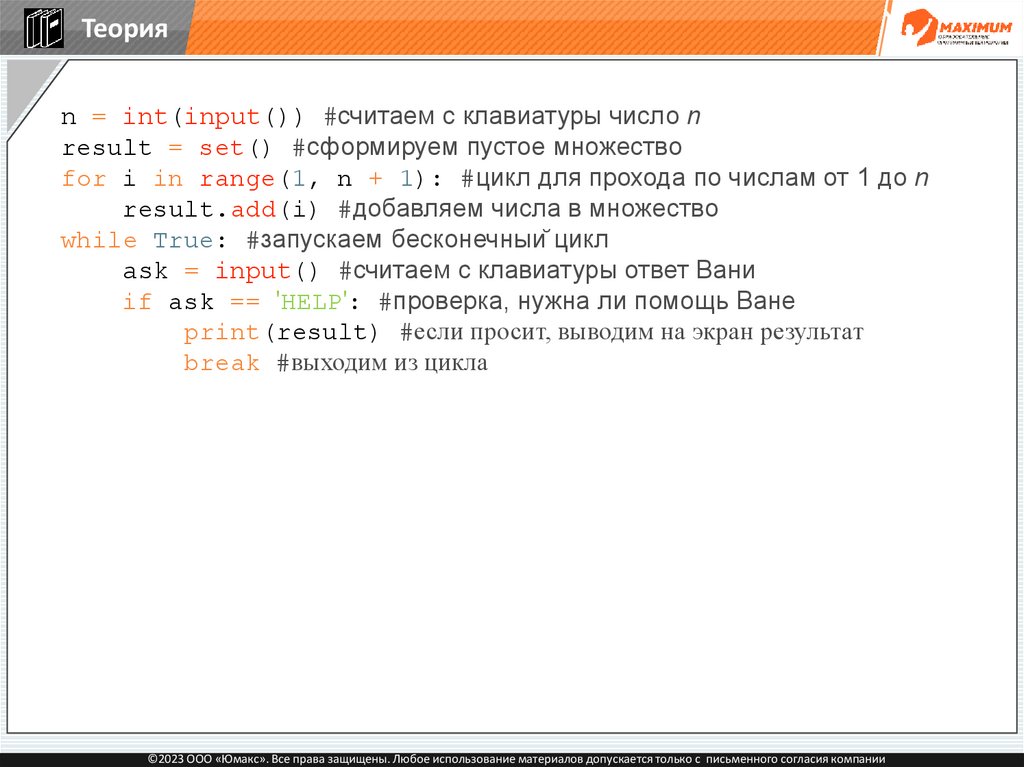
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
ask_set = set() #создадим новое пустое множество
for elem in ask.split():#убираем пробелы, перебираем
элементы
ask_set.add(int(elem)) #преобразуем элемент в целое число
answer = input() #получаем ответ от Пети
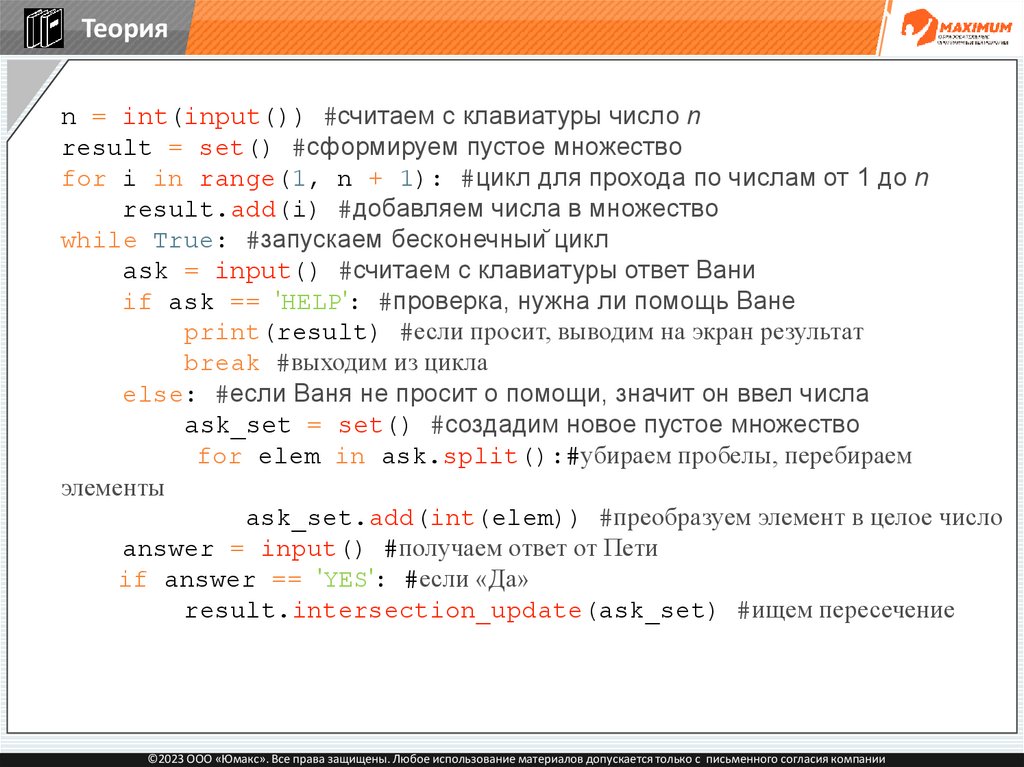
if answer == 'YES': #если «Да»
result.intersection_update(ask_set) #ищем пересечение
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
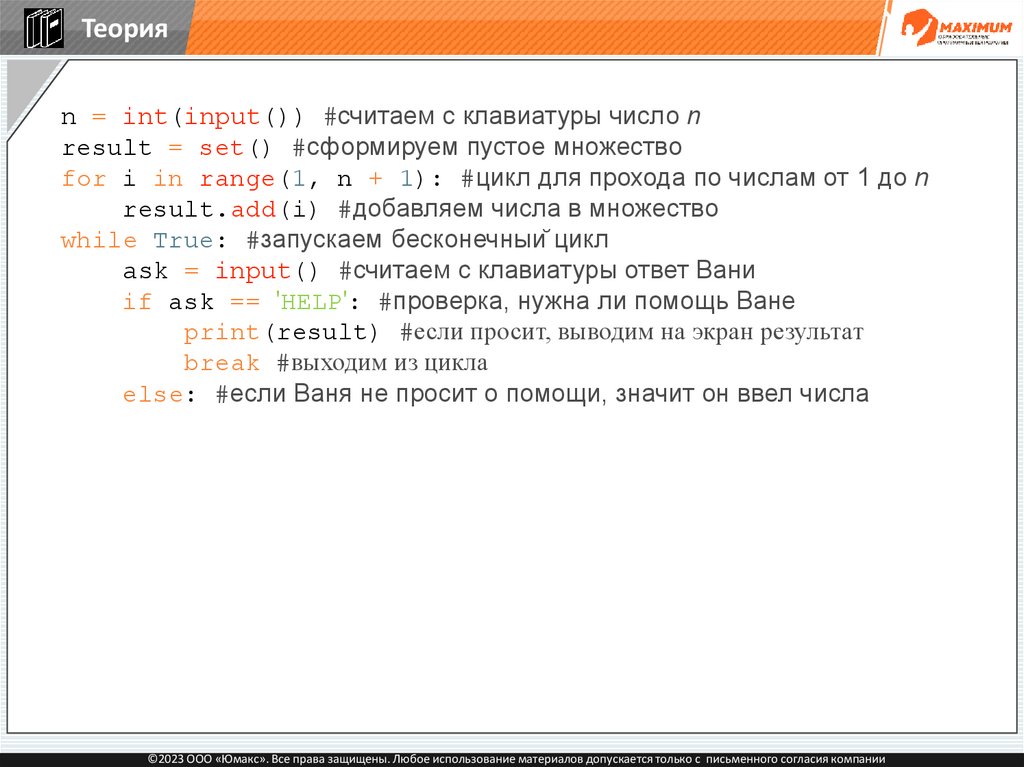
124.
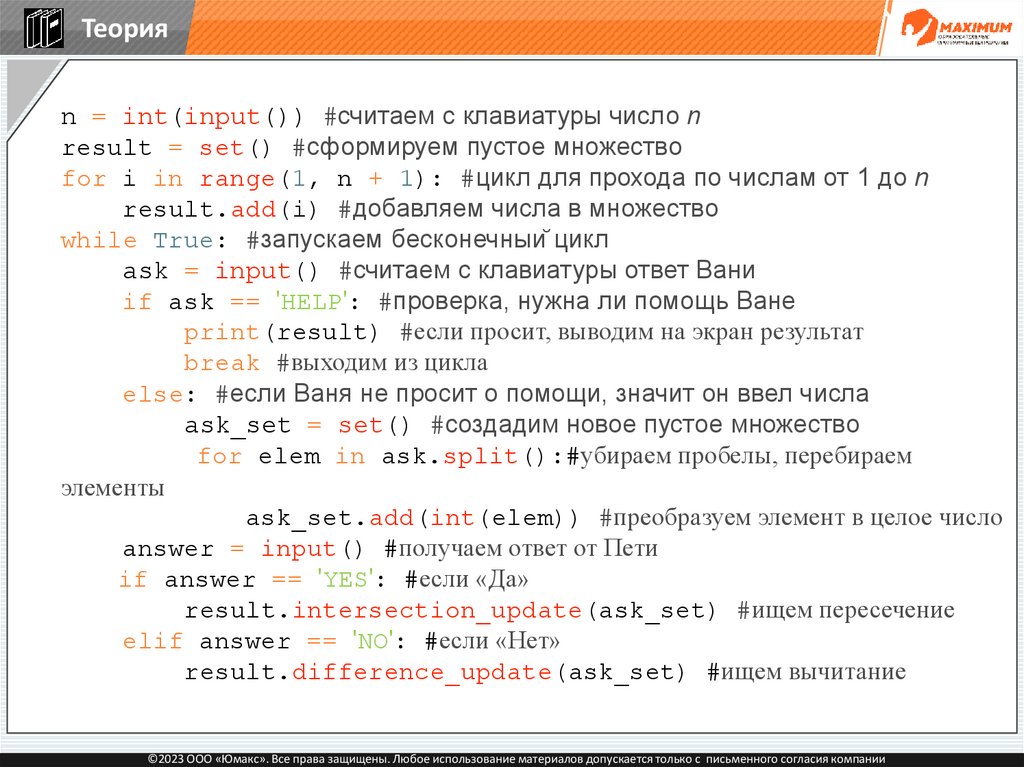
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
ask_set = set() #создадим новое пустое множество
for elem in ask.split():#убираем пробелы, перебираем
элементы
ask_set.add(int(elem)) #преобразуем элемент в целое число
answer = input() #получаем ответ от Пети
if answer == 'YES': #если «Да»
result.intersection_update(ask_set) #ищем пересечение
elif answer == 'NO': #если «Нет»
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
125.
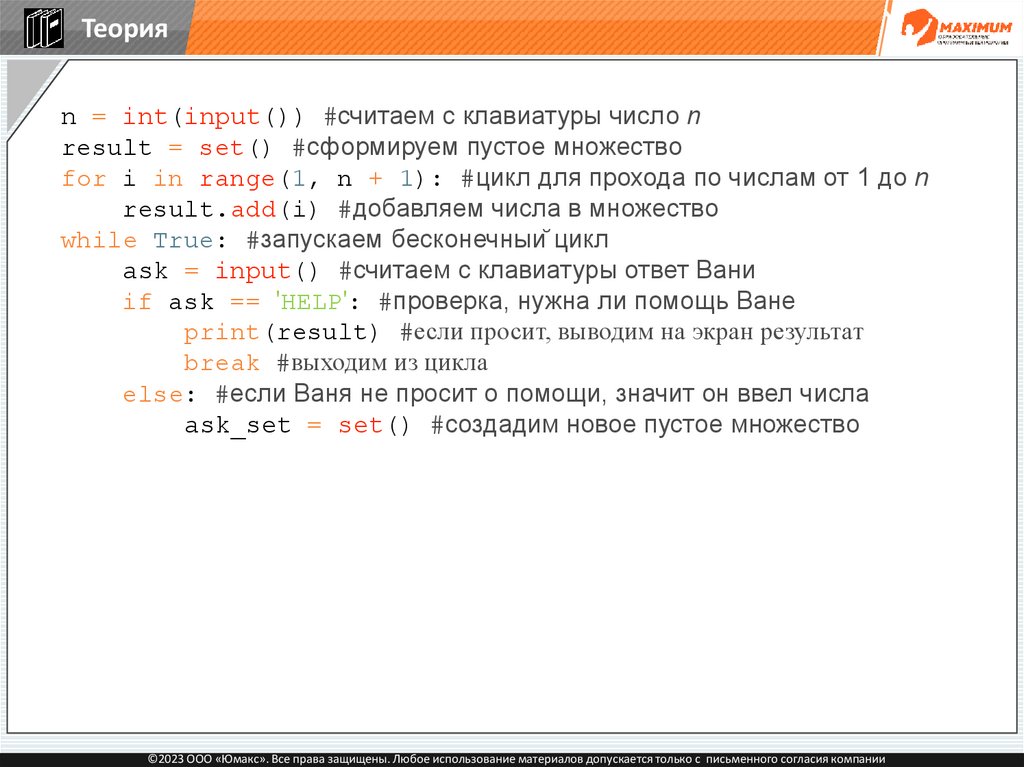
Теорияn = int(input()) #считаем с клавиатуры число n
result = set() #сформируем пустое множество
for i in range(1, n + 1): #цикл для прохода по числам от 1 до n
result.add(i) #добавляем числа в множество
while True: #запускаем бесконечный цикл
ask = input() #считаем с клавиатуры ответ Вани
if ask == 'HELP': #проверка, нужна ли помощь Ване
print(result) #если просит, выводим на экран результат
break #выходим из цикла
else: #если Ваня не просит о помощи, значит он ввел числа
ask_set = set() #создадим новое пустое множество
for elem in ask.split():#убираем пробелы, перебираем
элементы
ask_set.add(int(elem)) #преобразуем элемент в целое число
answer = input() #получаем ответ от Пети
if answer == 'YES': #если «Да»
result.intersection_update(ask_set) #ищем пересечение
elif answer == 'NO': #если «Нет»
result.difference_update(ask_set) #ищем вычитание
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
126.
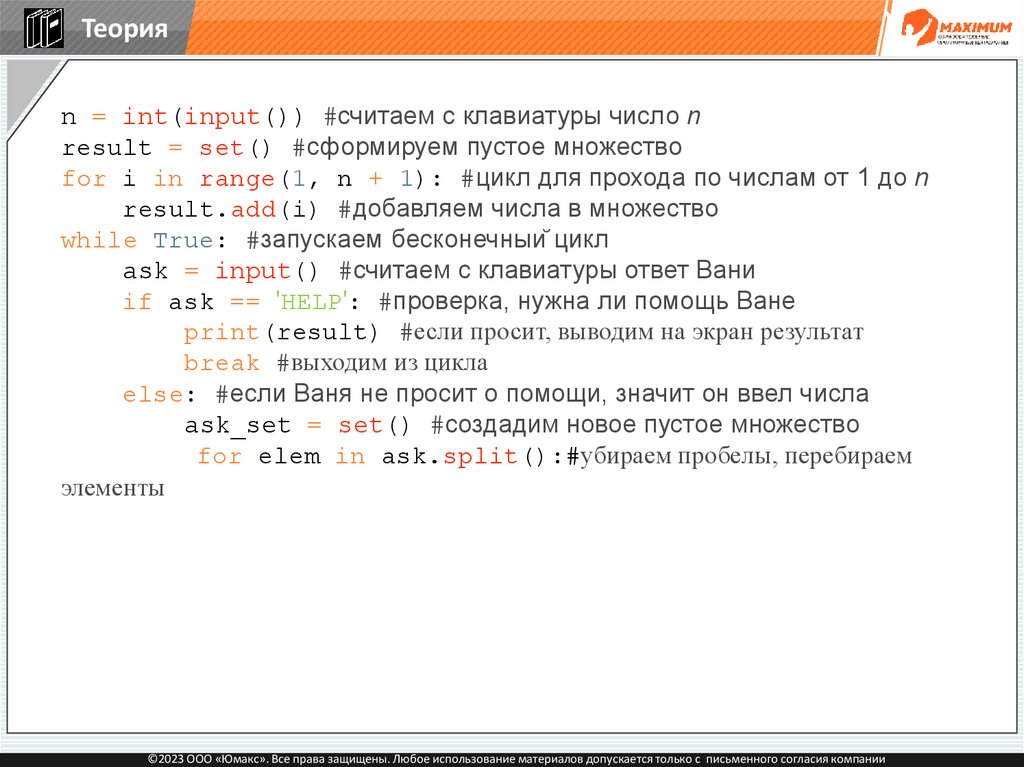
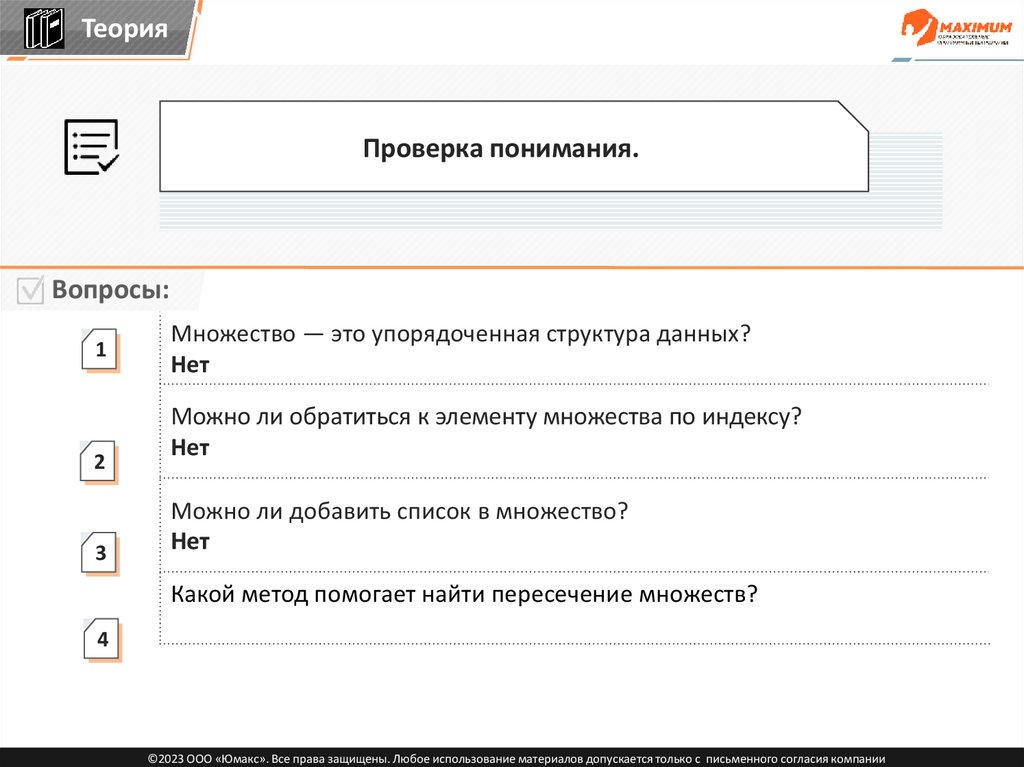
Теория2
Проверка понимания.
Вопросы:
1
Множество — это упорядоченная структура данных?
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
127.
Теория2
Проверка понимания.
Вопросы:
1
Множество — это упорядоченная структура данных?
Нет
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
128.
Теория2
Проверка понимания.
Вопросы:
1
Множество — это упорядоченная структура данных?
Нет
Можно ли обратиться к элементу множества по индексу?
2
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
129.
Теория2
Проверка понимания.
Вопросы:
1
2
Множество — это упорядоченная структура данных?
Нет
Можно ли обратиться к элементу множества по индексу?
Нет
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
130.
Теория2
Проверка понимания.
Вопросы:
1
2
3
Множество — это упорядоченная структура данных?
Нет
Можно ли обратиться к элементу множества по индексу?
Нет
Можно ли добавить список в множество?
Нет
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
131.
Теория2
Проверка понимания.
Вопросы:
1
2
3
Множество — это упорядоченная структура данных?
Нет
Можно ли обратиться к элементу множества по индексу?
Нет
Можно ли добавить список в множество?
Нет
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
132.
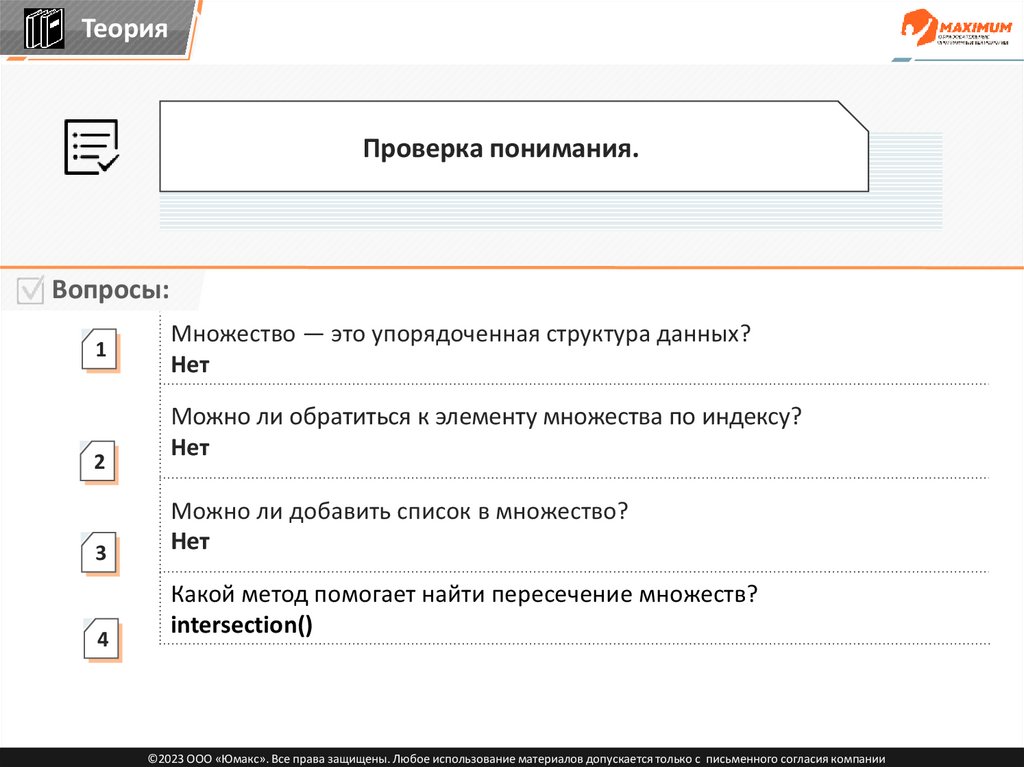
Теория2
Проверка понимания.
Вопросы:
1
2
3
4
Множество — это упорядоченная структура данных?
Нет
Можно ли обратиться к элементу множества по индексу?
Нет
Можно ли добавить список в множество?
Нет
Какой метод помогает найти пересечение множеств?
intersection()
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
133.
Теория2
Проверка понимания.
Вопросы:
1
2
3
4
Множество — это упорядоченная структура данных?
Нет
Можно ли обратиться к элементу множества по индексу?
Нет
Можно ли добавить список в множество?
Нет
Какой метод помогает найти пересечение множеств?
intersection()
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
134.
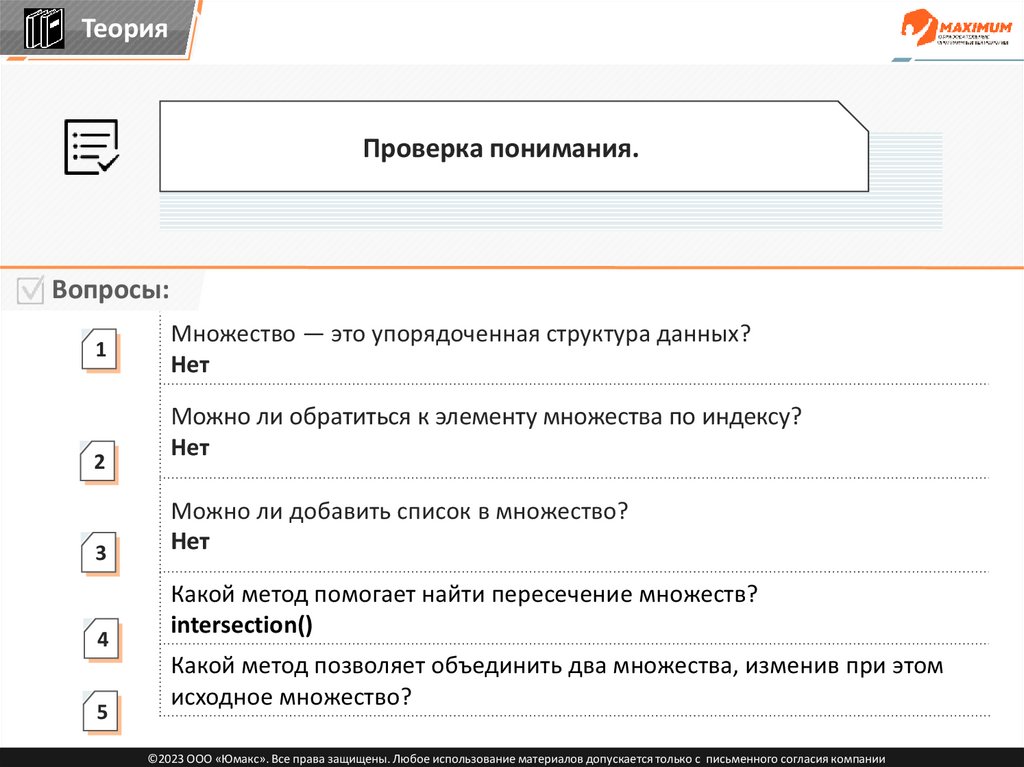
Теория2
Проверка понимания.
Вопросы:
1
2
3
4
5
Множество — это упорядоченная структура данных?
Нет
Можно ли обратиться к элементу множества по индексу?
Нет
Можно ли добавить список в множество?
Нет
Какой метод помогает найти пересечение множеств?
intersection()
Какой метод позволяет объединить два множества, изменив при этом
исходное множество?
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
135.
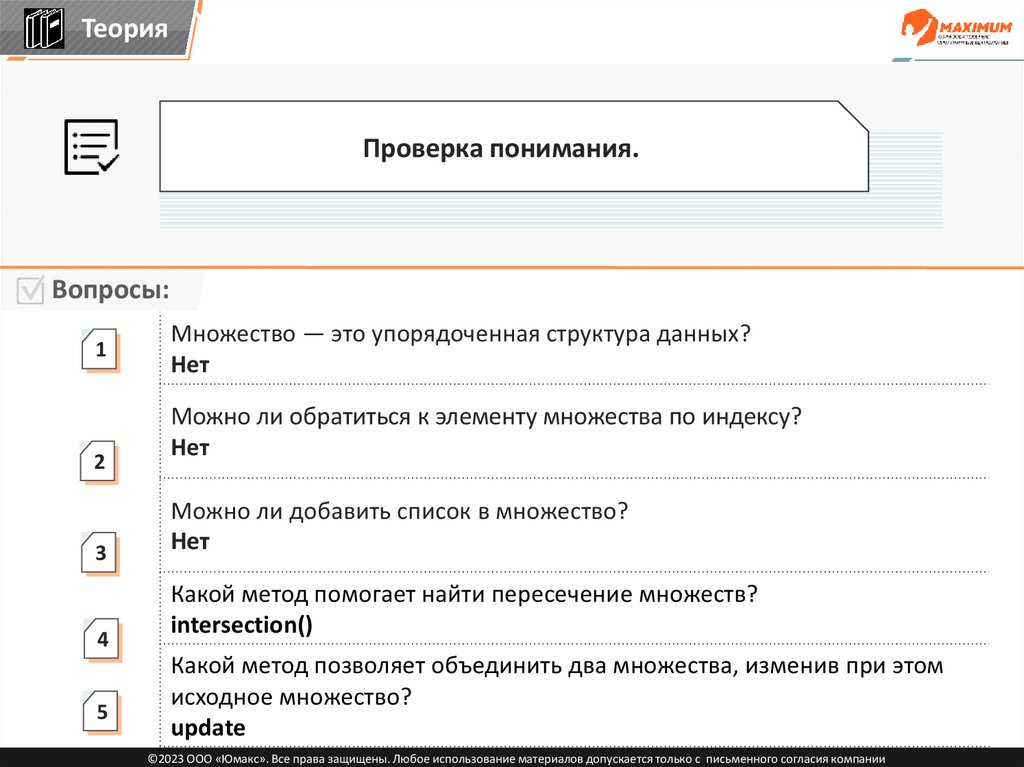
Теория2
Проверка понимания.
Вопросы:
1
2
3
4
5
Множество — это упорядоченная структура данных?
Нет
Можно ли обратиться к элементу множества по индексу?
Нет
Можно ли добавить список в множество?
Нет
Какой метод помогает найти пересечение множеств?
intersection()
Какой метод позволяет объединить два множества, изменив при этом
исходное множество?
update
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
136.
ТеорияDS
Программирование
Python
Спасибо за внимание!
©2023 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании




















































 programming
programming








