Similar presentations:
Стереометрия № 14 (2015 год)
1. Стереометрия № 14 (2015 год)
2. Задача № 4. (Стереометрия, 2015 год)
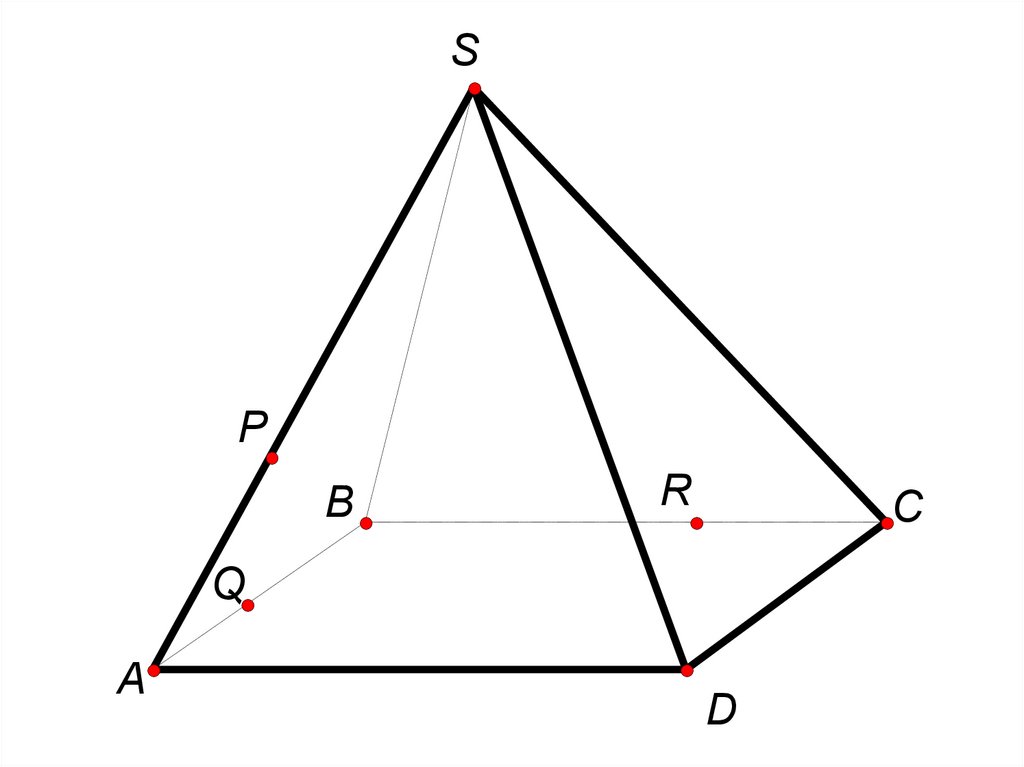
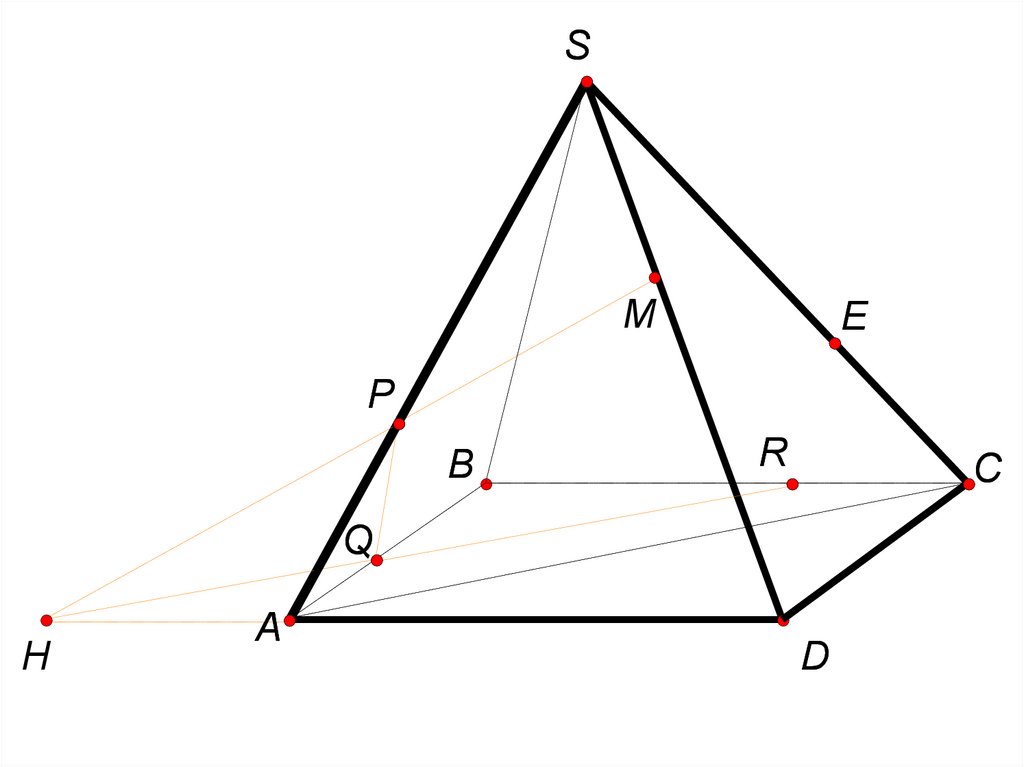
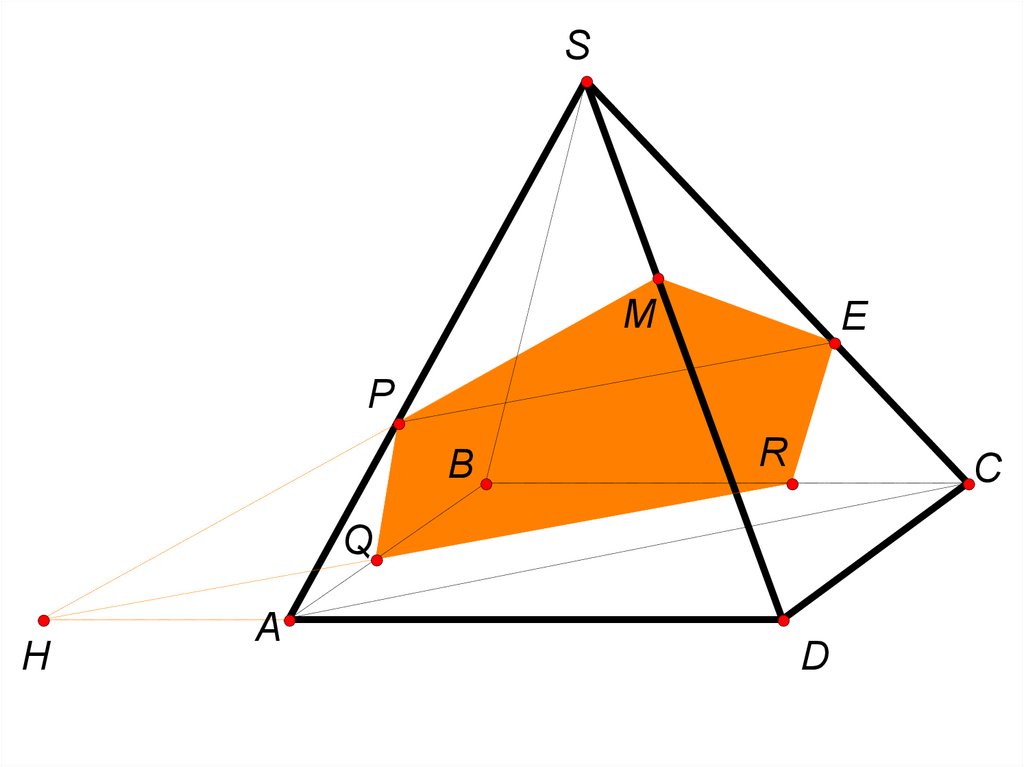
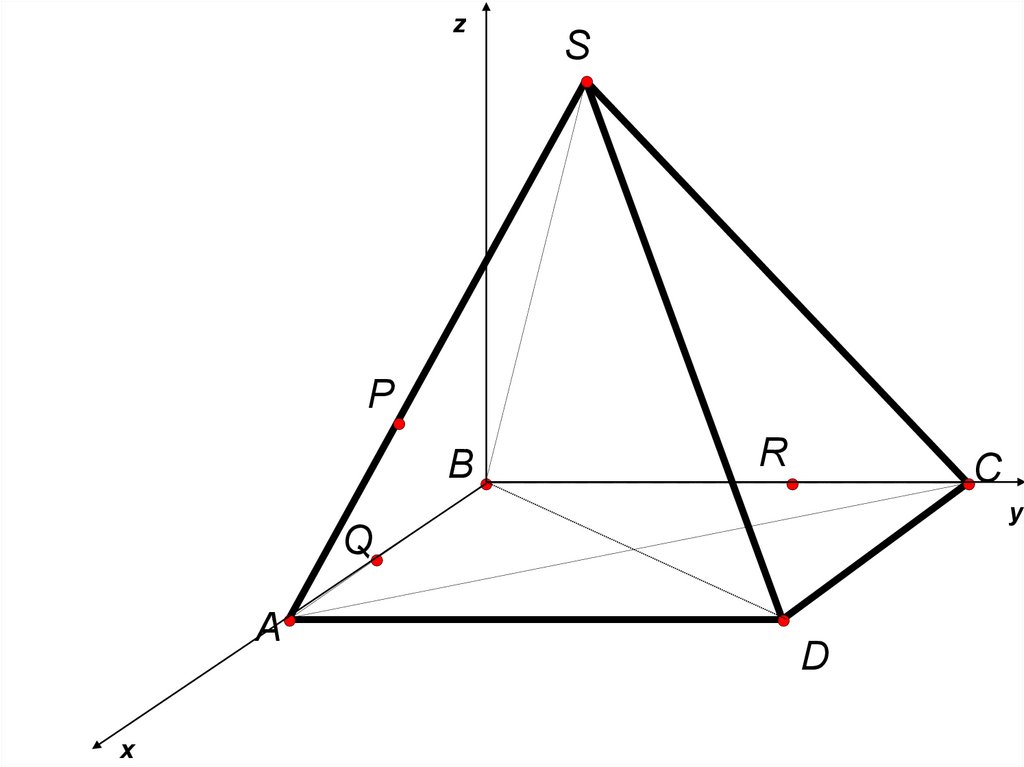
В правильной четырёхугольной пирамидеSABCD все рёбра равны 5. На рёбрах SA,
AB, BC взяты точки P, Q, R соответственно
так, что PA = AQ = RC = 2.
а) Доказать, что плоскость PQR
перпендикулярна ребру SD.
б) Найти расстояние от вершины D до
плоскости PQR.
3.
SP
B
R
C
Q
A
D
4.
SM
E
P
B
R
C
Q
H
A
D
5.
SM
E
P
B
R
C
Q
H
A
D
6.
zS
P
B
R
C
y
Q
A
x
D
7.
8.
9.
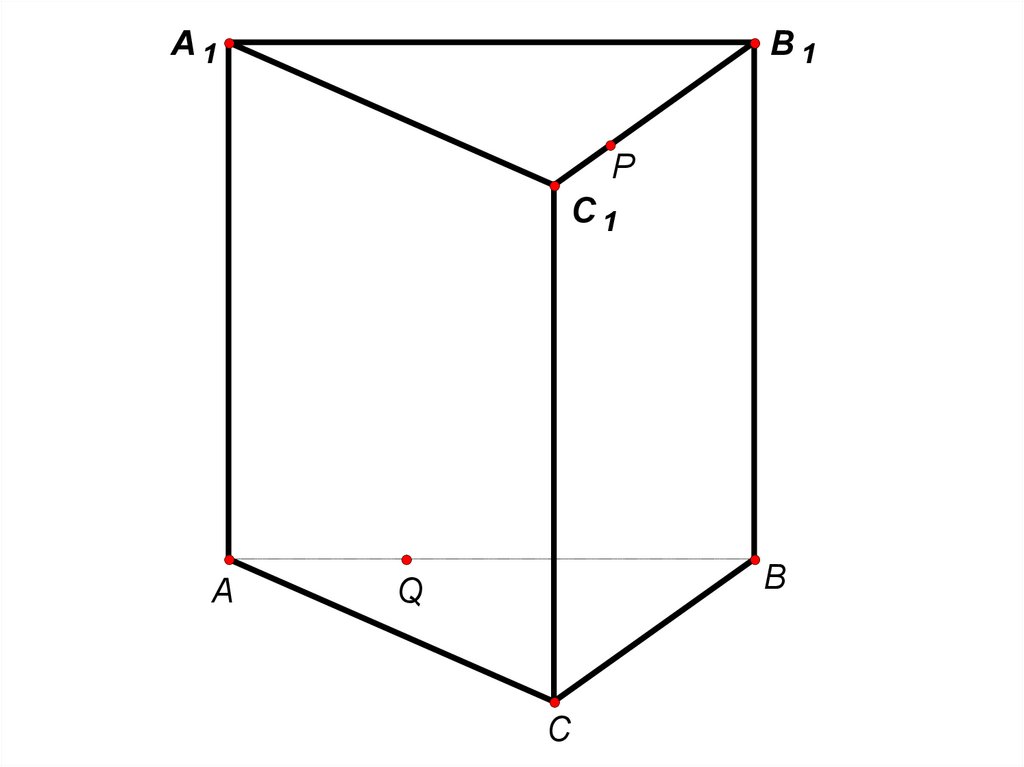
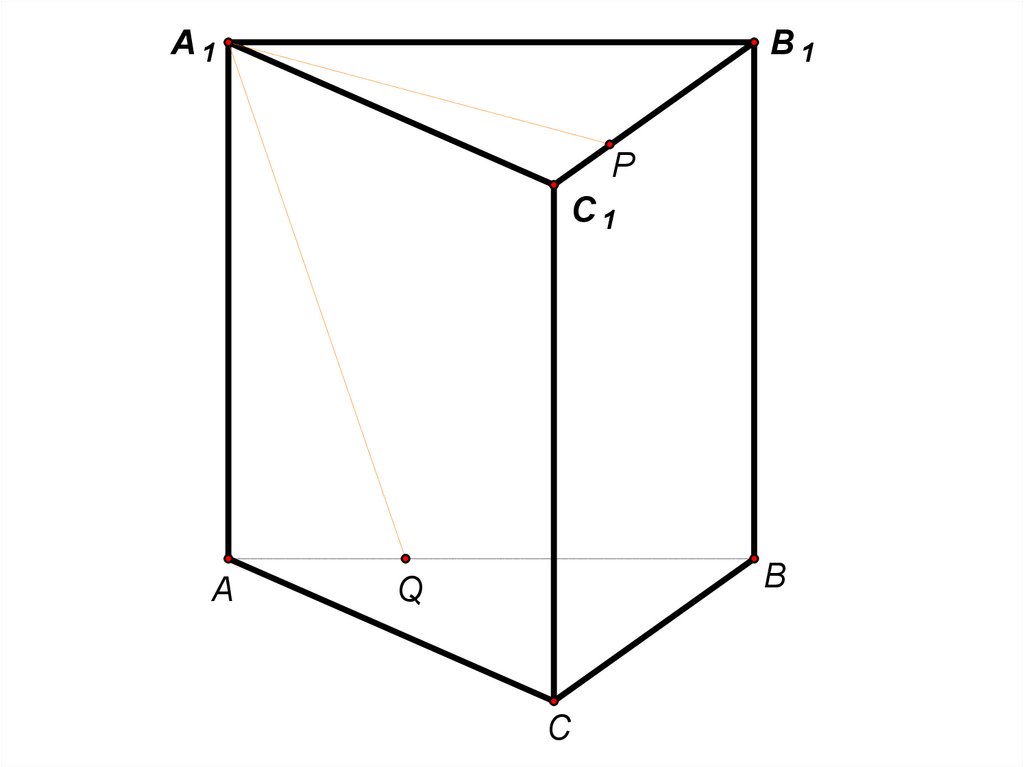
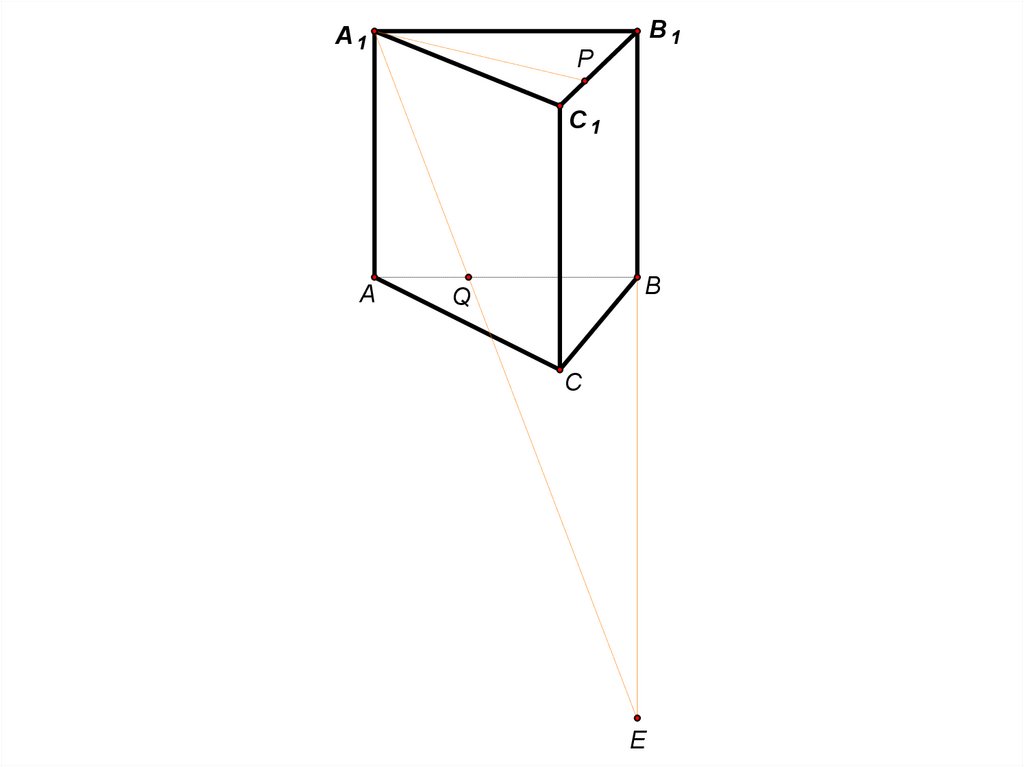
10. Задача 8 (стереометрия, 2015 год)
В правильной треугольной призме ABCA1 B1C1сторона AB основания равна 12, а высота
призмы равна 2. На рёбрах B1C1 и AB отмечены точки
P и Q соответственно, причём PC1 3, а AQ 4.
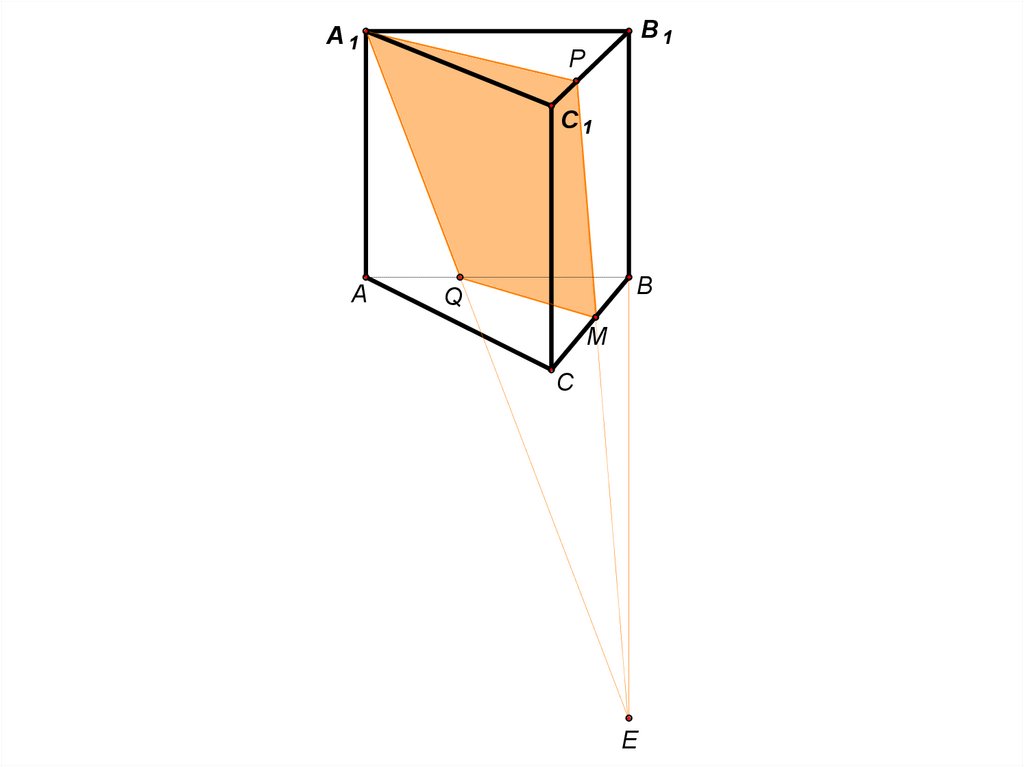
Плоскость A1 PQ пересекает ребро BC в точке M .
а) Доказать, что точка M является серединой ребра BC .
б ) Найти расстояние от точки B до плоскости A1 PQ.
11.
A1B1
P
C1
A
B
Q
C
12.
A1B1
P
C1
A
B
Q
C
13.
B1A1
P
C1
A
B
Q
C
E
14.
B1A1
P
C1
A
B
Q
M
C
E
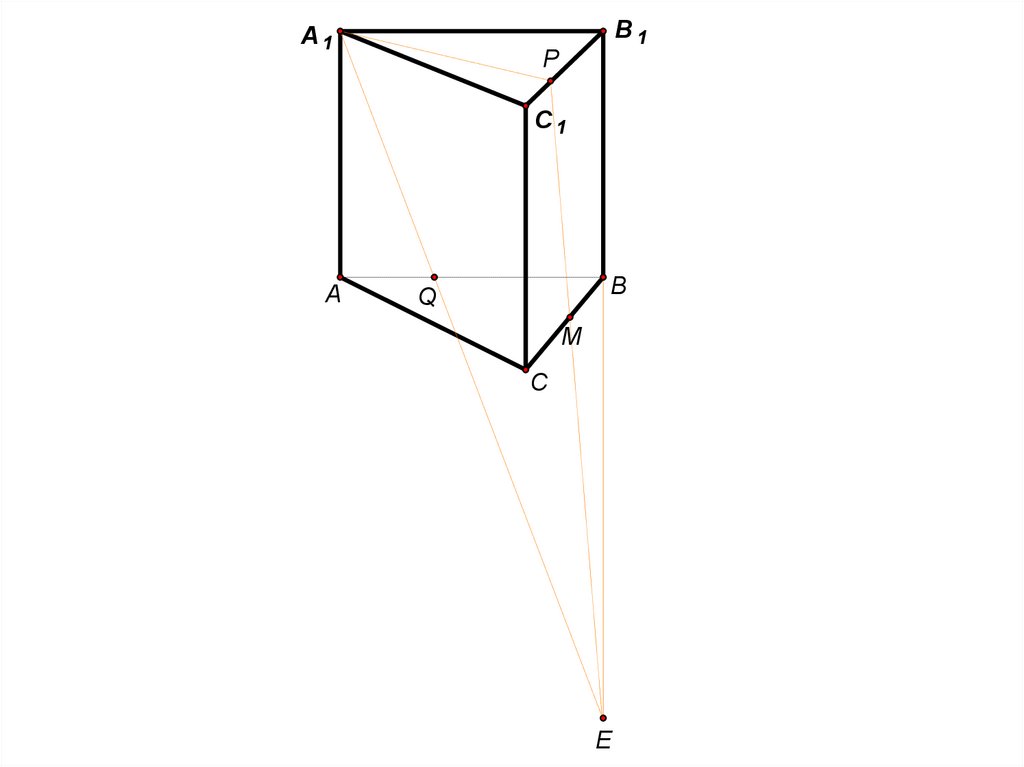
15.
B1A1
P
C1
A
B
Q
M
C
E
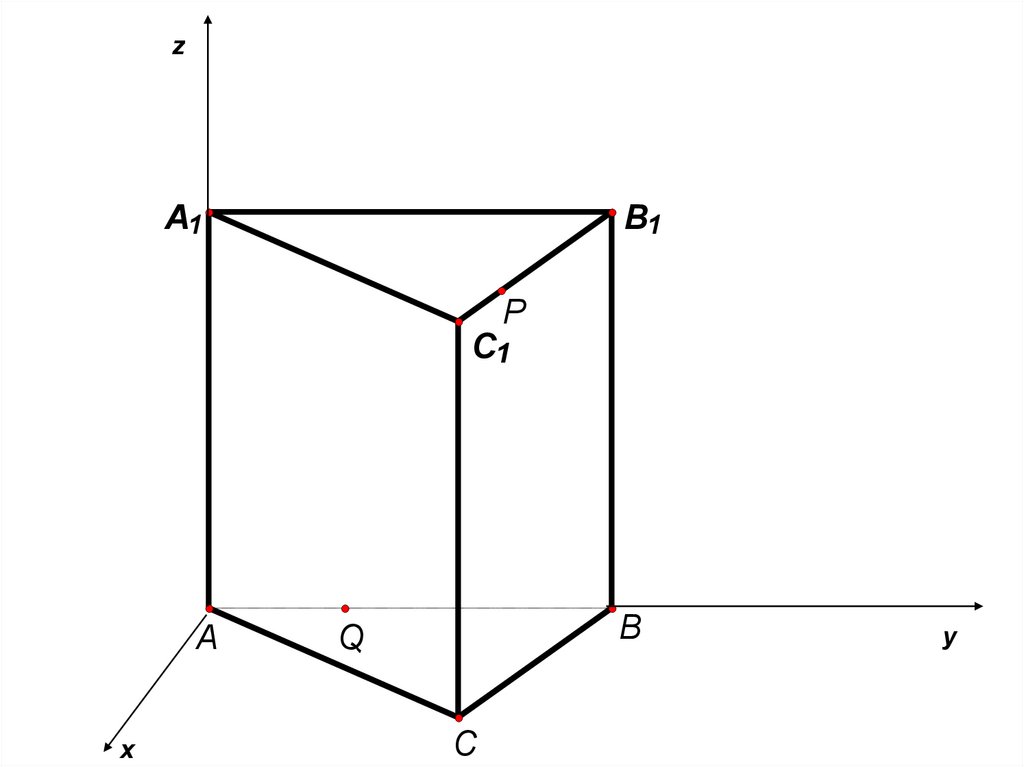
16.
zA1
B1
P
C1
A
x
B
Q
C
y
17.
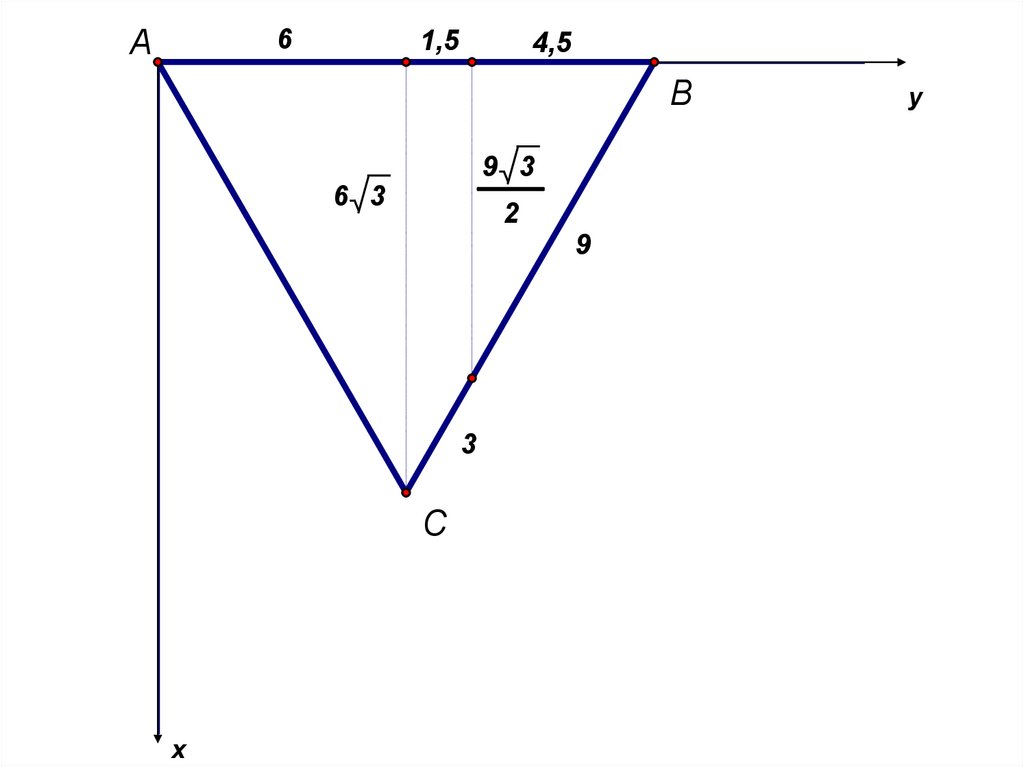
6A
1,5
4,5
B
9 3
6 3
2
9
3
C
x
y






 mathematics
mathematics








