Similar presentations:
Арифметика в эллиптической группе точек по простому модулю. Алгоритм Диффи-Хеллмана на эллиптической кривой
1.
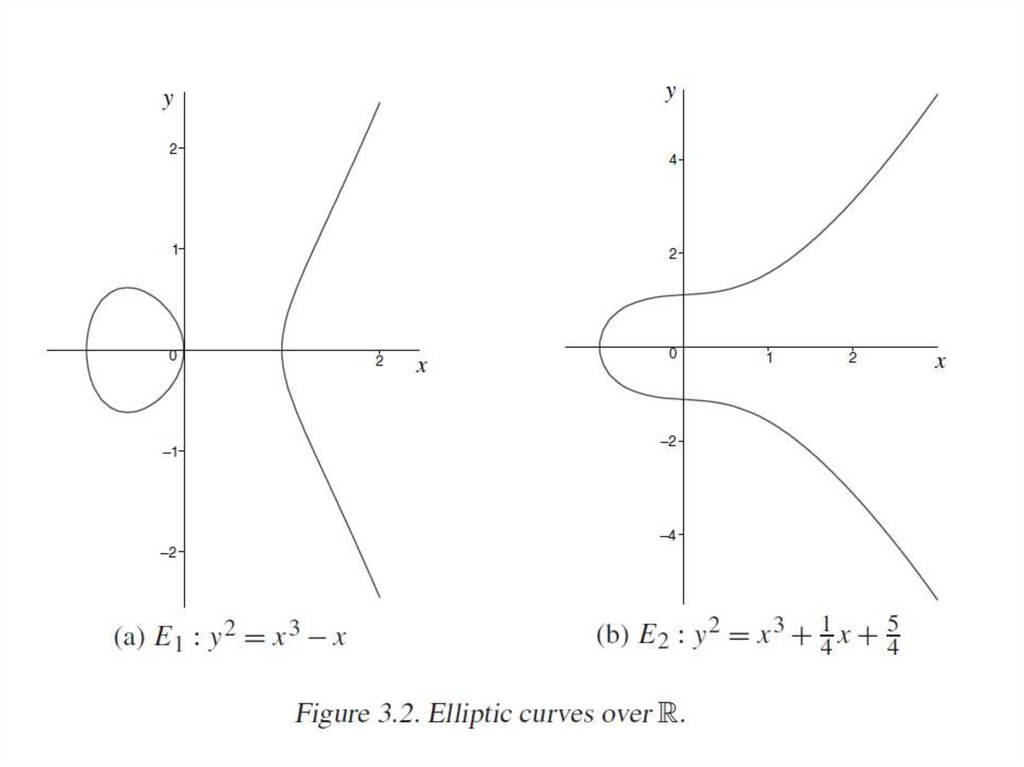
Эллиптические кривые описываются уравнениемy 2 axy by x 3 cx 2 dx e
2.
3. Сложение
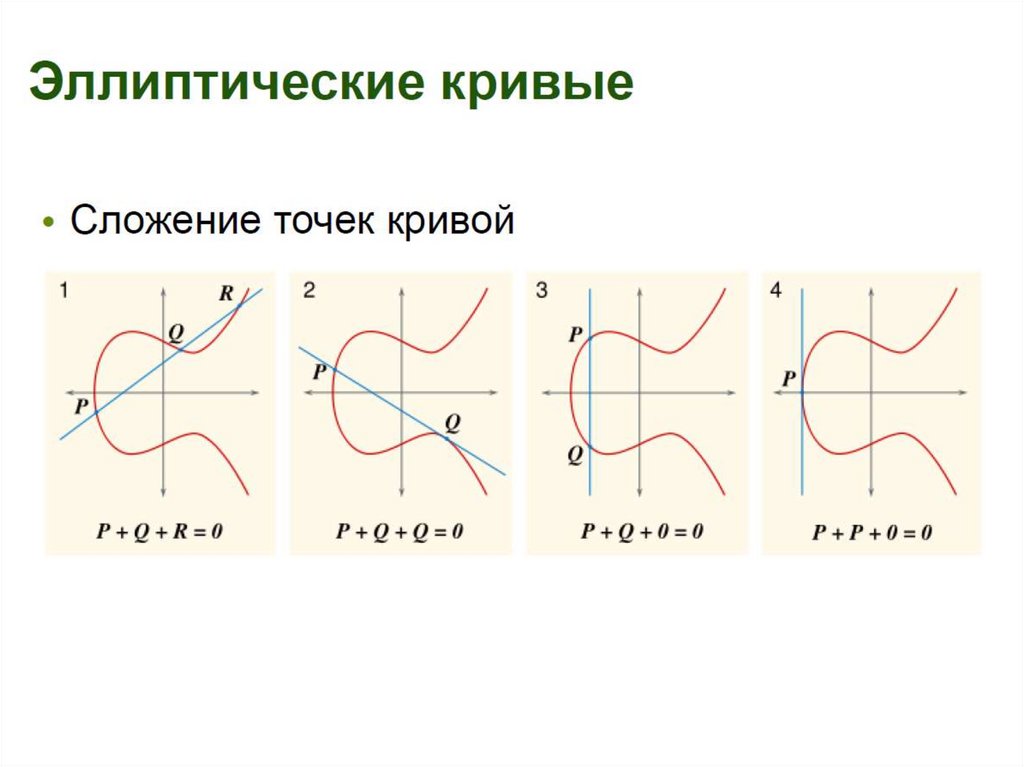
1. Сложение с нулевым элементом ( несобственной точкой O)A A O A
2. Противоположные точки A x; y , A x; y
A-A=O
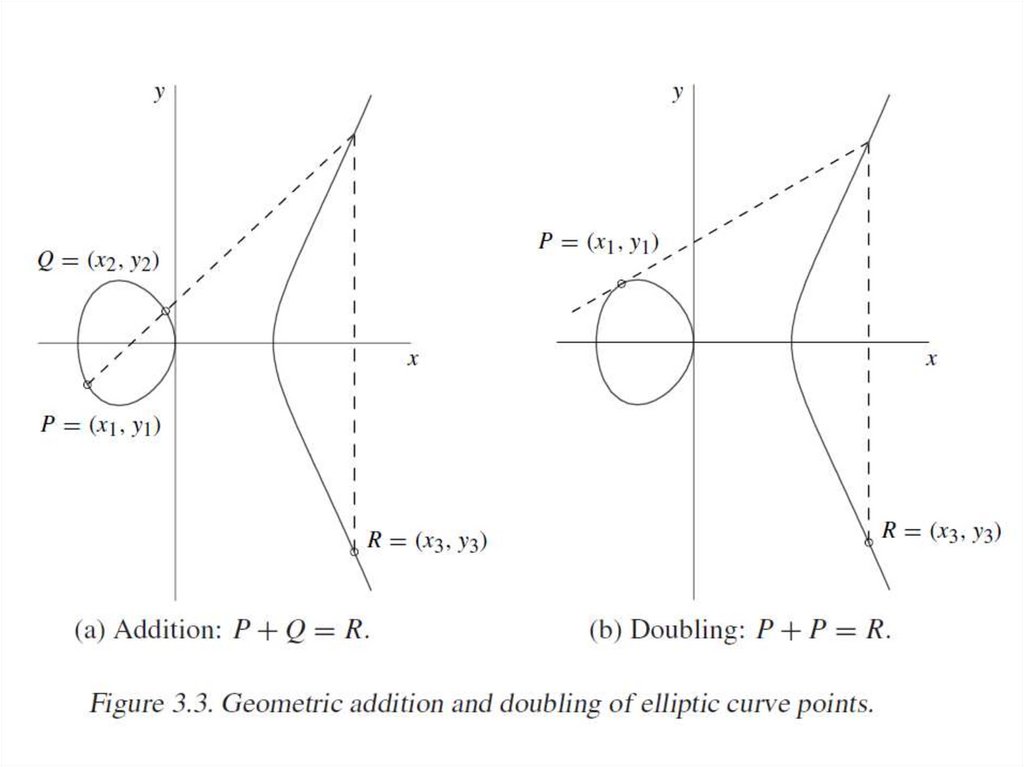
3. Если точки P и Q не удовлетворяют условиям 1 и 2, то прямая, проведенная через эти
две точки имеет еще ровно одну точку пересечения с эллиптической кривой. Эта
точка называется суммой точек P и Q. В вырожденном случае, когда прямая,
проведенная через две точки P и Q , является касательной к одной из этих точек
(например Q), то суммой точек P и Q является точка -Q.
4. Сложение точки самой с собой Q+Q. Проводится касательная к точке Q, ищется
точка пересечения касательной с эллиптической кривой S и в качастве суммы
берется точка, противоположная к S:
Q+Q=2Q= - S
4.
5.
6.
коммутативный и ассоциативный законыk P P P ...P
7.
Эллиптическая группа по модулю p.Эллиптическая группа по модулю p E p a, b
для простого числа p и натуральных чисел a и b
(должно выполняться условие 4a 3 27b 2 mod p 0 )
– множество, элементами которого являются
1) несобственная точка O
2) точки x; y ,
3) координаты которых удовлетворяют следующим условиям:
0 x p 1
0 y p 1
( y 2 ) mod p ( x 3 ax b) mod p
8.
9.
Y6
5
4
3
2
1
0
0
1
2
3
X
4
5
6
10.
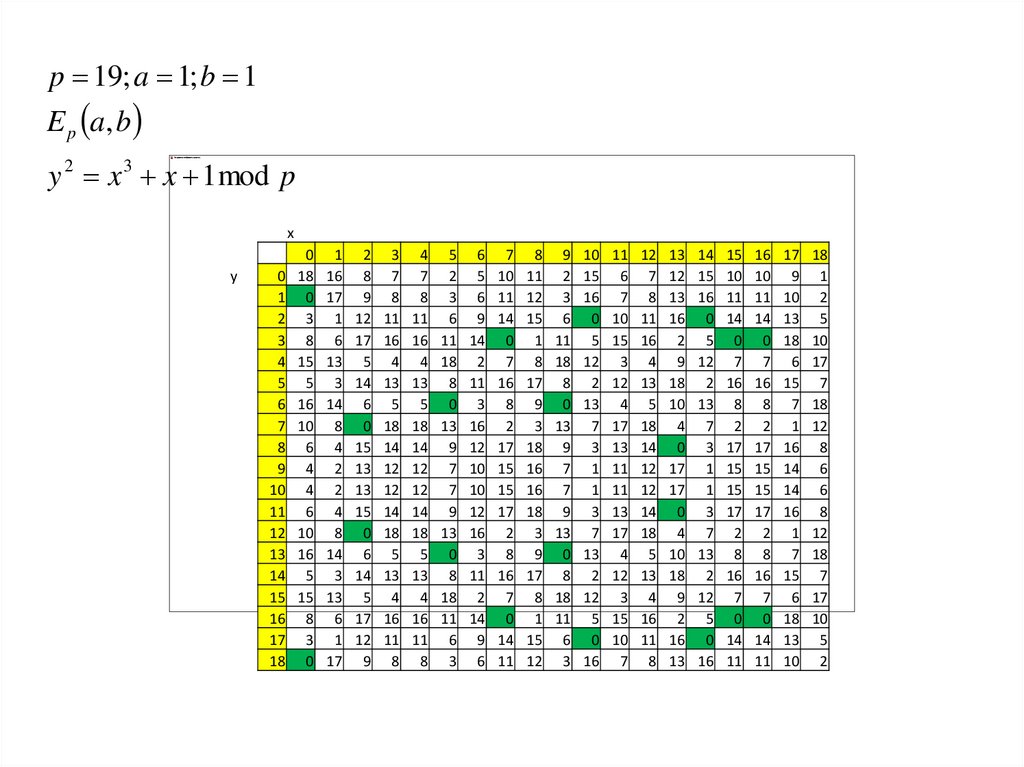
p 19; a 1; b 1E p a, b
y 2 x 3 x 1 mod p
x
y
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
0
18
0
3
8
15
5
16
10
6
4
4
6
10
16
5
15
8
3
0
1
16
17
1
6
13
3
14
8
4
2
2
4
8
14
3
13
6
1
17
2
8
9
12
17
5
14
6
0
15
13
13
15
0
6
14
5
17
12
9
3
7
8
11
16
4
13
5
18
14
12
12
14
18
5
13
4
16
11
8
4
7
8
11
16
4
13
5
18
14
12
12
14
18
5
13
4
16
11
8
5
2
3
6
11
18
8
0
13
9
7
7
9
13
0
8
18
11
6
3
6
5
6
9
14
2
11
3
16
12
10
10
12
16
3
11
2
14
9
6
7
10
11
14
0
7
16
8
2
17
15
15
17
2
8
16
7
0
14
11
8
11
12
15
1
8
17
9
3
18
16
16
18
3
9
17
8
1
15
12
9
2
3
6
11
18
8
0
13
9
7
7
9
13
0
8
18
11
6
3
10
15
16
0
5
12
2
13
7
3
1
1
3
7
13
2
12
5
0
16
11
6
7
10
15
3
12
4
17
13
11
11
13
17
4
12
3
15
10
7
12
7
8
11
16
4
13
5
18
14
12
12
14
18
5
13
4
16
11
8
13
12
13
16
2
9
18
10
4
0
17
17
0
4
10
18
9
2
16
13
14
15
16
0
5
12
2
13
7
3
1
1
3
7
13
2
12
5
0
16
15
10
11
14
0
7
16
8
2
17
15
15
17
2
8
16
7
0
14
11
16
10
11
14
0
7
16
8
2
17
15
15
17
2
8
16
7
0
14
11
17
9
10
13
18
6
15
7
1
16
14
14
16
1
7
15
6
18
13
10
18
1
2
5
10
17
7
18
12
8
6
6
8
12
18
7
17
10
5
2
11.
E 23 1,1 .В этом случае
p 23
a 1
b 1
(4a 3 27b 2 ) mod p 31 mod 23 8 0
Координата x - 0,1,2 …,22.
Для каждого из этих значений x вычисляется
3
( x 1 x 1) mod 23
12.
E 23 1,1 состоит из следующих точек:O;
0,1 ; 0,22 ; 1,7 ; 1,16 ; 3,10 ; 3,13 ; 4,0 ; 5,4 ; 5,19 ; 6,4 ; 6,19 ; 7,11 ; 7,12 ; 9,7 ; 9,16 ; 11,3 ; 1
12,4 ; 12,19 ; 13,7 ; 13,16 ; 17,3 ; 17,20 ; 18,3 ; 18,20 ; 19,5 ; 19,18
13.
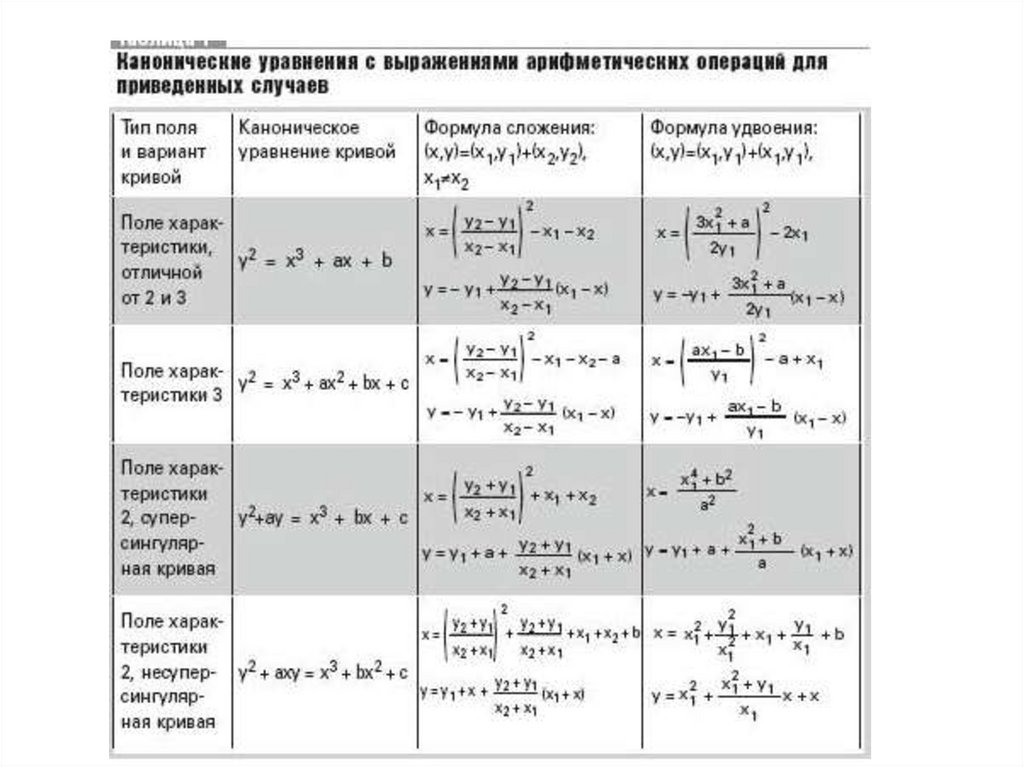
Правила сложения точек в E p a, b :1. P E p a, b P O P
2. P P O; P x; y ; P x; y
3.В остальных случаях сложение точек P x1 ; y1 и Q x2 ; y2 определяется
следующим образом:
P Q x3 ; y 3
x3 2 x1 x 2 mod p
y 3 x1 x3 y1 mod p
y 2 y1
x x mod p, если P Q
2
1
2
3x 1 a mod p, если P Q
2 y1
14.
Пример 1P 3;10 ; Q 9;7
7 10
3
1
P Q
mod 23
mod 23 mod 23 11
9 3
6
2
x3 112 3 9 mod 23 109 mod 23 17
y3 11 3 6 10 mod 23 89 mod 23 20
P Q 17;20
15.
Пример 2P 3;10
2P ?
3 32 1
5
1
mod 23
mod 23 mod 23 6
2 10
20
4
x3 6 2 3 9 mod 23 30 mod 23 7
y 3 6 3 7 10 mod 23 34 mod 23 12
2 P 7;12
16.
Пример заданияЗадана эллиптическая кривая с параметрами p,a,b. Выбрана точка P c
координатами x,y. Пользователи A и B договорились об использовании
алгоритма Диффи-Хеллмана на эллиптической кривой и выбрали
секретные ключи nA и nB.
1 Перечислить все точки указанной эллиптической кривой.
2 Найти открытые ключи пользователей
3 Найти общий ключ
17.
p= 79 a= 1 b= 1K= 0 {x,y}={ O }
K= 1 {x,y}={11, 0}
K= 2 {x,y}={ 0, 1}
K= 3 {x,y}={36, 2}
K= 4 {x,y}={25, 3}
K= 5 {x,y}={32, 4}
K= 6 {x,y}={53, 4}
K= 7 {x,y}={73, 4}
K= 8 {x,y}={23, 5}
K= 9 {x,y}={68, 9}
K= 10 {x,y}={20,11}
K= 11 {x,y}={ 6,12}
K= 12 {x,y}={26,12}
K= 13 {x,y}={47,12}
K= 14 {x,y}={ 2,13}
K= 15 {x,y}={44,15}
K= 16 {x,y}={28,16}
K= 17 {x,y}={ 5,17}
K= 18 {x,y}={37,17}
K= 19 {x,y}={29,18}
K= 20 {x,y}={64,18}
K= 21 {x,y}={65,18}
K= 22 {x,y}={16,20}
K= 23 {x,y}={18,20}
K= 24 {x,y}={45,20}
K= 25 {x,y}={72,21}
K= 26 {x,y}={46,23}
K= 27 {x,y}={54,25}
K= 28 {x,y}={69,27}
K= 29 {x,y}={14,28}
K= 30 {x,y}={15,28}
K= 31 {x,y}={50,28}
K= 32 {x,y}={40,29}
K= 33 {x,y}={ 3,30}
K= 34 {x,y}={30,31}
K= 35 {x,y}={34,32}
K= 36 {x,y}={61,32}
K= 37 {x,y}={63,32}
K= 38 {x,y}={51,33}
K= 39 {x,y}={76,34}
K= 40 {x,y}={21,35}
K= 41 {x,y}={27,35}
K= 42 {x,y}={31,35}
K= 43 {x,y}={33,37}
K= 44 {x,y}={33,42}
K= 45 {x,y}={21,44}
K= 46 {x,y}={27,44}
K= 47 {x,y}={31,44}
K= 48 {x,y}={76,45}
K= 49 {x,y}={51,46}
K= 50 {x,y}={34,47}
K= 51 {x,y}={61,47}
K= 52 {x,y}={63,47}
K= 53 {x,y}={30,48}
K= 54 {x,y}={ 3,49}
K= 55 {x,y}={40,50}
K= 56 {x,y}={14,51}
K= 57 {x,y}={15,51}
K= 58 {x,y}={50,51}
K= 59 {x,y}={69,52}
K= 60 {x,y}={54,54}
K= 61 {x,y}={46,56}
K= 62 {x,y}={72,58}
K= 63 {x,y}={16,59}
K= 64 {x,y}={18,59}
K= 65 {x,y}={45,59}
K= 66 {x,y}={29,61}
K= 67 {x,y}={64,61}
K= 68 {x,y}={65,61}
K= 69 {x,y}={ 5,62}
K= 70 {x,y}={37,62}
K= 71 {x,y}={28,63}
K= 72 {x,y}={44,64}
K= 73 {x,y}={ 2,66}
K= 74 {x,y}={ 6,67}
K= 75 {x,y}={26,67}
K= 76 {x,y}={47,67}
K= 77 {x,y}={20,68}
K= 78 {x,y}={68,70}
K= 79 {x,y}={23,74}
K= 80 {x,y}={32,75}
K= 81 {x,y}={53,75}
K= 82 {x,y}={73,75}
K= 83 {x,y}={25,76}
K= 84 {x,y}={36,77}
K= 85 {x,y}={ 0,78}
18.
2. Сложить точки эллиптическойгруппы точек { 0, 1} и { 32, 4}.
Ответ: { 0, 1}+{ 32, 4}= { 44, 64}.
19.
2. Сложить точки эллиптическойгруппы точек { 0, 1} и { 32, 4}.
Ответ: { 0, 1}+{ 32, 4}= { 44, 64}.
20.
2. Сложить точки эллиптическойгруппы точек { 0, 1} и { 32, 4}.
Ответ: { 0, 1}+{ 32, 4}= { 44, 64}.
x
a
b
q
r
y
1
0
0
1
32
79
0
32
1
0
79
32
2
15
-2
1
32
15
2
2
5
-2
15
2
7
1
-37
15
-37 =
42
21.
2. Сложить точки эллиптическойгруппы точек { 0, 1} и { 32, 4}.
Ответ: { 0, 1}+{ 32, 4}= { 44, 64}.
x
a
b
q
r
1
0
0
1
32
79
0
32
1
0
79
32
2
15
-2
1
32
15
2
2
5
-2
15
2
7
1
-37
15
-37 =
(4 1) * 42 mod 79 47
y
42
22.
2. Сложить точки эллиптическойгруппы точек { 0, 1} и { 32, 4}.
Ответ: { 0, 1}+{ 32, 4}= { 44, 64}.
x
a
b
q
r
y
1
0
0
1
32
79
0
32
1
0
79
32
2
15
-2
1
32
15
2
2
5
-2
15
2
7
1
-37
15
-37 =
(4 1) * 42 mod 79 47
x3 47 2 0 32 mod 79 44
42
23.
2. Сложить точки эллиптическойгруппы точек { 0, 1} и { 32, 4}.
Ответ: { 0, 1}+{ 32, 4}= { 44, 64}.
x
a
b
q
r
y
1
0
0
1
32
79
0
32
1
0
79
32
2
15
-2
1
32
15
2
2
5
-2
15
2
7
1
-37
15
(4 1) * 42 mod 79 47
x3 47 2 0 32 mod 79 44
y3 47(0 44) 1) mod 79 64
-37 =
42
24.
3. 2. Сложить точки эллиптическойгруппы точек { 32, 4} и { 32, 4}.
Ответ { 32, 4}+{ 32, 4}= { 16, 59}.
25.
5. Найти точку 20 { 20, 11}.Ответ
20 { 20, 11} = { 23, 74}.
Решение
2010 10100
20{20,11} 16{20,11} 4{20,11}.
2{20,11} {64,18}
4{20,11} 2{64,18} {21,35}
8{20,11} 4{64,18} 2{21,35} {32,75}
16{20,11} 8{64,18} 4{21,35} 2{32,75} {26,67}
20{20,11} 16{20,11} 4{20,11} {21,35} {26,67} {23,74}
26.
27.
28.
29.
30.
Q kP .1. Выбираем простое число p и параметры a и b для эллиптической группы точек
E p a, b .
2. Выбираем генерирующую точку G x1 ; y1 . При выборе G важно, чтобы nG=0
при достаточно большом значении n.
Параметры E p a, b и G известны всем участникам. Обмен ключами между
абонентами A и B происходит следующим образом.
1. A выбирает целое число n A , меньшее n ( Это личный ключ A).
A вычисляет PA n AG . Эта точка из E p a, b - публичный ключ A
B выбирает целое число n B , меньшее n ( Это личный ключ B).
B вычисляет PB nB G . Эта точка из E p a, b - публичный ключ B
2. A и B обмениваются своими публичными ключами по открытому каналу
связи.
3. A вычисляет общий ключ – точку из E p a, b : K n A PB
B вычисляет общий ключ : K nB PA
31.
Алгоритм Диффи-ХеллманаПользователи A и B договорились использовать эллиптическую
кривую
p= 79 a= 1 b= 1
и точку P={11,0}.
Пользователь A сгенерировал приватный ключ nA=5.
Пользователь B сгенерировал приватный ключ nB=8.
Провести вычисление общего ключа с точки зрения A и с точки
зрения B.
Решение
y A 5{11,0} {32,4}
y B 8{11,0} {23,5}
K A 5{23,5} {21,35}
K B 8{32,4} {21,35}









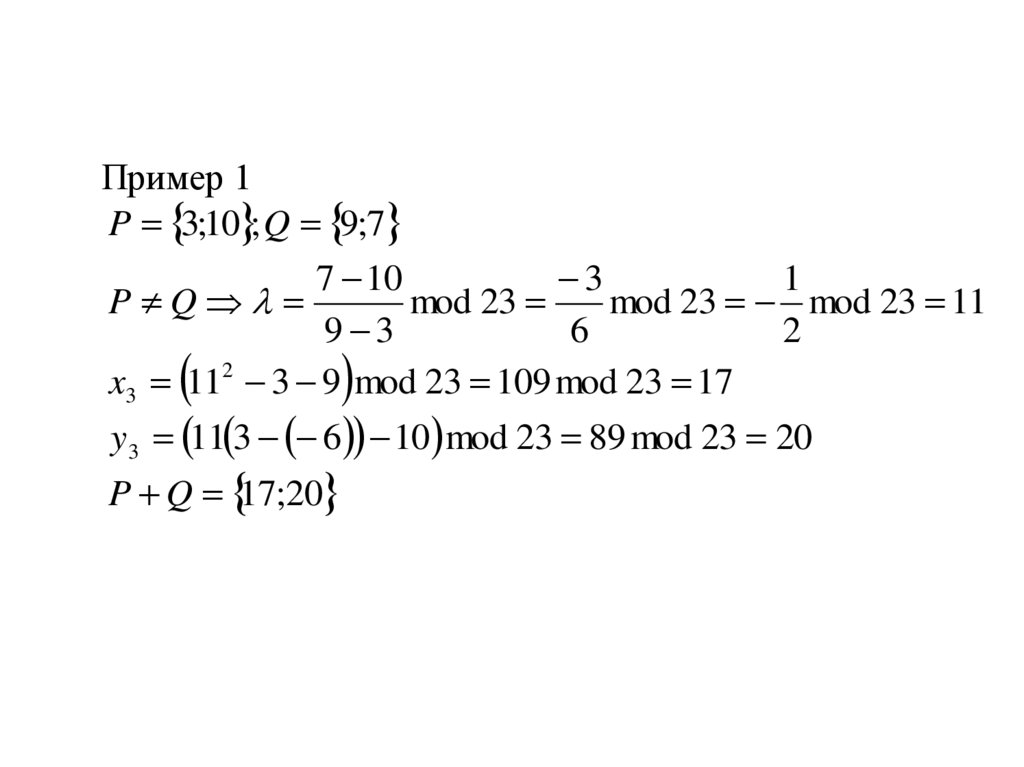
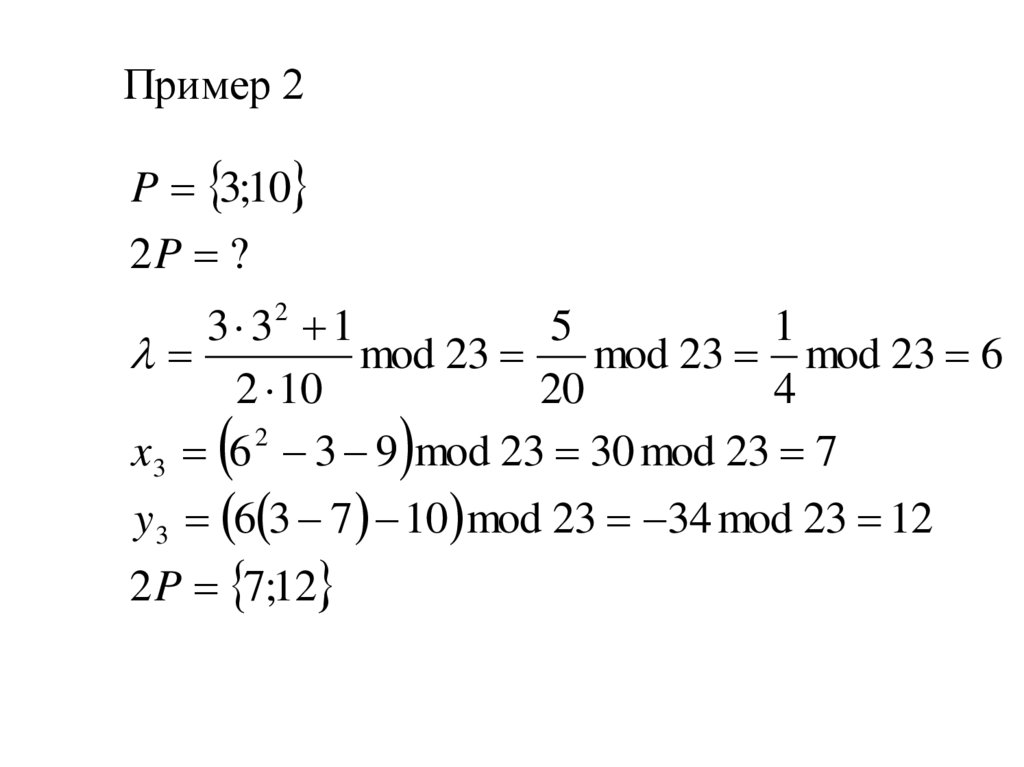


























 mathematics
mathematics








