Similar presentations:
Нелинейные электрические цепи
1. МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ ИРКУТСКИЙ ФИЛИАЛ КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТГРАЖДАНСКОЙ АВИАЦИИ
ИРКУТСКИЙ ФИЛИАЛ
КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И ПИЛОТАЖНОНАВИГАЦИОННЫХ КОМПЛЕКСОВ
ЛЕКЦИЯ № 5
по дисциплине
Электротехника
ТЕМА № 5
Нелинейные электрические цепи
2. Вопросы лекции
5.1. Основные свойства и особенности нелинейныхэлектрических цепей постоянного и переменного тока.
5.2. Методы расчета нелинейных цепей. Статическое и
дифференциальное сопротивление. Расчет цепи при
последовательном соединении элементов. Расчет цепи
при параллельном соединении элементов.
3. 5.1. Основные свойства и особенности нелинейных электрических цепей постоянного и переменного тока.
Нелинейной электрической цепью называют такую, в которой имеется хотябы один нелинейный элемент (НЭ).
В качестве НЭ в электрической цепи могут быть: нелинейные резистор,
катушка и конденсатор, которые на схемах обозначаются соответственно:
(рис.5.1.1).
Рис.5.1.1
Нелинейным элементом (НЭ) называют элемент, электрическое
сопротивление, индуктивность или емкость которого зависит от режима цепи,
т.е. от величины или направлений токов или напряжений на этих элементах.
Для нелинейных цепей и их элементов R const , L const , C const .
Нелинейные элементы находят широкое применение в авиационном
оборудовании ЛА: в системах электроснабжения, в электрических машинах, в
автоматике, в бортовых вычислительных машинах, в электронных устройствах,
измерительной технике, радиолокаций и др.
4.
Свойства нелинейных цепей определяются свойствами нелинейныхэлементов, включенных в эти цепи.
Рассмотрим основные свойства (НЭ).
Для количественного описания свойств НЭ используются специальные
зависимости, называемые характеристиками: вольт-амперные (ВАХ) U I
(резистор), вебер-амперные i - (катушка индуктивности), кулон-вольтные
q u (конденсатор), которые являются нелинейными. И с этих позиций можно
дать другое определение для нелинейных элементов:
Нелинейным элементом НЭ называют такой элемент ЭЦ, который имеет
нелинейную характеристику.
Обычно характеристики получают экспериментально и представляют в виде
графиков, таблиц или приближенно представляют аналитически.
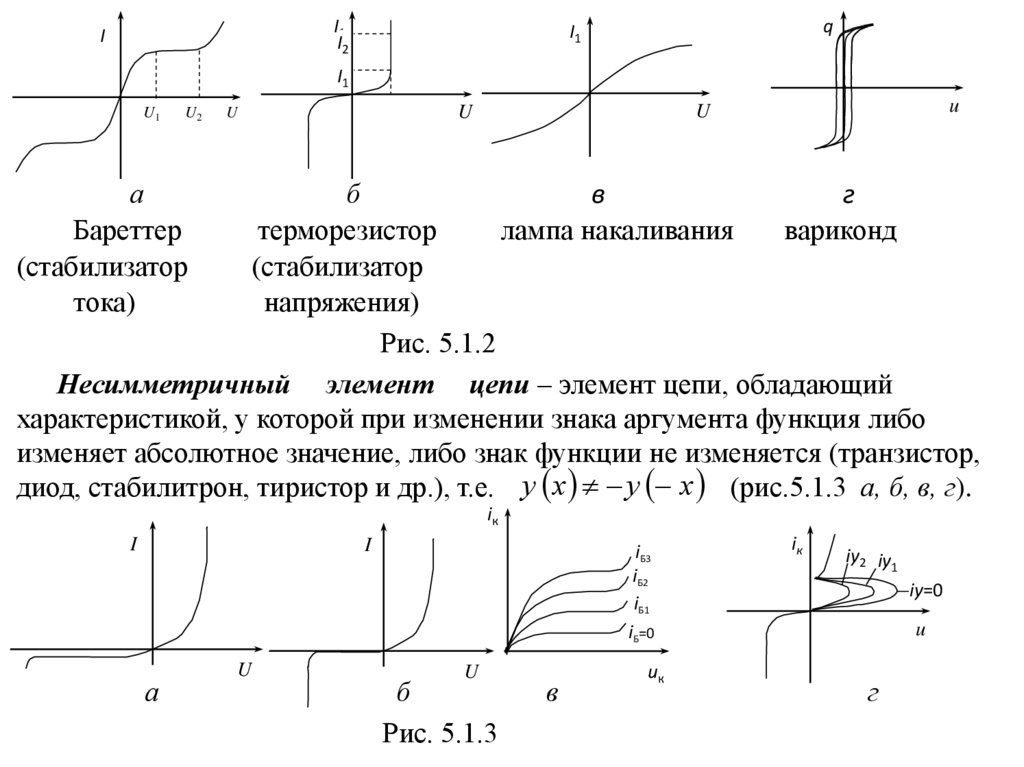
1. По степени симметрии характеристик НЭ относительно осей координат
их можно подразделить на две группы: симметричные и несимметричные
Симметричный элемент цепи – элемент, обладающий характеристикой,
у которой знак функции изменяется при изменении знака аргумента, но
абсолютное значение функции сохраняется, т.е. y x у x . Симметричными
характеристиками обладают бареттер, терморезистор (термистор, если ТКρ 0
позистор, если ТКρ 0 ), лампа накаливания, нелинейный конденсатор
(вариконд). (рис.5.1.2 а, б, в, г). (ТКρ – температурный к-т сопротивления)
5.
I1I2
I
q
I1
I1
U1
U2
u
U
U
U
а
Бареттер
(стабилизатор
тока)
б
в
г
терморезистор
лампа накаливания
вариконд
(стабилизатор
напряжения)
Рис. 5.1.2
Несимметричный элемент цепи – элемент цепи, обладающий
характеристикой, у которой при изменении знака аргумента функция либо
изменяет абсолютное значение, либо знак функции не изменяется (транзистор,
диод, стабилитрон, тиристор и др.), т.е. у x y x (рис.5.1.3 а, б, в, г).
iк
I
I
а
U
iБ3
iБ2
iБ1
iБ=0
U
б
Рис. 5.1.3
в
uк
iк
iy2 iy1
iy=0
u
г
6.
2. Другое свойство нелинейных элементов связано с различием илисовпадением их характеристик для мгновенных и действующих значений
токов и напряжений. Отсюда их деление на инерционные и безинерционные.
Инерционными называют НЭ, которые имеют различные характеристики
для мгновенных и действующих токов и напряжений. У них ВАХ линейные для
мгновенных и нелинейные для действующих (терморезисторы, лампы
накаливания). Нелинейные свойства этих элементов связаны с тепловыми
(инерционными, медленно протекающими) процессами: изменением
температуры окружающей среды или нагревом протекающим током.
Безинерционными называют НЭ, у которых характеристики для мгновенных
и действующих значений токов и напряжений совпадают (диод, транзистор,
тиристор, нелинейный конденсатор, стабилитрон).
3. По режиму работы в электрической цепи НЭ подразделяются на
управляемые и неуправляемые.
Управляемые НЭ кроме основной цепи имеют по крайней мере еще одну
вспомогательную (управляющую) цепь, воздействия на ток или напряжение
которой можно изменять ВАХ основной цепи (транзистор, тиристор, триод и
т.д.) .
Неуправляемые НЭ не имеют управляющих цепей (диод, бареттер,
термистор, лампа накаливания).
В управляемых НЭ ВАХ изображается одной кривой, а в неуправляемых –
семейством кривых.
7.
Особенности:1. В нелинейных цепях постоянного и переменного тока параметры
нелинейных элементов зависят от режима цепи.
2. Для количественной оценки параметров НЭ в электрических
нелинейных цепях применяют понятия статических и дифференциальных
(динамических) сопротивлений, индуктивности и емкости.
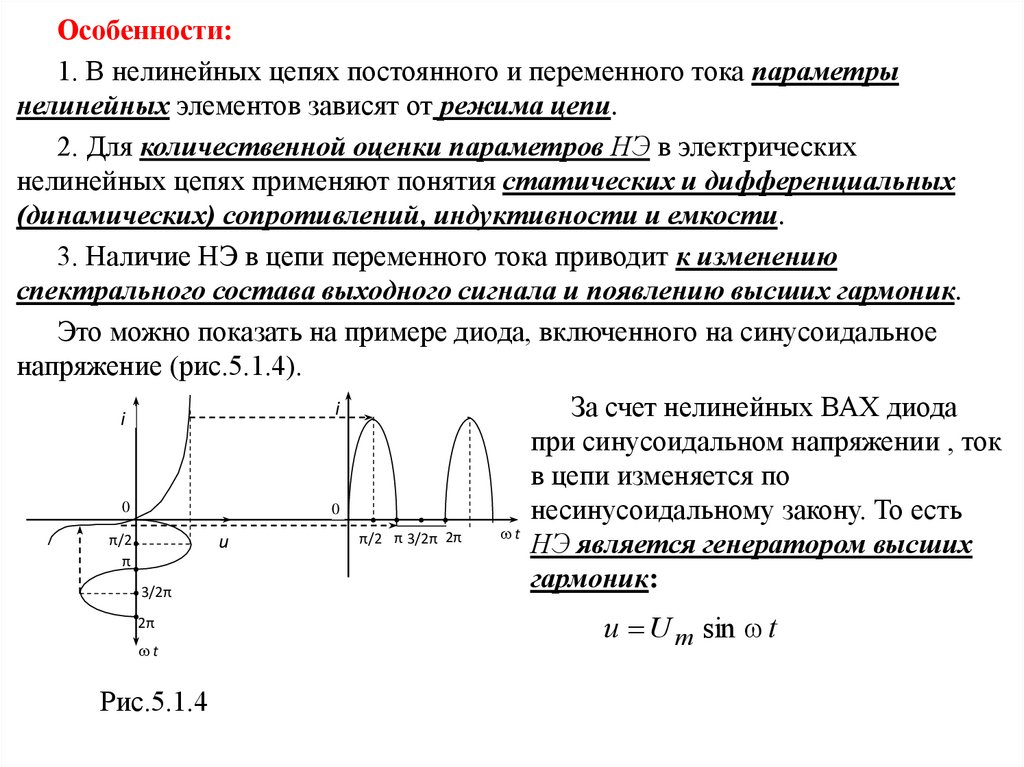
3. Наличие НЭ в цепи переменного тока приводит к изменению
спектрального состава выходного сигнала и появлению высших гармоник.
Это можно показать на примере диода, включенного на синусоидальное
напряжение (рис.5.1.4).
i
За счет нелинейных ВАХ диода
i
при синусоидальном напряжении , ток
в цепи изменяется по
0
0
несинусоидальному закону. То есть
t
π/2 π 3/2π 2π
π/2
u
НЭ является генератором высших
π
гармоник:
3/2π
2π
t
Рис.5.1.4
u U m sin t
8.
Im 12
2
i t
I m cos t
I m cos 2 t
I m cos 4 t
2
3
15
В полученной несинусоидальной кривой тока содержится постоянная
составляющая, когда и 0, обратный ток практически отсутствует. Этот
эффект носит название вентильного действия НЭ и используется при
выпрямлении переменного тока.
4. Появление высших гармоник в большинстве энергоустановок
нежелательно, так как приводит к уменьшению cos (коэффициент а
мощности) и усложнению расчета цепи.
5. При определенных условиях в некоторых нелинейных цепях могут
возникать физические явления, принципиально невозможные в линейных
цепях: автоколебания, автомодуляция, триггерные явления (об этом в
электронике подробнее).
6. Свойства нелинейных элементов лежат в основе принципа действия
некоторых преобразователей, широко используемых в АО:
- преобразование переменного тока в постоянный (схемы выпрямления на
основе диодов в системах электроснабжения ЛА);
- стабилизация тока для питания цепей накала электронных ламп
(бареттеры);
- стабилизация напряжения (термисторы, стабилитроны) в блоках питания
САУ и БЦВМ;
9.
- измерение и регулировка температуры, а так же защита от перегреваавиационных асинхронных двигателей, трансформаторов (терморезисторы,
термисторы);
- преобразование частоты (умножение или деление (нелинейные
конденсаторы-вариконды);
- бесконтактные реле (тиристор);
- усиление мощности (транзисторы) (в электрических машинах, САУ) и т.д.
7. Процессы, происходящие в нелинейных электрических цепях
постоянного и переменного тока описывают нелинейными алгебраическими
или дифференциальными уравнениями, точное решение которых, как правило,
неизвестно. А все методы их решения – специфические и приближенные.
ВЫВОД: Изучив основные свойства и особенности нелинейных цепей
постоянного и переменного тока Вы имеете представление об использовании
этих электрических явлений в электротехнических устройствах –
преобразователях, широко применяемых в АО ЛА.
10. 5.2. Методы расчета нелинейных цепей.
При расчете нелинейных цепей постоянного тока нелинейныеалгебраические уравнения могут быть решены графоаналитическими,
численными и аналитическими методами.
Из них самым простым и довольно точным при выполнении инженерных
расчетов является графоаналитический.
Графоаналитические методы
В цепях постоянного тока широкое распространение получили
графоаналитические методы расчета, в которых ВАХ используется для решения
нелинейных уравнений, составленных на основании законов Кирхгофа.
Статическое и дифференциальное сопротивление
В некоторых случаях возникает необходимость в расчете статического и
дифференциального сопротивлений нелинейного элемента.
Статическим называют сопротивление, которое определяет значение
тока при заданном напряжении.
Оно рассчитывается по формуле:
U mU
,
tgα K tgα
I
mI
т.е. как отношение постоянного напряжения к постоянному току,
протекающему по нелинейному элементу.
Rcm
11.
Статическое сопротивление определяется по углу наклона луча,проведенного из начала координат в рабочую точку характеристик, для которой
определяется сопротивление (рис.5.2.1). Угол образован лучом и осью тока.
Где mU , mI - масштабы напряжения и тока. Очевидно, что статическая
проводимость может быть определена по формулам:
I или
1
Gcm
Gcm ctgα
U
K
Дифференциальное
I
U
сопротивление определяется
как предел отношения
A
приращения напряжения к
U
A
β
β
приращению тока при I,
I
α
стремящемуся к нулю:
α
β
U
U d U U
Rд lim
dI
I
I 0 I
I
Рис. 5.2.1.
Дифференциальное сопротивление показывает, как изменяется ток при
изменении напряжения. Дифференциальное сопротивление пропорционально
тангенсу угла наклона касательной в рабочей точке характеристики:
mU
Rд
tg K tg
mI
где угол образован касательной K рабочей точке ВАХ и осью тока.
12.
Соответственно дифференциальная проводимость равна:1
dI
или
Gд ctg
Gд
K
dU
Статическое и дифференциальное сопротивление изменяются с изменением
положения рабочих точек на характеристике. При этом статическое
сопротивление всегда остается положительной конечной величиной, а
дифференциальное может быть равно нулю (точка А на рис.5.2.2 а, б),
бесконечности и даже становится отрицательным (на падающем участке АВ,
рис.5.2.2 в). Параметр Rд применяется при исследовании режима работы
цепи в случае небольших отклонений тока и напряжения от какого-то значения.
Статическое и дифференциальное сопротивления в общем случае не равны друг
другу. Rcm Rд
, если ВАХ линейна.
U
I
U
A Rд=0
A Rд=0
α
0
0
а
I
б
Рис.5.2.2
U
0
в
β
I
13.
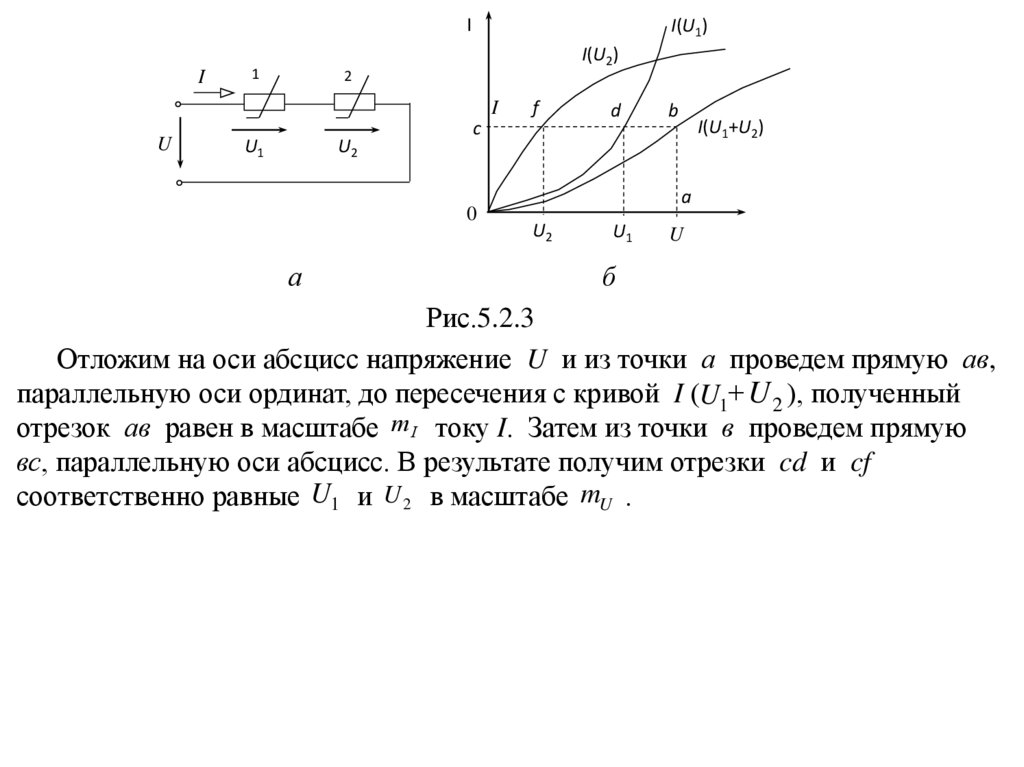
Расчет цепи при последовательном соединении элементовНа рис. 5.2.3 а показано последовательное соединение двух нелинейных
элементов, вольтамперные характеристики которых заданы (рис.5.2.3 б). Пусть
требуется определить ток I и напряжения на элементах при заданном
напряжении на зажимах цепи.
I
I
I(U1)
I(U2)
1
2
I
U
U2
U1
c
0
а
f
d
b
I(U1+U2)
a
U2
U1
U
б
Рис.5.2.3
Для вычисления тока и напряжения U1 и U 2 построим вспомогательную
характеристику: зависимость тока I от суммарного напряжения U1 + U 2 .
Так как I1 I 2 I const , то для построения характеристики I (U1 + U 2 )
необходимо суммировать напряжения U1 и U 2 при одинаковых значениях тока
I (рис.5.2.3 б).
14.
II
I(U1)
I(U2)
1
2
I
U
U2
U1
c
0
а
f
d
b
I(U1+U2)
a
U2
U1
U
б
Рис.5.2.3
Отложим на оси абсцисс напряжение U и из точки а проведем прямую ав,
параллельную оси ординат, до пересечения с кривой I (U1+ U 2 ), полученный
отрезок ав равен в масштабе m I току I. Затем из точки в проведем прямую
вс, параллельную оси абсцисс. В результате получим отрезки cd и cf
соответственно равные U1 и U 2 в масштабе mU .
15.
Расчет цепи при параллельном соединенииНа рис.5.2.4 а показаны параллельно соединенные нелинейные элементы 1
и 2, ВАХ которых заданы (рис.5.2.4 б).
I
(I1+I2)U
I
c
I1(U1)
b
1
2
f
I1
I2
d
I2(U2)
U
0
а
a
U
U
б
Рис.5.2.4
Пусть напряжение на зажимах цепи равно U, тогда по ВАХ I1 U1 и I 2 U 2
легко определить токи I1 и I 2 в нелинейных элементах, а на основании первого
закона Кирхгофа I1 и I 2 I1 = I - ток в неразветвленной части цепи.
Если задан ток I , то для определения напряжения U и токов I1 и I 2 в
нелинейных элементах надо построить вспомогательную характеристику
( I1 + I 2 )(U), т.е. зависимость суммарного тока от напряжения U.
16.
Так как при параллельном соединении U1 U 2 U , то для построения этойхарактеристики в соответствии с уравнением I = I1 + I 2 суммируем ординаты
кривых I1 U и I 2 U для одних и тех же значений напряжения U1 U 2 . Затем
отложим на оси у отрезок, равный в масштабе m I току I , и проведем из
точки С прямую св, параллельную оси абсцисс, до пересечения с
характеристикой ( I1 + I 2 )(U), полученный отрезок св= 0a равен в масштабе mU
напряжению U. Наконец, проводим прямую из точки в, параллельную оси
ординат, до пересечения с осью абсцисс. В результате получим отрезки, а d и a f
равные в масштабе mI токам I1 и I 2 .
Таким же путем можно рассчитать электрическую цепь с любым числом
параллельно включенных нелинейных элементов.
I
(I1+I2)U
I
c
I1(U1)
b
1
2
f
I1
I2
d
I2(U2)
U
0
a
U
U
17.
ВЫВОД:Изучив приближенные графоаналитические методы,
применяемые для решения нелинейных алгебраических уравнений, которые
описывают процессы в нелинейных электрических цепях постоянного тока, в
случаях последовательного и параллельного соединения нелинейных элементов,
Вы знаете и сумеете использовать эти методы анализа и расчета нелинейных
электрических цепей постоянного тока.
Особые, специфические свойства нелинейных элементов позволяют с одной
стороны использовать их для создания различных преобразователей, а с другой
стороны ведут к ухудшению работы энергоустановок и уменьшению их
коэффициента мощности из-за появления высших гармоник.
18. заключение
Таким образом, в результате рассмотрения материала вы получили знания :об основных свойствах и особенностях нелинейных электрических цепей
постоянного и переменного тока;
о методах расчета нелинейных цепей, статическом и дифференциальном
сопротивлении, расчете цепи при последовательном соединении
элементов, расчете цепи при параллельном соединении элементов.















 physics
physics








