Линейные ДУ 1 порядка

1.

Линейные ДУ 1 порядка
Лутковская Е.А.

2.

Линейное ДУ 1 порядка

3.

Метод Бернулли

4.

Пример

5.

Замечание

6.

Способ Лагранжа.
Метод вариации произвольной постоянной.

7.

Способ Лагранжа. Продолжение.

8.

Способ Лагранжа.
Окончание.

9.

Пример.

10.

Жозеф-Луи Лагранж
Жозе́ ф Луи́ Лагра́ нж (фр. Joseph Louis Lagrange, итал.
Giuseppe Lodovico Lagrangia; 25 января 1736, Турин —
10 апреля 1813, Париж) — французский математик,
астроном и механик итальянского происхождения.
Наряду с Эйлером — крупнейший математик XVIII
века. Особенно прославился исключительным
мастерством в области обобщения и синтеза
накопленного научного материала.

11.

Уравнение Бернулли.
или приводить к ЛДУ-1
подстановкой y1-n=z

12.

Пример.

13.

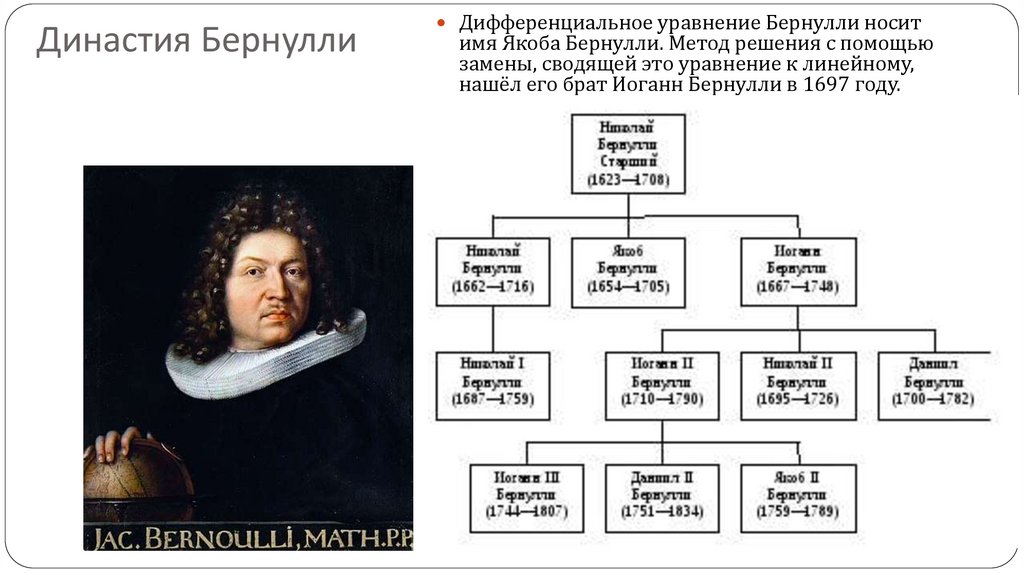
Династия Бернулли
Дифференциальное уравнение Бернулли носит
имя Якоба Бернулли. Метод решения с помощью
замены, сводящей это уравнение к линейному,
нашёл его брат Иоганн Бернулли в 1697 году.

14.

Пример.

15.

УРАВНЕНИЯ, ЛИНЕЙНЫЕ ОТНОСИТЕЛЬНО x

16.

Линейное относительно х уравнение.

17.

Приложение.
Динамическая модель
Кейнса.

18.

Приложение.
Продолжение.

19.

Приложение. Окончание.

20.

Проверка знаний
12. Какие еще методы решения линейного ДУ 1 порядка Вы
знаете?
14. Какое дифференциальное уравнение называется уравнением
Бернулли?

21.

Литература
Лутковская Е.А. 8 лекций по дифференциальным и разностным
уравнениям: учеб. пособие