Similar presentations:
Решение задач
1.
08.11.2023Классная
р а б о т а.
Решение задач.
2.
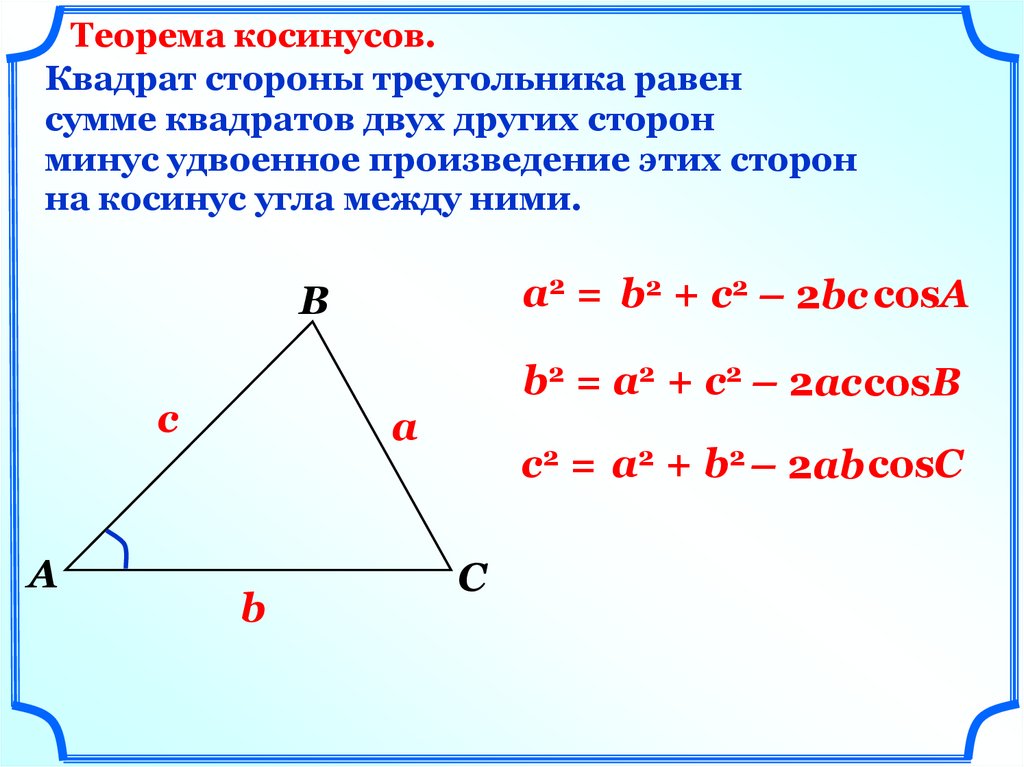
Теорема косинусов.Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих сторон
на косинус угла между ними.
a2 = b2 + c2 – 2bc cosA
B
c
A
b2 = a2 + c2 – 2accosB
a
b
c2 = a2 + b2 – 2ab cosC
C
3.
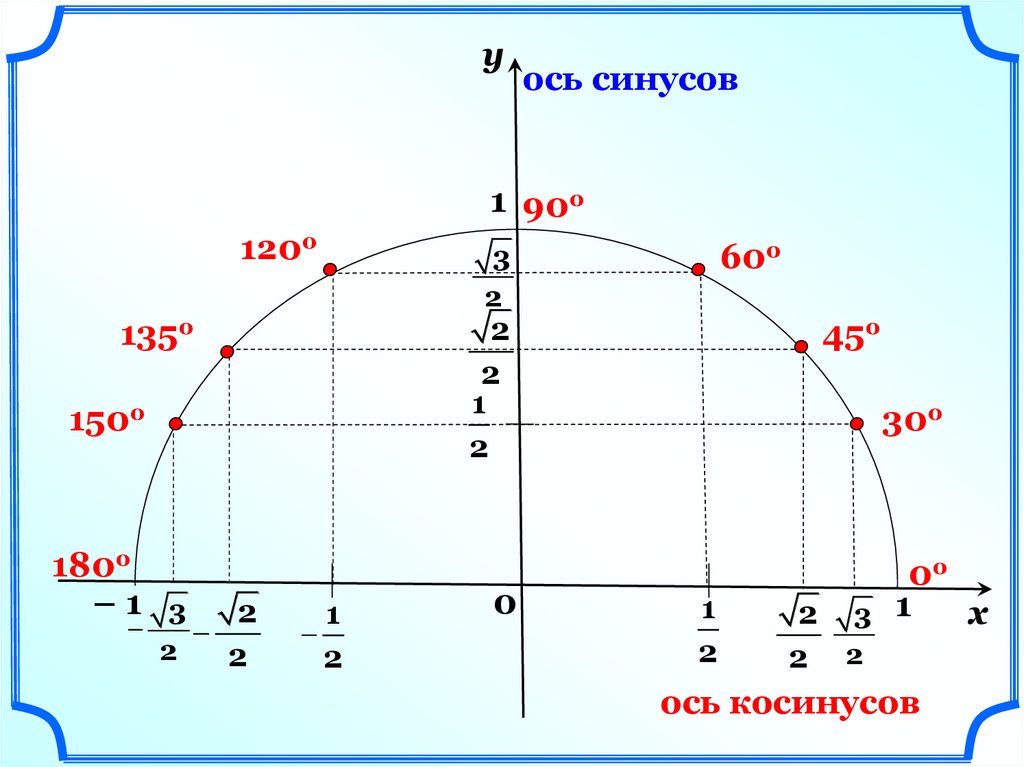
уось синусов
1 900
1200
2
2
1
2
1350
1500
1800
–1 3
2
2
2
600
3
2
1
2
0
450
300
1
2
00
3 1
х
2
2 2
ось косинусов
4.
BC
135о
ВD2 = 7 2 +(6 2)2 2 7 6 2 соs45о
7
ВD2 = 49+ 36 2 2 7 6
45о
A
1) Рассмотрим ΔАВD:
6 2
D
ВD2 = 49 + 72 – 84
ВD2 = 37
ВD = 37 см
2) Рассмотрим ΔАВС: АС2 = 49 + 72 + 84
АС2 = 205
АС = 205 см
Ответ:
37 см;
205 см.
2
2
2
5.
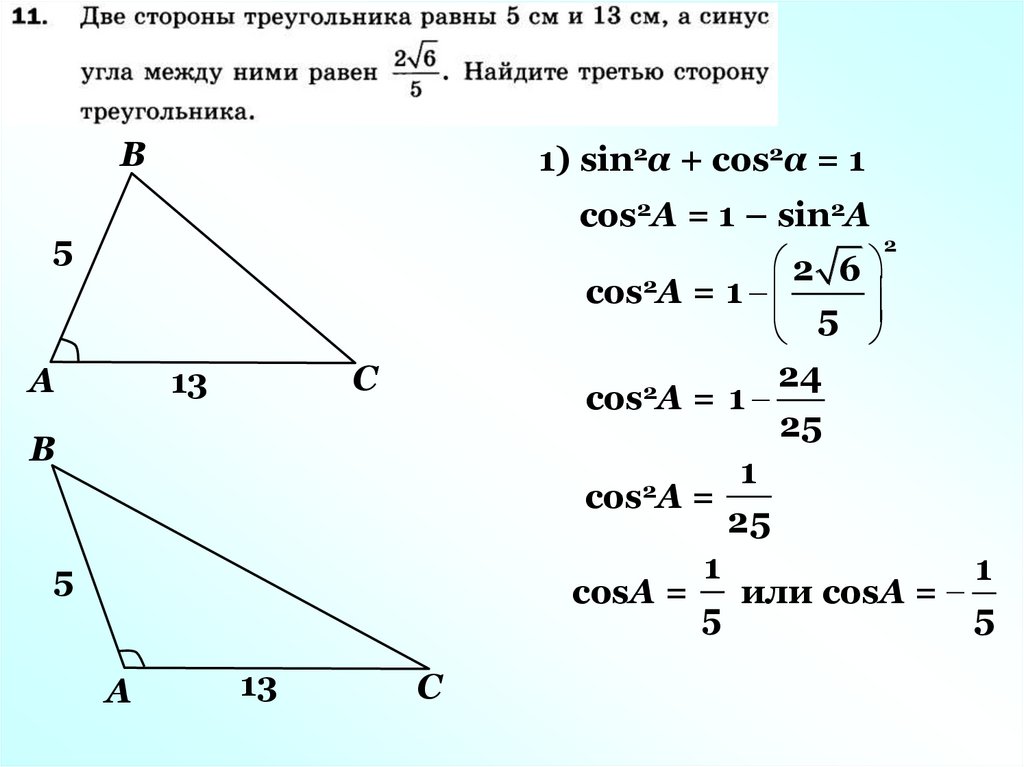
В1) sin2α + соs2α = 1
соs2А = 1 – sin2А
2
2 6
2
соs А = 1
5
24
соs2А = 1
25
1
2
соs А =
25
1
1
соsА =
или соsА =
5
5
5
А
С
13
В
5
А
13
С
6.
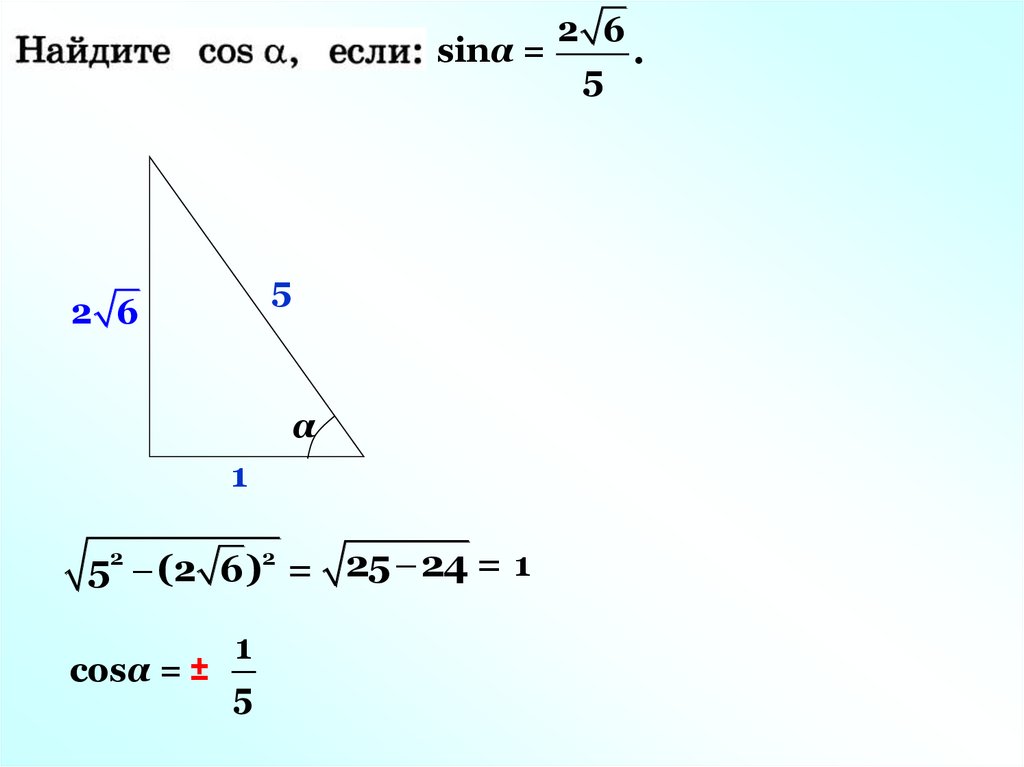
2 6sinα =
.
5
5
2 6
α
1
52 (2 6)2 = 25 24 = 1
1
соsα = ±
5
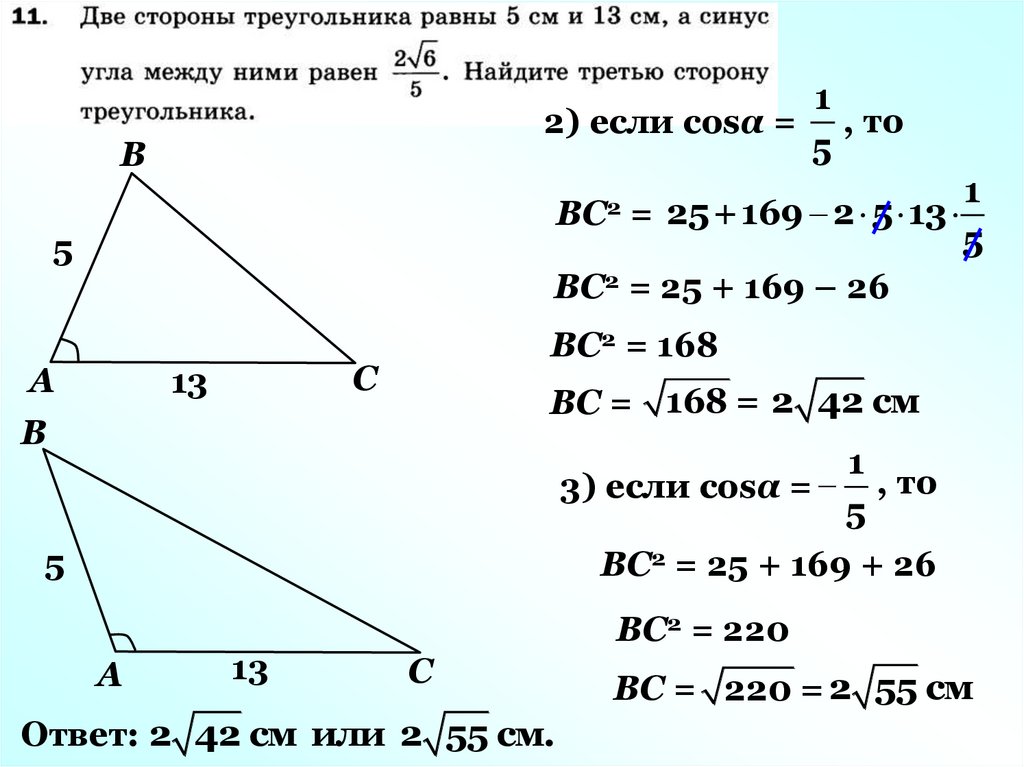
7.
12) если cosα = , то
5
В
ВС2 = 25+169 2 5 13
5
1
5
ВС2 = 25 + 169 – 26
А
ВС2 = 168
С
13
ВС = 168 = 2 42 см
В
1
3) если cosα = , то
5
ВС2 = 25 + 169 + 26
5
А
13
ВС2 = 220
С
Ответ: 2 42 см или 2 55 см.
ВС = 220 = 2 55 см
8.
Ву
1) Т.к. тч. О – центр вписанной окр.,
то АО и ВО – бис-сы углов А и В.
2) ∠А + ∠В = 180о – 120о = 60о
2
Оо 3 3
120
С
х
А
3) 2х + 2у = 60о
х + у = 30о
∠АОВ = 180о – 30о = 150о
4) Рассмотрим ΔАОВ:
АВ2 = 22 +(3 3)2 2 2 3 3 соs150о
3
2
АВ = 4 +27 2 6 3
2
АВ2 = 4 + 27 + 18
Ответ: 7 см.
АВ2 = 49
АВ = 7 см
9.
1) ВС2 = (7х)2 + (8х)2 – 2·7х·8х·соs120оВ
1
2
2
2
2
ВС2 = 49 х +64 х 2 56 х
7х
ВС2 = 169х2
120о
А
8х
ВС = 13х
С
2) 7х + 8х + 13х = 84
3) АВ = 7х = 21 см
АС = 8х = 24 см
ВС = 13х = 39 см
Ответ: 21 см, 24 см, 39 см.
28х = 84
х=3
10.
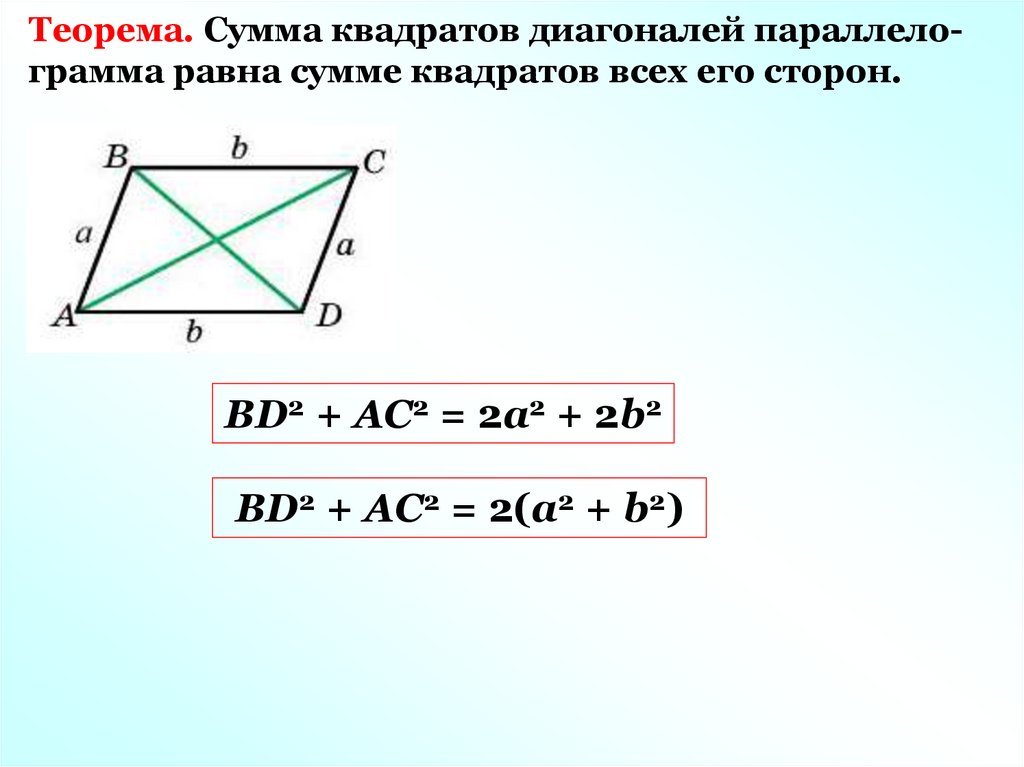
Теорема. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.BD2 + AC2 = 2а2 + 2b2
BD2 + AC2 = 2(а2 + b2)
11.
30B
15
A
9х
C
(9х)2 + (13х)2 = 2 · (152 + 302)
13х
81х2 + 169х2 = 2 · 152 · (12 + 22)
250х2 = 2 · 32 · 52 · 5 : 25
D
10х2 = 2 · 32 · 5 : 10
х2 = 3 2
х1 = 3
Ответ: 27 см, 39 см.
х2 < 0
12.
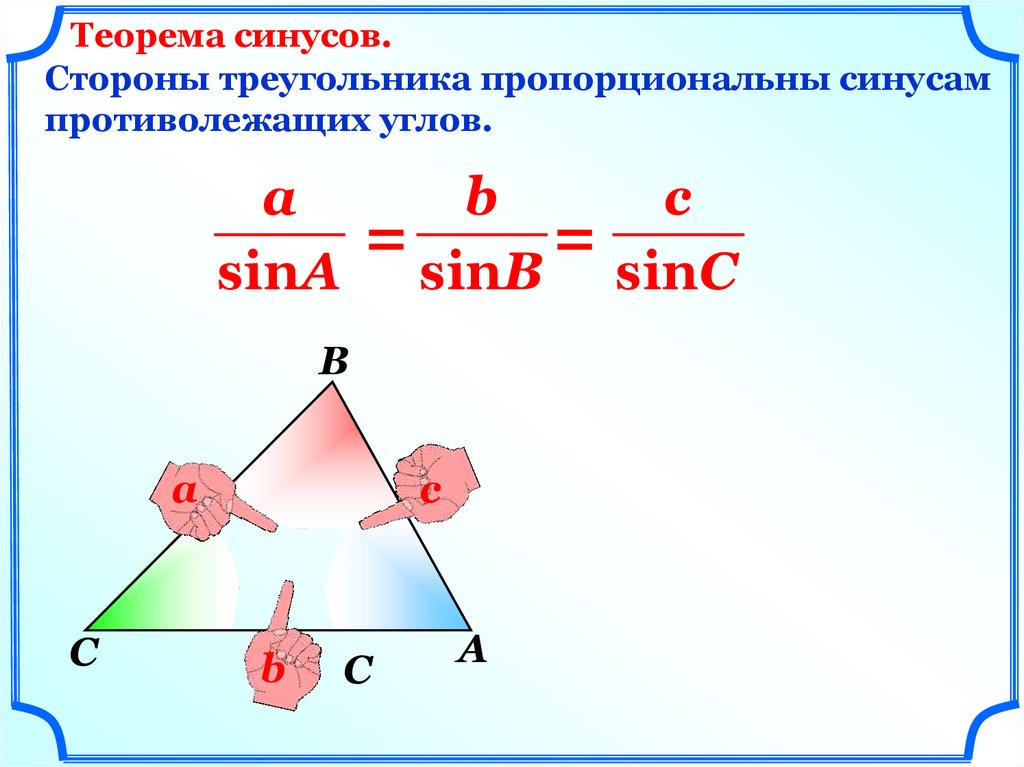
Теорема синусов.Стороны треугольника пропорциональны синусам
противолежащих углов.
а
b
с
=
=
sinА sinВ sinС
B
a
C
c
b
C
A
13.
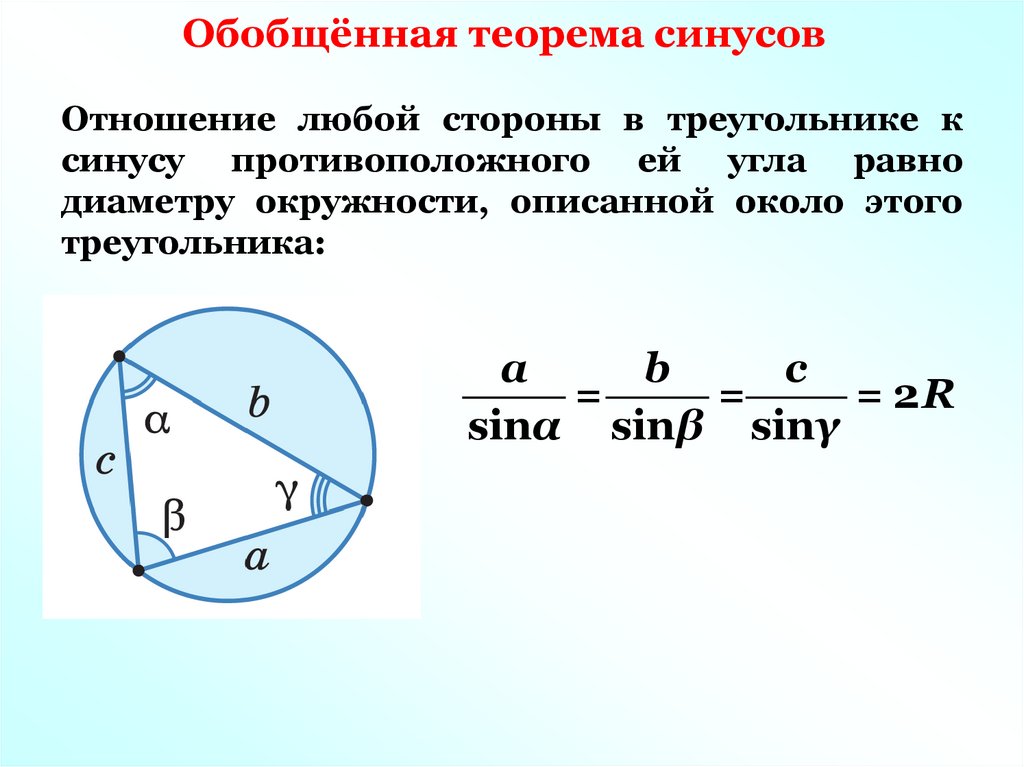
Обобщённая теорема синусовОтношение любой стороны в треугольнике к
синусу противоположного ей угла равно
диаметру окружности, описанной около этого
треугольника:
а
b
с
=
=
= 2R
sinα sinβ sinγ
14.
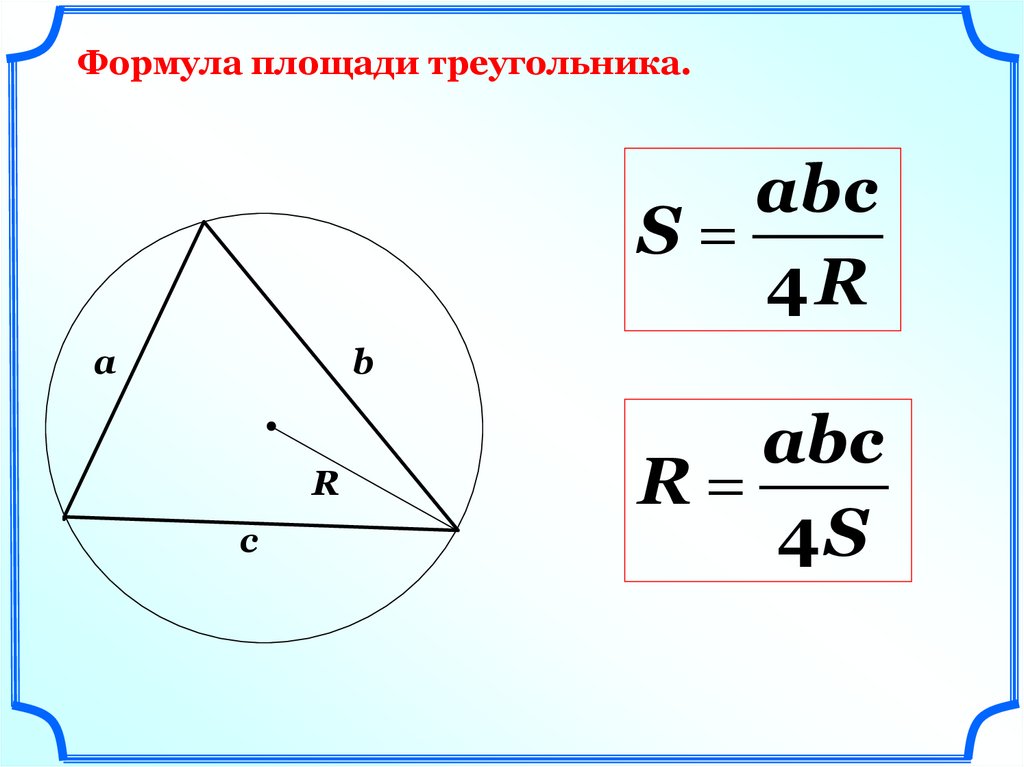
Формула площади треугольника.abc
S
4R
а
b
R
c
abc
R
4S
15.
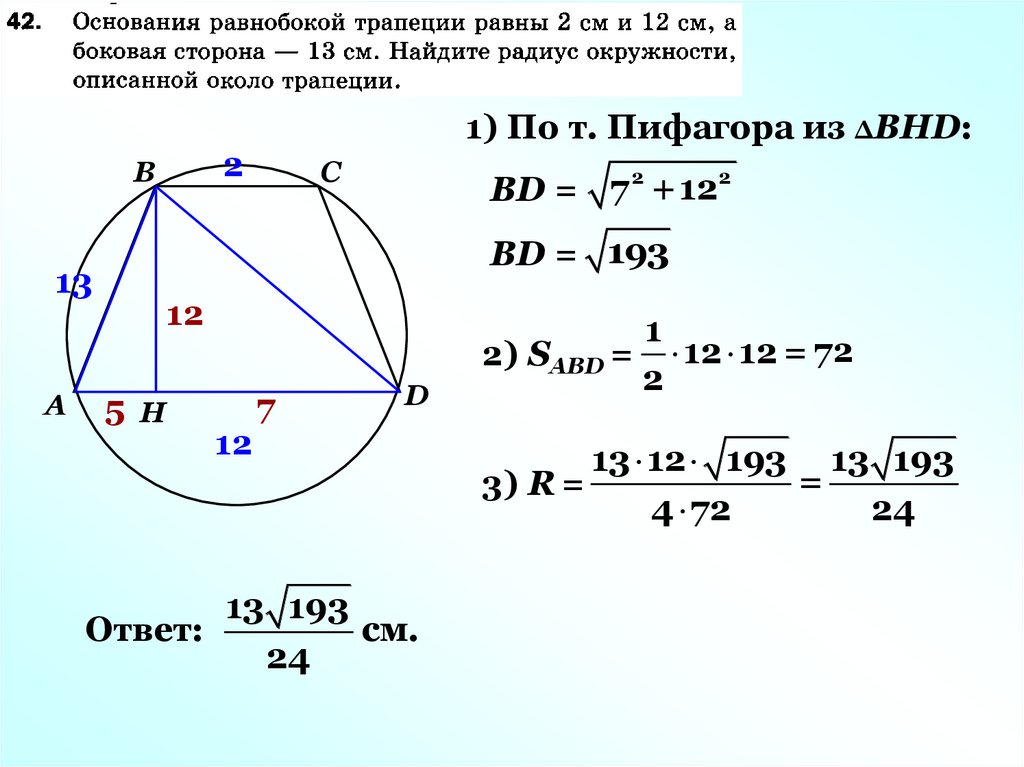
2В
С
ВD = 7 2 +122
ВD = 193
13
А
1) По т. Пифагора из ΔВНD:
12
5 Н
12
7
D
13 193
Ответ:
см.
24
1
2) SABD = 12 12 = 72
2
13 12 193 13 193
=
3) R =
4 72
24
16.
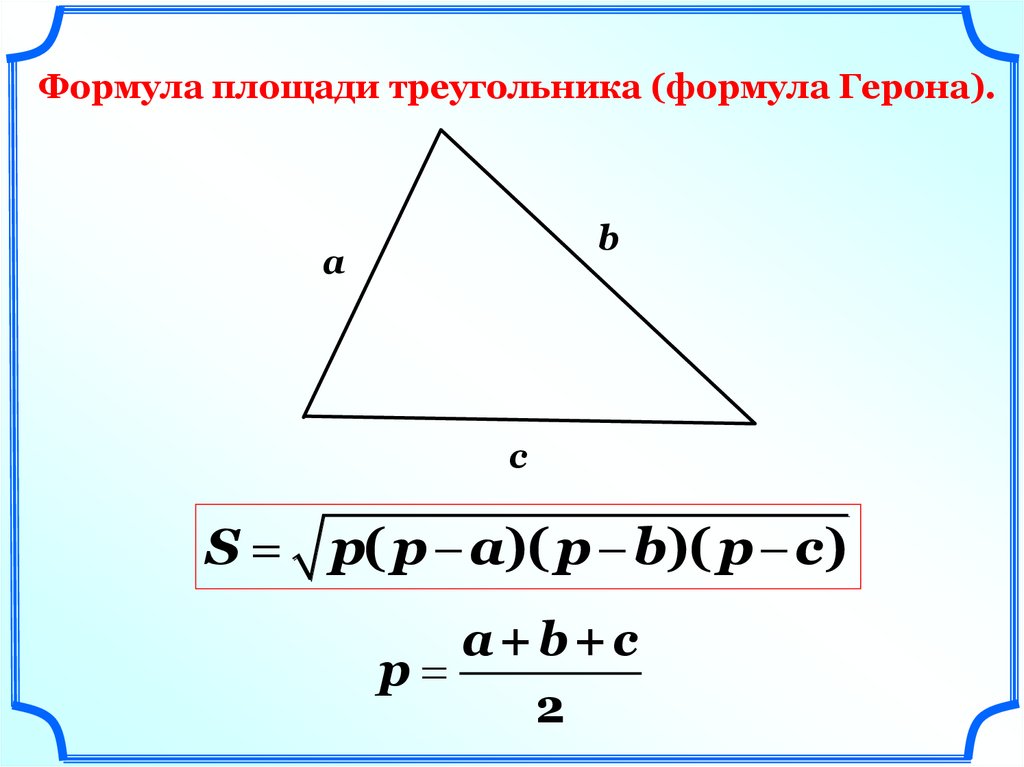
Формула площади треугольника (формула Герона).b
а
c
S p( p a)( p b)( p c)
a +b + c
p
2
17.
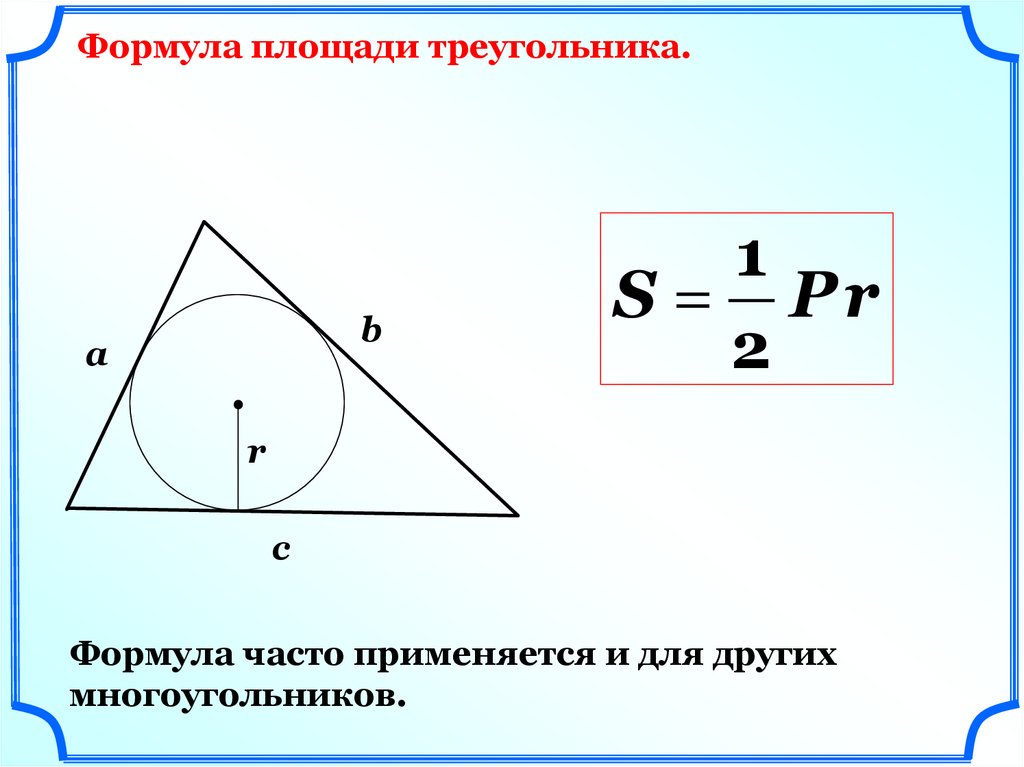
Формула площади треугольника.b
а
1
S Pr
2
r
c
Формула часто применяется и для других
многоугольников.
18.
В11
А
1) S = 22 11 9 2 =
13
= 11 · 3 · 2 = 66
h
Н 20
3) 66 = 22r
r = 3 см
С
1
2) 66 = h 20
2
10h = 66
h = 6,6 см
5
11 13 20 65
= 10 cм
=
4) R =
6
6
4 66
5
Ответ: 6,6 см; 3 см; 10 cм.
6
112 9 22 =







 mathematics
mathematics








