Similar presentations:
Растворы. Термодинамическая теория растворов
1. Растворы
Термодинамическаятеория растворов
2. Теории растворов
Корпускулярнаятеория
(18
век).
Раствор
рассматривается
как
механическая
смесь
компонентов. Частицы растворенного вещества
проникают в поры растворителя и наоборот.
Физическая теория (19 век, Оствальд, Вант-Гофф,
Аррениус). Растворитель рассматривается как
инертная
среда,
в
которой
равномерно
распределены молекулы растворенного вещества.
Межмолекулярные взаимодействия отсутствуют
(аналогично модели идеального газа). Применима
только для разбавленных растворов.
3.
Химическая теория (19 век, Менделеев). Растворение –разновидность химического взаимодействия между
частицами растворителя и растворенных веществ,
сопровождающееся образованием нестойких соединений
переменного состава - сольватов (гидратов).
Современные
теории
растворов
рассматривают
образование раствора как самопроизвольный физикохимический процесс.
Термодинамическая теория растворов устанавливает
зависимость равновесных свойств растворов от состава и
свойств образующих их компонентов, не принимая во
внимание природу межмолекулярных взаимодействий и
молекулярную структуру растворов.
4. Общая характеристика растворов.
Раствор – термодинамически устойчивая гомогеннаясистема переменного состава, состоящая из двух или
более компонентов и продуктов их взаимодействия.
От химических соединений растворы отличаются
непостоянством состава и отсутствием кратных
отношений.
С позиций ХТД все компоненты раствора
равноценны, и деление на растворитель и
растворенные вещества условно.
Растворитель – компонент раствора, взятый в
избытке и находящийся в том же агрегатном
состоянии, что и раствор.
5. Классификация растворов
1. По агрегатному состоянию: газообразные, жидкие, твердые.2. По термодинамическим свойствам: идеальные и неидеальные
(реальные).
Идеальным называют раствор, в котором взаимодействия между
всеми частицами одинаковы независимо от их природы.
- образование идеального раствора происходит без изменения объема
∆VСМ = 0;
- не сопровождается тепловым эффектом ∆НСМ = 0;
- изменение энтропии при образовании идеального раствора не
зависит от химической природы компонентов, а является функцией
состава раствора ∆SСМ = ∆SСМ идеальных газов;
- изменение химического потенциала i – того компонента раствора
0
i
i
i СМ
RT ln x .
i
Растворы, для которых не выполняется хотя бы одно из
перечисленных условий, называют неидеальными или реальными.
6.
3. По концентрации: разбавленные, концентрированные, насыщенные,пересыщенные.
Массовая доля ωi – отношение массы данного
компонента раствора к массе раствора
(gi – количество i-того вещества, г)
Массовое
содержание
ωi
(процентная
концентрация) – масса растворенного i-того
вещества (г) в 100 г раствора
Мольная доля хi – число молей растворенного
вещества ni в 1 моле раствора
gi
wi
gi
i
wi
gi
100%
gi
i
ni
xi
ni
i
Молярность Сi– количество i-того компонента (в
молях) в 1л раствора
ni
Ci
V
Моляльность mi – количество i-того компонента (в
молях) в 1000 г растворителя
ni
mi
1000
g1
7. Парциальные мольные величины (ПМВ)
ПАРЦИАЛЬНЫЕ МОЛЬНЫЕВЕЛИЧИНЫ (ПМВ)
8.
Раствор образован двумя или болеекомпонентами, поэтому все его свойства
являются экстенсивными и относятся к
раствору как к единой термодинамической
системе.
Вклад данного компонента в общее
экстенсивное
свойство
раствора
определяется его парциальной мольной
величиной.
9.
Парциальная мольная величина отражаетизменение
какого-либо
экстенсивного
свойства раствора при добавлении к нему 1
моля
i-того компонента в условиях
постоянства Р,Т и состава раствора.
ПМВ есть частная производная от любой
экстенсивной переменной Ф по количеству
молей i-того компонента при постоянных
Р, Т и числе молей остальных компонентов
системы кроме i-того:
Ф
Фi
n
i P,T ,n j i
10.
VVi
n
i P ,T ,n j i
C
p
C
n
рi
i P ,T ,n j i
Н
Нi
n
i P ,T ,n j i
U
Ui
n
i P ,T ,n j i
Si
Fi
Gi
S
n
i P ,T ,n j i
F
n
i P ,T ,n j i
G
n
i P ,T ,n j i
i
Химический потенциал есть
парциальная мольная энергия
Гиббса компонента системы.
11. Свойства ПМВ
1) Экстенсивное свойство раствора складывается изсоответствующих ПМВ компонентов с учетом состава раствора
(свойство аддитивности):
Ф ni Фi
Ф n1 Ф1 n2 Ф2
Ф x1Ф1 x2 Ф2
0
m
Ф
Фm
n1 n2
i
- мольная величина, т. е. свойство
одного моля раствора
12.
2) Изменение ПМВ выражается как частная производная отизменения соответствующей термодинамической
переменной:
Фi
Ф
n
i P ,T ,n j i
3) Для ПМВ справедливы все соотношения, характерные
для соответствующих термодинамических функций.
Gi H i T S i
dGi Vi dP S i dT
Gi
Gi
Vi ,
Si
P T
T P
13. ПМВ первого и второго рода
ПМВ I рода в идеальных растворах любых концентрацийравны соответствующим мольным величинам чистых
компонентов в том же агрегатном состоянии, что и раствор
0
( Vi , H i , U i ).
Фi Ф m
Ф ni Фi niФm
0
i
i
ПМВ II рода зависят от концентрации раствора и не равны
мольным величинам компонентов ( S i , Gi , Fi ).
Фi Фm
0
14. Методы определения ПМВ
Аналитический метод – дифференцированиеаналитической зависимости Ф =f (ni) интегрального
свойства раствора от его состава по количеству молей
одного из компонентов.
Ф = f(n2) имеет вид
Ф a bn2 cn22
Ф
b 2cn2
Ф 2
n2 P ,T
Ф n 2 Ф2
Ф1
n1
Графические методы – основаны на построении
касательных к зависимости свойство раствора – состав.
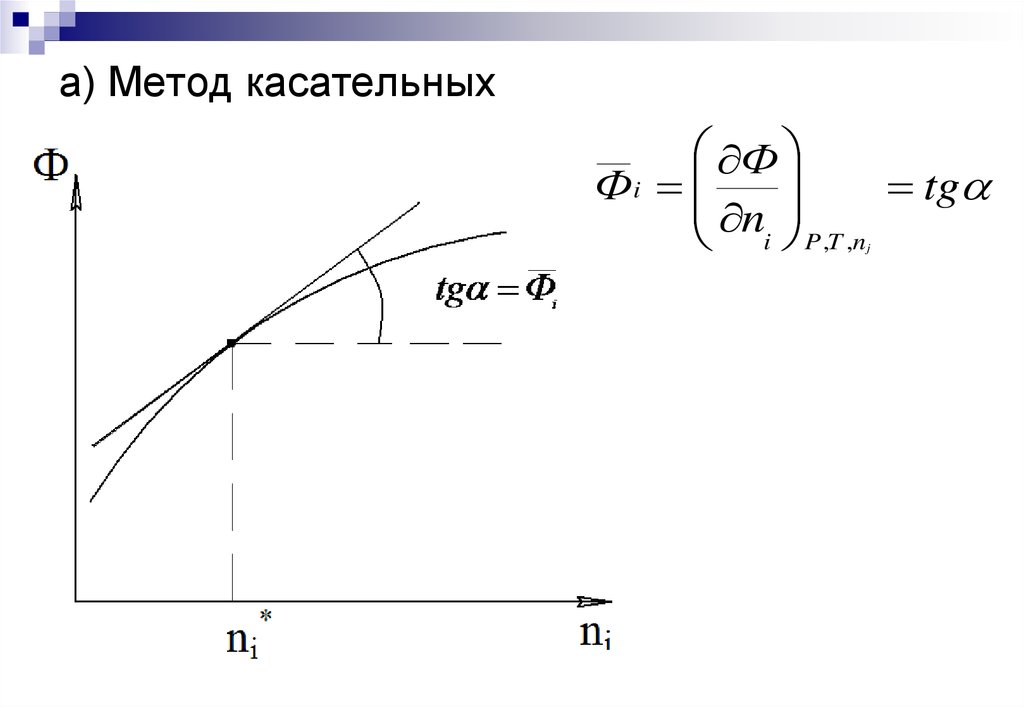
15. а) Метод касательных
ФФi
tg
n
i P ,T ,n
j
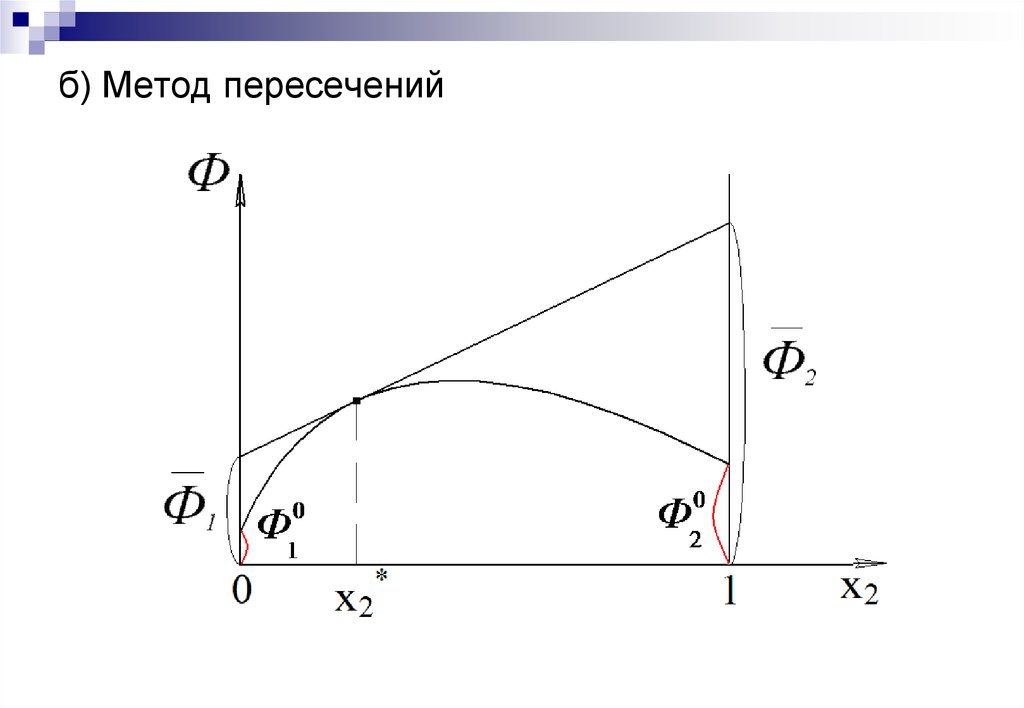
16. б) Метод пересечений
17. Парциальные мольные величины
характеризуют не само свойство, а его изменение,поэтому в отличие от мольных величин могут принимать
любые
значения
(положительные,
отрицательные,
нулевые);
парциальные мольные величины зависят от состава
раствора, поэтому при определении численного значения
ПМВ необходимо указывать состав;
парциальные мольные величины различных компонентов
раствора зависят друг от друга и связаны уравнением
Гиббса-Дюгема:
ni d Фi 0
i
18. Уравнение Гиббса-Дюгема
Образование раствора из компонентов – самопроизвольныйпроцесс при Р,Т=const, сопровождающийся уменьшением
энергии Гиббса.
dG VdP SdT dn
i
i
(1)
i
при P, T const : dG dn
(2)
G ini
(3)
i
i
i
i
dG i dni ni d i
i
(2) = (4) →
(4)
i
ni d i 0
i
(5) – уравнение Гиббса-Дюгема в неявном виде
(5)
19.
n1d 1 n2 d 2 0(6)
1 растворитель; 2 растворенное вещество
n1
d 2 d 1
n2
(7)
n1
n2
x1
, x2
n1 n2
n1 n2
x1
d 2 d 1
x2
(8)
(7) и (8) – уравнения Гиббса-Дюгема в явном виде.
Уравнения (5), (7), (8) справедливы для всех ПМВ.
20.
i i0 RT ln Pi(9)
d i RTd ln Pi
(10)
(10) → (8) :
x1
RTd ln P2 RTd ln P1
x2
x1
d ln P2 d ln P1
x2
(11) – уравнение Дюгема-Маргулиса
(11)


















 chemistry
chemistry








