Признаки равенства треугольников

1.

Двадцать шестое октября
Классная работа
Признаки равенства треугольников

2.

Повторим
Первый признак
А
Теорема:
Если две стороны и угол между
ними одного треугольника
соответственно равны двум
сторонам и углу между ними
другого треугольника, то
такие треугольники равны
С
В
С₁
А₁
В₁

3.

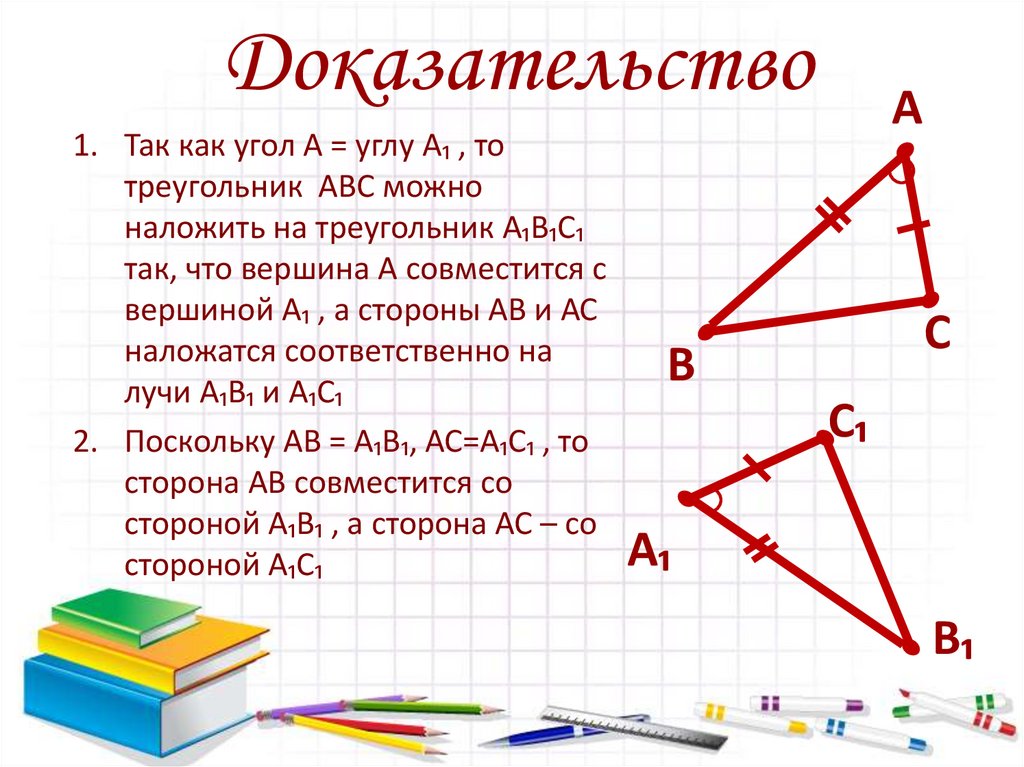
Доказательство
1. Так как угол А = углу А₁ , то
треугольник АВС можно
наложить на треугольник А₁В₁С₁
так, что вершина А совместится с
вершиной А₁ , а стороны АВ и АС
наложатся соответственно на
В
лучи А₁В₁ и А₁С₁
2. Поскольку АВ = А₁В₁, АС=А₁С₁ , то
сторона АВ совместится со
стороной А₁В₁ , а сторона АС – со
А₁
стороной А₁С₁
А
С
С₁
В₁

4.

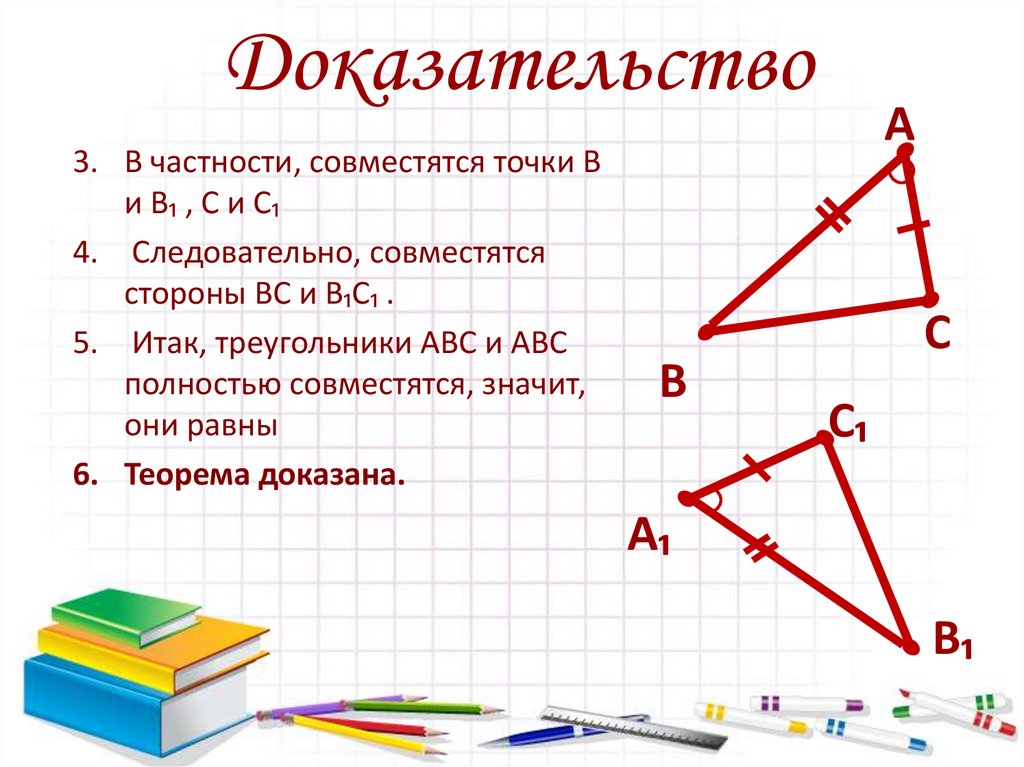
Доказательство
3. В частности, совместятся точки В
и В₁ , С и С₁
4. Следовательно, совместятся
стороны ВС и В₁С₁ .
5. Итак, треугольники АВС и АВС
полностью совместятся, значит,
они равны
6. Теорема доказана.
В
А
С
С₁
А₁
В₁

5.

Второй признак
А
Теорема:
Если сторона и два прилежащих
к ней угла одного
В
треугольника соответственно
равны стороне и двум
прилежащим к ней углам
другого треугольника, то
А₁
такие треугольники равны.
С
С₁
В₁

6.

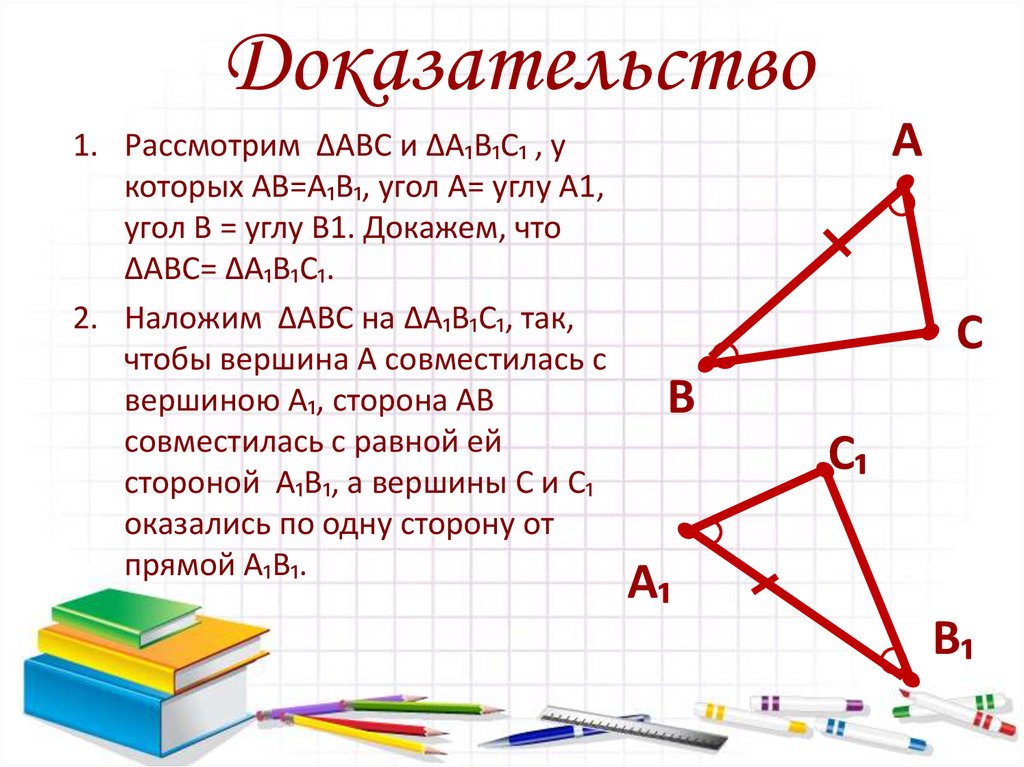
Доказательство
1. Рассмотрим ∆АВС и ∆А₁В₁С₁ , у
которых АВ=А₁В₁, угол А= углу А1,
угол В = углу В1. Докажем, что
∆АВС= ∆А₁В₁С₁.
2. Наложим ∆АВС на ∆А₁В₁С₁, так,
чтобы вершина А совместилась с
вершиною А₁, сторона АВ
совместилась с равной ей
стороной А₁В₁, а вершины С и С₁
оказались по одну сторону от
прямой А₁В₁.
А
С
В
С₁
А₁
В₁

7.

Доказательство
1. Так как угол А= углу А₁ и угол
В = углу В₁, то сторона АС
наложится на луч А₁С₁, а сторона
ВС- на луч В₁С₁.
2. Поэтому вершина С - общая точка
сторон АС и ВС - окажется
лежащей как на луче А₁С₁, так и
В
на луче В₁С₁ и, следовательно,
совместятся с общей точкой этих
лучей - вершиной С.
3. Значит совместятся стороны АС и А₁
А₁С₁, АС и В₁С₁.
Теорема доказана.
А
С
С₁
В₁

8.

Третий признак А
Теорема:
Если три стороны одного
треугольника равны
соответственно трем
сторонам другого
треугольника, то такие
треугольники равны.
С
В
С₁
А₁
В₁

9.

Доказательство А
1. Приложим ∆АВС к ∆А₁В₁С₁ так, чтобы
вершины А совместилась с А₁, В с В₁, а
С и С₁ оказались по разные стороны от
прямой А₁В₁.
2. Так как АС и А₁С₁, ВС и В₁С₁ равны, то
треугольники А₁С₁С и В₁С₁С –
1
С
В
равнобедренные. Следовательно,
3
угол 1 = 2, а угол 3 = 4
3. Поэтому угол АСВ = А₁С₁В₁.
4. Итак, АС = А₁С₁ , ВС = В₁С₁ , угол С =
А₁
углу С₁
5.
Треугольники АВС И АВС равны по
первому признаку равенства
Теорема доказана
А₁(А)
С 2
С₁
4
B₁(B)
В₁
С₁

10.

Задача № 1
D
А
C
B
Дано:
АВСD – квадрат
Докажите, что
∆АВD = ∆BCD

11.

Доказательство
• Рассмотрим ▲ABD, ▲BCD. AD =CB
=AB=CD (т.к. ABCD квадрат), BD –общая.
Следовательно ▲ABD = ▲BCD по 3
признаку, ч.т.д.

12.

Задача № 2
E
B
А
C
D
Дано:
AB = AC, < АСЕ
= < ABD
Доказать :
∆АСЕ = ∆ABD

13.

Доказательство
• Рассмотрим ∆АСЕ , ∆ABD. АВ =АС, < АСЕ =
< ABD (по условию), <А –общий,
следовательно ∆АСЕ = ∆ABD по 2 признаку,
ч. т. д.

14.

Задача № 3
C
E
А
D
B
Дано:
Отрезки BЕ и AC
точкой D делятся
пополам.
Доказать : < AED=
< CBD

15.

Доказательство
• Выполним дополнительное построение,
проведём отрезки СВ и АЕ. В
▲AED,▲CBD, ED=DB, AD=DC (по
условию), <EDA = <BDC (как
вертикальные). Следовательно ▲AED
=▲CBD по 1 признаку, ч.т.д.

16.

Домашнее задание
Выучить теоремы